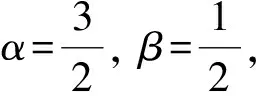带积分边值条件的分数阶微分方程解的存在性

杨 帅, 张淑琴, 王利平

(1. 中国矿业大学(北京) 力学与建筑工程学院, 北京 100083; 2. 中国矿业大学(北京) 理学院, 北京 100083)

0 引 言

目前, 分数阶微分方程在带有记忆和遗传特性的各类分子物理、 电化学、 黏弹性力学、 随机控制、 信号传输和核反应堆等领域应用广泛, 较经典的整数阶微积分更精确和灵活[1-5].

分数阶导数是一个非局部算子, 使得其在模拟实际问题中的非局部现象时具有较大优势[6-12]. Dong等[6]考虑如下非局部问题:

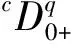
本文考虑如下Caputo分数阶微分方程边值问题:

(1)

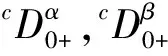
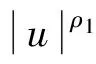
(H2) |f(t,u1,v1)-f(t,u2,v2)|≤k(|u1-u2|+|v1-v2|),k>0.

1 预备知识

设J=[0,1],C[J,]为连续函数空间,L1[J,]为一次可积空间, 定义空间

X={u(t)|u(t)∈C[J,],[J,]},

赋予范数

X在此范数下构成一个Banach空间[8], 其中0<β≤1.

定义1[1]∀α∈+, 函数f(t)的α阶Riemann-Liouville分数阶积分定义为

定义2[1]∀α∈+, 函数f(t)的α阶Caputo分数阶导数定义为

引理1[1]设α>0,f∈C[J,]∩L1[J,], 则Caputo分数阶微分方程有解

f(t)=c0+c1t+c2t2+…+cn-1tn-1,

其中ci∈,i=0,1,…,n-1,n=[α]+1.

引理2[1]设α>0,f∈C[J,]∩L1[J,], 且[J,], 则有

其中ci∈,i=0,1,…,n-1,n=[α]+1.

引理3设1<α≤2, 0<β≤1,w∈C[J,], 则Caputo分数阶微分方程边值问题

(2)

等价于积分方程

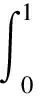
(3)

其中

(4)

证明： 设u(t)是边值问题(2)的解. 在式(2)两边作用分数阶积分算子, 由引理2可得

(5)

代入边值条件可得u(0)=c0=0. 此外, 有

代入边值条件可得

即

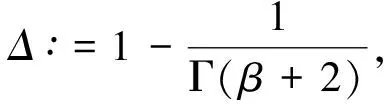
将c0,c1代入式(5), 即可得式(3)和式(4).

反之, 若u(t)为积分方程(3)的解, 则由Caputo分数阶导数的定义及性质, 易证u(t)满足边值问题(2). 因此边值问题(2)与积分方程(3)等价.

2 主要结果

定理1设1<α≤2, 0<β≤1, 若f:J××→连续, 满足条件(H1), 则Caputo分数阶边值问题(1)至少存在一个解.

证明： 由引理3, 可得Caputo分数阶微分方程边值问题(1)等价于积分方程

(6)

其中G(t,s)由式(4)给定. 在Banach空间

上定义如下算子T:

(7)

显然算子T的不动点即为Caputo分数阶边值问题(1)的解, 即将求解问题(1)转化为求解算子方程(7)的不动点问题.

首先, 给出如下估计:

则有

此外, 有

令

U={u∈X: ‖u‖X≤R},

其中

显然U是X一个非空的有界闭凸子集. 下面分两步证明.

1) 证明T:U→U.

对于任意的u(t)∈U, 根据条件(H1)有

此外, 还有

因此

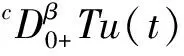
2) 证明算子T全连续.

由1)知, 算子T在U中的连续性和一致有界性显然, 因此只需证T(U)的等度连续性. 在U中, 令

对任意的u∈U,t,τ∈J, 不妨设τ

此外, 有

当t→τ时, 式(8)和式(9)右端趋于0, 则T(U)等度连续. 由Arzela-Ascoli定理知算子T全连续.

综合1),2), 由Schauder不动点定理知, 算子T在U中至少存在一个不动点, 即Caputo分数阶微分方程边值问题(1)至少存在一个解.

定理2若f:J××→连续, 满足条件(H2), 且ω=max{kΛ1,kΛ2}≤1, 其中Λ1和Λ2由定理1证明中的估计给定, 则Caputo分数阶边值问题(1)存在唯一解.

证明： 仍在Banach空间X上定义如式(7)的算子T, 由G(t,s)及f的连续性知, 算子T在X上定义合理. 下面证明T是一个压缩算子. 对于任意的u,v∈X, 由条件(H2), 可得

此外, 有

于是, 由式(10)和式(11)可得

即T是一个压缩算子.

综上, 由Banach压缩映像原理可知,T有唯一的不动点, 即Caputo分数阶微分方程边值问题(1)存在唯一的解.

3 应用实例

例1考虑如下Caputo分数阶微分方程边值问题:

(12)

则ω=kΛ2=0.419 0<1. 由定理2可知, 边值问题(12)存在唯一解.

例2考虑如下Caputo分数阶微分方程边值问题:

(13)

事实上, 可以考虑如下更一般的一类Caputo分数阶微分方程边值问题:

(14)

其中: 1<α≤2; 0<β≤1;ρ1,ρ2≥1;k1,k2>0. 由定理1可知, 边值问题(14)至少存在一个解.

[1] Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations [M]. Amsterdam: Elsevier, 2006.

[2] Diethelm K. The Analysis of Fractional Differential Equations [M]. Berlin: Springer, 2010.

[3] ZHOU Yong. Basic Theory of Fractional Differential Equations [M]. London: World Scientific, 2014.

[4] Ray S S. Fractional Calculus with Applications for Nuclear Reactor Dynamics [M]. Boca Raton, FL: CRC Press, 2015.

[5] Sabatier J, Agrawal O P, Machado J A T. Advances in Fractional Calculus [M]. Dordrecht: Springer, 2007.

[6] DONG Xiaowang, WANG Jinrong, ZHOU Yong. On Nonlocal Problems for Fractional Differential Equations in Banach Spaces [J]. Opuscula Mathematica, 2011, 31(3): 341-357.

[7] Benchohra M, Hamani S, Ntouyas S K. Boundary Value Problems for Differential Equations with Fractional Order and Nonlocal Conditions [J]. Nonlinear Analysis: Theory, Methods & Applications, 2009, 71(7): 2391-2396.

[8] SU Xinwei. Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations [J]. Applied Mathematics Letters, 2009, 22(1): 64-69.

[9] YANG Shuai, ZHANG Shuqin. Impulsive Boundary Value Problem for a Fractional Differential Equation [J/OL]. Boundary Value Problems, 2016-11-17. doi: 10.1186/s13661-016-0711-7.

[10] 代群, 王长佳, 李辉来. 用变分迭代法解分数阶微分方程组 [J]. 吉林大学学报(理学版), 2014, 52(5): 901-905. (DAI Qun, WANG Changjia, LI Huilai. Solving Systems of Fractional Differential Equations by Variational Iteration Method [J]. Journal of Jilin University (Science Edition), 2014, 52(5): 901-905.)

[11] 贾秀利, 关丽红, 汤宇. 分数阶Brown运动驱动的带跳随机微分方程的随机最大值原理 [J]. 吉林大学学报(理学版), 2016, 54(3): 521-523. (JIA Xiuli, GUAN Lihong, TANG Yu. Stochastic Maximum Principle for Stochastic Differential Equations Driven by Fractional Brownian Motion with Jumps [J]. Journal of Jilin University (Science Edition), 2016, 54(3): 521-523.)

[12] 王晗, 李辉来. 一类非线性分数阶微分方程解的存在性 [J]. 吉林大学学报(理学版), 2016, 54(5): 1039-1042. (WANG Han, LI Huilai. Existence of Solutions for a Class of Nonlinear Fractional Differential Equations [J]. Journal of Jilin University (Science Edition), 2016, 54(5): 1039-1042.)