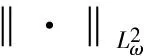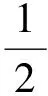求解非线性时间分数阶Klein-Gordon方程的谱配置方法
周 琴, 杨 银
(1. 湖南涉外经济学院 信息科学与工程学院, 长沙 410205; 2. 湘潭大学 数学与计算科学学院, 湖南 湘潭 411105)
1 引言与预备知识
分数阶积分微分方程在流体力学、 生物学、 等离子体物理学和金融学等领域应用广泛[1-2], 其中主要包括分数阶Klein-Gordon方程[3-4]等. 分数阶积分微分方程等非局部模型因为具有非局部算子, 使得该类方程的理论研究和数值求解非常困难, 因此求解高精度的数值解具有一定的理论意义和实用价值. 文献[5]给出了分数阶扩散方程在时间空间方向上的一阶差分形式, 并给出了稳定条件; 文献[6]利用时间-空间谱方法求解了时间分数阶扩散方程, 并利用先验误差估计推导了其方法的收敛性; 文献[7-8]用无网格方法求解了时间分数阶Sine-Gordon和Klein-Gordon方程; 文献[9]用区域分解法求解了时间分数阶Klein-Gordon方程. 谱方法是高精度的全局方法, 在保证相同精度的前提下, 谱方法比其他低阶方法所用的信息量更少, 因此高阶的谱方法更适合处理非局部方程. 文献[10-11]提出了一种新的Jacobi谱配置法来求解积分微分方程的数值解; 文献[12]利用Jacobi谱配置法求解了一类分数阶积分微分方程. 本文利用Jacobi谱配置方法数值求解如下非线性时间分数阶导数为Caputo导数的Klein-Gordon方程:
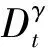
(1)
其初始条件为
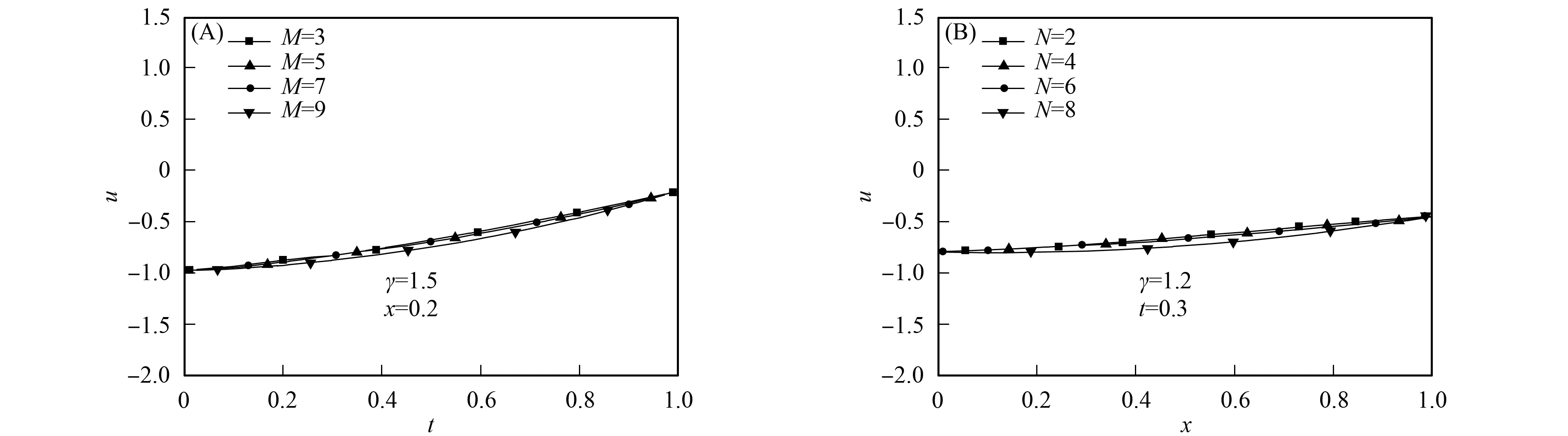
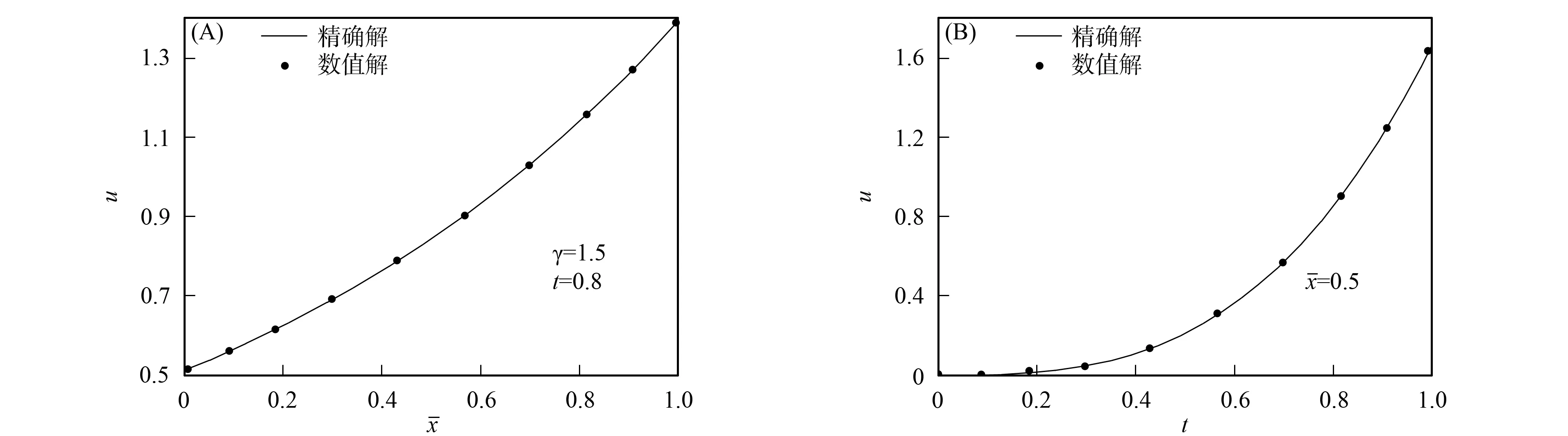
u(x,0)=φ1(x),ut(x,0)=φ2(x),a (2) 边界条件为 u(a,t)=ψ1(t),u(b,t)=ψ2(t), 0 (3) (4) 这里Γ(·)是Gamma函数. (5) 可得如下关系: (6) ωα,β(x)=(1-x)α(1+x)β (x)dx, ∀p(x)∈P2N+1, 即Jacobi-Gauss求积公式. 在方程(1)中用γ阶Riemann-Liouville分数阶积分, 并利用关系式(6), 可得如下带奇异核的积分形式方程: 其中: 为了应用正交多项式, 做如下变量变换, 使变量在标准区间[-1,1]上: 方程(7)可写为如下形式: (8) 边值条件为 (9) 其中: 首先, 对于时间方向, 在区间[-1,1]上取Jacobi权函数 (10) 要得到问题(10)的高精度解, 最大困难在于计算积分项. 为了克服该问题, 本文利用变量替换 (11) (12) 其中 下面利用Jacobi-Gauss求积公式, 求解方程(12)中的积分项近似如下: (14) (15) (16) (17) (18) 例1考虑如下分数阶Klein-Gordon方程: 初始条件为 该问题只有当γ=2时, 才有精确解 为了验证本文方法的有效性, 首先固定空间配置点为N=24, 当γ=1.5,x=0.2时, 时间配置点分别取M=3,5,7,9, 求解其数值解如图1(A)所示. 由图1(A)可见, 当M=5,7,9时, 数值解基本重合, 因此在时间方向上, 谱配置方法是收敛的. 另一方面, 固定时间配置点为M=24, 当γ=1.2,t=0.3时, 空间配置点分别取N=2,4,6,8, 求解相应的数值解如图1(B)所示. 由图1(B)可见, 当N=4,6,8时, 数值解基本重合, 表明在空间上, 本文提出的谱配置方法也是收敛的. 图1 当γ=1.5时、 固定空间x=0.2, 在时间方向上取不同配置点的数值解比较(A), 以及当γ=1.2时、 固定时间t=0.3, 在空间方向上取不同配置点的数值解比较(B)Fig.1 Comparisons of numerical solutions for different M with γ=1.5 and x=0.2 (A),and comparisons of numerical solutions for different N with γ=1.2 and t=0.3 (B) 图2 当x=0.5取不同的γ时, 例1数值解和精确解的比较Fig.2 Comparisons between numerical solutions and exact solution of example 1 for different γ with x=0.5 为了进一步验证本文方法的可靠性, 当x=0.5, 时间配置点为M=24时, 计算γ=1.25,1.5,1.75,2.0的数值解以及γ=2.0的精确解, 结果如图2所示. 由图2可见, 当γ=2.0时, 数值解与精确解吻合较好, 表明γ=1.25,1.5,1.75时的数值解是可靠的. 例2考虑如下分数阶Klein-Gordon方程: 其中 初始条件为 u(x,0)=0,ut(x,0)=0. 该问题有精确解 u(x,t)=t2cos(πx). 图3 当γ=1.5、 固定时间t=0.8(A)及固定空间时, 例2数值解和精确解的比较Fig.3 Comparisons between numerical solution and exact solution of example 2 with γ=1.5, t=0.8 (A) and γ=1.5, =0.5 (B) (N,M)γ=1.2L∞L2ωγ=1.8L∞L2ω(4,20)8.3623×10-32.9331×10-35.5843×10-41.4692×10-4(6,20)6.0822×10-42.1739×10-41.8221×10-54.7031×10-6(8,20)1.9164×10-57.3466×10-64.0249×10-78.9289×10-8(10,20)2.2837×10-61.4738×10-67.1986×10-83.1383×10-8(20,4)5.0665×10-21.6461×10-27.4814×10-43.4855×10-4(20,6)3.2606×10-31.2068×10-31.5992×10-56.6194×10-6(20,8)2.3968×10-40.7566×10-44.7053×10-72.7287×10-7(20,10)7.4660×10-52.7982×10-53.8017×10-71.5170×10-7 图4 随配置点增加的误差变化曲线Fig.4 Variation curves of error with increase of collection points 综上, 本文针对时间分数阶Klein-Gordon方程提出了一种时间-空间谱配置法, 使得方程对于时间和空间方向, 在Jacobi谱配置点成立, 从而得到其全离散形式, 并给出数值算例说明所求近似解很好地逼近了精确解. 该方法易于处理非线性的情形, 可以用较少的点得到较高精度的数值解, 节省存储空间且易推广到高维情形. [1] Miller K S, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations [M]. New York: Wiley, 1993. [2] Hilfer R. Applications of Fractional Calculus in Physics [M]. Singapore: World Scientific, 1999. [3] Kurulay M. Solving the Fractional Nonlinear Klein-Gordon Equation by Means of the Homotopy Analysis Method [J/OL]. Advances in Difference Equations, 2012-11-02. http://www.advancesindifferenceequations.com/content/2012/1/187. [5] CHEN Changming, Liu F, Burrage K. Finite Difference Methods and a Fourier Analysis for the Fractional Reaction-Subdiffusion Equation [J]. Applied Mathematics and Computation, 2008, 198(2): 754-769. [6] LI Xianjuan, XU Chuanju. A Space-Time Spectral Method for the Time Fractional Diffusion Equation [J]. SIAM Journal on Numerical Analysis, 2009, 47(3): 2018-2131. [7] Dehghan M, Abbaszadeh M, Mohebbi A. An Implicit RBF Meshless Approach for Solving the Time Fractional Nonlinear Sine-Gordon and Klein-Gordon Equations [J]. Engineering Analysis with Boundary Elements, 2015, 50: 412-434. [8] Dehghan M, Abbaszadeh M, Mohebbi A. The Numerical Solution of the Two-Dimensional Sinh-Gordon Equation via Three Meshless Methods [J]. Engineering Analysis with Boundary Elements, 2015, 51: 220-235. [9] Jafari H. Numerical Solution of Time-Fractional Klein-Gordon Equation by Using the Decomposition Methods [J]. Journal of Computational and Nonlinear Dynamics, 2016, 11(4): 041015. [10] YANG Yin, CHEN Yanping, HUANG Yunqing, et al. Convergence Analysis of Legendre-Collocation Methods for Nonlinear Volterra Type Integro Equations [J]. Advances in Applied Mathematics and Mechanics, 2015, 7(1): 74-88. [11] YANG Yin, CHEN Yanping. Spectral Collocation Methods for Nonlinear Volterra Integro-Differential Equations with Weakly Singular Kernels [J/OL]. Bulletin of the Malaysian Mathematical Sciences Society, 2017-03-22. doi: 10.1007/s40840-017-0487-7. [12] YANG Yin, CHEN Yanping, HUANG Yunqing. Convergence Analysis of the Jacobi Spectral-Collocation Method for Fractional Integro-Differential Equations [J]. Acta Mathematica Scientia, 2014, 34B(3): 673-690.

2 Jacobi谱配置法
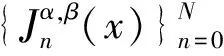
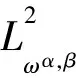

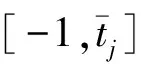

3 数值算例