中学生几何题目的分析视角演变
刘翰文
重庆市第一中学 重庆 400000
几何知识是人们在日常生活中不断发现并积累起来的一门具有实用性的数学知识,在初中、高中阶段的数学知识学习过程中,几何知识不仅内容复杂,且相关题目的难度较大,多以计算、求证类型题目为主,且平面几何与立体几何在难度上也存在着一定的差异[1]。因此,通过对几何问题的演变进行相关讨论,可以了解几何类型题目的不同变式,从而对几何知识有一个更为系统的掌握。
1 基于平面关系的几何证明题分析
在几何类型题目的实际解题过程中,我们会经常遇到一些特殊的三角形,其中,在给出部分已知条件的情况下,则需要进行特殊三角形之间关系的判定,最具有代表性的则是全等三角形的证明与应用[2]。
例1 在图1中,已知△ABC为直角三角形,且AB=AC,在这种情况下,线段AC上有一点D,连接BD,使得BD为∠ABC的平分线,延长 BD至点E,且BD⊥EC。此时,求证BD=2CE。
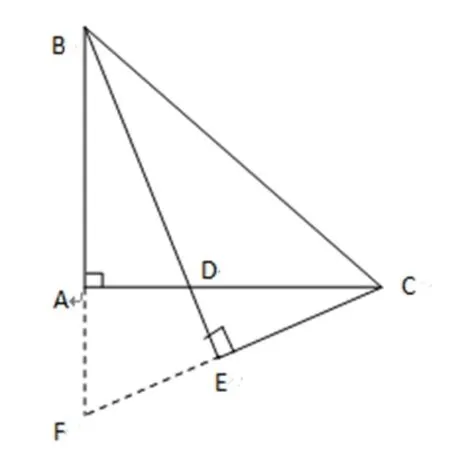
图1
解析:在分析此类题目的过程中,需要意识到平面几何图形中的相关角度关系,通常情况下,若要证明线段之间的长度关系,则多转移至对其所在三角形全等、相似进行解题。此处使用的是通过边角关系证明三角形全等,并结合特殊三角形的中垂线最终确定BD=2CE。
解:如图1所示,反向延长AB,并与CE的延长线交于一点F。
已知,△ABC为直角等腰三角形,AB=BC,且∠ABD=∠ECD=22.5°,∠ BAC=∠ FAC=90°。
根据三角形全等的判定条件,△ABD和△ACF为全等三角形(角边角)。
因此,BD=FC。
由于BE为∠FBC的平分线,且,BE⊥FC,所以,△BFC为等腰三角形,BE为△BFC的中垂线,点E为FC的中点,即CE=EF。
所以,BD=FC=2CE。
2 以几何变形为突破点的牛顿定理分析
牛顿不仅是著名的物理学家,他在众多领域都有这一定的造诣,其中就包括牛顿在几何领域提出的三大定理。在定理1中,牛顿对完全四边形的点、线关系,进行了深入分析,并通过作辅助线的方式发现了“牛顿线”的存在,具体如图2所示。

图2 牛顿第一定理的集合示意图
例2 在以ABCD围成的四边形内,AB、CD的延长线交于点E,且P、Q为BE、CE的中点,延长BC与AD交于一点F,连接EF,延长PQ并与EF交于一点N,R为BC的中点,连接PR、QR分别于BD、AC交于点M、L,所谓“牛顿线”,即M、L、N在一条直线上。
解析:在四边形ABCD中,由于点L在线段RQ上,因此QL*AB=EA*LR,且点M、R、P同样在一条直线上,因此,同理存在RM*DE=CD*MP;如此可以继续获得N、P、Q三点在一条直线上,且满足PN*FC=BF*NQ。
在此情况下,则将三个等式左右两边同时相乘,可得到如下结果:
(QL*AB)*(RM*DE)*(PN*FC)=(EA*LR)*(CD*MP)*(BF*NQ)①
基于梅涅劳斯定理,存在AB*DE*FC=EA*CD*BF,对式①变形后可得:QL*RM*PN=LR*MP*NQ,即QL/LR*RM/MP*PN/NQ=1。
同理,根据梅涅劳斯定理,点L、M、N分别在△QPR的QR、PR、QP上,且同时满足QL/LR*RM/MP*PN/NQ=1,因此可以判定L、M、N三在同一直线上。
3 总结
在数学的知识体系中,几何知识的变形较多,且难度较大,我们应当掌握多元化的几何题目解题方法,并通过深化解题方式,提高对不同题目类型的应对能力。除平面几何以外,关于立体几何的问题分析,还要求我们高中生具有较强的空间思维能力和逻辑分析能力,这也是现阶段高考几何题目中的考察重点。因此,在高中几何相关知识的学习过程中,应当加强在这一方面的训练,从而实现个人数学综合素养的提升。

