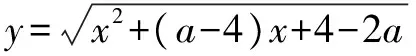如何设计循序渐进的解题教学

郑菊萍

(江苏省溧阳市光华高级中学 213300)

问题解关于x的不等式x2+(a-4)x+4-2a<0．

分析这是在一轮复习教学阶段，笔者给出的一个含参不等式问题．对于参数不等式，学生掌握得一般都不是特别理想．教学首先引导学生如何解决该问题．

师：大家尝试下，本题如何解决？

生：可以直接利用求根公式求根．

师：可以，但是这样的解决一定十分复杂，也不是考查的本意．

生：本题可以因式分解为x-2x-2-a<0，这样方便很多．

师：正确！这才是问题解决的正确途径．请同学们具体说一说解决过程．

生：将不等式分解为x-2x-2-a<0，根据一元二次不等式的解法，两根x1=2,x2=2-a的大小未定，讨论根的大小，进而解不等式．当2>2-a即a>0时，2-a

师：好．不等式对于我们来说是一种工具，学不等式主要的作用是体现在各种具体需要的问题情境中，我们来看一个变式．

设计思路：以一道基本教材课后习题为根本设计本课，让学生感受教材问题的重要性，为随后不断将问题提高难度奠定知识基础．

生：对于本题，我认为其本质是思考不等式的问题．即对任意的变量，满足不等式x2+(a-4)x+4-2a≥0恒成立，可以从函数的角度思考．

师：分析很到位，其本质还是如何解决不等式问题，请给出具体过程．

生：由题意等价为x2+(a-4)x+4-2a≥0在R上恒成立，则Δ=(a-4)2-4(4-2a)≤0，解得a=0．

设计意图：对不等式问题进行简单的包装，以函数背景为载体，让学生通过自我分析认知问题的本质依旧是解决不等式，从而理解解不等式知识对定义域求解的重要性．

上升设计2：二次函数f(x)=x2+(a-4)x+4-2a，若不等式f(x)<0的解集为A，又B=x1

师：本题如何思考？

生：我认为，这是一道以集合为载体的不等式问题．只要解决集合A，利用子集关系即可求解．

师：分析得正确.由前面的问题可知，函数f(x)=(x-2)(x-2+a)=0的两个零点x1=2、x2=2-a，只需方程的根在区间1,3内即可，转化为二次方程根的分布．但这一问题解决时候，涉及到集合中的子集，你认为特别需要考虑什么问题？

生：子集中空集的可能性．

师：正确，请给出具体过程．

生：但注意空集这特殊情况．考虑到二次函数图象开口向上，利用二次函数的图象特征，只需方程f(x)=0的根均在区间1,3内，则①A=Ø,则a=0；②A≠Ø,则2∈(1，3)，所以2-a∈1,3，则a∈-1,0∪0,1.综上所得a∈-1,1．

设计意图：本变式问题的背景依旧是同前面问题，降低了问题在课堂教学中的读题时间，提高了教学时效．进一步分析要引导学生关注不等式解决过程中，子集中空集的可能性，提高问题难度的同时，也保障思维的全面性．

上升设计3：方程log4x2+alog4x+4-2a=0在16，+∞上有两不等实根，求a的取值范围．

师：思考变式3，对于本题如何处理？

生：我认为首先需要借助换元，让问题显示得更清晰一些．用换元的思想设log4x=t，则方程就等价为t2+at+4-2a=0在t∈2,+∞有不同两解，转化为二次方程根的分布的基本题型．

师：从方程的角度思考，如何分析在t∈2,+∞有不同两解？

师：正确．将换元思想融入到问题之中，要学会从思想的视角进一步审视问题，从而理解问题的本质依旧回归到函数与方程，在解决问题过程中，如何利用不等式，这是依赖图形化的策略解决根与系数的关系．

设计意图：问题层层递进过程中，换元思想的介入是必不可少的途径，不妨进一步思考条件改为log4x改为2x，将区间改变又如何呢？这些都是换元思想作用于具体问题的体现，是教学需要渗透关注的．

上升设计4：对于任意α∈-π,π，不等式cos2α+(4-a)sinα+2a-5<0恒成立，求a的取值范围．

师：对于本题变式，如何思考？

生：我认为依旧是换元思想首先需要介入，然后寻求不等式问题的解决．

师：是的．但明显这里换元后，对变量自身的范围要思考，对恒成立处理的方式要思考．先将问题做等价的处理，请同学们说一说．

生：令cosα=x,α∈-π,π,则x∈-1,1，原题就等价于对于任意x∈-1,1 ，不等式x2+(a-4)x+4-2a>0恒成立，求a的取值范围．

师：接下来恒成立问题的处理，请同学们思考恒成立问题处理的最佳角度？

师：很好！通过解不等式，我们理解了不等式知识在各种情境问题中的作用，知识的灵活运用需要不断地熟练运用和总结．

本课是笔者解题教学中的一个小小片断，从解不等式到函数定义域、到换元思想的介入，我们发现这些类似问题都将不等式知识如何灵活运用给出了典型的示范.解题教学恰恰要这样的设计：来源于教材的问题为载体，进行加工、变式、改编、深化，让知识的整体性在不同的问题中展示出来，获得更为宽泛的运用，从而提升知识的理解是教师的重要工作．

参考文献：

[1]吴志雄.培养高中生数学应用意识的策略与思考[J].中学数学研究,2013(7).

[2]刘见乐.用思想方法指导高中数学教学[J].中国数学教育,2014(5).

[3]刘见乐.用函数思想指导高中数学解题[J].中国数学教育,2011(5).