Proper Conformal Killing Vectors in Kantowski-Sachs Metric
Tahir Hussainand Muhammad Farhan
Department of Mathematics,University of Peshawar,Khyber Pakhtunkhwa,Pakistan
1 Introduction
Let M be a spacetime with Lorentz metric g.A global smooth vector field ξ on M is called a CKV if:[1]
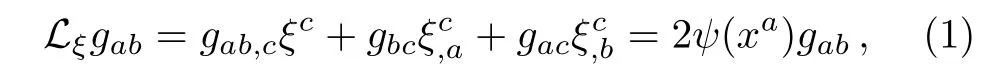
where ψ :M → R is a smooth real-valued function on M,called the conformal factor and Lξdenotes the Lie derivative operator along ξ.
The existence of a CKV is connected with the Weyl tensor by the following condition:
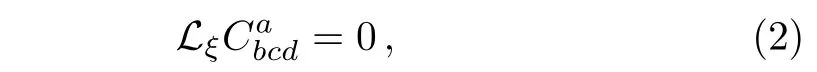
A CKV is called a homothetic vector(HV)if ψ becomes a constant and a Killing vector(KV)if ψ=0.A CKV which is not homothetic is known as proper CKV.A CKV for which ψ;mn=0,in every chart of M,is called a special conformal Killing vector.The set of all CKVs on M constitute a finite-dimensional Lie algebra under the Lie bracket operation,called conformal algebra,such that its dimension is less than or equal to 15.If M is conformally flat,it admits 15-dimensional Lie algebra of CKVs.Conversely,if the dimension of conformal algebra is 15(in fact if greater than 7),then M is conformally flat.The subsets of conformal algebra containing homothetic,Killing and special CKVs form its subalgebras,that are named as homothetic,Killing and special conformal algebras.
Conformal symmetries help to provide deeper insight at all levels of general relativity,such as geometry,kinematics and dynamics.At geometry level,the CKVs make possible the choice of coordinates so that one of the metric components is singled out and thus the metric is simplified.[2]The CKVs have the geometric property of preserving the structure of the null cone by mapping null geodesics to null geodesics.The CKVs are also helpful at kinematic level as they impose restrictions on the kinematic variables such as rotation,expansion and shear,and produce many interesting results.[3−4]At dynamics level,CKVs can be used for different purposes,the most important of which is to obtain the new exact solutions of Einstein’s field equations with better physical properties.CKVs also play a key role in the classification and categorization of the known solutions of the field equations.
In recent literature,many researchers have worked on conformal symmetries.Rahaman et al.,[5−6]studied the anisotropic and relativistic stars admitting CKVs.Esculpi and Aloma[7]worked on a charged fluid sphere with a linear equation of state admitting CKVs.The authors have also discussed the dynamical stability analysis of the system.Usmani et al.[8]studied the charged gravastar admitting CKVs.The CKVs in RobertsonWalker spacetimes are investigated by Maartens and Maharaj.[9]The same authors gave a detailed analysis of the existence of CKVs in pp-waves spacetimes.[10]Moopanar and Maharaj[11]studied the conformal geometry of spherically symmetric spacetimes without specifying the form of the matter distribution.Rigidly rotating perfect fluids admitting proper CKVs are explored by Kramer and Carot.[12]Recently,Hussain et al.presented CKVs in locally rotationally symmetric Biachi type V,static and non static plane symmetric spacetimes.[13−15]
In fluid spacetimes,a CKV need not map fluid flow lines into fluid flow lines.Such an example from a perfectfluid FRW spacetime is presented in Ref.[3].A CKV ξ is said to be inherited by the physical fluid source represented by the energy-momentum tensor if the fluid flow lines are mapped conformally into the fluid flow lines.Such CKVs are usually known as inheriting conformal Killing vectors(ICKVs)and they satisfy the relation:[16]
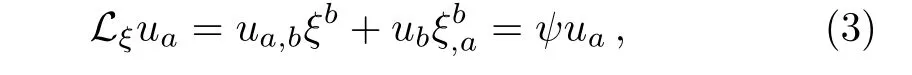
where uais the four velocity of the fluid.Like the CKVs,the ICKVs are also studied in some well known fluid spacetimes,for details we refer to Refs.[16–19].
Inspired by these early work on conformal and inheriting conformal symmetries,we are looking forward to investigate the existence of proper CKVs and ICKVs in Kantowski-Sachs metric.We organize the paper as follows:
In next section,we solve the set of coupled conformal Killing equations for Kantowski-Sachs metric and find the general form of vector field generating CKVs and the conformal factor,subject to some integrability conditions.These integrability conditions are solved in different cases to get the closed form of CKVs.Section 3 is devoted to the study of ICKVs in Kantowski-Sachs metric.A brief summary of the present work is presented in the last section.
2 Proper Conformal Killing Vectors
The Kantowski-Sachs class of metrics represent homogeneous and anisotropically expanding(contracting)cosmologies,which admit a four-parameter continuous isometry group G4acting on homogeneous spacelike hypersurfaces. In spherical polar coordinates(t,r,θ,ϕ),the Kantowski-Sachs metric can be written as:[20]

where A(t)and B(t)are non-zero functions of t only.The above metric admit a minimal set of four KVs,which are listed below:
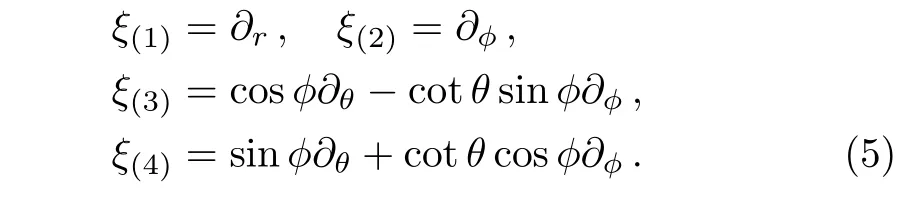
For the Kantowski-Sachs metric given in Eq.(4),the conformal Killing equation(1)gives rise to the following system of ten coupled partial differential equations,known as conformal Killing equations:

To obtain the explicit form of CKV ξ=(ξ0,ξ1,ξ2,ξ3)in Kantowski-Sachs metric,we need to solve the above system of equations.Using some simple algebra,these equations can be integrated to get the following expressions for ξaand the conformal factor ψ in terms of known functions of θ and ϕ and unknown functions of t and r:
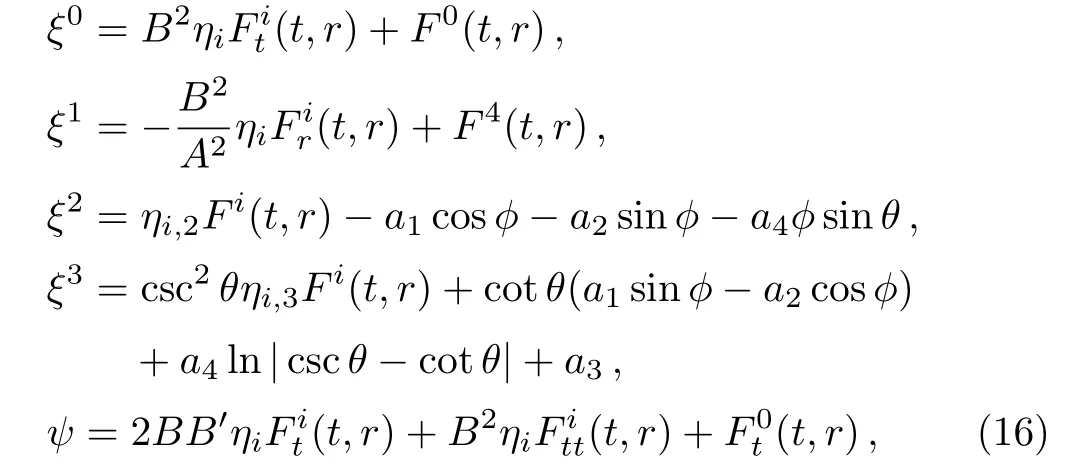
where ηi=(η1,η2,η3)=(sinθsinϕ,−sinθcosϕ,−cosθ)and Fi(t,r)are unknown functions,which arise in the process of integration.Some of the conformal Killing equations are identically satis fied by the above values of ξa,while by substituting these values in the remaining equations,we get a4=0 and the following integrability conditions are generated:
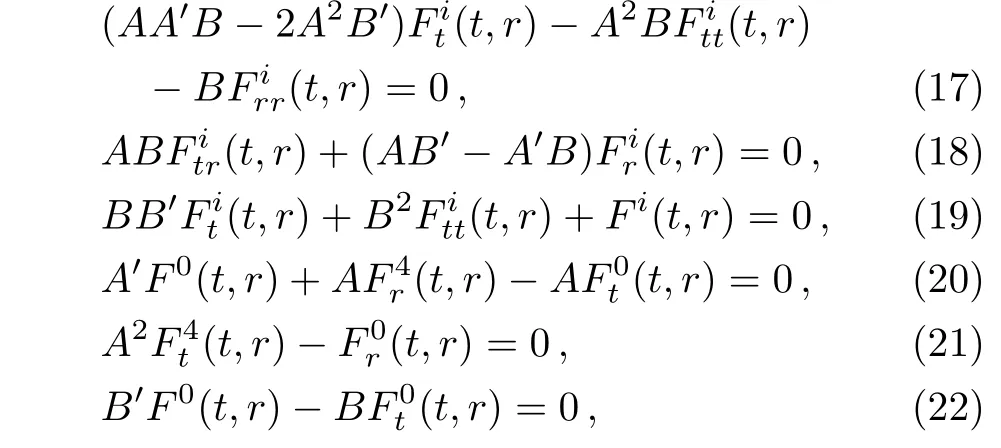
where i=1,2,3.If we could solve the above system of equations,we would get the explicit form of CKVs and the conformal factor,given in Eq.(16).Here we discuss some cases in which these equations are completely solved to get the final form of CKVs.
Case 1In this case,we consider A′≠0,B′≠0 and follow the approach of classifying the conformal symmetry in terms of the Weyl tensor.The non-zero components of the Weyl tensor for the Kantowski-Sachs metric,given in Eq.(4),are:
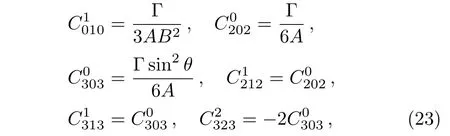
where Γ =ABB′′−AB′2−A′′B2+A′BB′−A.If Γ =0,all the components of the Weyl tensor vanish and the spacetime become conformally flat.Applying the formula given in Eq.(2)for the above Weyl tensor components,we obtain:
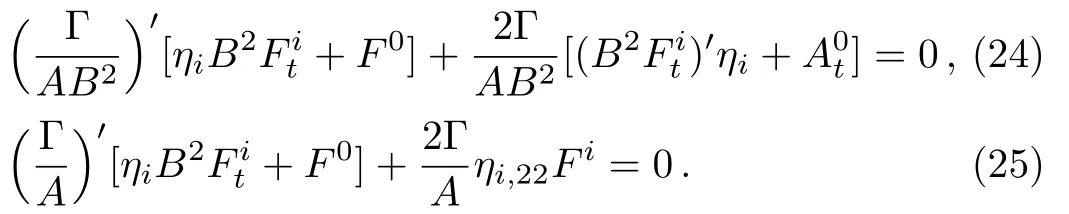
Consequently,the linear independence of the trigonometric functions in ηigives:

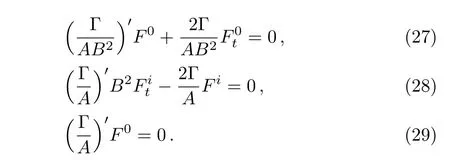
The above four equations are the necessary and sufficient conditions for the integrability conditions,Eqs.(17)–(22),to be satis fied.Here we consider two cases according as Γ =0 or Γ≠0.This separates the spacetimes into conformally flat and nonconformally flat categories.
Case 1(a)When Γ=0,the spacetime becomes conformally flat and Eqs.(26)–(29)are identically satis fied.Moreover,the condition Γ=0 relates the metric functions A and B asUsing this relation,the integrability conditions(17)–(22)may be integrated to find the unknown functions F0,F4,and Fi.The procedure is explained below.
Equations(18),(20),and(22)can be easily solved to get
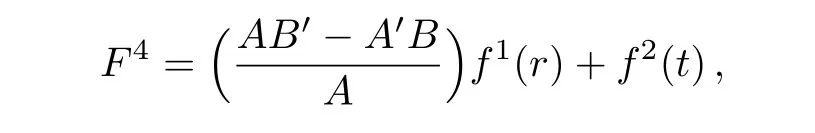
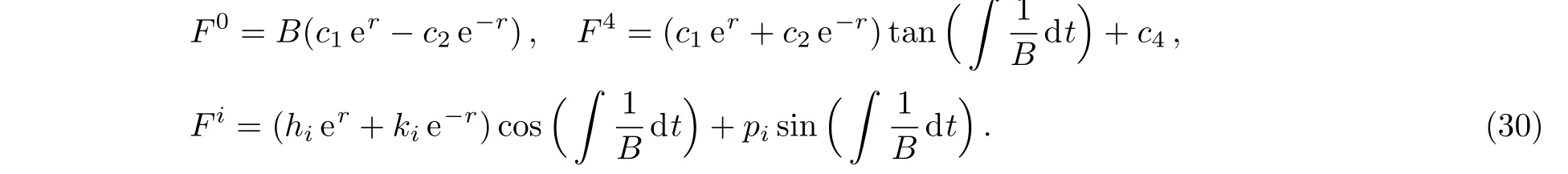
Putting back the above values in the system(16),we have:

where i=1,2,3.Thus we can state our results in terms of the following theorem.
Theorem 1The conformally flat Kantowski-Sachs metric admits a 15-dimensional Lie algebra of conformal Killing vectors,where the metric functions are related by the
Case 1(b)Here we consider the Kantowski-Sachs metric to be non-conformally flat,that is Γ≠0,and solve the system of Eqs.(26)–(29)and the integrability conditions(17)–(22).
It is straightforward to solve Eqs.(26)–(28)and obtain

where g1(r)and fi(r)are functions of integration.Thus Eq.(29)implies(Γ/A)′g1(r)=0.Considering g1(r)≠0,we have(Γ/A)′=0,which gives Γ =A.Consequently,the metric functions are related by the equation A=and we have Fi=0 and F0=
As far the integrability conditions(17)–(19)and(22)are concerned,they are identically satis fied by the above obtained values.Using these values in Eq.(20),we get
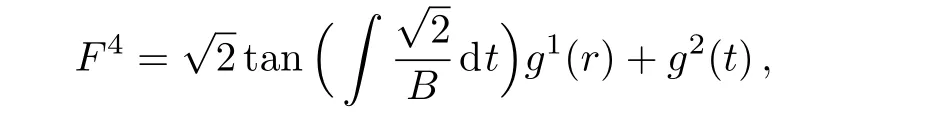
where the function g2(t)arises during integration.Finally,differentiating Eq.(21)with respect to r,we getand g2(t) =With all these values,the system(16)becomes:
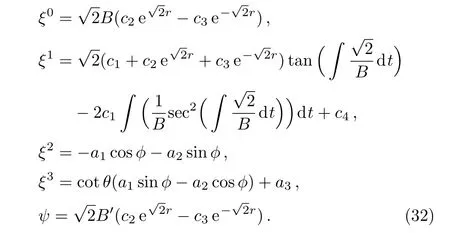
Thus we can state our results in terms of the following theorem.
Theorem 2The non-conformally flat Kantowski-Sachs metric admits a 7-dimensional Lie algebra of CKVs,where the metric functions are related by the equation A=Out of these seven CKVs, five are the KVs,which can be obtained by setting ψ=0 and the remaining two are proper CKVs.
Case 2Here we assume that A=B and A′≠0.Integrating Eq.(18),we have Fi(t,r)=fi(t)+gi(r),for i=1,2,3.The functions fi(t)and gi(r)arise in the process of integration.Simplifying Eq.(17)using this value of Fi(t,r),we getwhere c1is a separation constant.Integrating the last equation,we obtain

Thus the value of Fi(t,r)becomes
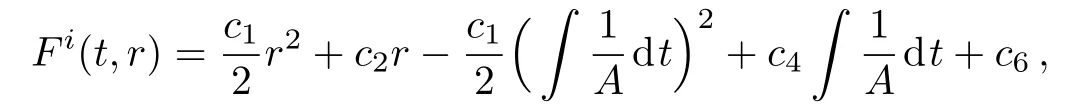
where c6=c3+c5.Substituting this value of Fi(t,r)in Eq.(19)and differentiating it twice with respect to r,we get c1=c2=c4=c6=0⇒Fi(t,r)=0,for i=1,2,3.
The functions F0(t,r)and F4(t,r)can be determined from Eqs.(20)–(22).Solving Eq.(22),one easily gets F0(t,r)=Af0(r);f0(r)being a function of integration.Using this value in Eq.(21)and integrating it with respect to t,we have F4(t,r)=(r)∫(1/A)dt+f4(r),where f4(r)is a function of integration.If we substitute these values of F0(t,r)and F4(t,r)in Eq.(20)and differentiate it with respect to t,we obtain f0(r)=c7r+c8and f4(r)=c9.Finally,we have F0(t,r)=A(c7r+c8)and F4(t,r)=c7∫(1/A)dt+c9.Thus we have the following CKVs:
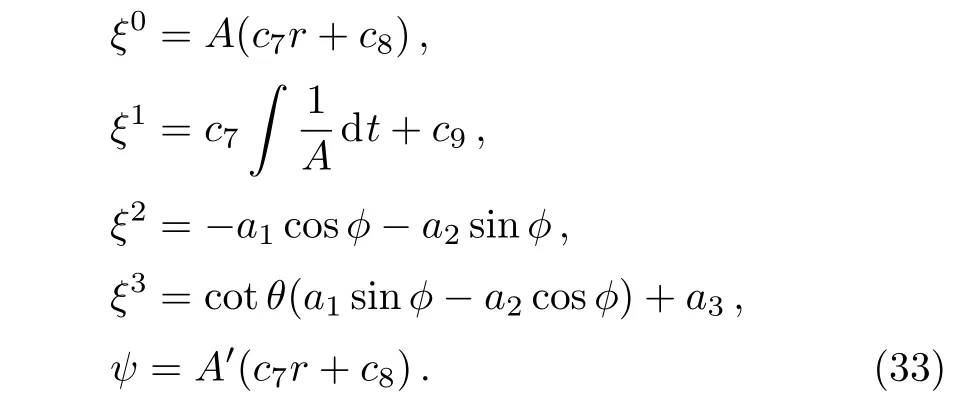
In this case,we get six CKVs out of which four are the Killing vectors as given in Eq.(5)and the remaining two are proper CKVs,which can be expressed as ξ(5)=A ∂tand ξ(6)=rA∂t+ ∫(1/A)dt∂r.
Case 3In this case,we take A′=B′=0.Solving Eqs.(17)and(22)using the same steps as in case II,we get ψ =0 and the following values of ξaare obtained:
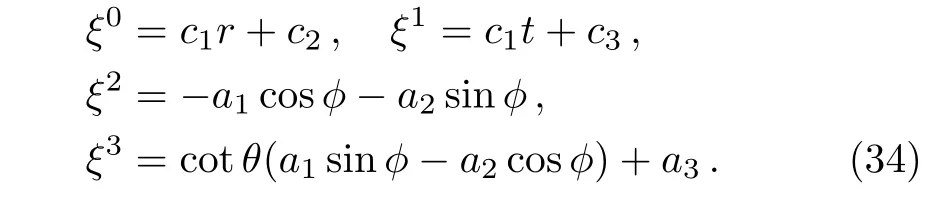
Thus no proper CKV exist in this case.We have six KVs,out of which four are same as minimum KVs of Kantowski-Sachs metric,given in Eq.(5),and the remaining two KVs can be written as ξ(5)= ∂tand ξ(6)=r∂t+t∂r.
Case 4 Here we take A′=0 and B′≠0.Solving Eq.(18),we have Fi(t,r)=(1/B)fi(r)+gi(t),where fi(r)and gi(t)are functions of integration. Using this value of Fi(t,r)in Eq.(19)and differentiating it with respect to r,we have(BB′′− B′2− 1)=0,which give rise to two cases depending upon whether BB′′− B′2− 1≠0 or BB′′− B′2− 1=0.Here we discuss both the cases.
Case 4(a)If BB′′− B′2− 1≠0,the simultaneous solution of Eqs.(17)–(19)yields Fi(t,r)=0.Moreover,solving Eqs.(21)and(22),we obtain F0(t,r)=Bf0(r)and F4(t,r)=(r)∫Bdt+f4(r).Using these values in Eq.(20)and differentiating it twice with respect to t,we get the relation(B′′/B)′f0(r)=0.If(B′′/B)′≠0,then f0(r)=0 and Eq.(20)gives f4(r)=c1.Hence the system(16)becomes:
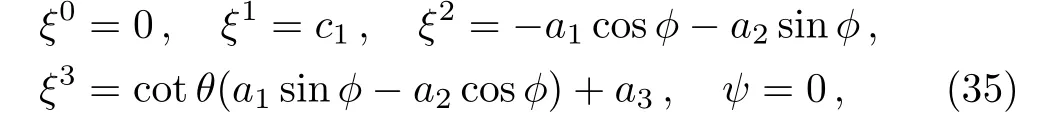
which shows that there is no proper CKV in this case and the CKVs are exactly same as the four KVs of Kantowski-Sachs metric,given in Eq.(5).
In the later case,that is when(B′′/B)′=0,the metric function B gets the value B=c1et+c2e−t,where c1c2≠1/4 and we obtain the final form of the system(16)as:

In this case,we obtain the set of minimal KVs given in Eq.(5)along with two proper CKVs,which are expressible as ξ(5)=B er∂t+B′er∂rand ξ(6)=B e−r∂t−B′e−r∂r.
Case 4(b)In this case,we have BB′′− B′2− 1=0 ⇒B=(1/2)(et+e−t)=cosht.In this case,the Weyl tensor for Kantowski-Sachs metric vanishes and we obtain 15-dimensional Lie algebra of CKVs,which is given below:
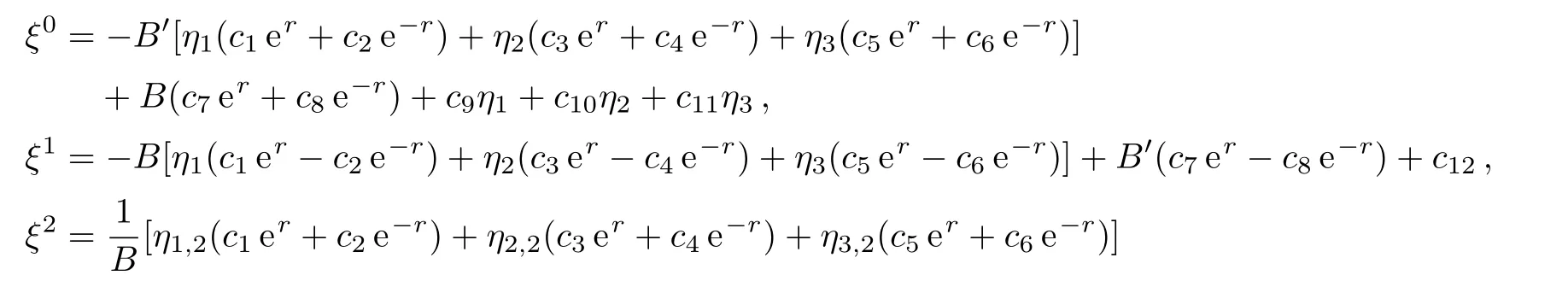

where η1,η2and η3are same as defined in Eq.(16).Out of the above 15 CKVs,seven are KVs,which can be obtained by setting ψ=0 in the above system and the remaining eight are proper CKVs.
Case 5In this case,we solve the integrability conditions by assuming that A′≠0 and B′=0.Solving Eq.(18)using these conditions,we get Fi(t,r)=A fi(r)+gi(t).Substituting this value in Eq.(19)and differentiating it with respect to r,we have=0.Like the previous case,here two sub cases arise depending upon whether A+A′′=0 or A+A′′≠0.Here we discuss both cases.
Case 5(a)If A+A′′≠0,then using some simple algebraic manipulations,the solution of Eqs.(17)–(19),(21)and(22)gives Fi(t,r)=0,F0(t,r)=f0(r)and F4(t,r)=(r)∫(1/A2)dt+f4(r).Using these values in Eq.(20)and differentiating it twice with respect to t,we get(AA′′− A′2)′f0(r)=0.If we assume that(AA′′− A′2)′≠0,then f0(r)=0 and Eq.(20)gives f4(r)=c1.Hence the system(16)becomes:
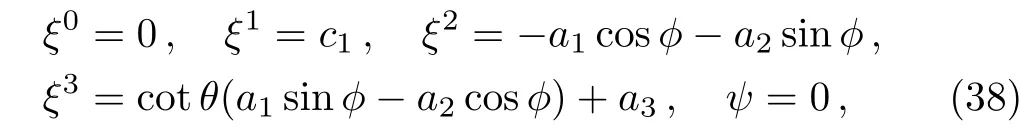
which shows that in this case,the CKVs are exactly same as the four minimal KVs of Kantowski-Sachs metric,given in Eq.(5).There exist no proper CKV.
In the later case,we have(AA′′− A′2)′=0 ⇒ A=cosht.For this value of A,a complete solution of the integrability conditions(17)–(22)gives:
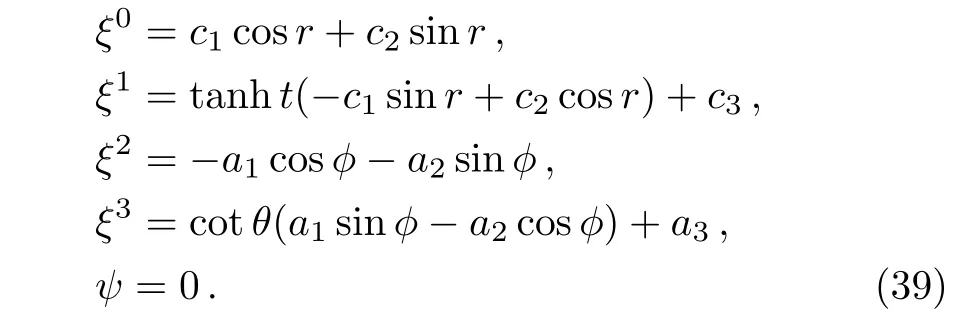
Like the above case,there is no proper CKV and the CKVs become KVs,which are six in number. Four KVs are same as given in Eq.(5)and the remaining two can be written as ξ(5)=cosr∂t− sinrtanht∂rand ξ(6)=sinr∂t+cosrtanht∂r.
Case 5(b)In this case,we have A= β1cost+β2sint and the Kantowski-Sachs metric is conformally flat.Considering β1= β2=1 and solving the integrability conditions(17)–(22),we get the following 15-dimensional Lie algebra of CKVs:
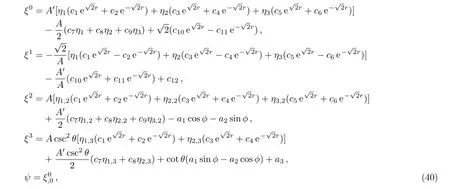
where η1, η2and η3are same as defined in Eq.(16).Out of the above 15 CKVs,six are KVs,which can be obtained by setting ψ=0 in the above system and the remaining nine are proper CKVs.
3 Inheriting Conformal Killing Vectors
In this section,we study the inheriting conformal Killing vectors in Kantowski-Sachs metric by choosing thefluid four velocity as ua=From Eq.(3),we obtain:

which shows that ξ0is dependent on t only.Thus in the system(16),we must have=0 and F0=F0(t).Using Eqs.(19)and(21),we get Fi(t,r)=0 and F4=F4(r).Therefore,we are left with the only two integrability conditions,which are given below:
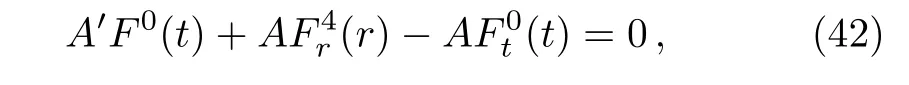

It is straightforward to solve the above two equations and get F0(t)=B,F4(r)=c1r+c2and B=c1A∫(1/A)dt+c3A.Hence the system (16)reduces to:
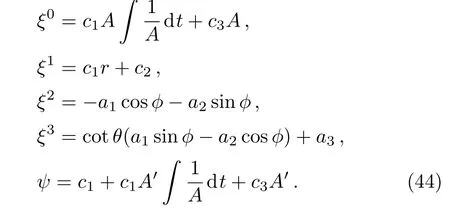
From above,we can see that the Kantowski-Sachs metric admits six ICKVs,provided that the metric functions satisfy the relation B=c1A∫(1/A)dt+c3A.Out of these six ICKVs,four are the KVs as mentioned in Eq.(5)and the remaining two are proper ICKVs,which can be written as ξ(5)=A∂tand ξ(6)=A∫(1/A)dt∂t+r∂r.
4 Summary
In our present work,the CKVs in Kantowski-Sachs metric have been investigated. The conformal Killing equations are solved in different cases and it is concluded that the non-conformally flat Kantowski-Sachs metric admits two proper CKVs(see cases 1(b),2,and 4(a))or otherwise the CKVs reduce to the KVs.Moreover,when the Kantowski-Sachs metric becomes conformally flat,it admits a 15-dimensional Lie algebra of CKVs,which verifies the Hall’s statement[1](see cases 1(a),4(b)and 5(b)).The number of KVs for non-conformally flat Kantowski-Sachs metric turned out to be four, five or six,while for conformally flat Kantowski-Sachs metric this number is either six or seven.
Interestingly,the classification of the conformal geometry in terms of the Weyl tensor led us to a simple and general relationships between the metric functions A and B.This may enable us to identify the known exact solutions of the Einstein field equations and we may write these equations in terms of a single gravitational potential.Moreover,we may apply the conformal symmetries found in this paper to generate exact solutions of the Einstein field equations.
The inheriting CKVs are also studied and it is shown that if the metric functions of the Kantowski-Sachs metric are related by B=c1A∫(1/A)dt+c3A,then it admits six ICKVs out of which two are proper ICKVs and four are the basic KVs of Kantowski-Sachs metric.
The authors are thankful to the unknown referees for their invaluable suggestions because of which the manuscript is significantly improved.
[1]G.S.Hall,Symmetries and Curvature Structure in General Relativity,World Scientific,London(2004)
[2]A.Z.Petrov Einstein Spaces,Oxford University Press,Pergamon(1969)
[3]R.Maartens,D.P.Mason,and M.Tsamparlis,J.Math.Phys.27(1986)2987.
[4]D.P.Mason and R.Maartens,J.Math.Phys.27(1986)2511.
[5]F.Rahaman,M.Jamil,R.Sharma,and K.Chakraborty Astrophys.Space Sci.330(2010)249.
[6]F.Rahaman,M.Jamil,M.Kalam,et al.,Astrophys.Space Sci.325(2010)137.
[7]M.Esculpi and E.Aloma,Eur.Phys.J.C 67(2010)521.
[8]A.A.Usmani,F.Rahaman,S.Ray,et al.,Phys.Lett.B 701(2011)388.
[9]R.Maartens and S.D.Maharaj,Class.Quantum Grav.3(1986)1005.
[10]R.Maartens and S.D.Maharaj,Class.Quantum Grav.8(1991)503.
[11]S.Moopanar and S.D.Maharaj,J.Eng.Math.82(2013)125.
[12]D.Kramer and J.Carot,J.Math.Phys.32(1991)1857.
[13]T.Hussain,S.Khan,A.H.Bokhari,and G.A.Khan,Theor.Math.Phys.191(2017)620.
[14]S.Khan,T.Hussain,A.H.Bokhari,and G.A.Khan,Commun.Theor.Phys.65(2016)315.
[15]S.Khan,T.Hussain,A.H.Bokhari,and G.A.Khan,Eur.Phys.J.C 75(2015)523.
[16]A.A.Coley and B.O.J.Tupper,Class.Quantum Grav.7(1990)1961.
[17]A.A.Coley and B.O.J.Tupper,Class.Quantum Grav.7(1990)2195.
[18]A.A.Coley and B.O.J.Tupper,Class.Quantum Grav.11(1994)2553.
[19]L.Herrera,J.Jimenez,L.Leal,and J.Ponce de Leon,J.Math.Phys.25(1984)3274.
[20]R.Kantowski and R.K.Sachs,J.Math.Phys.7(1966)443.
 Communications in Theoretical Physics2018年4期
Communications in Theoretical Physics2018年4期
- Communications in Theoretical Physics的其它文章
- Melting Heat in Radiative Flow of Carbon Nanotubes with Homogeneous-Heterogeneous Reactions
- Effects of a Weakly Interacting Light U Boson on Protoneutron Stars Including the Hyperon-Hyperon Interactions∗
- Direct Urca Processes Involving Proton1S0Superfluidity in Neutron Star Cooling∗
- Controlling Thermal Conduction by Graded Materials∗
- Influence of Non-linear Radiation Heat Flux on Rotating Maxwell Fluid over a Deformable Surface:A Numerical Study
- Effects of Low Anisotropy on Generalized Ghost Dark Energy in Galileon Gravity
