Travelingwave solutionstosome nonlinear fractional partialdifferential equationsthroughtherational(G ′ /G ) -expansionmethod

Trikul Islm M. Ali Akr Aul Klm Azd

a Department of Mathematics, Hajee Mohammad Danesh Science and Technology University, Dinajpur, Bangladesh

b Department of Applied Mathematics, Rajshahi University, Rajshahi, Bangladesh

1.Introduction

The behavior of natural phenomena at scales small enough can noticeably be described by fractional order differential equation than the differential equation of integer order. The necessity of fractional derivatives becomes apparent in modeling of electrical and mechanical properties of real materials, as well as in the description of rheological properties of rocks. As a result, fractional differential equations have gained considerable popularity and importance due to its realistic application in various fi elds of science and engineering and have proved to be valuable tools for the modeling of many physical phenomena. In the last few decades, many researchers paid deep attention to examine closed form traveling wave solutions to the nonlinear partial differential equations(NPDEs) of fractional order and analyze the physical phenomena relevance to science and engineering. Therefore, in literature they have made a signi fi cant contribution to construct the exact solutions of nonlinear fractional differential equations of physical interest. Nonlinear fractional equations have become the focus of many researches due to their frequent appearance in various applications, such as in the signal processing, control theory, systems identi fi cation, solid state physics, condensed matter physics, plasma physics, optical fi bers, chemical kinematics, electrical circuits, bio-genetics,fl uid fl ow and other areas [1–3] . The closed form wave solutions of the equations [4–7] are deeply helpful to comprehend the mechanisms of the phenomena as well as their further application in practical life. Several powerful and ef fi cient methods have been proposed by many researchers to investigate the exact traveling wave solutions of integer order and also fractional order NPDEs; as for instance the fractional subequation method [8,9] , the Adomian decomposition method[10,11] , the variational iteration method [12–14] , the (G′/G)-expansion method and its various modi fi cations [15–17] , the homotopy perturbation method [18–20] , the differential transformation method [21,22] , the fi nite element method [23] , the fi nite difference method [24] , the Exp-function method [25–29] , the method of lines [30,31] , the He’s polynomial [32] ,the reproducing kernel method [33–35] , the solitary ansatz approach and the Hirota bilinear method [36] , the extended tanh and hirota method [37] , the extended modi fi ed direct algebraic method [38–40] , the reductive perturbation method [41–43] , the modi fi ed extended tanh function method [44,45] , the exp(-φ(ξ))-expansion method [46,47] , the auxiliary equation method [48,49] , the modi fi ed simple equation method[50] and others [51–58] .

In this article, our aim is to examine new and further general closed form traveling wave solutions to some fractional NPDEs, namely the space-time fractional foam drainage equation and the space-time fractional symmetric regularized long wave (SRLW) equation in the sense of conformable fractional derivative [59] . The conformable fractional derivative of a functionf: [0, ∞ ) →Rof orderαis de fi ned as:

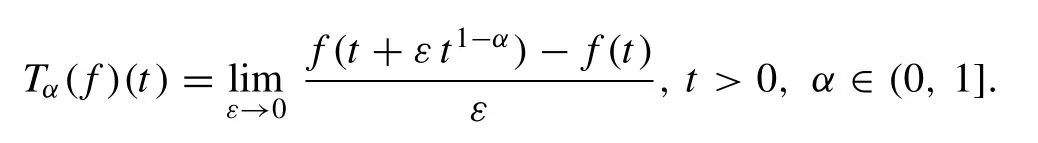
If the above limit exists, thenfis calledα-differentiable.Letα∈ (0, 1] andf,gbeα-differentiable at a pointt＞0, thenTαsatis fi es the following properties:

(i)Tα(af+bg)=aTα(f)+bTα(g), for alla,b∈R

(ii)Tα(tp)=ptp-α, for allp∈R

(iii)Tα(λ)= 0, for all constant functionsf(t)=λ

(iv)Tα(fg)=fTα(g)+gTα(f)

(v)Tα(f/g)= {gTα(f)-fTα(g)}/g2

(vi) If, in addition,fis differentiable, thenTα(f)(t)=

We employ the recently established rational (G′/G)-expansion method [60] which provides new and more general closed form traveling wave solutions to the equations mentioned above.

whereui=ui(t,x1,x2,...,xn),i= 1,...,kare unknown functions,Fis a polynomial inuiand it’s various partial derivatives including the derivatives of fractional order.

Step 1:Let us consider the nonlinear fractional composite transformation

Eq. (1) , with the aid of transformation (2) is turned into the following ordinary differential equation of integer order with respect to the variableξ:

Step 2:For convenient, we integrate Eq. (3) one or more times as possibility and integral constant can be set to zero as soliton solutions are sought.

Step 3:We reveal the solution of Eq. (3) in terms of (G′/G)as follows [48] :

whereanandbnare non-zero constants to be determined later andG=G(ξ)satis fi es the second order ODE:

whereλandμare real constants.

Eq. (5) can be re-written as

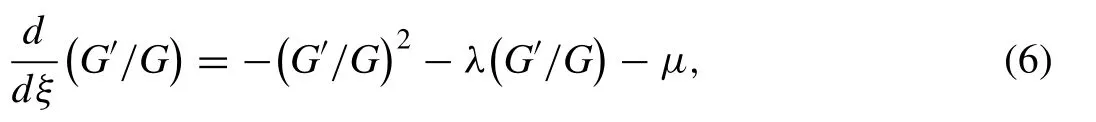
whose general solutions are given by

2.Delineation of the method

In this section, the main steps of the rational (G′/G)-expansion method is discussed for fi nding exact analytic solutions of nonlinear partial differential equations of fractional order.

Suppose a fractional partial differential equation in the independent variablest,x1,x2,...,xnis given as follows:

whereAandBare arbitrary constants.

Step 4:To determine the positive integern, we substitute(4) along with (5) into (3) and balance between the highest order derivatives and the highest order nonlinear terms appearing in (3) . Furthermore, if the degree ofu(ξ) is de fi ned as deg [u(ξ)] =n, the degree of the other expressions are as follows:

Step 5:Substituting (4) together with (5) into (3) , we obtain a polynomial equation with indeterminate (G′/G). Setting each coef fi cient of (G′/G) to zero gives a system of algebraic equations. Solve this system of equations forai,bi,λ, andμby means of the symbolic computation software, such as Maple 13.

Step 6:We use the values ofai,bi,λ, andμtogether with(7) into (4) to obtain the closed form traveling wave solutions of the nonlinear fractional partial differential Eq. (1) .

3.Implementation of the method

In this section, we make use the rational (G′/G)-expansion method to construct the general closed form traveling wave solutions to the nonlinear space-time fractional foam drainage equation and space-time fractional symmetric regularized long wave (SRLW) equation.

3.1. The space-time fractional foam drainage equation

Consider the space-time fractional foam drainage[61,62] equation

Eq. (8) has appeared as a simple model for describing the fl ow of liquid through channels and nodes between the bubbles, driven by gravity and capillarity. The fractional complex transformation

wherekandlare constants, permit us to reduce Eq. (8) into the following ODE:

Balancing the highest order derivative and the nonlinear term appearing in Eq. (10) , we deduce thatn= 1 . Thus, the solution of Eq. (4) reduces to the form

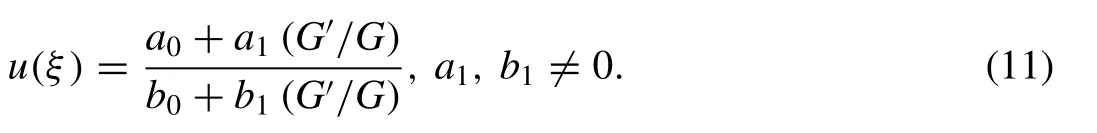
Substituting (11) into (10) , the left hand side becomes a polynomial in (G′/G). Setting each coef fi cient of this polynomial to zero, yields a set of algebraic equations (for simplicity, we omit them to display) fora0,b0,a1,b1,k,l. Solving this over-determined set of equations with the aid of computer algebra, like Maple 13, provides the following results:

whereb0,b1,k,λandμare arbitrary constants.

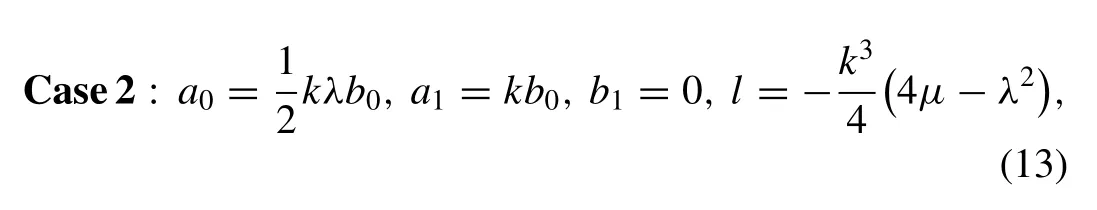
whereb0,k,λandμare arbitrary constants.

whereb1,k,λandμare arbitrary constants.

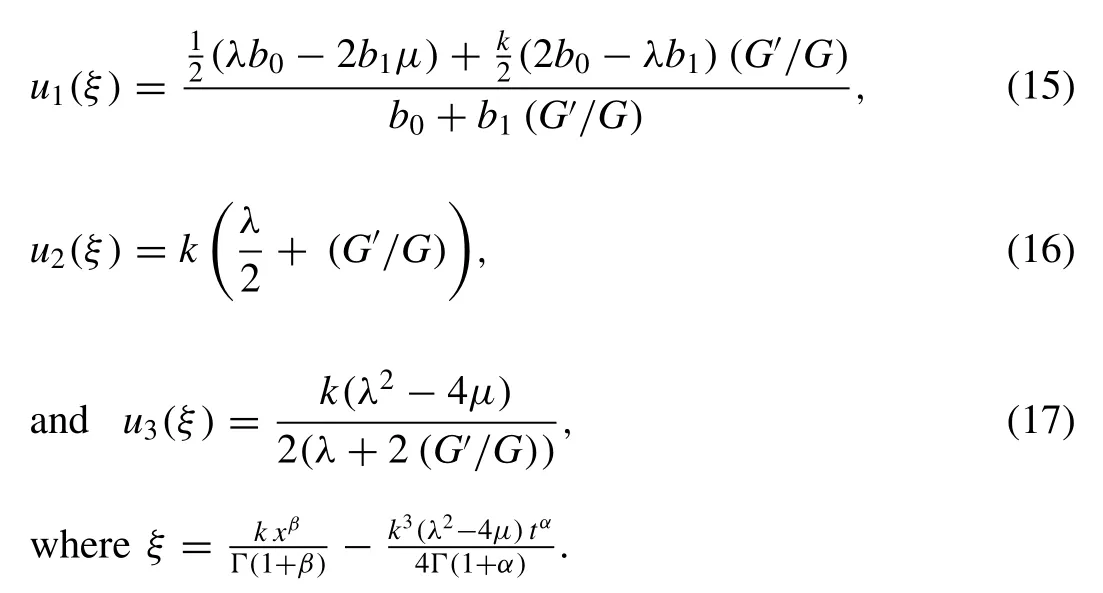
Now, using the solutions assembled in (15) - (17) and simplifying, we achieve the following nine types of traveling wave solutions:

For case 1:

Whenλ2-4μ＞0, the hyperbolic function solution becomes

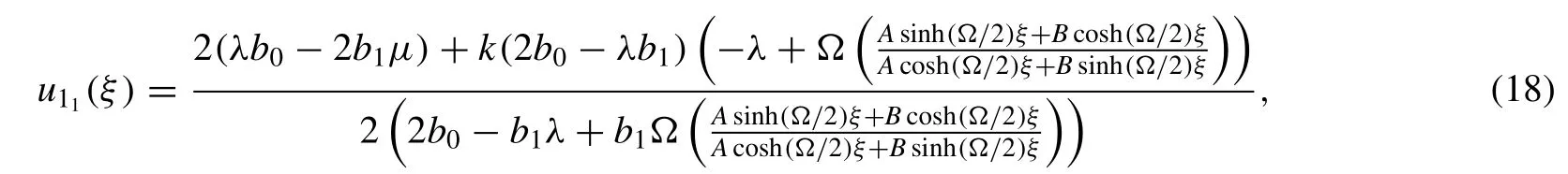
whereAandBare arbitrary constants. SinceAandBare arbitrary constants one might arbitrarily choose their values. Thus, if we chooseA/= 0 butB= 0, then after simpli fi cation, solution (18) becomes

Settingλ=4,μ=3 ,k=1 ,b0=b1=1/2 into solution(19) and simplifying,we attain

Whenλ2-4μ＜0, the trigonometric function solution is found in the form of

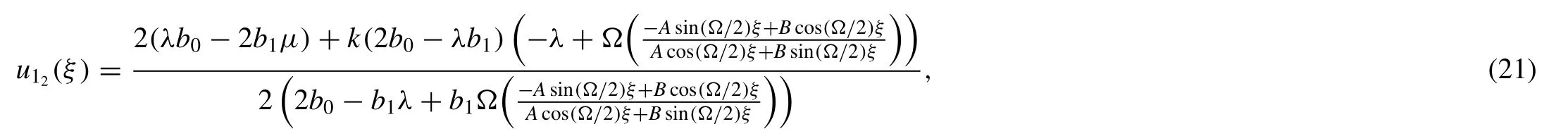
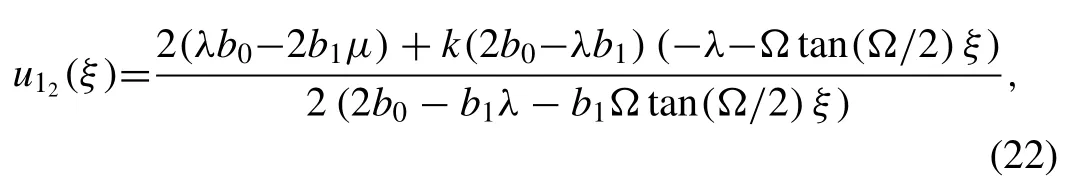
Settingλ= 4,μ= 8 ,k= 1 ,b0=b1= 1/2 into solution(22) and simplifying, we attain

4月19日，水利部部长、部抗震救灾领导小组组长陈雷主持召开水利部抗震救灾领导小组第二次全体会议，认真学习贯彻4月17日中共中央政治局常委会议重要部署和胡锦涛总书记关于抗震救灾的重要指示精神，进一步安排部署下一步水利抗震救灾工作。

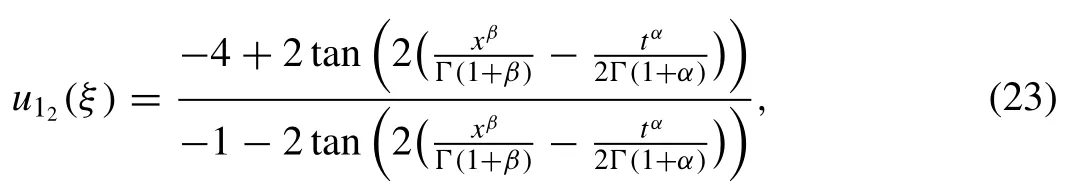
Whenλ2-4μ= 0, we obtain the rational solution as

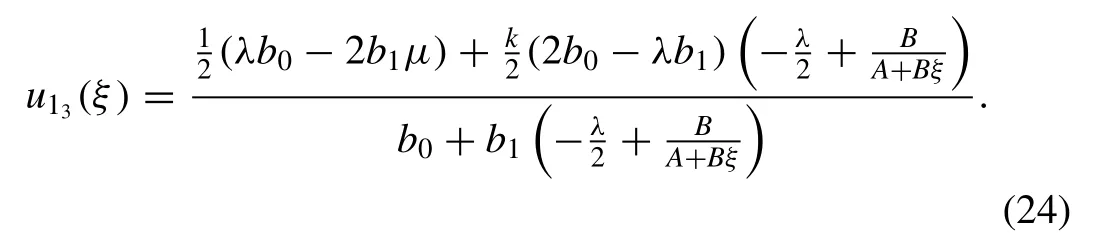
Settingλ= 2,μ= 1 ,k= 1 ,b0= 1/2,b1= 1 ,A= 0 in solution (24) and simplifying, we attain

For cases 2 and 3, we might also achieve three types of closed form traveling wave solutions, such as hyperbolic function solution, trigonometric function solution and rational function solution. But, the solutions for cases 2 and 3 have not been recorded to evade the displeasure to the readers. The results obtained above are new and further general than the existing results.

3.2. The space-time fractional symmetric regularized long wave (SRLW) equation

Let us consider the space-time fractional symmetric regularized long wave (SRLW) equation

which arises in several physical applications including ion sound waves in plasma. This equation describes weakly nonlinear ion acoustic and space-charge waves and the real-valuedu(x,t) corresponds to the dimensionless fl uid velocity with a decay condition.

Introducing the fractional complex transformation

wherekandcare constants, Eq. (26) reduces to the following ODE:

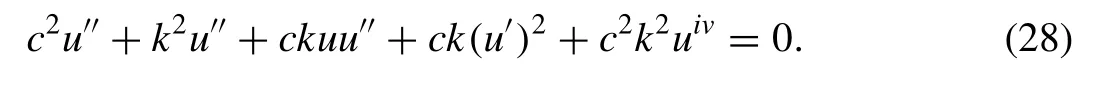
Integration of Eq. (28) twice yields,

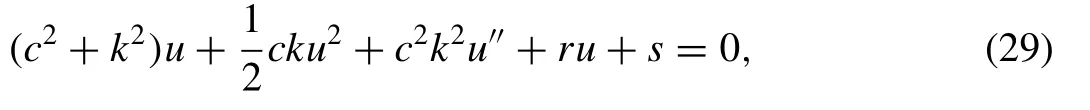
whererandsare integral constants. Applying the homogeneous balance method to Eq. (29) reduces the solution of Eq. (4) into the form

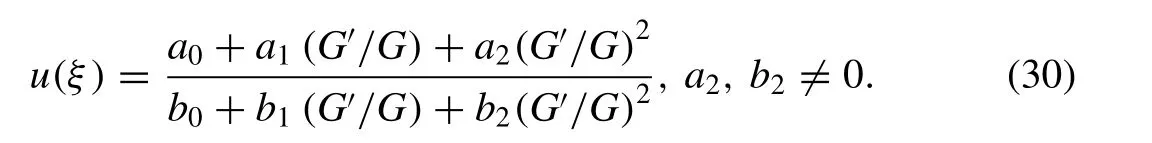
Inserting solution (30) into Eq. (29) possesses a polynomial equation in (G′/G) and setting the coef fi cients of like terms to zero, yields a set of algebraic equations (for minimalism, we omit them to exhibit) fora0 ,b0 ,a1 ,b1 ,a2 ,b2 ,c,k,r,s.Solving this set of equations with the aid of symbolic computer software, like Maple 13, provides the following results:

whereb0,c,k,λandμare all arbitrary constants.

Putting the values set out in (31) into solution of Eq. (30) ,give

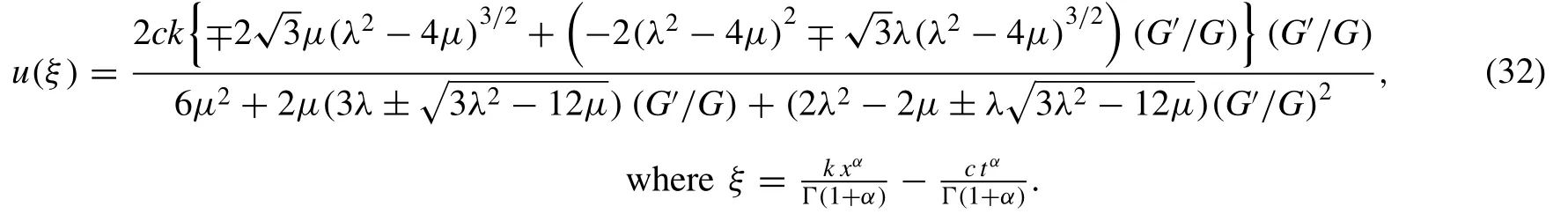
Now, making use the solutions provided in (7) into(32) and simplifying, we achieve the following traveling wave solutions:

Whenλ2-4μ＞0, the hyperbolic function solution becomes

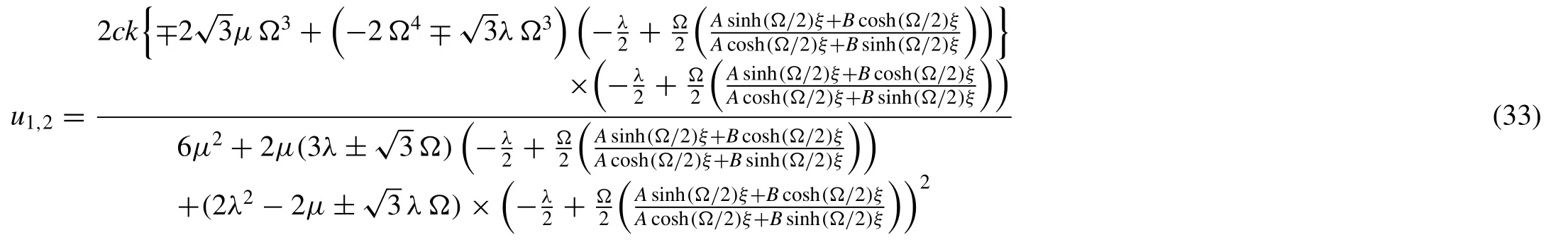
Whenλ2-4μ＜0, the trigonometric function solution becomes

The results obtained above are new and more general than the existing results.

Whenλ2-4μ= 0, then from (31) , it can be founda0=0,a1= 0,a2= 0 and thusu(ξ)= 0. Therefore, this trivial solution has not been written here.

4.Conclusion

In this article, we investigated the exact traveling wave solutions to some NPDEs of fractional order, namely the spacetime fractional foam drainage equation and the space-time fractional symmetric regularized long wave (SRLW) equation by the recently established rational (G′/G)-expansion method.Three types of closed form analytical solutions including the generalized hyperbolic function solutions, trigonometric function solutions and rational solutions are successfully constructed for the fractional equations mentioned above which are very promising and encouraging. The obtained solutions might be signi fi cant to analyze the fl ow of liquid through channels and nodes between the bubbles driven by gravity and capillarity, weakly nonlinear ion acoustic and space-charge waves and the dimensionless fl uid velocity with a decay condition. To the best of our knowledge, the results achieved in this article have not been reported in the earlier literature.The suggested method can be employed to construct new and further general traveling wave solutions of the obstacle, unilateral, free, moving, and contact problems which arises in various branches of science and engineering.

Acknowledgment

The authors wish to take this opportunity to express their sincere gratitude to the anonymous referees for their valuable comments and suggestions that greatly improved the manuscript.

[1] I. Podlubny , Fractional Differential Equations, vol. 198 of Mathematics in Science and Engineering, Academic Press, San Diego, Calif, USA,1999 .

[2] X.J. Yang , Local Fractional Functional Analysis and Its Applications,Asian Academic Publisher, Hong Kong, 2011 .

[3] X.J. Yang , Advanced Local Fractional Calculus and Its Applications,World Science Publisher, New York, NY, USA, 2012 .

[4] W.X. Ma , B. Fuchssteiner , Int. J. Nonlin. Mech. 31 (1996) 329–338 .

[5] W.X. Ma , DT Zhou , Acta Math. Scita. 17 (1997) 168–174 .

[6] W.X. Ma , Phys. Lett. A 301 (2002) 35–44 .

[7] W.X. Ma , Phys. A 343 (2004) 219–237 .

[8] S. Zhang , H.Q. Zhang , Phys. Lett. A 375 (2011) 1069–1073 .

[9] S. Guo , L. Mei , Y. Li , Y. Sun , Phys. Lett. A 376 (2012) 407–411 .

[10] Y. Hu , Y. Luo , Z. Lu , J. Comput. Appl. Math. 215 (2008) 220–229 .

[11] A.M.A. El-Sayed , S.H. Behiry , W.E. Raslan , Comput. Math. Appl. 59(2010) 1759–1765 .

[12] M. Inc , J. Math. Anal. Appl 345 (2008) 476–484 .

[13] Z. Odibat , S. Momani , Comput. Math. Appl. 58 (2009) 2199–2208 .

[14] S.T. Mohyud-Din , M.A. Noor , K.I. Noor , M.M. Hosseini , Int. J. Nonlinear Sci. Numer. Simul. 11 (2010) 87–92 .

[15] J. Feng , W. Li , Q. Wan , Appl. Math. Comput. 217 (2011) 5860–5865 .

[16] B. Zheng , Commun. Theor. Phys. 58 (2012) 623–630 .

[17] M.N. Alam , M.A. Akbar , S.T. Mohyud-Din , Chin. Phys. B 23 (2014)020203 .

[18] K.A. Gepreel , Appl. Math. Lett. 24 (2011) 1428–1434 .

[19] S.T. Mohyud-Din , A. Yildirim , S. Sariaydin , Int. J. Numer. Methods Heat Fluid Flow 21 (2011) 272–281 Emerald .

[20] S.T. Mohyud-Din , A. Yildirim , S.A. Sezer , Int. J. Numer. Methods Heat Fluid Flow 21 (2011) 822–827 .

[21] S. Momani , Z. Odibat , V.S. Erturk , Phys. Lett. A 370 (2007) 379–387 .

[22] Z. Odibat , S. Momani , Appl. Math. Lett. 21 (2008) 194–199 .

[23] W. Deng , SIAM J. Numer. Anal. 47 (2008) 204–226 .

[24] G.H. Gao , Z.Z. Sun , Y.N. Zhang , J. Comput. Phys. 231 (2012)2865–2879 .

[25] S.T. Mohyud-Din , Y. Khan , N. Faraz , A. Yildirim , Int. J. Numer. Methods Heat Fluid Flow 22 (2012) 335–341 .

[26] M.A. Noor , S.T. Mohyud-Din , A. Waheed , E.A. Al-Said , Appl. Math.Comput. 216 (2010) 477–483 Elsevier .

[27] S.T. Mohyud-Din, M.A. Noor, K.I. Noor, Math. Problems Eng. 2009(2009) 234849 Hindawi 25 pages, doi: 10.1155/ 2009/ 234849.

[28] M.A. Noor , S.T. Mohyud-Din , A. Waheed , Acta Appl. Math. 104 (2008)131–137 Springer .

[29] S.T. Mohyud-Din , M.A. Noor , A. Waheed , Z. Naturforsch. A –J. Phys.Sci. 65a (2010) 78–84 .

[30] S.T. Mohyud-Din , E. Negahdary , M. Usman , Int. J. Numer. Methods Heat Fluid Flow 22 (2012) 641–658 .

[31] M.S. Hashemi , M. Inc , E. Karatas , A. Akgul , J. Adv. Phys. 6 (2017)413–417 .

[32] S.T. Mohyud-Din , M.A. Noor , K.I. Noor , Int. J. Nonlinear Sci. Numer.Simul. 10 (2009) 223–229 .

[33] A. Akgul, M. Inc, E. Karatas, D. Baleanu, Adv. Diff. Equ. 2015 (2015)220, doi: 10.1186/s13662- 0015- 0558- 8 .

[34] A. Akgul , M. Inc , E. Karatas , DCDS-S Impact Factor 2014 (2015)0.567 .

[35] A. Akgul , Y. Khan , E.K. Akgul , D. Baleanu , M.M.A. Qurashi , J. Nonlinear Sci. Appl. 10 (2017) 4408–4417 .

[36] M. Inc , B. Kilic , E. Karatas , A. Akgul , J. Adv. Phys. 6 (2017) 288–293 .

[37] M. Inc , B. Kilic , E. Karatas , Open Phys. 14 (2016) 76–80 .

[38] A.R. Seadawy , Comput. Math. Appl 70 (2015) 345–352 .

[39] M. Arshad , A.R. Seadawy , L. Dianchen , J. Wang , Results Phys. 6 (2016)1136–1145 .

[40] A.R. Seadawy , M. Arshad , L. Dianchen , Eur. Phys. J. Plus 132 (162)(2017) 1–20 .

[41] A.R. Seadawy , Comput. Math. Appl. 71 (2016) 201–212 .

[42] A.R. Seadawy , Stat. Mech. Appl. Phys. A 455 (2016) 44–51 .

[43] E.S. Selima , A.R. Seadawy , X. Yao , Eur. Phys. J. Plus 131 (2016) 425 .

[44] M.M.A. Khater , J. Appl. Math. Bioinf. 6 (2016) 37–48 .

[45] E.H.M. Zahran , M.M.A. Khater , Appl. Math. Modell. 40 (2016)1769–1775 .

[46] A.R. Seadawy , D. Lu , M.M.A. Khater , J. Ocean Eng. Sci. 2 (2017)137–142 .

[47] M.M.A. Khater , Cogent Math. 3 (2016) 1–16 .

[48] A.R. Seadawy , Eur. Phys. J. Plus 132 (2017) 29 .

[49] A.R. Seadawy , L. Dianchen , Results Phys 6 (2016) 590–593 .

[50] M.M.A. Khater , Global J. Sci. Front. Res. (F) 15 (2015)ISSN:2249-4626 .

[51] W.X. Ma , Y. You , Trans. Am. Math. Soc. 357 (2004) 1753–1778 .

[52] W.X. Ma , Y. You , Solitons Fractals 22 (2004) 395–406 .

[53] W.X. Ma , H. Wu , J. He , Phys. Lett. A 364 (2007) 29–32 .

[54] D. Lu , A.R. Seadawy , M.M.A. Khater , Results Phys. 7 (2017)2028–2035 .

[55] A.R. Seadawy , D. Lu , M.M.A. Khater , Optik –Int. J. Light Electron Opt. 143 (2017) 104–114 .

[56] A.R. Seadawy , Optik – Int. J. Light Electron Opt. 139 (2017) 31–43 .

[57] A.R. Seadawy, Math. Met. Appl. Sci. 40 (2017) 1598–1607.

[58] A.R. Seadawy , K.E. Rashidy , Pramana –J. Phys. 87 (2016) 20 .

[59] R. Khalil , M.A. Horani , A. Yousef , M. Sababheh , J. Comput. Appl.Math. 264 (2014) 65–67 .

[60] M.T. Islam , M.A. Akbar , A.K. Azad , Nonlinear Stud. 6 (2015) 1–11 .

[61] K.A. Gepreel , S. Omran , Chin. Phys. B 21 (2012) 110204 .

[62] Z. Dahmani , M.M. Mesmoudi , R. Bebbouchi , E. J. Qual. Theory Diff.Equ. 30 (2008) 1–10 .