揭秘当年费尔马(Fermat)大定理的证明思路与绝妙方法
——不定方程xn+yn=zn在n为大于2的任意整数时没有不为零的整数解
邹继芳
(辽宁省抚顺矿业集团有限责任公司机械制造厂 113001)
费尔马大定理即不定方程xn+yn=zn在n为大于2的任意整数时没有不为零的整数解.它来源是:在1621年费尔马在巴黎买了一本丢番图(公元三世纪时古希腊数学家)所作的《算术》的法文译本.这本书的第二卷中提出了求不定方程X2+Y2=Z2的整数解问题,他把他思考的心得记在这本《算术》第二册一页书的空白处,他写到“不可能把一个整数的立方表示成两个整数的立方和;也不可能把一个整数的四次幂表示成两个整数的四次幂之和;一般地说不可能把任意一个次数大于2的方幂表示成两个同次方幂之和”.这也就是说不定方程xn+yn=zn,在n为大于2的任意整数时没有不为零的整数解.
费尔马逝世后,人们在他的图书室找到了那本书,写在书上的结论也公诸于世了.这个结论是一个未经证明的数学猜测,后人把这个数学史上著名的猜测称为“费尔马大定理”.费尔马在那页书上继续写道“我发现了这个论断的奇妙证明,但这里空白太窄,写不下了”.人们找遍了他遗留下来的手稿,始终没有能够找到他对这个问题的“奇妙证明”.人们只有自己来弄清这是一个正确的定理还是一个错误的猜想.三百多年来,它一直是数学史上的一件悬案.
一、教学与研究(解析费尔马大定理)
费尔马在仔细研究求不定方程X2+Y2=Z2的整数解后得出了费尔马大定理:“不可能把一个整数的立方表示成两个整数的四次幂之和,一般的说,不可能把任意一个次数大于2的方幂表示成两个同次方幂之和.” 这也就是说不定方程xn+yn=zn在n大于2的任意整数时,没有不为零的整数解.
如果对费尔马大定理进行求证,我们就必须要仔细分析费尔马大定理这个问题的性质、逻辑推理,寻求证明方法,最后,进行总结和归纳的过程.
1.仔细分析和研究费尔马大定理的性质
我们知道:费尔马大定理的不定方程为
xn+yn=zn(n>2).
当n=2时可写成X2+Y2=Z2.
它不仅仅代表一个三元二次不定方程,它的几何意义是代表一个直角三角形,X、Y、Z分别代表直角三角形的三条边,三条边之间的关系为X2+Y2=Z2,这就是著名的毕达哥拉斯定理,如果求三条边的整数解,其三条边的整数解通解为, 当X、Y、Z互质时,

上式也称为勾股数组,这个结论很重要,在以后的证明过程中会经常用到.用几何表示为

(毕达哥拉斯定理几何关系)(勾股数组关系)记为(2ad、d2-a2、d2+a2)
我们可以把这个三角形称为基本直角三角形.
当n=2t(t为大于1的自然数)费尔马大定理不定方程为

符合上述基本三角形的形式.
此时用几何表示为
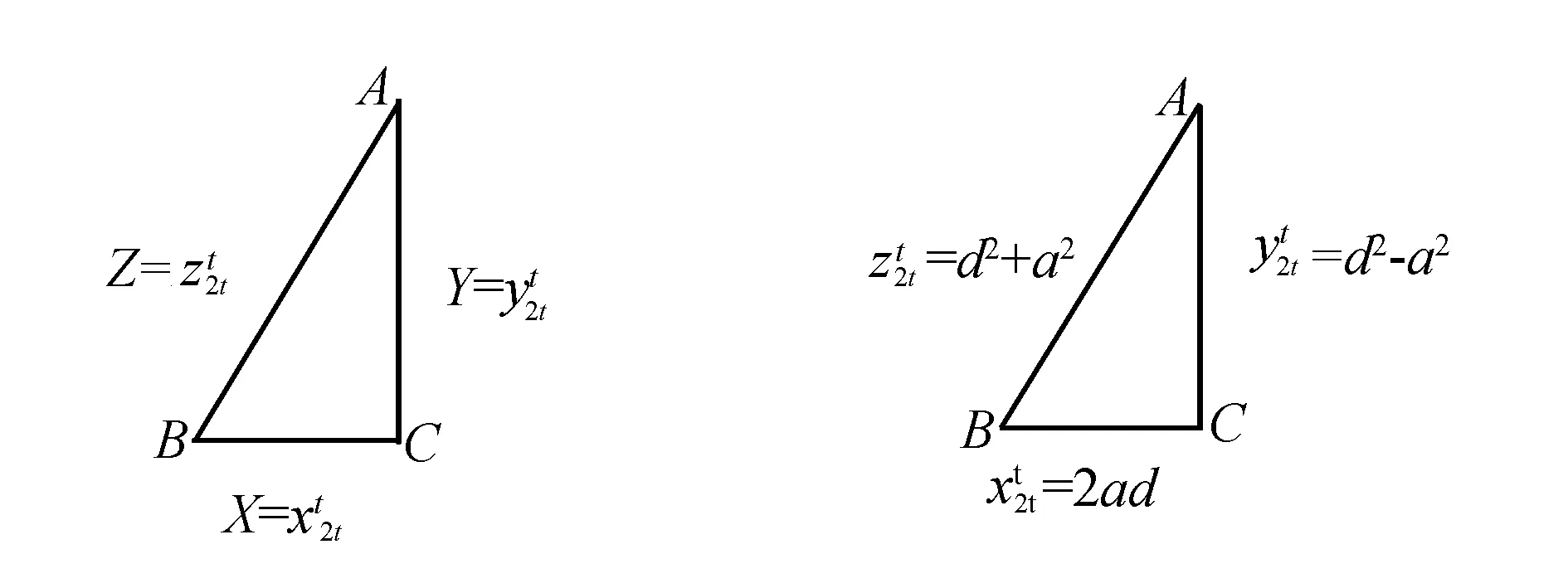

当n=2t+1时(t为任意自然数)费尔马大定理不定方程为

符合上述基本三角形的形式,此时用几何表示为



2.结论
通过上述的分析和研究可知:费尔马大定理的不定方程都是建立在基本直角三角形基础上的,只是对应的直角三角形三条边表现形式不同而已,其三条边的整数解都必须满足于勾股数组的通解条件,即有如下的关系式
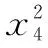
以上推理过程中,概括起来说明.当n=2t+1时,通过逻辑推理,可转换成当n=2t时的情形.当n=2t时,通过逻辑推理,可转换成当n=4时的情形.从上式中的推论中可知,只要求出当n=4时没有不为零的整数解就可以证明当n>2时没有不为零的整数解.证明过程详见x4+y4=z4没有不为零的整数解的证明过程.
二、奇妙求证x4+y4=z4不定方程对任意正整数时没有不为零的整数解
不定方程x4+y4=z4可以等价变换为
(x2)2+(y2)2=(z2)2.
此时该不定方程满足于X2+Y2=Z2的形式,
此时:X=x2,Y=y2,Z=z2.
根据X2+Y2=Z2的通解,可知

从(2)中可知d2=y2+a2,
从(3)中可知z2=d2+a2.

可见(4)(5)两方程皆符合X2+Y2=Z2的形式.
根据X2+Y2=Z2的通解公式,




此时根据(5)z2=d2+a2可表示为

另一方面讨论勾股数组的规律.
根据前述X2+Y2=Z2的通解公式可知
从式中可以看出,当A、B确定后,勾股数组就可以确定,而且是唯一的.只有当A、B发生变化,勾股数组才相应发生变化.从中也说明一个勾股数组由三个整数所组成,当任意确定两个整数时,另一个整数也是唯一的.
按题意,需要求出该方程组的整数解,通过仔细研究该方程组可知,其实是构成两个直角三角形.式中a、d皆为正整数,那么y和z也应为正整数,那么就构成了两个勾股数组方程,在两个勾股数组方程中,都含有两个相同勾股数a和d.根据勾股数组可知,当已确定两个勾股数,另一个勾股数就应该是一定的,而且是唯一的,根据原方程x4+y4=z4,当x、y、z为非零整数解时,z>y,在此情形下,但在该方程组中,确出现了两个不同的勾股数组,这就说明,至少有一项是不能满足勾股数组的,也就是说,d2=y2+a2和z2=d2+a2两个方程组至少有一项不能为整数解,也说明z和y至少有一个不能为整数解.故此式x4+y4=z4无整数解.从证明的过程可知,该解法确实是很奇妙的,这也是我经过多次的研究后才得出的正确解法.综合以上的证明,原式x4+y4=z4的不定方程的任意整数时,没有不为零的整数解,这就是说:“不可能把一个整数的四次幂表示成两个整数的四次幂之和”.

几何解析为直观起见,我们也可以用几何图形来分析证明上述的结论.如图所示.
式中:直角三角形△ABC可表示成(x2)2+(y2)2=(z2)2,此时d2=y2+a2,z2=d2+a2,所以又可画出直角三角形△ADC和△ABE(x4+y4=z4几何关系图)
从直角三角形△ADC和△ABE中,分别构成两个勾股数组(、、)和(、、),在两个勾股数组中都含有两个相同的勾股数和,根据勾股数组可知,当已确定两个勾股数,另一个勾股数就应该是一定的,而且是唯一的,若满足勾股数组,只有,当时,根据通解公式,只有,显然不符合原式没有非零整数解的条件,根据原式的条件,,这此情形下,又不能满足勾股数组的条件,所以在两个勾股数组方程中,至少有一个方程不能满足是勾股数组的条件的,从而得出上述的结论.
评论从证明的过程可知,无论是论证的过程还是用几何图形的分析,该解法确实是很奇妙的,很长一段时间以来,通过运算的方式都没有证明结果,忽然有一天产生灵感而恍然大悟.现在想起来,x4+y4=z4不定方程没有非零整数解的过程竟是如此之简单,原来如此.
据有关资料的考证,当年费尔马自称是求证了x4+y4=z4不定方程没有非零整数解的证明,但没有留下论证过程.我想,当年费尔马所说的绝妙方法可能就是指这种论证方法的(因为当年费尔马是从研究毕达哥拉斯定理时而想到的,这种证法正是运用了该定理和勾股数组理论的),之后,许多大数学家都求证过x4+y4=z4不定方程没有非零整数解,但都是采用高深的复变函数理论和深奥的数论知识而求证的.我想,这肯定不是费尔马当时宣称的求证方法,据考证,目前还没有出现相同的证明的方法,这种方法即简洁明了,又奇妙无比.它的奇妙之处在于,一般的情形下,人们对某个问题的求解或论证,其逻辑思维都是采用运算的方式,只是很难想到用在两个联立的直角三角形方程中采用毕达哥拉斯定理和勾股数组(整数解)判定法,该方法即不用复杂的计算,也不用高等的复变函数、数论、群论等现代数学知识理论,而只要仔细的分析和判断就可证明了(只要掌握毕达哥拉斯定理和勾股数组的关系就足够了).
三、以新视角求证当n=2t(t为大于1的自然数)时,不定方程xn+yn=zn没有不为零的整数解

当n=2t(t为大于1的自然数),


符合X2+Y2=Z2的形式,

因为当X2+Y2=Z2时,
X=2ad,
Y=d2-a2,
Z=d2+a2,



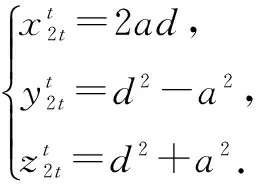

这时t又分两种情形,一种情形为t=2p,另一种情形为t=2p+1.
当t=2p时
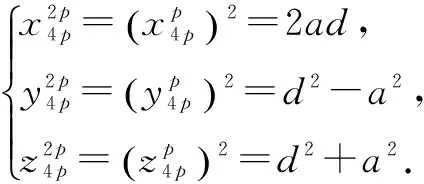
从上式中可以看出
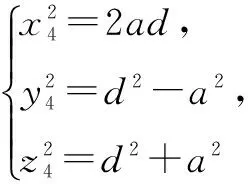
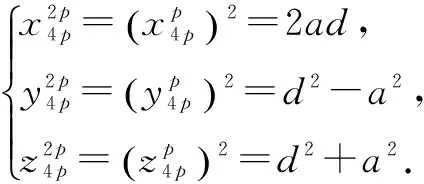
该式也无整数解,也说明当n=2t,t=2p,即n=4p时

当p为任意正整数时都无正整数解.
完全符合已证明的x4+y4=z4的形式.
当t=2p+1时,
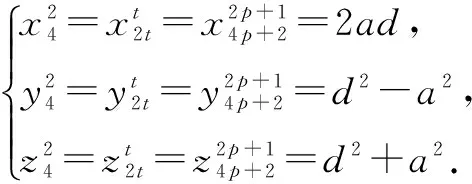
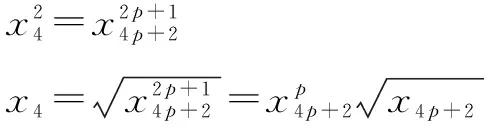
若该式有整数解,则x4p+2必为平方数,




根据前面的证明,该式无正整数解,也说明当n=2t,t=2p+1时,


四、以新视角求证当n=2t+1(t为自然数)时,不定方程xn+yn=zn没有不为零的整数解
当n=2t+1时(t为自然数时),


此时符合X2+Y2=Z2的形式,

因为当X2+Y2=Z2时,
所以

因ad皆为正整数,
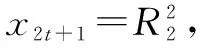
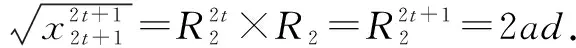


根据前式的证明,在该情形下,无正整数解.
几何解析同理,在一般的情形下,即当n=2t时,或n=2t+1(t为任意自然数)时,即当n>2时,

构成一个联立方程,所以,也可以用几何图形来分析证明上述的结论:如图所示(当n>2时).
式中:直角三角形△ABC可表示成
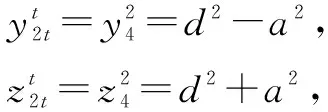
所以可写成d2=y2+a2,
(当n>2时的几何关系图)z2=d2+a2.
所以又可画出直角三角形△ADC和△ABE,同x4+y4=z4的证明过程一样(证明从略).
当n=2时,因只有关系式X2+Y2=Z2,所以几何图形为:

即上述证明的通解.
评论回顾上述的结论,就验证了当年费尔马所得出的结论.我认为事实上,当年费尔马也是按上述的逻辑关系而推论的,也没有求当n>2(除n=4)以外
的不定方程的解,也没有这个必要.因为根据推论已经属于普遍性的结论,是非常准确的.
三百多年来,人们都热衷于求证该不定方程,不仅仅是因为它有着诱人的一面,还因为它题目的本身是属于初等数学的范畴,多年未解出的原因是证明的思路不正确,把问题想的复杂化了(如x4+y4=z4没有非零整数解的证明,从上述的证明过程来看,只运用了毕达哥拉斯定理和勾股数组的概念,非常简单明了,没有必要用复杂的复变函数和数论进行求证),同时也忽略了幂与幂之间的联立关系,如果不考虑幂与幂之间的联立关系,而单纯的求解n>2的任意正整数时的不定方程,那将是难上加难,而用初等数学和高等数学那将是无法求解的.这就好比一个问题一旦被蒙上神秘的面纱,就无法看清它的真面目一样.如果一旦揭开它的面纱,又使人豁然开朗一样,我想该不定方程就属于这类性质,多年以来,我坚信当年费尔马一定是用初等数学方面的知识而求证的,当然不会用群论(那时还没有群论的概念),等现代数学理论而求证.只是方法很巧妙而已.通过上述的求证过程来看,不论是n=4时的求证,或是n为大于2的任意正整数时的求证和推演过程确实很巧妙,很奇妙,也很严谨.
综合以上的证明结果,这就证明了“费尔马(Fenmat)大定理”.即:不可能把一个整数的立方表示成两个整数的立方和,也不可能把一个整数的四次幂表示成两个整数的四次幂之和,这也就是说不定方程xn+yn=zn在n大于2的任意整数时,没有不为零的整数解.
通过以上的证明过程可以看出,从n=4时没有非零整数解的证明,以至n为任意大于2的整数皆没有非零整数解的论证,都是采用初等代数的方法而求解求证的,非常符合费尔马当时的年代,据有关资料考证,当年费尔马也是从研究X2+Y2=Z2的整数解开始思考的,继而求证了x4+y4=z4无非零整数解,又推导出xn+yn=zn当n>2时没有非零整数的过程.而且非常巧妙,所谓的巧妙其实就是一个好方法.
多年以来,很多的数学家都在研究该费尔马大定理的求证,也取得了很大的进展,虽然如此,还没有找到一个普遍性的证明,至到1993年,这个数学难题才由英国数学家威利斯(Andrew Wiles)所解决,其实威利斯是利用二十世纪过去三十年来抽象数学发展的结果才加以证明的,显然不是当年费尔马的证明思路,至此我们应该寻求当年费尔马的证明.
近期,在网上查阅了大量的各式各样的关于费尔马大定理的证明方法和证明过程.从证明的过程来看,有初等的,也有用复变函数的,有用无穷递降法的,也有用数论、群论的,但都不是费尔马当年证明的方法.不论是正确或错误,从解题的过程来看,一是不符合费尔马的时代背景,二是没有看到奇妙之处.我想,证明费尔马大定理的意义在于,一是要求证费尔马大定理的正确性,二是要符合费尔马的年代和费尔马的思维逻辑,与费尔马所论证的奇妙性相吻合.当年费尔马正是在研究毕达哥拉斯定理的整数解问题时,才有了费尔马大定理.事实上,从上述的证明过程看,从幂的四次方不定方程到幂的n次方不定方程都反复运用了毕达哥拉斯定理和勾股数组(整数解)的关系,真是对毕达哥拉斯定理的诠释和运用典范.这正是费尔马当年的绝妙的证明方法,可以对众多纷繁复杂的费尔马大定理的证明画上一个圆满的句号了,这也正是我多年寻求证明费尔马大定理的初衷.
参考文献:
[1]张文忠.数学撷英[M].北京:科学普及出版社,1983.
[2]A.B瓦西列夫斯基.数学解题教学法[M].长沙:湖南科学技术出版社,1982.
[3]夏圣亭.中学数学题巧解妙法[M].上海:上海科学普及出版社,1994.

