高效的多跳频信号2D-DOA估计算法
于欣永, 郭 英, 张坤峰, 眭 萍, 李 雷, 李红光, 孟 涛
(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 通信网信息传输与分发技术重点实验室,河北 石家庄 050081; 3. 空军通信士官学校, 辽宁 大连 116100)
0 引 言
跳频通信因其保密性好、抗干扰能力强、组网能力强等特点,广泛应用于航空航天通信领域,如Link16、美军军事卫星等,同时也向通信侦察提出了严峻的考验[1-3]。网台分选是跳频信号侦查的一个关键环节,它可以从复杂的电磁环境中将不同跳频电台分选出来,实现敌我识别,对敌方重要的通信电台实施跟踪、干扰、打击、破坏,为军事通信对抗情报生成、干扰引导及长期情报侦查提供依据和支撑。
针对跳频信号的侦查处理目前大多侧重于信号检测和时频域的参数估计,而对跳频信号的空域信息研究较少[4-6]。而跳频信号的空域信息如波达方向等在网台分选、信号跟踪和干扰中具有重要作用。文献[7-8]利用构造空时频模型进行跳频信号的波达方向(direction of arrival,DOA)估计,但是文中算法只能适用于超定情况,而实际复杂电磁环境中,大多情况处于欠定条件下;文献[9]运用空时频方法进行线性调频信号DOA估计及信号分离,取得了良好的效果,但是只适用于线性调频信号;文献[10]结合空时频模型和多重信号分类(multiple signal classification,MUSIC)算法进行跳频信号DOA估计,为跳频信号DOA估计提出了新的思路,这种方法可以适用于适定与欠定条件,估计精度较理想,但是算法复杂度高;文献[11-12]用root-MUSIC算法代替了文献[10]中的MUSIC算法,降低了计算复杂度,但是文中算法对阵列结构要求苛刻,实际工程应用中难以满足条件。文献[7-12]所提算法都只是关注的一维DOA信息,没有考虑二维DOA(two dimensional-DOA,2D-DOA)问题,无法定位三维的空间目标。针对跳频信号的2D-DOA估计问题,现有的研究较少,文献[13-14]将空间极化时频分布思想引入到跳频信号参数估计中,并结合旋转不变子空间(estimation of signal parameters via rotation invariant technique,ESPRIT)算法实现跳频信号的2D-DOA估计,可以在平行线阵和“L型”线阵下高精度估计出多跳频信号二维波达方向,但是这种算法要求信噪比高,而且ESPRIT需要进行参数配对,增加了计算量,降低了算法的估计性能。文献[15-16]提出了一种MUSIC对称压缩谱(MUSIC symmetrical compressed spectrum,MSCS)算法估计连续信号波达方向算法,这种算法在MUSIC算法基础上减少了谱峰搜索的次数,算法复杂度较小,但是只适用于连续信号。
为了利用跳频信号的空2D-DOA信息辅助多跳频信号的网台分选,本文提出一种空时频分析与MSCS相结合的多跳频信号2D-DOA估计的算法。首先在时频图上提取跳频信号的自相时频点,构造每个hop的空时频矩阵(spatial time-frequency distribution,STFD),进而得到时频域的协方差矩阵;然后将共轭子空间的思想引入到传统MUSIC算法中,通过对噪声子空间及其共轭的交集进行奇异值分解,实现噪声子空间的降维,进而构造新的降维空间谱函数;最终根据新的降维空间谱,只需在半谱内峰值搜索,实现跳频信号的2D-DOA估计。最后,对估计出来的2D-DOA信息进行聚类实现跳频信号的网台分选。另外,本文在时频图处理时采用形态学滤波进行去噪,提高了算法在低信噪比时的鲁棒性。仿真实验表明所提算法与MUSIC算法相比,在保证估计性能的同时将计算复杂度降低了一半。
1 跳频信号的阵列快拍模型
假设,在观测时间Δt内共有K个跳频信号sn(t),其跳周期为Tn,第k跳的载频、初相为ωnk、φnk,起始跳的时长为Δt0n,则sn(t)的表达形式[17]为
(1)
式中,t′=t-(k-1)Tn-Δt0n;υn是信号sn(t)的基带复包络;rect表示单位矩形脉冲。
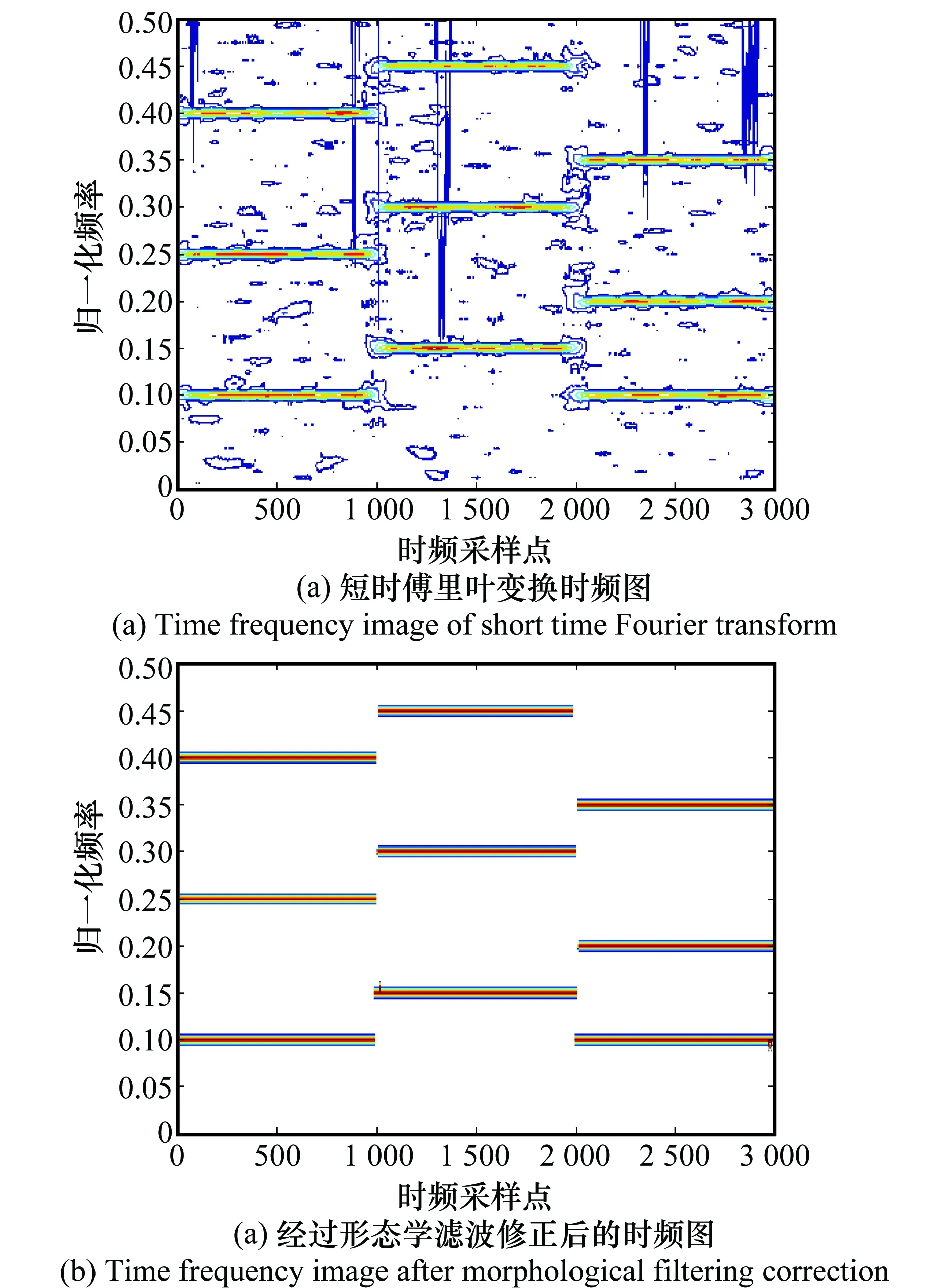
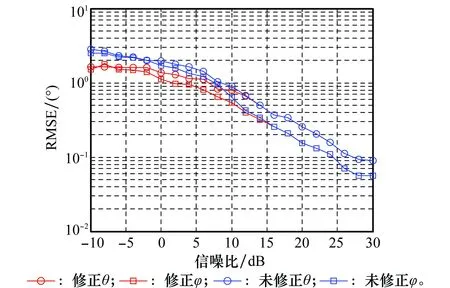
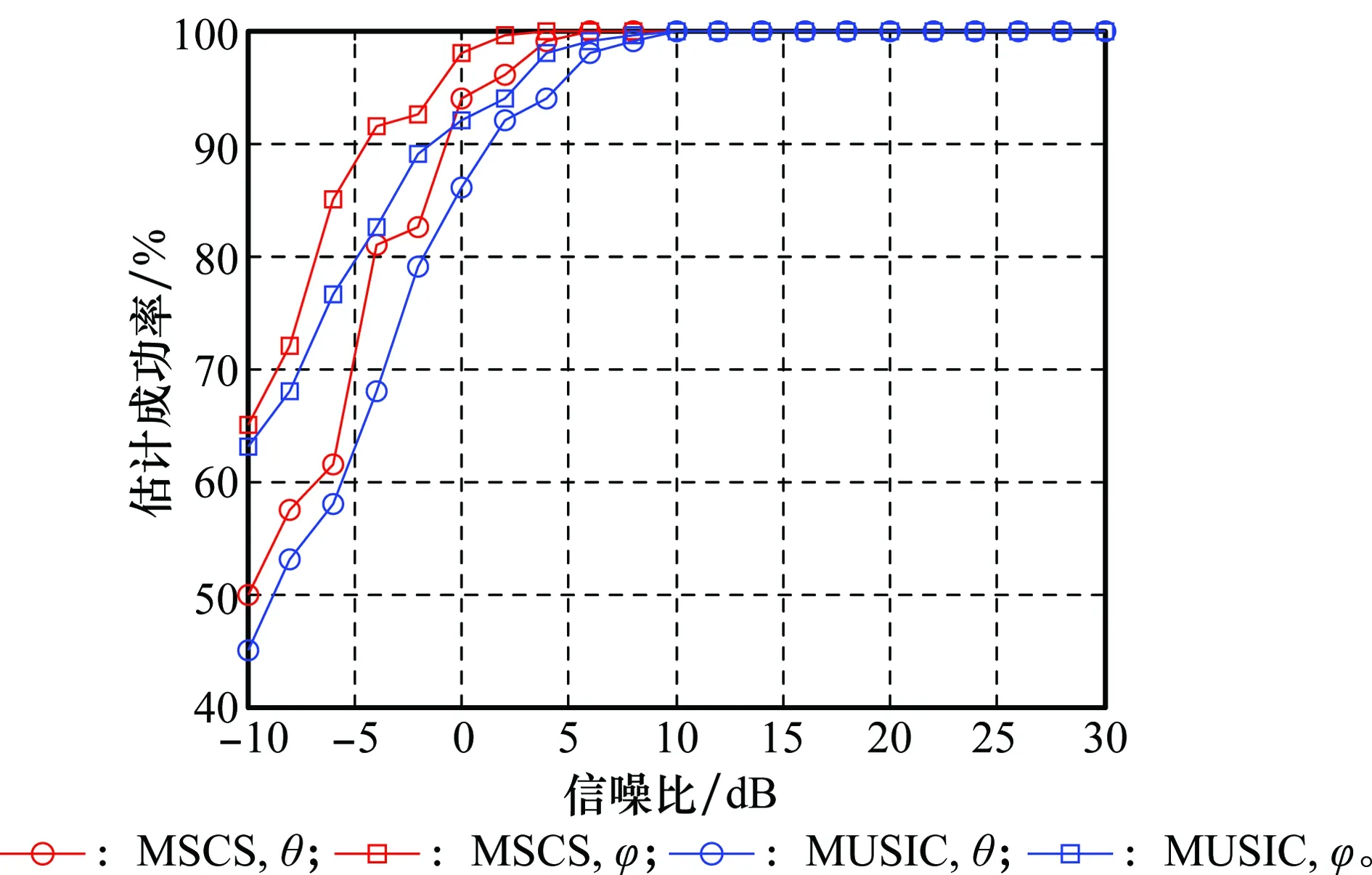
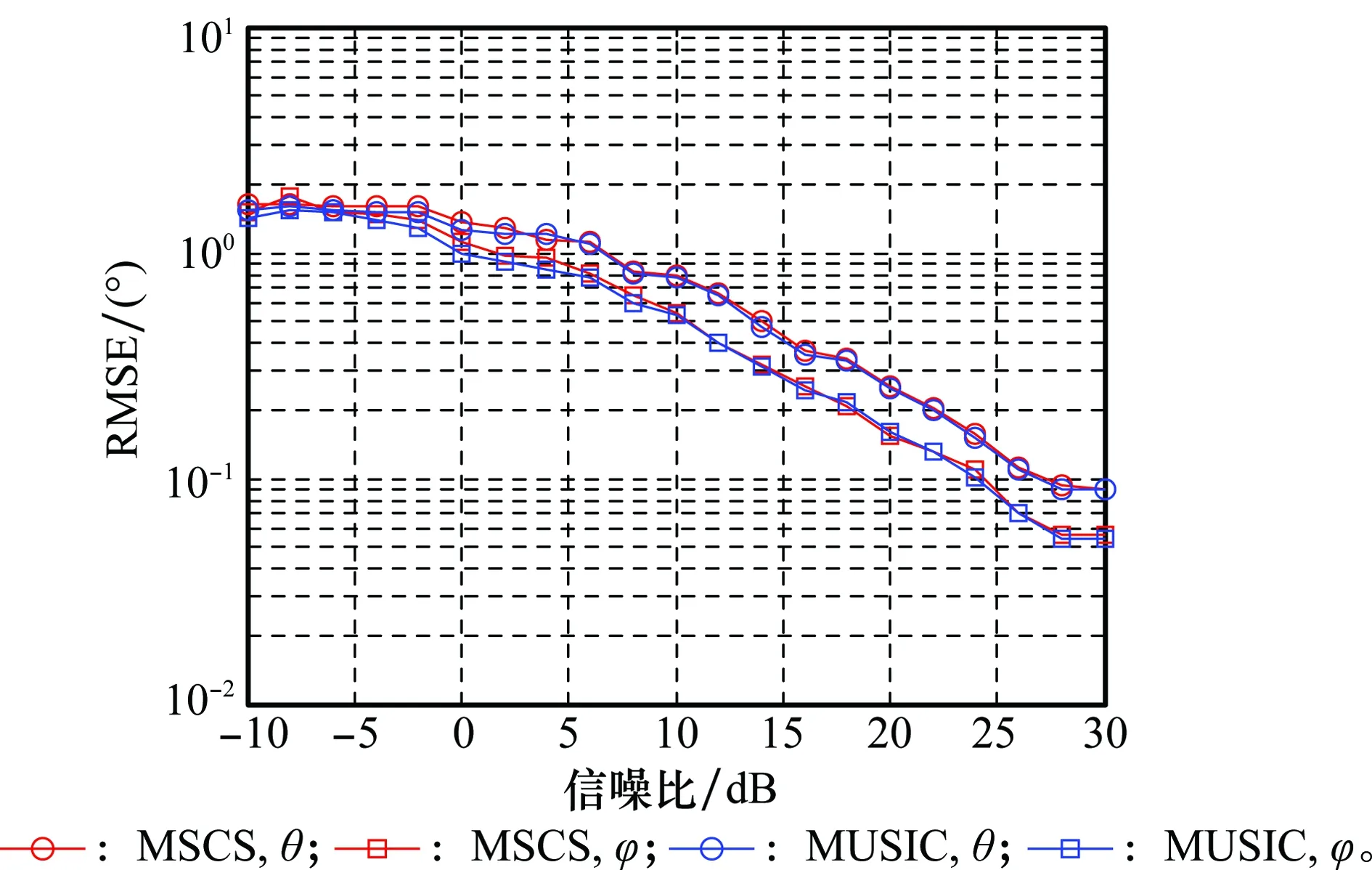
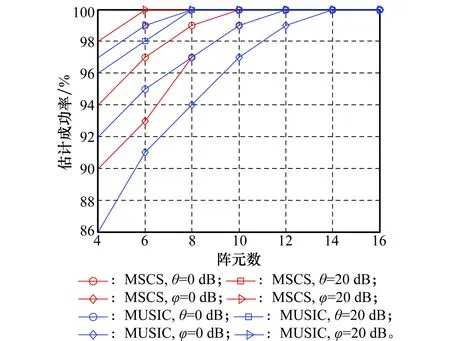
假设N个跳频信号被如图1所示的阵列接收,图中两均匀线阵(uniform linear array, ULA)ULA1、ULA2的阵元数为M,阵元间距为d1,阵列的间距为d2,且满足max(d1,d2) 图1 双平行均匀线阵Fig.1 Double parallel uniform linear array 跳频信号的载频随着伪随机码随机跳变,是一个宽带信号,但是只分析某一跳时,可以当作分段窄带信号进行处理。假设跳频信号S以方位角θ∈[0,2π]和俯仰角φ∈[0,π/2]从远场入射到接收阵列上。阵元增益为1,则子阵ULA1对入射波S的导向矢量aS1(θ,φ)为 aS1(θ,φ) =[1,e-j2πd1sin θcos φ/λ,…,e-j2π(M-1)d1sin θcos φ/λ]T (2) 式中,λ为信号的波长。ULA2对入射波S的导向矢量为aS2(θ,φ),相比较aS1(θ,φ)差别是由阵列距离d2引起,则aS2(θ,φ)为 aS2(θ,φ) =[1,e-j2π(d1sin θcos φ+d2sin θsin φ)/λ,…, e-j2π[(M-1)d1sin θcos φ+d2sin θsin φ]/λ]T (3) 则阵列对入射波S的导向矢量a(θ,φ)为 (4) 由导向矢量组成的阵列流型矩阵为 A=[a1(θ,φ),a2(θ,φ),…,aN(θ,φ)] (5) 则跳频信号的阵列快拍模型为 X(t)=Y(t)+N(t)=AS(t)+N(t) (6) 式中,X(t)=[x1(t),x2(t),…,xM(t)]T为阵列接收到的数据矢量;S(t)=[s1(t),s2(t),…,sN(t)]T为跳频信源数据矢量;N(t)=[n1(t),n2(t),…,nM(t)]T为噪声数据矢量。 信号xi(t)的Cohen类离散时频分布为 (7) 式中,φ(l,τ)为核函数。信号xi(t)与xj(t)离散形式的Cohen类互时频分布为 (8) 定义信号x(t)的空时频分布为 (9) 式中,[DXX(t,f)]ij=Dxixj(t,f)表示各阵列输出信号之间的互时频分布。根据式(6)和式(9)得到接收阵列的时频域协方差矩阵为 E[DXX(t,f)]=E[DYY(t,f)]+E[DNN(t,f)]= ADSS(t,f)AH+E[DNN(t,f)] (10) 选取自项时频点构造STFD是2D-DOA估计性能的前提,特别在低信噪比情况下,短时傅里叶变换得到的时频图效果不佳。本文利用形态学滤波的方法对时频图进行修正,在修正的时频图上完成各个hop的提取。 假设时频图上任意一时频点频率的模值为F(t,f)∈[Fmin(t,f),Fmax(t,f)],对短时傅里叶变换得到的跳频信号时频图做阈值分割处理转化为二值图像,处理后的时频图矩阵为 (11) 本文阈值ε通过自适应信噪比迭代算法来确定,算法流程如下。 步骤1假设初始阈值为ε0=[Fmin(t,f)+Fmax(t,f)]/2; 步骤2按照式(11)用ε0截取短时傅里叶得到的时频图,把时频图划分为两个部分; 步骤3对划分后的两部分分别计算其平均频率模值,并取其和的一半作为新的阈值ε1; 步骤4用ε1按照式(11)重新进行截取,按照步骤3一直迭代至第N+1次的阈值与第N次的阈值相等,即该阈值为最佳分割阈值ε。 fΘB=min{f(x-x′,y-y′)-b(x′,y′)|(x′,y′)∈Db} (12) f⊕B=max{f(x-x′,y-y′)+ b(x′,y′)|(x′,y′)∈Db} (13) 式中,b(x′,y′)为结构元素;Db为b(x′,y′)的定义域。腐蚀能够消除影响对某一跳提取的散点,同时会使边界收缩;膨胀可以填补信号中的空洞,而且会将边界扩张。因此,通过腐蚀和膨胀处理可以消除时频图中的干扰噪声点以及散点而对图像中的其他点没有影响,进而得到一个清晰稳健的时频图,再通过坐标变换将该时频图从二值图像转换为原始图像。 图2(a)、图2(b)分别为3个同步跳频信号在信噪比为-5 dB下只经过短时傅里叶变换的时频图和采用形态学滤波修正之后的时频图。可见,短时傅里叶变换得到的时频图背景噪声大,时频聚焦性差;采用形态学滤波去噪之后的时频图能量更集中,更有利于自相时频点的提取。 图2 多跳频信号时频分布图Fig.2 Time frequency distribution of multi-frequency-hopping signals 假设阵列同时接收到跳频信号的个数为L,则时频域协方差矩阵E[DXX(t,f)]经过特征值分解可表示为 (14) 式中,US表示信号子空间;UN表示噪声子空间;Σ为E[DXX(t,f)]特征值组成的对角矩阵。由噪声子空间UN构造的MUSIC算法空间谱函数PMUSIC(θ,φ)为 (15) 根据PMUSIC(θ,φ)在(θ,φ)二维域进行谱峰搜索,使得PMUSIC(θ,φ)取得极值的(θ,φ)即为所求2D-DOA,由于传统MUSIC算法需在全场范围内进行谱峰搜索,使得算法复杂度过高。 (16) 对式(2)和式(3)的导向矢量两端取共轭可得 (17) (18) 由式(17)和式(18)可得 (19) 对式(16)两端取共轭,利用式(19)得 (20) (21) 由式(21)可知,当φ∈[0,π],有 (22) 同理可得,当φ∈[π,2π]时,有 PMSCS(θ,φ-π)=PMSCS(θ,φ) (23) 令噪声子空间UN=[UN1,UN2,…,UNM-L],则 (24) 将式(24)代入式(21)并取倒数可得 (25) 由式(16)和式(25)可得 (26) 对R进行奇异值分解得 R=UΛVH (27) 式中,Λ为对角阵,则 (28) (29) 基于以上分析论述,本文所提的基于MSCS的多跳频信号2D-DOA估计算法具体步骤如下。 步骤1根据式(11)采用自适应信噪比作为阈值对短时傅里叶得到的跳频信号时频图二值化处理,然后用式(12)、式(13)对处理后的图像进行形态学滤波修正,得到清晰稳健的时频图; 步骤2在修正后的时频图上提取每个hop的自项时频点根据式(9)构建STFD,并根据式(10)求得其时频域的协方差矩阵; 步骤5根据式(29)构建MSCS空间谱函数,在(θ,φ)二维域进行半谱峰搜索,完成2D-DOA的高效估计。 假设根据空间谱函数进行谱峰搜索时,搜索步长为ζ,在MUSIC算法中,根据式(15)构造空间谱函数时算法的复杂度为3M2-2ML,则MUSIC算法估计多跳频信号2D-DOA的计算量G为 G=π(3M2-2ML)/ζ (30) (31) (32) 可以看出,在进行跳频信号2D-DOA估计时,相比较MUSIC算法,MSCS的算法复杂度降低一半左右。 假设ULA1、ULA2的阵元间距d1为2.5 m,阵列的间距d2为3 m;空间中存在5个跳频信号FH1~FH5的二维DOA参数(θ,φ)分别为(20°,30°),(40°,50°),(60°,70°),(70°,60°),(80°,40°);跳周期均为10 μs,归一化载频在0~0.5随机跳变,采样率为100 MHz。 实验2~实验5均为经过形态学滤波处理的条件下做的仿真,每次实验进行200次蒙特卡罗计算,选用均方根误差(root mean square error, RMSE)和估计成功率作为衡量算法性能好坏的标准。RMSE的定义为 (33) η=N1/N (34) 式中,N1代表200次蒙特卡罗实验中方位角(俯仰角)估计误差小于2°的实验次数,N代表总实验次数,即N=200。 为了验证形态学滤波对本文所提算法进行跳频信号2D-DOA估计性能的影响,假设阵列同时接收到的3个跳频信号FH1、FH2和FH3,各跳的快拍数为2 000,阵列ULA1和ULA2的阵元数均为4,信噪比以2 dB为步进从-10 dB递增到30 dB,有无经过形态学滤波修正的MSCS算法估计性能如图3和图4所示。 图3 实验1参数估计成功率Fig.3 Estimated success rate of parameters in experiment 1 图4 实验1参数的RMSEFig.4 RMSE of parameters in experiment 1 实验1的结果表明,不管有无经过形态学滤波处理,MSCS算法方位角及俯仰角的估计成功率都随着信噪比的增加而逐渐增大,RMSE都随着信噪比的增加而逐渐减小;当信噪比小于10 dB时,经形态学滤波处理的估计成功率和RMSE均优于未经形态学滤波处理的算法;当信噪比大于10 dB时,两种情况估计性能相当。 假设空间中存在3个跳频信号FH1、FH2和FH3,各跳的快拍数为2 000,ULA1和ULA2的阵元数均为4,信噪比以2 dB为步进从-10 dB递增到30 dB,MSCS算法和MUSIC算法的2D-DOA估计性能曲线如图5和图6所示。 实验2的结果表明,两种算法对跳频信号的方位角及俯仰角的估计成功率随着信噪比的增加而逐渐增大,而RMSE随着信噪比的增加而逐渐减小;当信噪比达到10 dB左右时,两种算法的参数估计成功率均达到100%;整体上MSCS算法的估计成功率要略高于MUSIC算法;信噪比在-10~10 dB时,MSCS算法的估计精度要略差于MUSIC算法,但是当信噪比大于10 dB时两种算法的估计精度相当。 图5 实验2参数估计成功率Fig.5 Estimated success rate of parameters in experiment 2 图6 实验2参数的RMSEFig.6 RMSE of parameters in experiment 2 为了验证阵元数对算法的影响,假设空间中存在3个跳频信号分别FH1、FH2和FH3,各跳的快拍数为2 000,ULA1、ULA2的阵元数以2为步进从4递增到16,在信噪比分别0 dB和20 dB时,MSCS算法和MUSIC算法的估计性能如图7和图8所示。 图7 实验3参数估计成功率Fig.7 Estimated success rate of parameters in experiment 3 图8 实验3参数的RMSEFig.8 RMSE of parameters in experiment 3 实验3的结果表明,两种算法的估计成功率都随着阵元数的增加而增加,RMSE随之减小;在相同的信噪比下,MSCS算法参数估计成功率要高于MUSIC算法;阵元数大于10时,MSCS算法的整体估计精度要略低于MUSIC算法,阵元数小于10时,两种算法估计精度相当。造成这样现象是由于随着阵元数的增加,MSCS噪声子空间维度下降而使得空间谱变得更加的“尖锐”。 为了验证快拍数对算法性能的影响,假设空间中的3个跳频信号分别为FH1、FH2和FH3,ULA1、ULA2的阵元数是4,各跳的快拍数从1 000递增到3 000,在信噪比分别为0 dB和20 dB时,MSCS算法和MUSIC算法的估计性能如图9和图10所示。 图9 实验4参数估计成功率Fig.9 Estimated success rate of parameters in experiment 4 实验4的结果表明,两种算法的DOA估计性能都随着快拍数的增加而变优;在相同的信噪比下,MSCS算法的估计成功率总体上要略高于MUSIC算法;但是相同快拍数下MSCS算法的估计精度要略低于MUSIC算法。 图10 实验4参数的RMSEFig.10 RMSE of parameters in experiment 4 为了验证MSCS算法相对于MUSIC算法在复杂度上的优势,假设空间中5个跳频信号FH1~FH5全部存在,各跳快拍数为3 000,信噪比以4 dB为步进从-8 dB递增到20 dB时,两种算法2D-DOA估计所需的时间如表1所示。 表3 2D-DOA估计所需时间 实验5的结果表明,在不同的信噪比下,MSCS算法2D-DOA估计的时间约为MUSIC算法的估计时间的一半左右;由此可见,相比较传统MUSIC算法,本文算法的复杂度降低了一半左右。 跳频信号的2D-DOA信息能够有效地辅助多跳频信号网台分选,多跳频信号的2D-DOA估计有着重要的意义。本文详细推导和阐述了基于空时频分析与MSCS算法相结合的多跳频信号2D-DOA高效估计算法,为了提高所提算法在低信噪比下的鲁棒性,将形态学滤波的思想引入到时频图处理中。理论论证和实验仿真表明,与传统MUSIC算法相比,本文所提算法在保证估计性能的同时将算法复杂度降低了一半左右。 参考文献: [1] SHA Z C. Online hop timing detection and frequency estimation of multiple FH signals[J]. Etri Journal, 2013, 35(5):748-756. [2] IBRAHIM M, GALAL I. An improved SDR frequency tuning algorithm for frequency hopping systems[J]. Etri Journal, 2016,8(3):89-105. [3] HANAWAL M, ABDELRAHMAN M, KRUNZ M. Joint adaptation of frequency hopping and transmission rate for anti-jamming wireless systems[J]. IEEE Trans.on Mobile Computing, 2016, 15(9):2247-2259. [4] 赵新明,金艳,姬红兵.a稳定分布噪声下基于Merid滤波的跳频信号参数估计[J].电子与信息学报,2014,36(8):1878-1883. ZHAOX M, JIN Y, JI H B. Parameter estimation of frequency-hopping signals based on Merid filter in a stable noise environment[J]. Journal of Electronics &Information Technology, 2014, 36(8):1878-1883. [5] 张坤峰,郭英,齐子森,等.基于稀疏贝叶斯重构的多跳频信号参数估计[J].华中科技大学学报:自然科学版,2017,45(1):97-102. ZHANG K F, GUO Y, QI Z S,et al. Parameter estimation for multiple frequency-hopping signals based on sparse Bayesian reconstruction[J]. Journal of Huazhong University of Science and Technology, 2017,45(1):97-102. [6] FU K C, CHEN Y F. Blind iterative maximum likelihood-based frequency and transition time estimation for frequency hopping systems[J]. IET Communications, 2013, 7(9):883-892. [7] LIN C H, FANG W H. Joint angle and delay estimation in frequency hopping systems[J]. IEEE Trans.on Aerospace & Electronic Systems, 2013, 49(2):1042-1056. [8] LIU X, LI J, MA X. An EM algorithm for blind hop timing estimation of multiple FH signals using an array system with bandwidth mismatch[J]. 2007, 56(5):2545-2554. [9] ZHANG Y, MA W, AMIN M G. Subspace analysis of spatial time-frequency distribution matrices[J]. IEEE Trans.on Signal Processing, 2001, 49(4):747-759. [10] 陈利虎, 王永明, 张尔扬. 基于空时频分析的多FH/DS信号DOA估计[J]. 信号处理, 2009, 25(8):1309-1313. CHEN L H, WANG Y M, ZHANG E Y. Directions of arrival estimation for multicomponent frequency-hopping/direct sequence spread spectrum signal based on spatial time-frequency analysis[J]. Signal Processing, 2009, 25(8):1309-1313. [11] ZHANG C, LI L. Parameter estimation of multi frequency hopping signals based on compressive spatial time-frequency joint analysis[J]. Pacific Journal of Mathematics, 2014, 136(1): 85-101. [12] 张东伟, 郭英, 齐子森,等. 多跳频信号波达方向与极化状态联合估计算法[J]. 电子与信息学报, 2015,37(7):1695-1701. ZHANG D W, GUO Y, QI Z S, et al. Joint estimation algorithm of direction of arrival and polarization for multiple frequency hopping signals[J]. Journal of Electronics and Information Technology, 2015,37(7):1695-1701. [13] 张东伟,郭英,张坤峰,等.多跳频信号频率跟踪与二维波达方向实时估计算法[J].电子与信息学报,2016,38(9):2377-2384. ZHANG D W, GUO Y, ZHANG K F, et al. Online estimation algorithm of 2D-DOA and frequency tracking for multiple frequency-hopping signals[J]. Journal of Electronics & Information Technology, 2016, 38(9): 2377-2384. [14] 张东伟, 郭英, 齐子森, 等. 跳频信号2D-DOA与极化参数的欠定估计[J]. 哈尔滨工业大学学报, 2016, 48(4):121-128. ZHANG D W, GUO Y, QI Z S, et al. Underdetermined estimation of 2D-DOA and polarization for frequencyhopping signals[J].Journal of Harbin Institute of Technology,2016,48(4):121-128. [15] 闫锋刚,刘帅,金铭,等.基于MUSIC对称压缩谱的快速DOA估计[J].系统工程与电子技术,2012,34(11):2198-2202. YAN F G, LIU S, JIN M, et al. Fast DOA estimation based on MUSIC symmetrical compressed spectrum[J]. System Engineering and Electronics, 2012, 34(11):2198-2202. [16] 闫锋刚, 刘帅, 金铭, 等. 基于降维噪声子空间的二维阵列DOA估计算法[J]. 电子与信息学报, 2012, 34(4):832-837. YAN F G, LIU S, JIN M, et al. 2-DDOA Estimation method based on dimension descended noise subspace[J]. Journal of Electronics & Information Technology, 2012, 34(4):832-837. [17] 冯永新,徐美荣,钱博,等.一种差分跳频频率转移函数算法[J].航空学报,2013,34(3):655-661. FENG Y X, XU M R, QIAN B, et al. A frequency transform function algorithm for differential frenquency hopping[J]. Chinese Journal of Aeronautics, 2013, 34(3):655-661.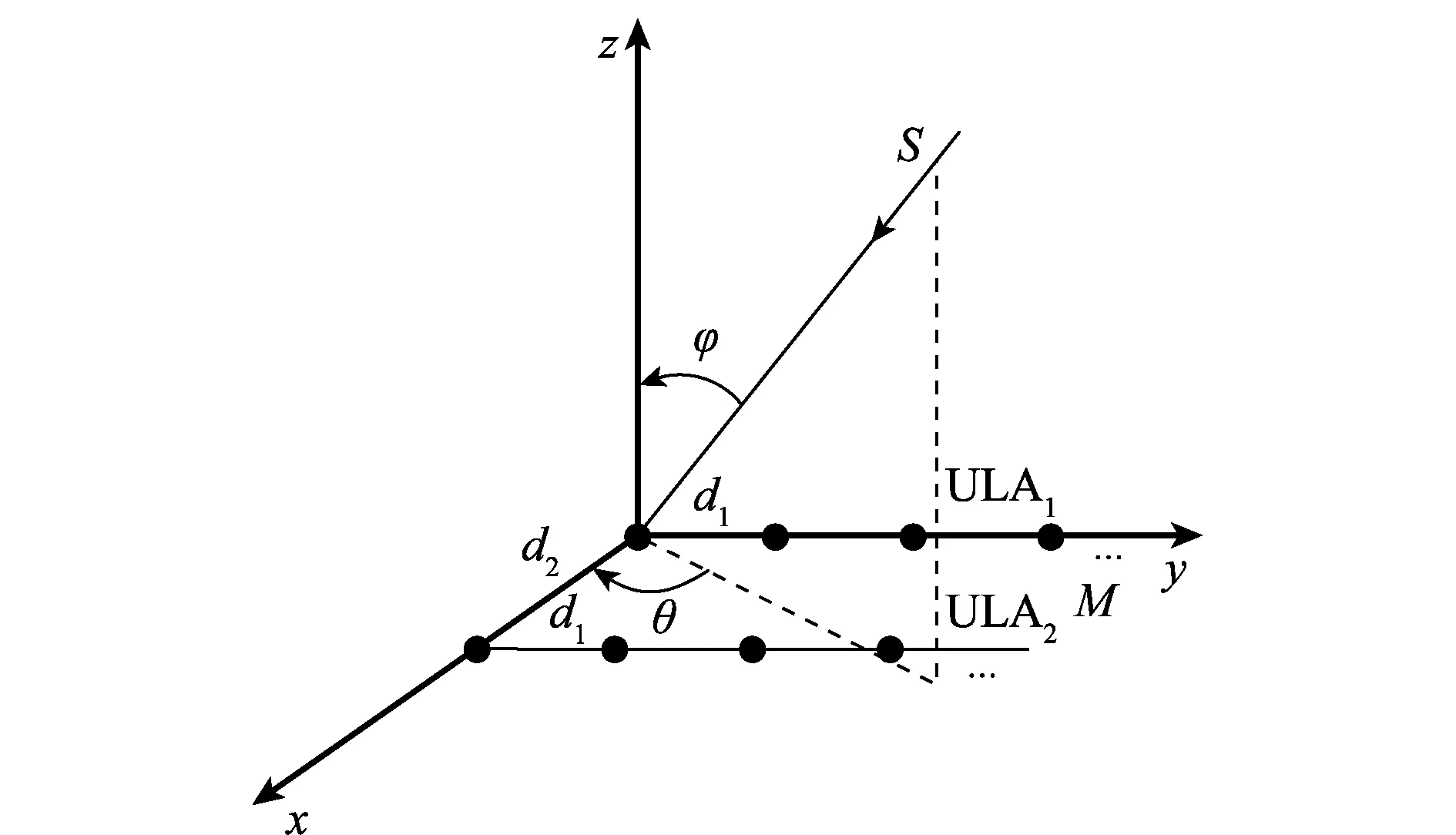
2 跳频信号STFD构造
2.1 STFD基本原理
2.2 高精度STFD构造

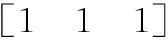
3 基于MSCS的2D-DOA估计
3.1 MUSIC算法原理
3.2 MSCS算法原理
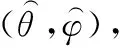
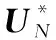
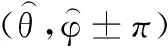
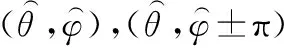
3.3 2D-DOA估计
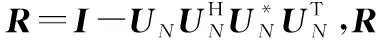
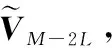
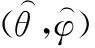
4 算法流程及复杂度分析
4.1 算法流程
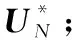
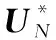
4.2 算法复杂度分析
5 仿真与分析
5.1 实验1
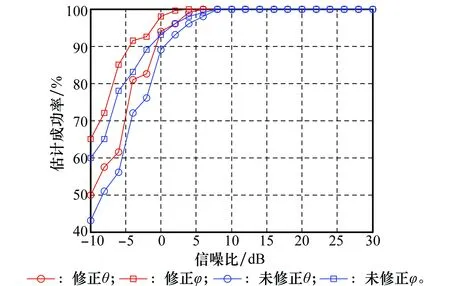
5.2 实验2
5.3 实验3
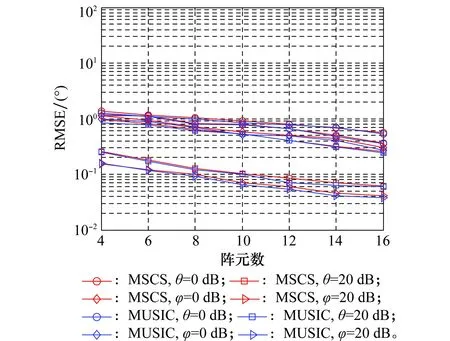
5.4 实验4
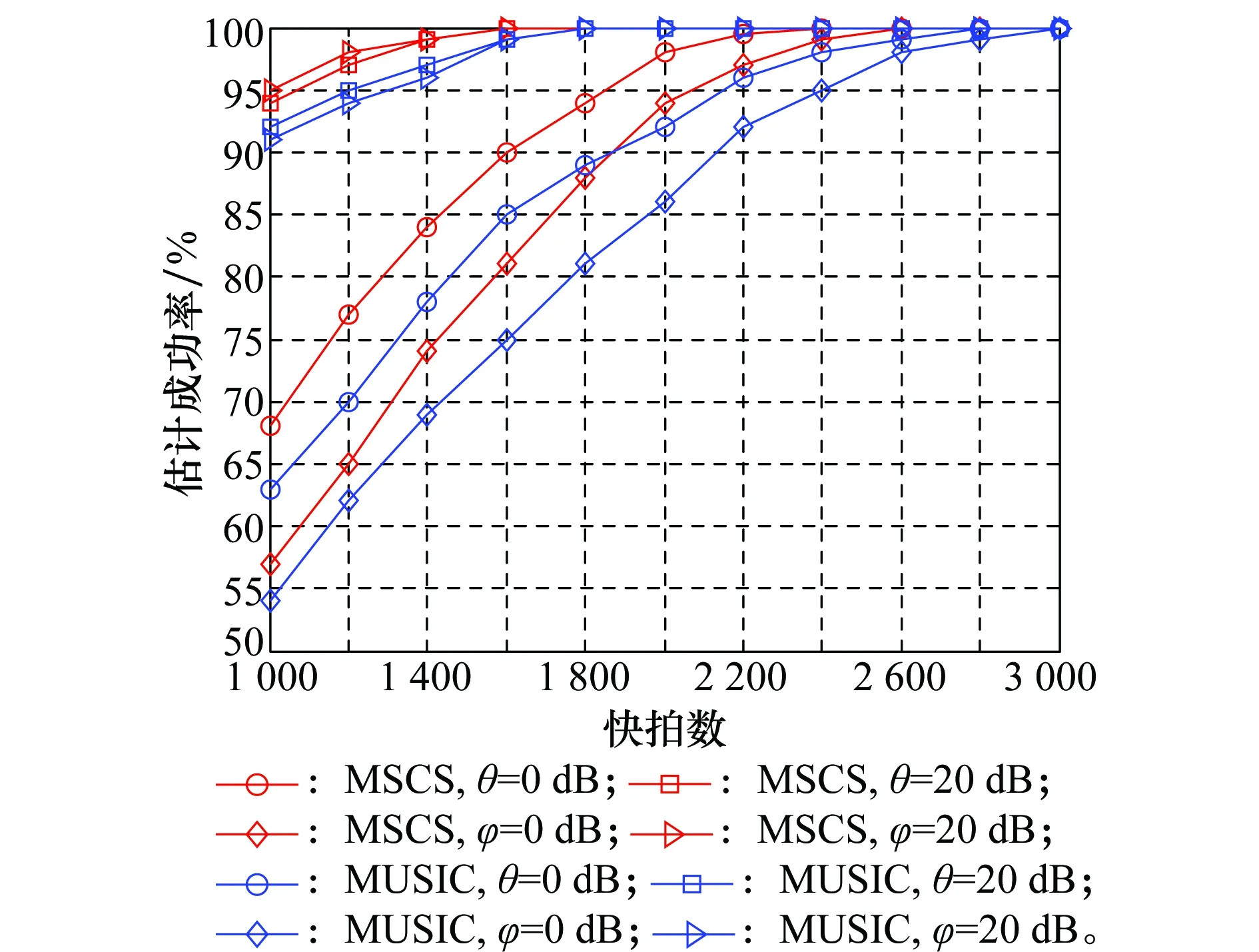
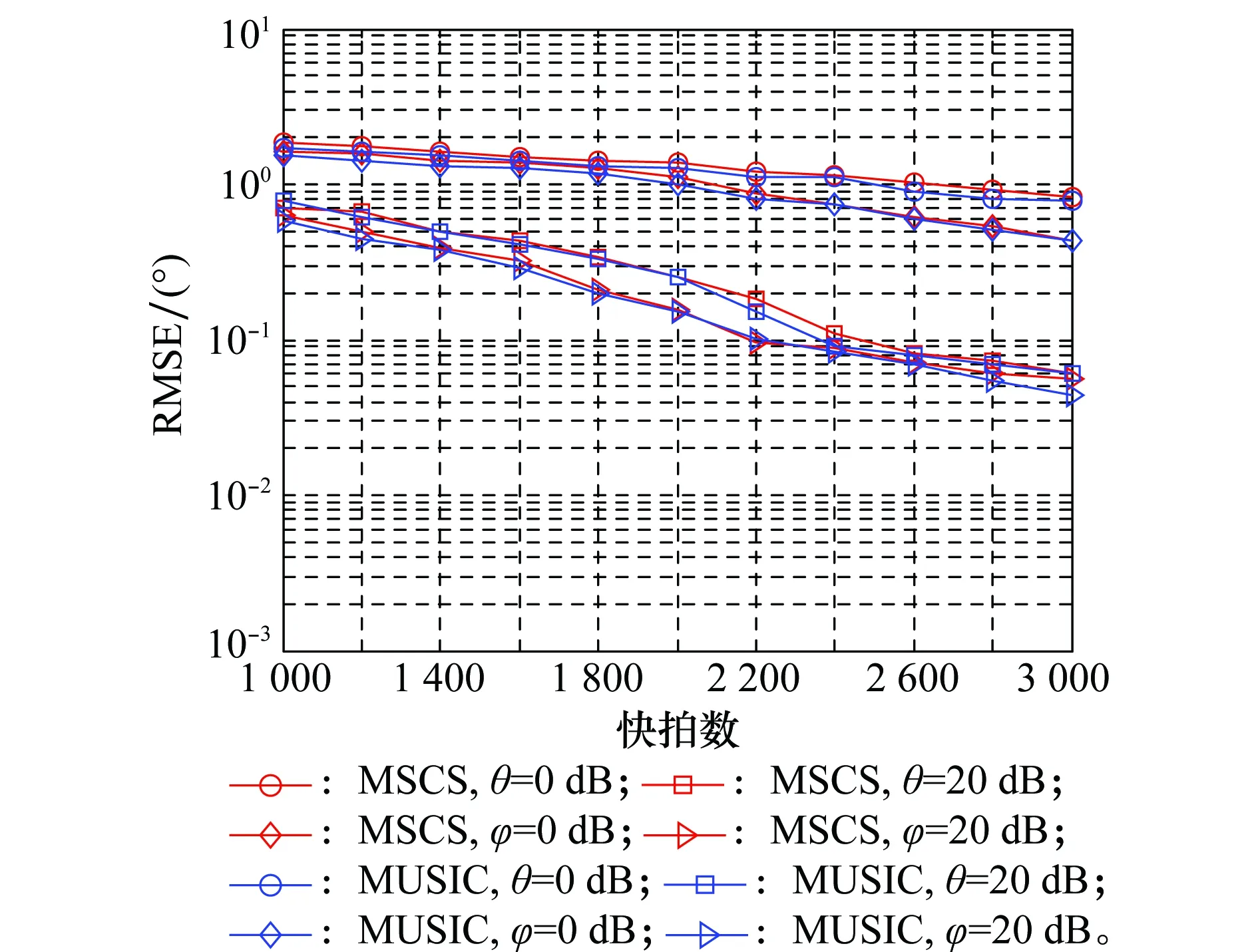
5.5 实验5
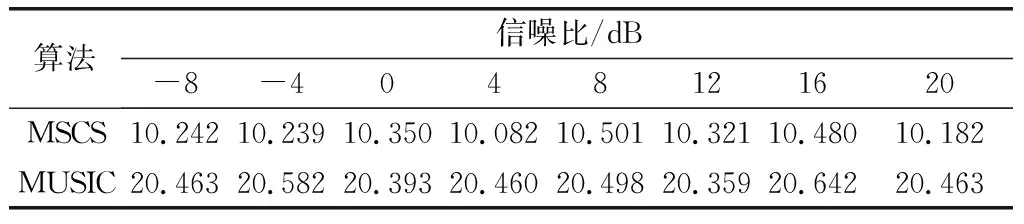
6 结 论

