Thermodynamic Nonequilibrium Features in Binary Diffusion∗

2018-06-15 07:32ChuanDongLin林传栋KaiHongLuo罗开红YanBiaoGan甘延标andHuiLinLai赖惠林

Communications in Theoretical Physics 2018年6期

Chuan-Dong Lin(林传栋)† Kai Hong Luo(罗开红)‡ Yan-Biao Gan(甘延标)and Hui-Lin Lai(赖惠林)

1Center for Combustion Energy,Key Laboratory for Thermal Science and Power Engineering of Ministry of Education,Department of Energy and Power Engineering,Tsinghua University,Beijing 100084,China

2College of Mathematics and Informatics&FJKLMAA,Fujian Normal University,Fuzhou 350007,China

3Department of Mechanical Engineering,University College London,Torrington Place,London WC1E 7JE,UK

4North China Institute of Aerospace Engineering,Langfang 065000,China

Diffusion is the net movement of particles down their concentration gradient.It takes place when miscible materials are brought together.[1]It is a fundamental and ubiquitous phenomenon in nature and widely exists in engineering,sciences,technologies and beyond.[1]For example,diffusion plays a key role in the storage and mining of shale gas,partially premixed or nonpremixed combustion,etc.Physically,diffusion is a typical scenario that incorporates various essential thermodynamic nonequilibrium effects(TNEs).Early in 1855,Fick’s laws of diffusion were presented in the background of thermodynamics and nonequilibrium thermodynamics.[1]Later,the theory of diffusion in gases was developed based on Boltzmann’s equation.[2]However,the nonlinear complexity and pronounced TNEs often provide challenges to previous theoretical studies.

In recent decades,researches into nonlinear complex systems have been significantly promoted by numerical approaches,such as the lattice Boltzmann method(LBM).[3−12]In 2004,Briant and Yeomans utilized the LBM to simulate the relative diffusion of two fluid components in the vicinity of the contact line.[4]In 2016,an LBM was developed for solving the fractional advection-diffusion equation.[9]However,previous LBMs were mainly used to solve hydrodynamic equations,but ignored some detained TNEs.As a variant of traditional LBMs,the discrete Boltzmann method(DBM)[13−17]has achieved great success in simulating nonequilibrium systems,such as multiphase flows, fluid instabilities,combustion,etc.Very recently,the TNEs in binary diffusion were demonstrated by a double-distribution-function DBM.[16]

In this work,we adopt the DBM to have a deeper probe into the nonequilibrium features of binary diffusion.The DBM is based on the following equation,[16]

Toconductnumericalsimulations,thetemporal derivative in Eq.(1)is calculated in its analytical form,[15]and the spatial derivative is solved by the second order non-oscillatory and non-free-parameter dissipation difference scheme.[19]Next,let us investigate the nonequilibrium effects in the binary diffusion.The initial con figuration is

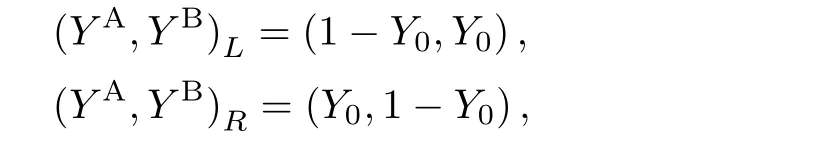
whereL(R)indicates the left(right)part of the computational domain,and(ρ,u,T)=(1,0,T0)in the two parts.YAandYBrepresent the mole fraction of species A and B,respectively.Furthermore,the in flow and periodic boundary conditions are adopted in thexandydirections,respectively.First of all,two cases of simulations are performed.In Case I,the initial temperature isT0=1,the mole fractionY0=5%,the relaxation timeτ=2×10−5,the time step ∆t=10−7,the space step∆x= ∆y=2×10−6,the meshNx=Ny=5000×1.In Case II,the parameters areT0=2,Y0=25%,τ=4×10−5,∆t=2×10−7,∆x= ∆y=4×10−6,Nx=Ny=2500×1.

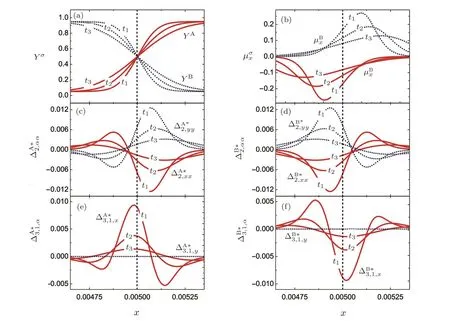
Fig.1 Physical quantities and TNE characterizations around the material interface at representative instants,t1=2× 10−4,t2=4× 10−4,and t3=8× 10−4,respectively.(a)Mole fraction Yσ,(b)horizontal velocity uσx,(c)nonorganised energy∆A∗2,αα,(d)nonorganised energy∆B∗2,αα,(e)nonorganised energy flux∆A∗3,1,α,and(f)nonorganised energy flux∆B∗3,1,α.In each plot,a vertical line is plotted at the material interface.

In fact,we can recover the main characteristics of the distribution functionfσfrom the above nonequilibrium in Fig.2(a),and the main feature offAin the velocity space(vx,vy)is shown in Fig.2(c).Similarly,the sketch offBis plotted in Figs.2(b)and 2(d).

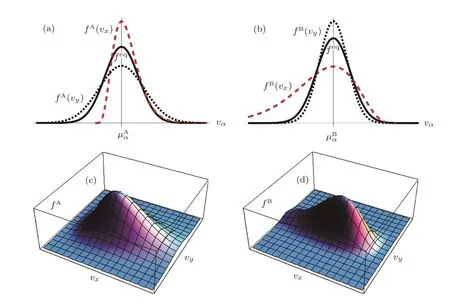
Fig.2 Sketches of the velocity distribution functions at the material interface:(a)fAversus vxor vy,(b)fB versus vxor vy,(c)fAin the velocity space(vx,vy),and(d)fBin the velocity space(vx,vy).

To investigate the dependence of the TNEs on the relaxation time,we carry out two groups of simulations.Group I hasT0=1 andY0=5%.Group II hasT0=2 andY0=25%.Considering both the accuracy and efficiency,we choose the time and space steps as(∆t,∆x)=(5×10−8,10−6),(10−7,2×10−6),(2×10−7,4×10−6),(4×10−7,8×10−6),(8×10−7,1.6×10−5)for simula-tions with relaxation timeτ=10−5,2×10−5,4×10−5,8×10−5,1.6×10−4,respectively.Figure 4 plots the relationship between the TNEs and the relaxation time att=0.002.The fitting functions areF(ϕ)=3.71+0.989ϕandF(ϕ)=2.29+1.50ϕin Fig.4(a),F(ϕ)=7.69+1.47ϕandF(ϕ)=6.12+1.97ϕin Fig.4(b),F(ϕ)=4.02+0.995ϕandF(ϕ)=2.83+1.50ϕin Fig.4(c),F(ϕ)=7.81+1.44ϕandF(ϕ)=6.66+1.95ϕin Fig.4(d),respectively,withϕ=ln(τ). It is clear that both the local and global TNEs increase with the relaxation time in a power-law form.Theoretically,the physical gradients reduce fast for large relaxation time.The reducing physical gradients and increasing relaxation time exert opposite effects on the TNEs,[16]but the latter dominates for parameter space considered in our simulations.

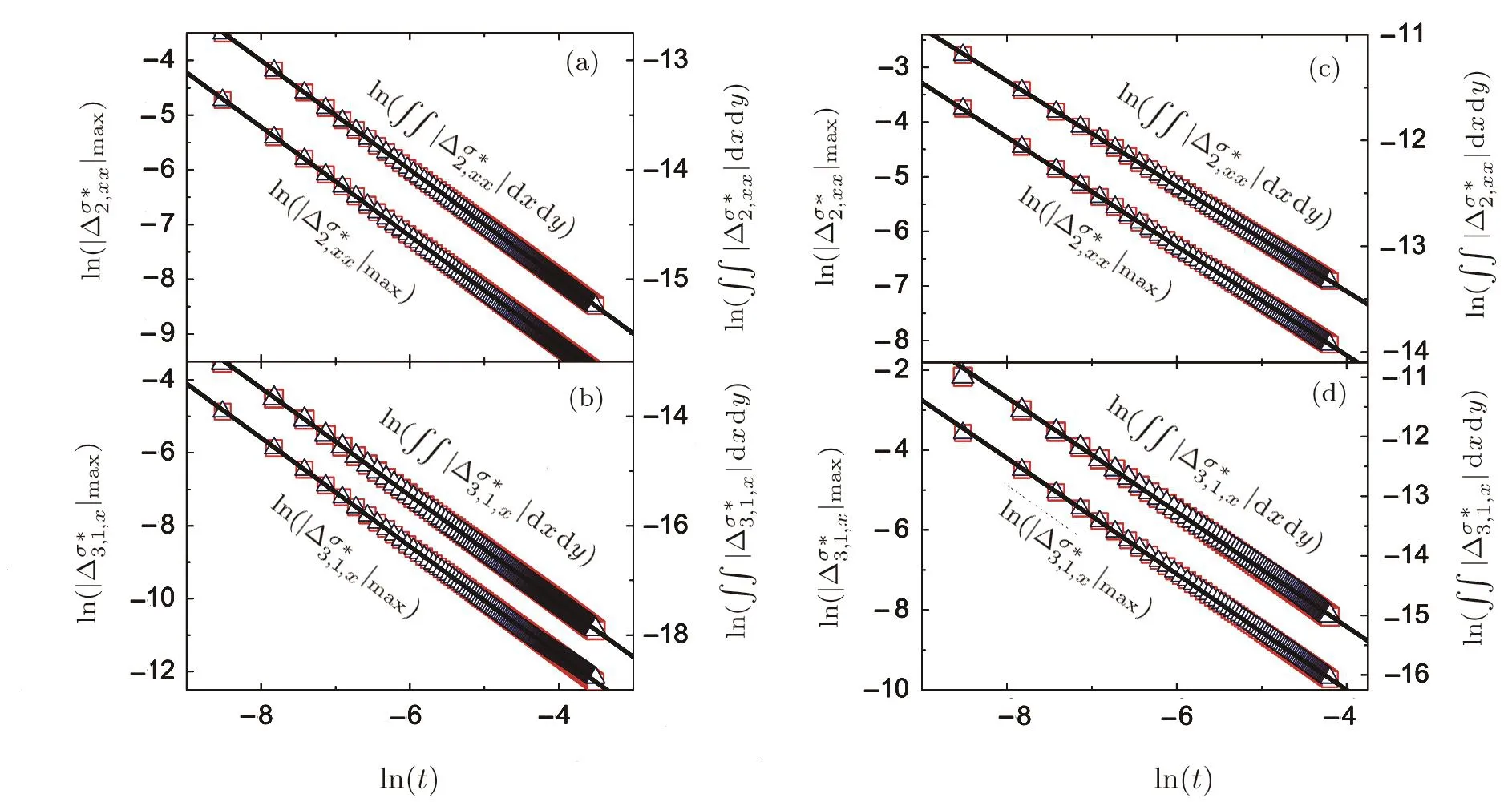
Fig.3 Evolution of nonequilibrium effects:(a)the amplitude and integral of∆σ2,xxin Case I,(b)the amplitude and integral of∆σ3,1,xin Case I,(c)the amplitude and integral of∆σ2,xxin Case II,(d)the amplitude and integral of∆σ3,1,xin Case II.

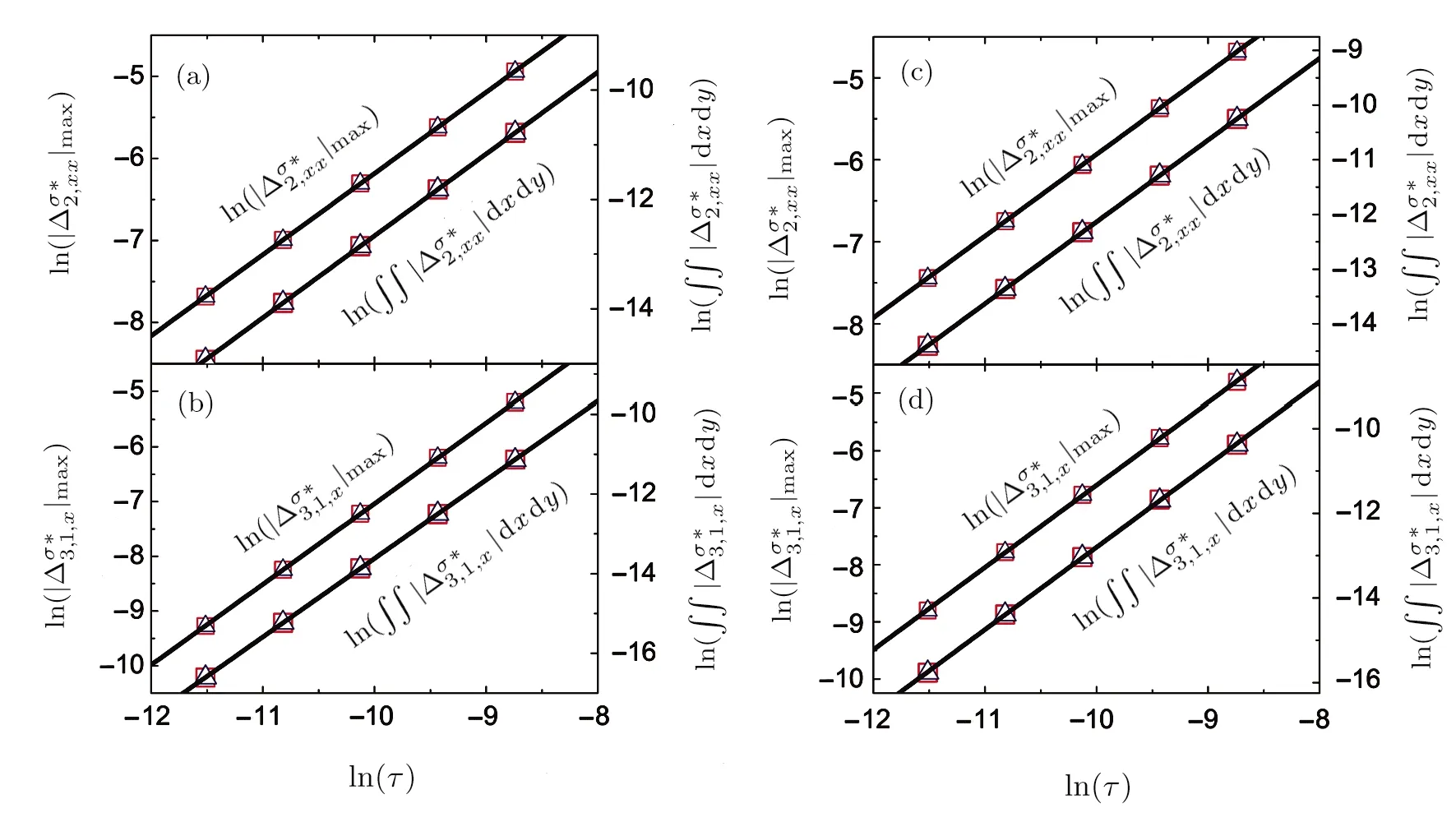
Fig.4 Nonequilibrium effects versus the relaxation time:(a)the amplitude and integral of∆σ2,xxin Group I,(b)the amplitude and integral of∆σ3,1,xin Group I,(c)the amplitude and integral of∆σ2,xxin Group II,(d)the amplitude and integral of∆σ3,1,xin Group II.

In summary,the recently developed discrete Boltzmann method is employed to investigate the TNEs in the dynamic process of binary diffusion.The departure of the velocity distribution function from its equilibrium counterpart is investigated in detail.It is found that,both the local and global TNEs around the material interface decrease with evolution due to the smoothness of physical quantities;while they are enhanced by the relaxation time.Specifically,the relations between the TNEs and the time(the relaxation time)obey a negative(positive)power law.

[1]S.R.De Groot and P.Mazur,Non-Equilibrium Thermodynamics,Dover Publications,New York(2013).

[2]S.Chapman and T.G.Cowling,The Mathematical Theory of Non-Uniform Gases:an Account of the Kinetic Theory of Viscosity,Thermal Conduction and Diffusion in Gases,Cambridge University Press,Cambridge(1970).

[3]X.Shan and G.Doolen,Phys.Rev.E 54(1996)3614.

[4]A.J.Briant and J.M.Yeomans,Phys.Rev.E 69(2004)031603.

[5]Z.Chai,C.Huang,B.Shi,and Z.Guo,Int.J.Heat Mass Transf.98(2016)687.

[6]A.S.Joshi,A.A.Peracchio,K.N.Grew,and W.K.Chiu,J.Phys.D:Appl.Phys.40(2007)7593.

[7]F.M.Liu,A.L.Wang,R.F.Qiu,and T.Jiang,Int.J.Mod.Phys.C 27(2016)1650130.

[8]J.Zudrop,K.Masilamani,S.Roller,and P.Asinari,Computers&Fluids 153(2017)20.

[9]J.G.Zhou,P.M.Haygarth,P.J.A.Withers,et al.,Phys.Rev.E 93(2016)043310.

[10]S.Succi,The Lattice Boltzmann Equation for Fluid Dynamics and Beyond,Oxford University Press,New York(2001).

[11]R.Qin and Y.Zhang,Comput.Fluids 35(2006)929.

[12]C.Zhuo and C.Zhong,Int.J.Heat Fluid Flow 42(2013)10.

[13]Y.Gan,A.Xu,G.Zhang,and Y.Li,Commun.Theor.Phys.57(2012)681.

[14]Y.Gan,A.Xu,G.Zhang,and S.Succi,Soft Matter 11(2015)5336.