直齿行星齿轮动力学建模与分析研究*

潘博 孙京 于登云 胡华君,3

(1.北京空间飞行器总体设计部,北京 100094) (2.中国航天科技集团公司,北京 100048) (3. 北京卫星制造厂, 北京 100094)

引言

行星齿轮由于具有体积小、重量轻、传动比大、效率高等特点,在空间机构,尤其是星球车车轮[1]、空间机械臂[2]中得到了广泛的应用.全面、系统地对行星齿轮的动力学特性进行分析,是研究这些空间机构的基础.

行星齿轮的动力学研究中,大多数问题都可以参照齿轮系的动力学分析方法进行分析,如啮合刚度、啮合阻尼、齿侧间隙的描述等.不同的是,行星齿轮传动结构复杂且存在过约束,对其进行动力学研究时必须考虑多个构件或运动副的弹性,因此,行星齿轮的建模、仿真更为困难.

根据建模方法和考虑因素的不同,可将行星传动的动力学模型划分为有限元模型和集中参数模型[3].通常有限元模型比集中参数模型的求解精度高,但运算量较大,不利于动态分析和实时仿真.集中参数模型是将行星传动的各个构件简化为集中质量,将各构件之间以及构件与壳体之间的连接简化为弹簧-阻尼器等,从而使行星齿轮传动系统等效为典型的多自由度弹簧-质量振动系统,更便于实时求解和动态分析.

动力学建模的目标是以最简单的表达形式来正确地描述系统中最重要的物理现象.集中参数模型物理概念清晰、表达简单,且适于动态分析和仿真计算.因此,本文采用集中参数模型对行星齿轮进行建模,以简化模型,忽略次要因素,分析其动力学特性.

1 行星齿轮纯扭转动力学一般模型

本文所研究的行星齿轮,针对直齿啮合,所以轴向载荷很小,可以忽略.另外,轴承支承刚度较大,由Kahraman[4]通过对行星齿轮固有模态计算结果的比较分析可知,当支承刚度与轮齿啮合刚度之比大于10时,可以忽略行星齿轮中轴承支承刚度的影响.并且由于关节中传动系统主要任务是承担扭转动力的传递,而结构载荷主要由壳体和轴承承担,传动系统只占结构系统的很小一部分.因此,这里可以只考虑行星齿轮扭转方向的动力学特性.

本文在Kahraman研究成果的基础上,在时变啮合刚度、时变啮合误差的表示方法上进行改进,采用纯扭转集中参数模型进行行星齿轮的动力学建模,如图1所示.

根据研究对象的特点,首先给出行星齿轮动力学模型的基本前提假设:(1)假设每个齿轮均为刚体,轮齿的柔性由一个具有时变刚度的弹簧模型模拟,作用于齿轮啮合线上；(2)假设行星架和每个齿轮仅沿扭转方向运动,即仅有一个转动自由度；(3)假设行星架和每个齿轮的偏心误差和圆度误差较小,可以忽略其影响；(4)行星架扭转刚度较大,忽略行星架的扭转柔性；(5)假设各齿轮支承刚度很大,忽略其柔性的影响.

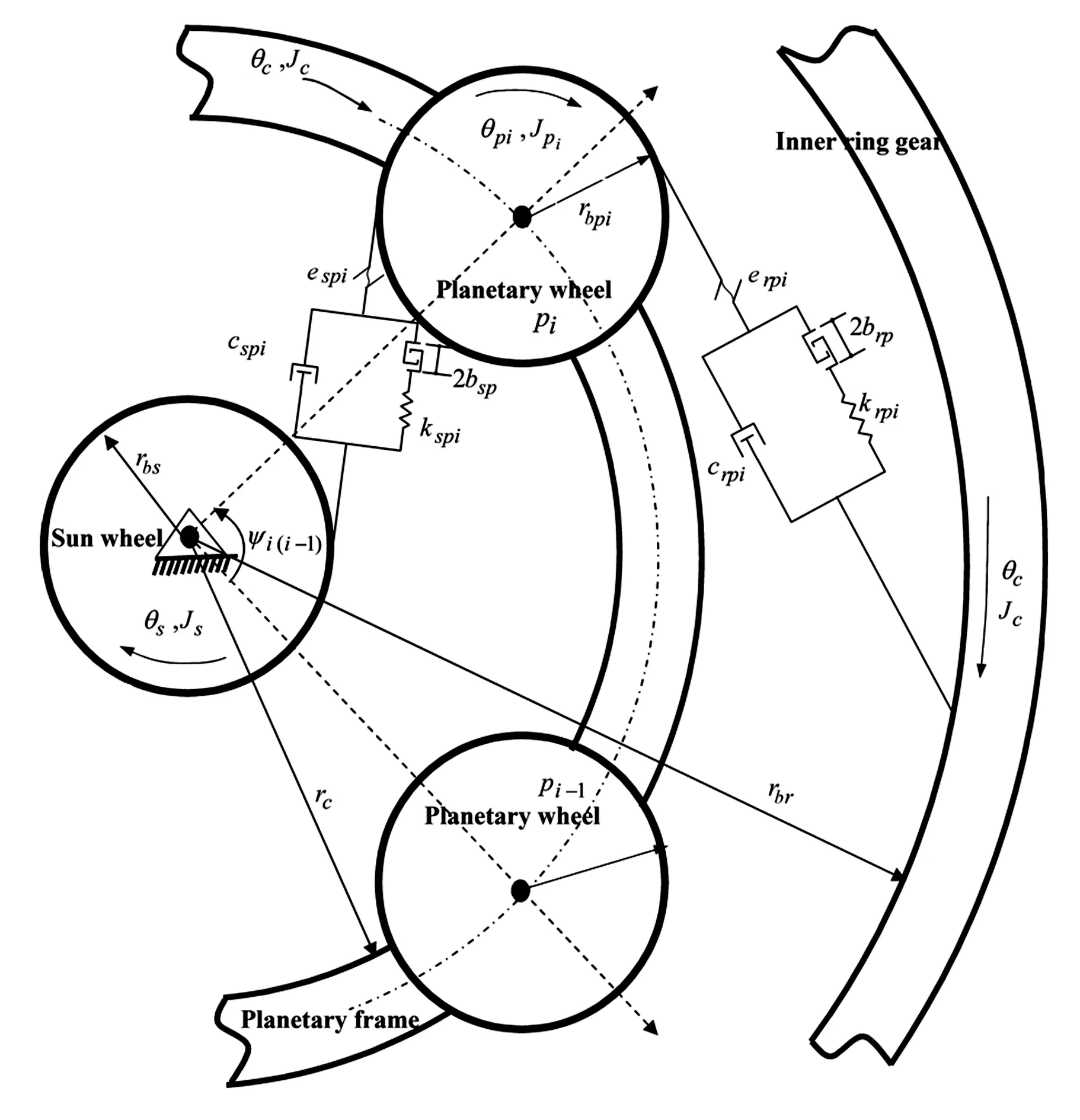
图1 行星齿轮动力学模型Fig.1 Dynamical model of planetary gear

在此基础上,可以得到行星齿轮的纯扭转动力学一般方程[5]如下,对于太阳轮s:

(1)

其中,Js为太阳轮绕其旋转轴的转动惯量；θs为太阳轮相对惯性坐标系绕其旋转轴的转角；kspi为太阳轮与第i个行星轮之间的时变啮合刚度,其具体表达见3节；cspi为太阳轮与第i个行星轮之间的啮合阻尼,其具体表达参见文献[6]；f(*,*)为间隙函数,其具体表达参见文献[7]；δspi为太阳轮与第i个行星轮之间啮合线上的相对位移；rbs为太阳轮的基圆半径；τm为驱动力矩；n为行星轮个数.

对于行星轮pi:

(i=1,2,…,n)

(2)

其中,Jp为行星轮绕其旋转轴的转动惯量；θpi为行星轮相对行星架的转角；krpi为内齿轮与第i个行星轮之间的时变啮合刚度；crpi为内齿轮与第i个行星轮之间的啮合阻尼；δrpi为内齿轮与第i个行星轮之间啮合线上的相对位移；rbp为行星轮的基圆半径.

太阳轮与第i个行星轮之间以及内齿圈与第i个行星轮之间在啮合线方向的相对位移,如式(3)和(4)所示:

δspi=rbsθs+rbpθpi-rcθccosαspi-espi

(3)

δrpi=rbpθpi-rbrθr+rcθccosαrpi-erpi

(4)

其中,rc为行星架有效半径；rbr为内齿轮的基圆半径；θc为行星架相对惯性坐标系的转角；αspi和αrpi分别为太阳轮与第i个行星轮之间和内齿轮与第i个行星轮之间的啮合角；espi和erpi分别为太阳轮与第i个行星轮之间以及内齿圈与第i个行星轮之间的啮合误差,其具体表达见4节.

在不考虑齿轮变位的情况下,齿轮的分度圆压力角和啮合角相同,按国标中对直齿轮啮合的规定:

αs=αpi=αspi=20°

(5)

其中αs和αpi分别为太阳轮和第i个行星轮的分度圆压力角.

由rc=rs+rpi,得:

rccosαspi=rscosαpi+rpicosαspi

=rbs+rbpi

(6)

因此,δspi和δrpi可简化为:

δspi=rbs(θs-θc)+rbpi(θpi-θc)-espi

(7)

δrpi=rbpi(θpi-θc)+rbr(θc-θr)-erpi

(8)

δrpi=rbpi(θpi-θc)+rbrθc-erpi

(9)

对行星架c,有:

(10)

同理,可化简为:

(rbr-rbpi)=-τL

(11)

其中,Jc为行星架绕其旋转轴的转动惯量；mpi为行星轮质量；τL为负载力矩.

将式(1～11)所示动力学方程进行组合,可得动力学方程组的标准形式:

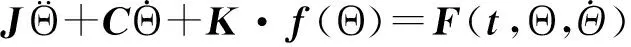
(12)

其中,Θ=[θs,θp1,θp2,θp3,θc]T,J为常值对角惯量矩阵,C和K为常值阻尼矩阵和时变刚度矩阵,f为间隙函数向量,F包括电机驱动力矩、负载力矩以及由传动误差构成的伪激励力矩.

2 时变啮合刚度的求解

对于啮合刚度的计算有多种方法,主要包括经典材料力学和弹性力学方法、有限元法[8]、经验公式法[9,10]和试验测试法[11]等.本节主要采用ISO标准提供的经验公式对啮合刚度进行估算.Vladimír Moravec和Tomáš Havlík[12]分别利用ISO标准提供的经验公式和有限元方法对齿轮的啮合刚度进行计算,发现二者的结果相差不超过15%,可见ISO标准提供的经验公式,在一定程度上可以反映齿轮真实的刚度值.

此外,直齿轮啮合刚度存在时变性,其原因[13]有两个:一是单对轮齿在作用线不同的啮合位置的啮合刚度变化；二是参加啮合的齿对数的变化.因此,对于直齿行星齿轮的建模,要正确描述这种啮合刚度的时变性.Al-shyyab A等[14]、Hbaieb R等[15]和王世宇等[3]根据直齿轮啮合刚度的这一特点,忽略单对轮齿啮合刚度的变化,假设其符合矩形波的变化规律.他们将时变啮合刚度看作时间的函数,并假设矩形波的周期恒定.这种描述方法,在分析行星齿轮稳态运动的固有特性时是有效的.但在启动或制动阶段,啮合周期是变化的,时变啮合刚度的恒定周期函数形式将不能表征真实的运动情况.对于空间机构,出于稳定性的考虑,要限制关节电机的带宽,通常机械臂关节存在较长时间的加减速过程；对于工业机器人,提高工作效率使得机械臂运转速度加快,需要频繁变化臂杆姿态,这也导致机械臂的加减速过程更为突出.而将时变啮合刚度视为时间的定周期函数,显然无法体现加减速过程中的啮合刚度变化情况.此外,矩形波的形式忽略单对轮齿啮合刚度的变化,因此与真实的啮合刚度曲线的变化形式也存在差异.本文采用时变啮合刚度的表达形式.首先,参照张建云[16]的方法,用二次曲线拟合单对齿的啮合刚度,并经过叠加求得直齿轮啮合刚度的数学表达式,这样表达比矩形波更为精确.然后,将啮合刚度假设为行星轮转角的周期函数,即啮合位置的函数(见图2).此时,啮合周期为行星轮齿数的倒数,即在任何转速下均为常数.因此,有效地解决了上述表示形式在加减速过程中啮合刚度的描述问题.最后,利用Fourier级数将表达式展开,如图3所示,从而简化了计算,易于工程应用.

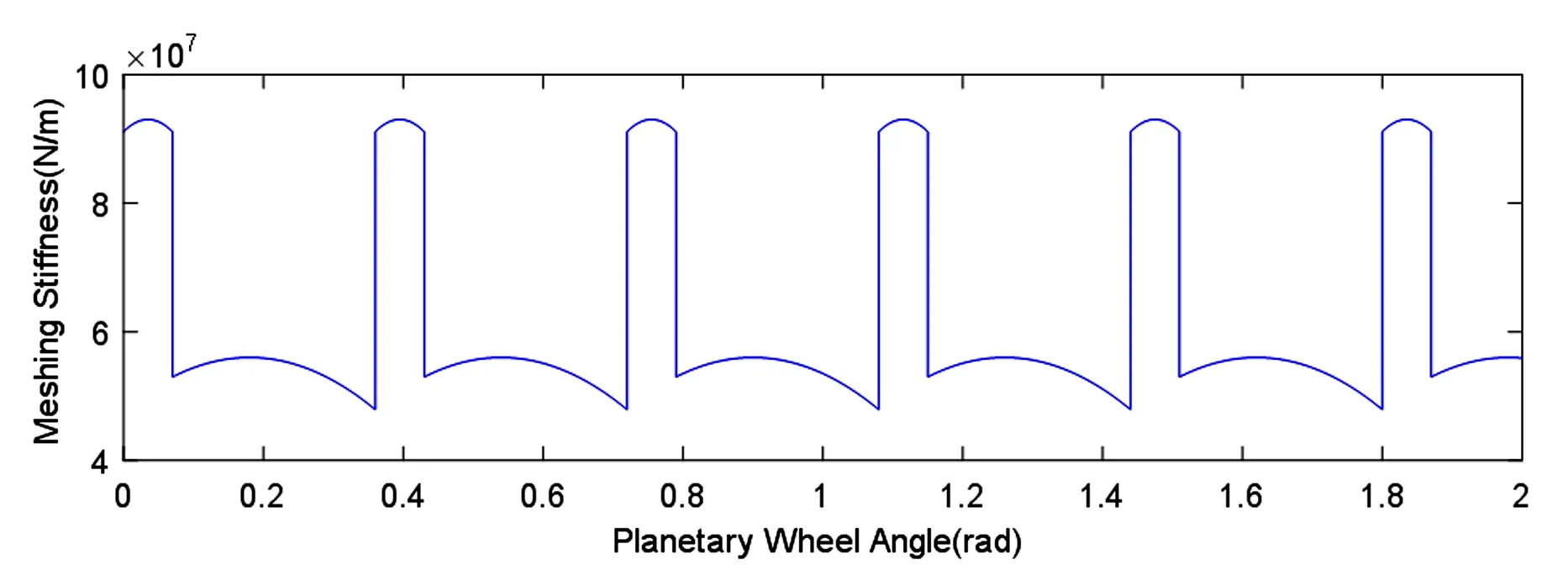
图2 以行星轮转角表示的时变啮合刚度曲线Fig.2 Time-varying meshing stiffness curve expressed in terms of planet rotation angle

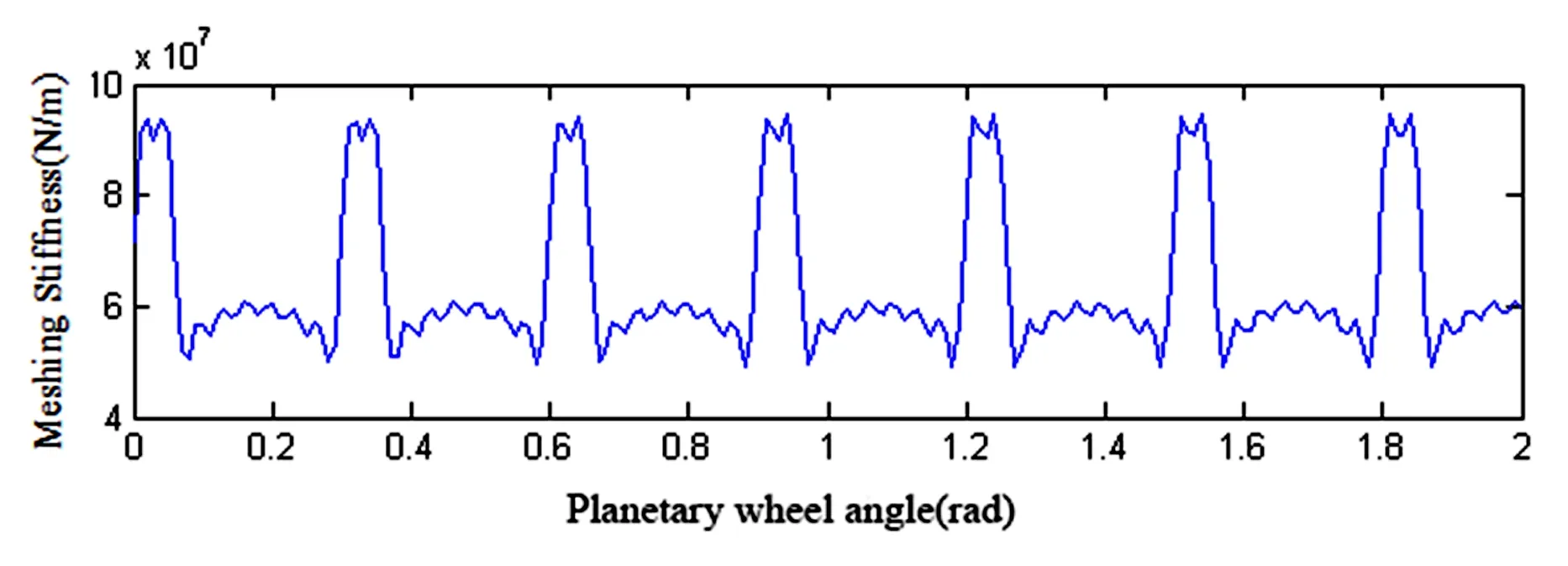
图3 新的时变啮合刚度模型的Fourier展开形式Fig.3 Fourier expansion of a new time-varying meshing stiffness model

具体作法是将时变啮合刚度表示为均值与波动值相加的形式:

(13)

这里θpi为行星轮相对惯性坐标系绕其旋转轴的转角.

这时,时变啮合刚度的周期为一恒值,它只和行星轮的齿数zp有关:

(14)

其中,pbp为行星轮基圆齿距,rbp为行星轮基圆半径,mp为行星轮模数,αp为行星轮分度圆压力角.

将时变啮合刚度的波动成分进行Fourier级数展开,得:

(15)

其中:

(16)

(17)

(18)

n=1,2,3,…

式中θ0为时变啮合刚度的初始相位.

3 啮合误差的描述

对于综合啮合误差的描述来说,王世宇[3]、孙智民[6]等将啮合误差假定为频率为啮频的正弦波.Jia等[17]将啮合误差分为几何误差和节距误差两部分,并分别假设为齿轮啮合角和齿轮转角的三次谐波函数之和.这两种描述方式的本质是一致的,都是利用Fourier级数的方式对啮合误差进行拟合,只是选取的截断误差不同.

本节主要分析啮合误差对行星齿轮整体动力学特性影响的趋势.因此为简化计算,这里采用前者的描述方法.此外,与时变啮合刚度的表示方法类似,假设啮合误差是行星轮转角的正弦函数[18],则太阳轮与行星轮之间的动态啮合误差为:

espi=Espisin(zpθpi+ϑspi) (i=1,2,…,n)

(19)

内齿圈与行星轮之间的动态啮合误差为:

erpi=Erpisin(zpθpi+ϑspi+ϑsr)

(i=1,2,…,n)

(20)

其中,θpi为行星轮相对惯性坐标系绕其旋转轴的转角,zp为行星轮的齿数,n为行星轮个数.

由行星齿轮的安装原理,行星轮与太阳轮、内齿圈之间的相位关系可表示如下:

1)第i个行星轮与太阳轮啮合的初相位:

(21)

2)第i个行星轮与内齿圈啮合的初相位:

(22)

3)第i个行星轮内、外啮合之间的相位差:

(23)

其中zs和zr分别为太阳轮和内齿轮的齿数.

根据正弦函数的周期性特点,得:

(24)

和

(25)

4 计算结果与分析

通常,对动力学系统的振动特性研究,采用量纲归一化的方法即无量纲化的方法.这样可以不用去考虑具体的单位或物理意义,使得数学求解和分析更为方便；但为了从物理概念或力学意义角度分析问题,还需将计算完的结果转换回来.此外,学者们常通过引入时间尺度和位移尺度来消除刚体位移,从而方便对模型的求解以及振动特性的分析,这同样是为了数学上求解的方便,而缺少物理意义.本节采用动态传动误差来研究系统的动力学特性,不仅消除了刚体位移,从而方便模型求解和振动特性的研究,又具有明显的物理意义,方便从真实概念角度分析系统.

这里以大增益比例环节来模拟电机等动力源的恒转速动力学特性.由于负载的波动势必影响电机的动态特性,以大增益比例环节来模拟电机的动力学特性,可以实现近似的恒定转速,实际上与真实工况更为相近,因此可以认为这种假设是合适的.精细时程积分法相对吉尔法等算法,具有高效、高精度和无条件稳定等优点[19,20].为消除系统存在刚体运动导致的刚度矩阵奇异性,李伟东等[21]将动力学方程两端同时加入附加刚度项,既消除了刚度矩阵的奇异性,又不影响方程的等式关系,进一步提高了这一算法的适用范围.为提高计算效率和计算精度,利用精细时程积分法对式(12)所示的动力学模型进行求解,积分步长0.5ms,积分时间34s.行星齿轮的基本参数为:模数均为1,齿数分别为zs=zp=21、zr=63,齿宽均为5mm,密度均为7.85×103kg/m3,分度圆压力角均为20°.

4.1 输入转速的影响分析

不考虑负载和啮合误差的影响,假定行星齿轮的齿侧间隙为100μm,改变行星齿轮的输入转速分别为500rpm、1500rpm和2500rpm.则不同的输入转速下,行星齿轮的动态传动误差曲线如图4所示.从图中可以看出,低速下,行星齿轮的动态传动误差的振动幅值较小,随着转速的增加,幅值明显增大,且其均值偏差也明显增大.这主要是由于齿侧间隙的存在,高转速下轮齿之间的冲击载荷更大所致.通过对时域曲线的频谱分析可知,行星齿轮动态传动误差的主要频率为行星齿轮的啮合频率,其与转速成线性关系,如图5所示.

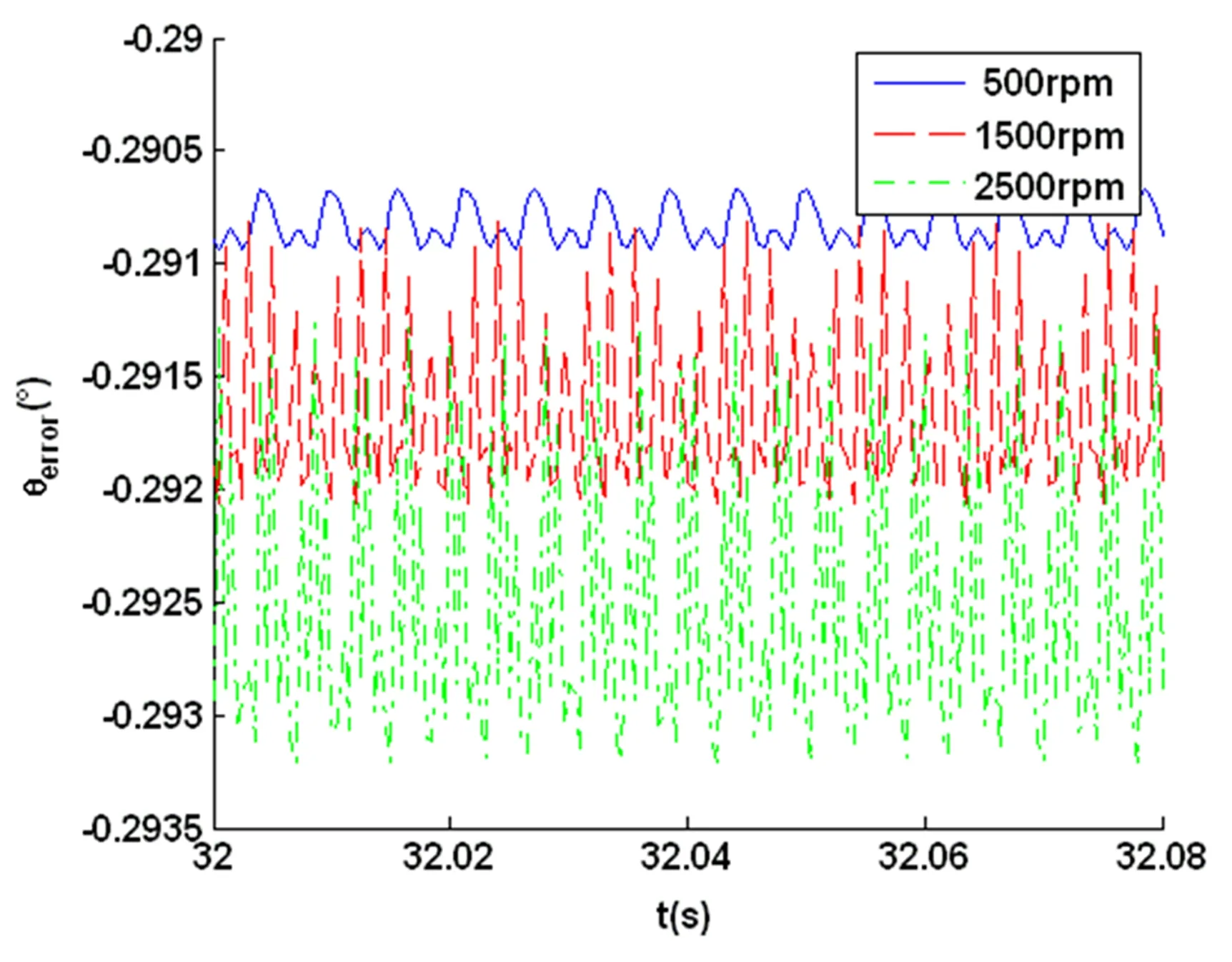
图4 不同输入转速下动态传动误差时程曲线Fig.4 Dynamic transmission error time history curve under different input speed

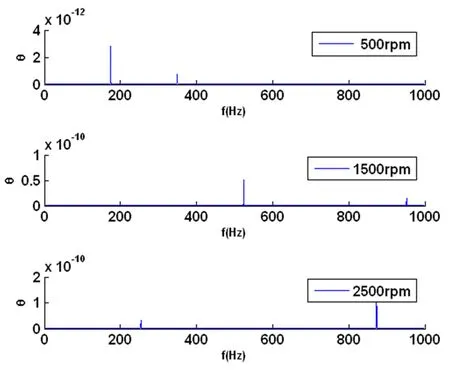
图5 不同输入转速下动态传动误差频谱特性Fig.5 The spectrum of dynamic transmission errors under different input speeds

4.2 齿侧间隙的影响分析

在其它基本参数不变的情况下,改变行星齿轮的齿侧间隙分别为0、10μm和100μm.存在间隙时,动态传动误差曲线表现为近似的简谐振动,其振动频率为行星齿轮的啮合频率,如图6和图7所示.随着齿侧间隙增大,动态传动误差的振动幅值显著增大,且大间隙下,传动误差主要呈现为负值,如图6所示.在无间隙的条件下,系统的振动幅值虽小,但频率特性中的高阶分量明显,主要呈现出前三倍啮合频率的非简谐周期振动,如图7所示.

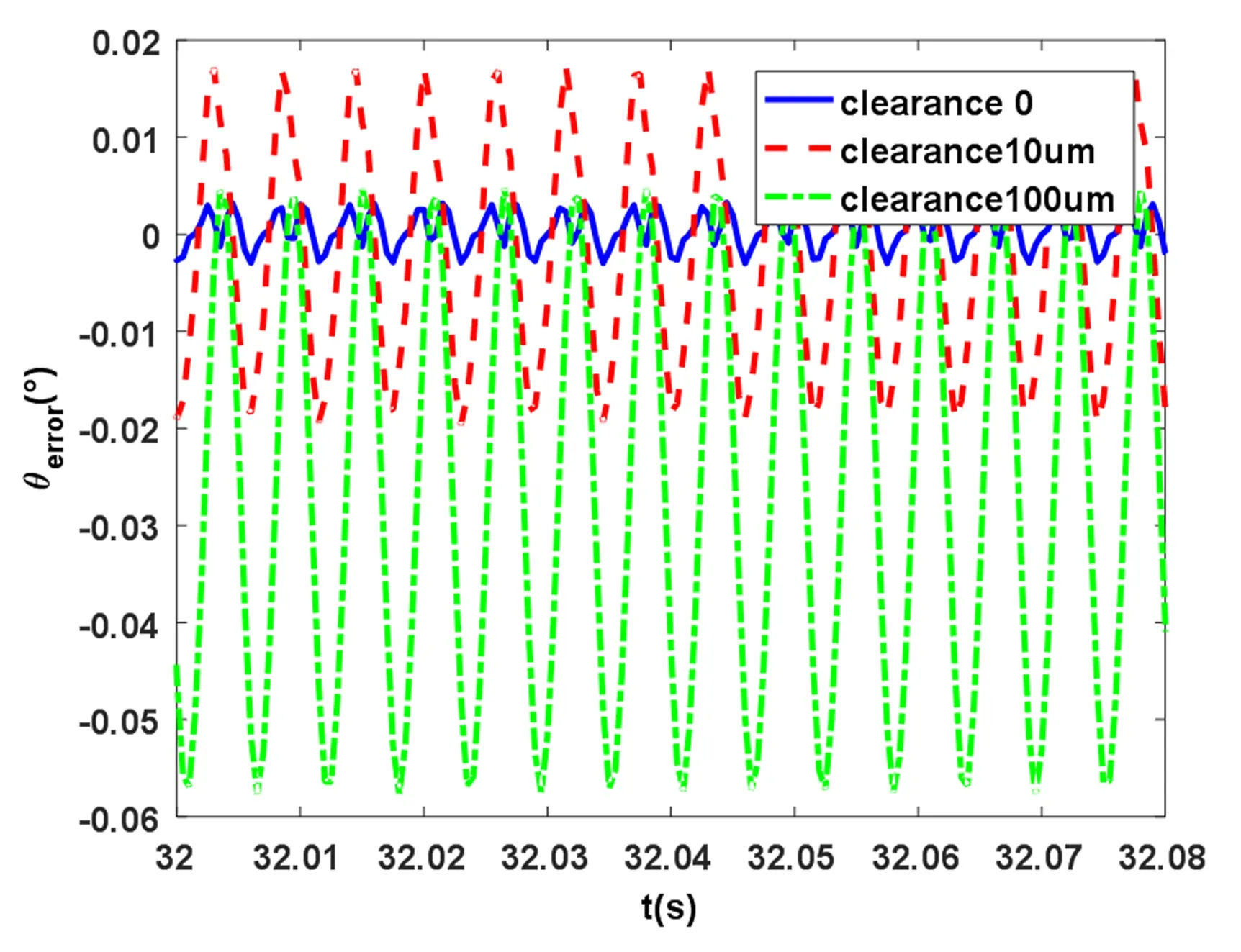
图6 不同齿侧间隙下动态传动误差时程曲线Fig.6 Dynamic transmission error time history cure under different tooth side clearance

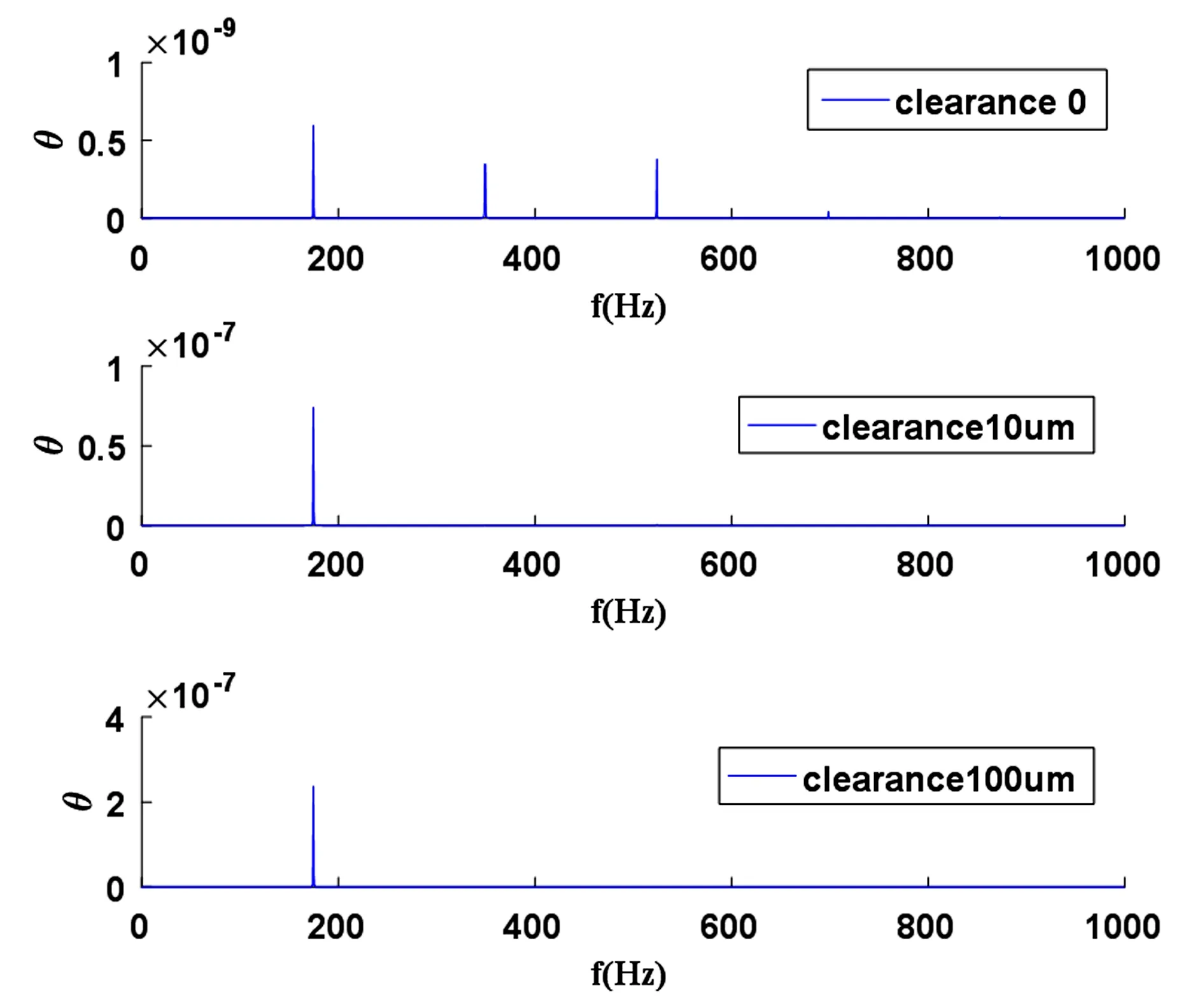
图7 不同齿侧间隙下动态传动误差频谱特性Fig.7 The spectrum of transmission errors under different tooth side clearance

4.3 啮合误差的影响分析

在其它基本参数不变的情况下,改变行星齿轮的轮齿啮合误差分别为10μm、20μm和50μm.则在不同啮合误差下,行星齿轮的动态特性及分析如图8和图9所示.改变行星齿轮的啮合误差不会影响动态传动误差的振动形式,即仍保持近似的简谐振动.但增大啮合误差的幅值会大幅增加动态传动误差的幅值.可见,提高齿轮的精度有助于改善行星齿轮整体的动态特性.

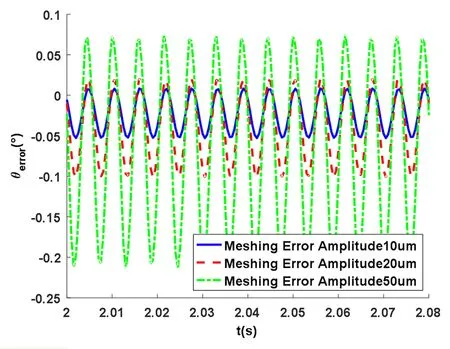
图8 不同啮合误差下动态传动误差时程曲线Fig.8 Dynamic transmission error time history curve under different mesh errors

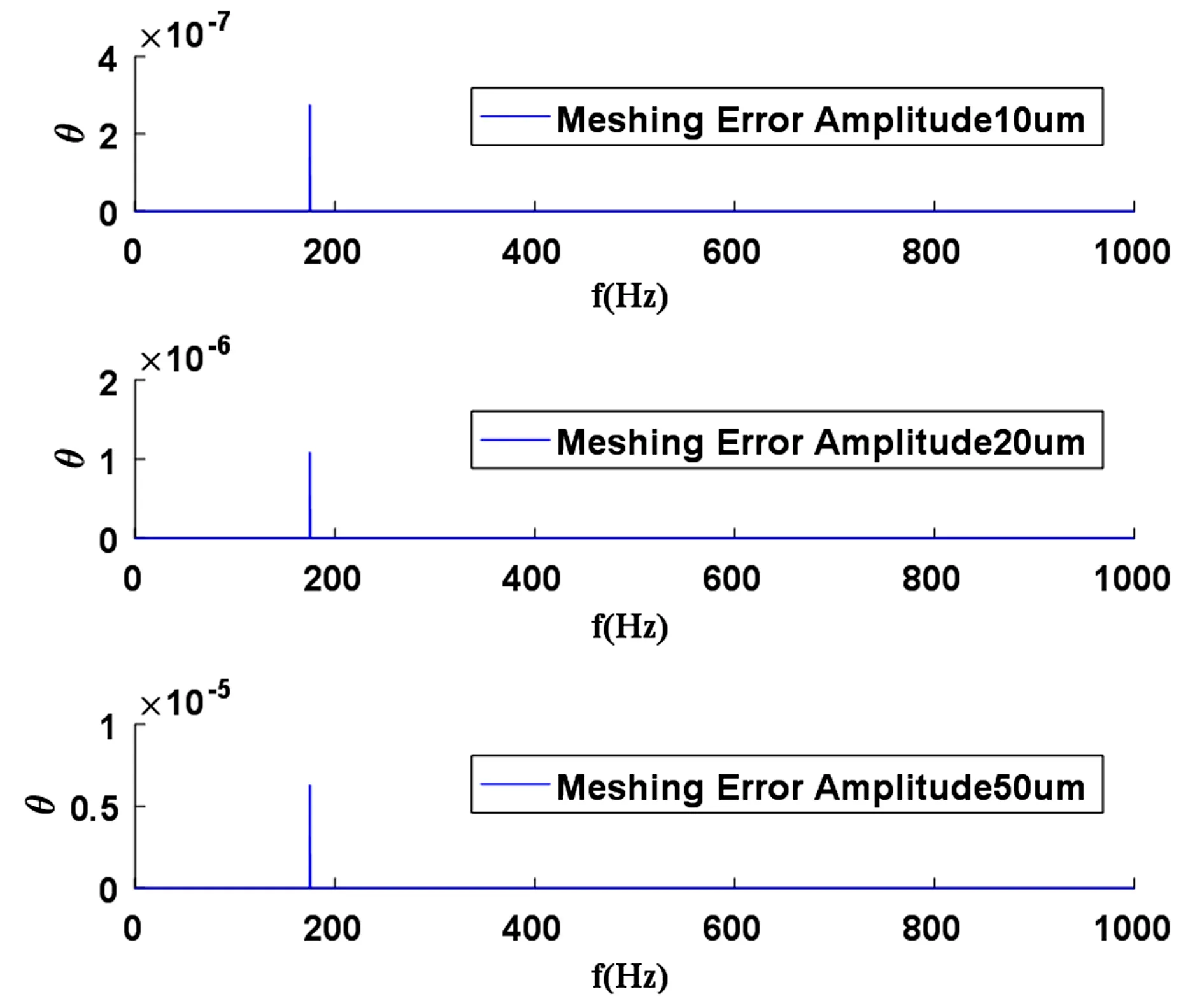
图9 不同啮合误差下动态传动误差频谱特性Fig.9 The spectrum of dynamic transmission error under different mesh errors

4.4 力矩负载的影响分析

在其它基本参数不变的情况下,改变行星齿轮的力矩负载分别为0、25N·m和50N·m.随着力矩负载的增大,动态传动误差幅值减小,且增大到一定程度时,完全为负值误差,如图10和图11所示,从受力分析角度很容易理解这种现象.但随着负载的增大,振动分量中的高频成分逐步呈现,且在大负载下,振动频率中的高频成分明显增多,振动曲线也呈现出行星齿轮啮合频率及其倍频的非简谐的周期振动.对比零间隙下行星齿轮的频谱特性,如图7,可以发现二者是相似的.可见,力矩负载的增大使轮齿的弹性变形增大,大载荷下,轮齿的间隙甚至被“吃掉”,因此,表现出零间隙下的动力学特征.

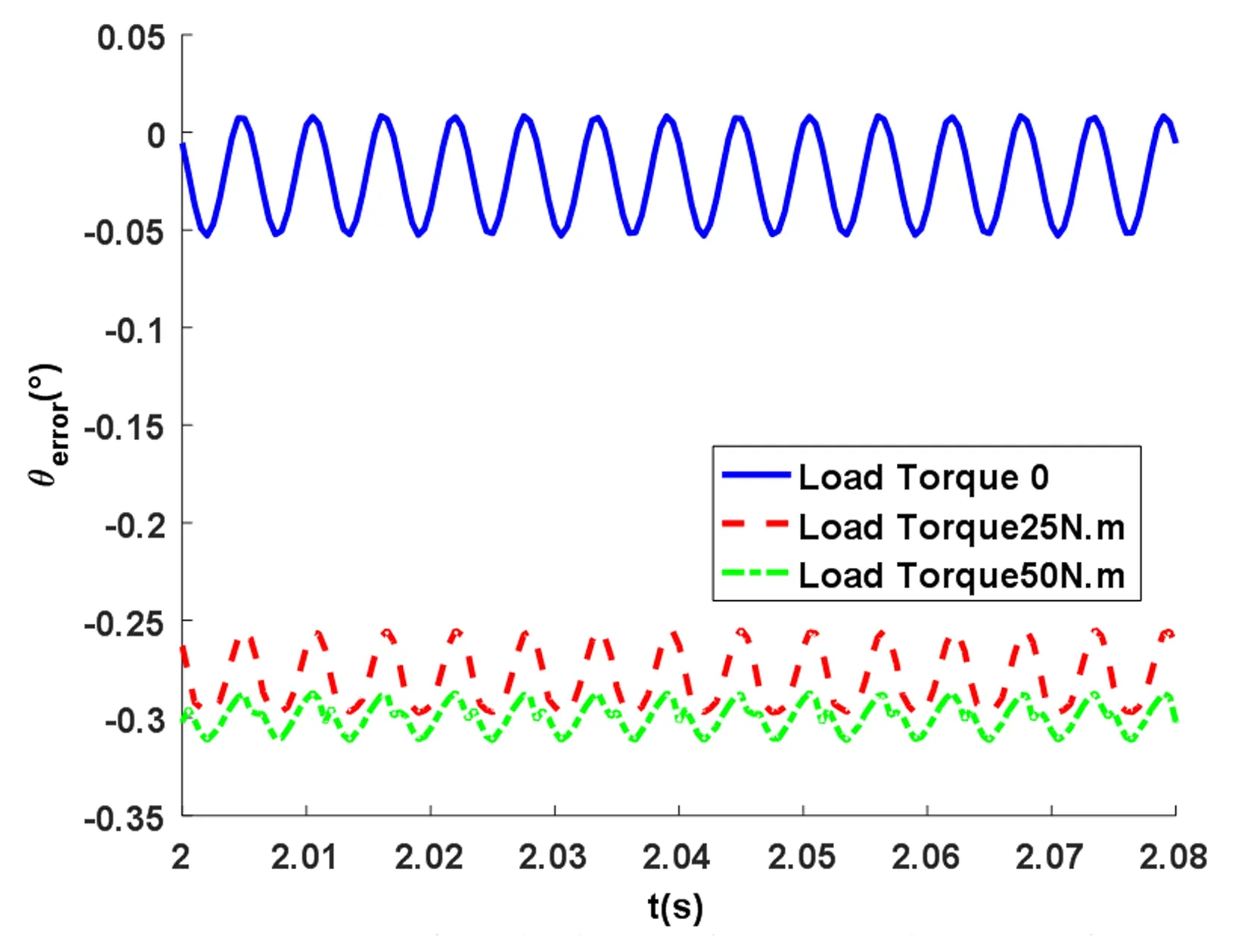
图10 不同力矩负载下动态传动误差时程曲线Fig.10 Dynamic transmission error time history curve under different torque load

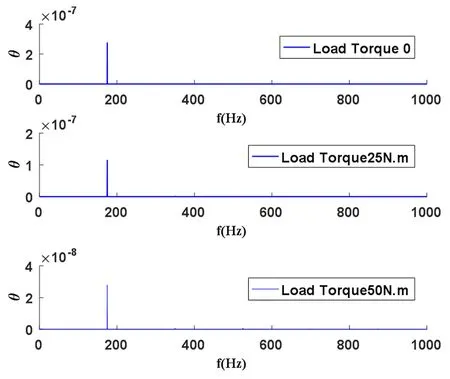
图11 不同力矩负载下动态传动误差频谱特性Fig.11 The spectrum of dynamic transmission error under different torque load

5 小结

综合考虑了时变啮合刚度、齿侧间隙和啮合误差等非线性因素,利用集中参数模型建立了直齿行星齿轮的动力学模型.提出了将时变啮合刚度、时变啮合误差表示为行星轮转角的函数,实现了时变啮合刚度、时变啮合误差在转速变化的情况下仍能进行傅里叶级数展开,从而有效解决变转速下动力学模型的描述和求解问题.并通过数值求解,得到了转速、齿侧间隙、啮合误差以及负载等重要参数对行星齿轮动力学特性的影响规律.

1Florian K, Cody H, Taj M, et al. 2011 Oregon state mars rover design report. Oregon State University Robotics Club, Oregon State University, Corvallis, Oregon, USA

2于登云,潘博,孙京. 空间机械臂关节动力学建模与分析的研究进展. 航天器工程, 2010,19(2):1～10 (Yu D Y, Pan B, Sun J. A literature review on dynamic modeling and analysis of the joints in space manipulator.SpaceEngineering, 2010,19(2):1～10 (in Chinese))

3王世宇. 基于相位调谐的直齿行星齿轮传动动力学理论与试验研究[博士学位论文]. 天津:天津大学, 2005(Wang S Y. Theoretical and experimental investigation on dynamics of spur planetary gear transmissions based on planet phasing theory[Ph.D Thesis]. Tianjin:Tianjin University, 2005 (in Chinese))

4Kahraman A. Natural modes of planetary gear trains.JournalofSoundandVibration, 1994,173(1):125～130

5Al-shyyab A. A non-linear dynamic model for planetary gear sets.JournalofMulti-bodyDynamics, 2007,221(4):567～576

6孙智民,季林红,沈允文. 2K-H行星齿轮传动非线性动力学. 清华大学学报(自然科学版), 2003,43(5) (Sun Z M, Ji L H, Shen Y W. Nonlinear dynamics of 2K-H planetary gear train.JournalofTsinghuaUniversity(ScienceandTechnology), 2003,43(5) (in Chinese))

7潘博,于登云,孙京. 大型空间机械臂关节动力学建模与分析研究. 宇航学报, 2010,31(11) (Pan B, Yu D Y, Sun J. Research on dynamic modeling and analysis of joint in large space manipulator.JournalofAstronautics, 2010,31(11) (in Chinese))

8李润方,王建军. 齿轮系统动力学——振动、冲击、噪声. 北京:科学出版社, 1997 (Li R F, Wang J J. Gear system dynamics-vibration, shock, noise. Beijing: Science Press, 1997 (in Chinese))

9Lin H H, Huston R L. On dynamic loads in parallel shaft transmissions I-Modeling and analysis. NASA Technical Memorandum 100180, AVSCOM Technical Memorandum 87-C-2, December 1987

10 GB/T 3480-1997. 渐开线圆柱齿轮承载能力计算方法. 北京:中国标准出版社, 1985 (GB/T 3480-1997. Calculation method of carrying capacity of involute cylindrical gear. Beijing:China Standards Press, 1985 (in Chinese))

11 杨晓宇. 齿轮传动系统动力学特性的有限元分析及试验方法研究[博士学位论文]. 长春:中国科学院长春光学精密机械与物理研究所, 2004,12 (Yang X Y. Finite element analysis and experiment research on dynamic characteristics of gear system[Ph.D Thesis]. Changchun:Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2004,12 (in Chinese))

12 Vladimír M. Tomáš H. Notes to design of the cylindrical gears with High Contact Ratio (HCR).JournalofMiddleEuropeanConstructionandDesignofCars, 2006,4(1):1～5

13 Virgil A, Dumitru L. The effect of cycling varying mesh stiffness on dynamic motion characteristics of spur gears. In:Annals of the Oradea University, Fascicle of Management and Technological Engineering,Volume VI (XVI), 2007

14 Al-shyyab A, Kahraman A. A non-linear dynamic model for planetary gear sets.ProceedingsoftheInstitutionofMechanicalEngineers,PartH-JournalofEngineeringinMedicine, 2007,221(4):567～576

15 Hbaieb R, Chaari F, Fakhfakh T, et al. Dynamic stability of a planetary gear train under the influence of variable meshing stiffnesses.ProceedingsoftheInstitutionofMechanicalEngineers, 2006(220):1711～1725

16 张建云,丘大谋. 一种求解直齿圆柱齿轮啮合刚度的方法. 西安建筑科技大学学报, 1996,28(2):134～137 (Zhang J Y, Qiu D M. Method for calculating spur gear mesh stiffness.JournalofXi′anUniversityofArchitecture&Technology, 1996,28(2):134～137 (in Chinese))

17 Jia S X, Howard I, Wang J D. The dynamic modeling of multiple pairs of spur gears in mesh, including friction and geometrical errors.InternationalJournalofRotatingMachinery, 2003,9(6):437～442

18 张策. 机械动力学. 北京:高等教育出版社, 2008, 1 (Zhang C. Mechanical dynamics. Beijing:Higher Education Press, 2008,1 (in Chinese))

19 孔向东,钟万勰. 柔性机械臂动力学方程的精细时程积分法. 机器人, 1998,20(5):378～381 (Kong X D, Zhong W X. A precise time integration algorithm for dynamic equations of flexible manipulations.Robot, 1998,20(5):378～381 (in Chinese))

20 裘春航,吕和祥,蔡志勤. 在哈密顿体系下分析非线性动力学问题. 计算力学学报, 2000,17(2):127～132 (Qiu C H, Lv H X, Cai Z Q. Solving the problems of nonlinear dynamics based on hamiltonian system.ChineseJournalofComputationMechanics, 2000,17(2):127～132 (in Chinese))

21 李伟东,吕和祥,裘春航等. 非线性多自由度转子系统精细数值积分. 振动工程学报, 2004,17(4):427～432 (Li W D, Lv H X, Qiu C H, et al. Precise numerical integration of nonlinear rotor system with multi-degree of freedom.JournalofVibrationEngineering, 2004,17(4):427～432 (in Chinese))