面向认知冲突的弗协调置信逻辑*
郝旭东
华东师范大学哲学系
xdhao@philo.ecnu.edu.cn
1 引言
如果将欧几里德几何的第五公设“平行公理”取消,代之以与其相冲突的命题,就会得到非欧几何,如罗巴切夫几何、黎曼几何。类似地,如果在一个逻辑理论中矛盾律与排中律都成立,那么就称之为亚氏(Aristotelian)逻辑;否则,若矛盾律或排中律在其中不成立,就称之为非亚氏(non-Aristotelian)逻辑。如果所有陈述在一个理论中都为真,则称其为不足道理论;否则,就称之为足道理论。如果一个理论是不协调的(一般意义的矛盾律在其中失效,即一个命题及其否定在其中可以都真),并且还是足道的,就称该理论是弗协调理论;并将其底层逻辑称为弗协调逻辑(paraconsistent logic,又译“次协调逻辑”“亚相容逻辑”等)。在弗协调逻辑中,一个命题及其否定不能推出任意命题。后文给出的逻辑系统C1D1本文将该逻辑系统称作C1D,其中C1的含义是指其弗协调措施来自于达·科斯塔(N.C.A.da Costa)的正加型弗协调逻辑,D是英文单词“doxic”的首字母。就是一种具有弗协调逻辑特性的多主体置信逻辑。
弗协调逻辑的先驱是波兰的逻辑学家卢卡西维茨(J.Łukasiewicz)和俄国逻辑学家瓦西里耶夫(N.I.Vasiliev)。卢卡西维茨是第一个构想形式化的弗协调逻辑的学者。1910年,他论证了亚里士多德的三段论原则是独立于矛盾律的([6],第503页),并建议构建一种“非亚氏逻辑”。1912年,瓦西里耶夫设想了一种“想象逻辑(Imaginary logic)”,在这种非亚氏逻辑中,矛盾律不再一般有效([12],第127-163页)。尽管卢卡西维茨和瓦西里耶夫没有做弗协调逻辑的具体构建工作,但他们的研究为弗协调逻辑奠定了重要的思想基础。1948年,雅思科瓦斯基(S.Jaśkowski)在他的老师卢卡西维茨的影响下,构建了第一个弗协调逻辑的形式系统([5],第143-157页):商讨逻辑(Discussive logic)。雅思科瓦斯基的基本思想是把“真”解释为“根据某人(在商讨中)的立场真”。这类似于模态逻辑“在某可能世界中为真”的描述,只不过这个可能世界,是以该商讨人为立场出发点的世界([11],第3-16页)。这样,一个公式及其否定都真,就不会导致任意公式为真的后果。
20世纪50年代,巴西逻辑学家达·科斯塔及其合作者独立于雅思科瓦斯基开始了矛盾系统(Contradictory system)的研究,并且发展出了一些具有弗协调性质(paraconsistency)的系统,比如命题演算Cn(1≤n≤ω)和谓词演算ω)和,这是如今被研究和讨论最为广泛的弗协调逻辑系统([4],第790-911页)。此外,达·科斯塔等学者还对雅思科瓦斯基的商讨逻辑进行了扩充研究,得到了一阶谓词和高阶谓词商讨逻辑系统。([3],第37-56页)这些研究工作使得雅思科瓦斯基的商讨逻辑更加完整和系统。50年代末,安德森(A.R.Anderson)和贝尔纳普(N.Belnap)为处理实质蕴涵怪论而给出了相干逻辑。相干逻辑的一个显著特征就是要求前提和结论必须要具有一个相同的命题或谓词参数。正是因为这个原则,相干逻辑就具有了弗协调逻辑的性质。弗协调相干逻辑主要是由澳大利亚的逻辑学者卢特雷(R.Routley)([7],第51-68页)、梅耶尔(R.K.Meyer)([8],第183-194页)、普利斯特(G.Priest)([9],第219-241页)等人研究并发展的。此外,阿鲁达(A.I.Aruda)和达∙科斯塔还给出了弗协调相干逻辑系统P和P*。([1],第33-49页)总体来说,弗协调逻辑有三种类型:相干型,即上文所述的弗协调相干逻辑类型;弃合型,以雅思科瓦斯基所创立的商讨逻辑为代表;正加型,即给正命题逻辑系统增加适当的否定词,即着力于对经典否定词的修正,这是达·科斯塔开创的弗协调逻辑的主流方向,迄今更多地表现于与相干方向的结合,如普利斯特著名的LP(悖论逻辑)系统。
总之,弗协调逻辑是如今被广泛而深入研究的重要逻辑分支。(更多的细节内容可参阅[4,10,11])由于正加型弗协调逻辑尽量保留了经典逻辑的很多与矛盾律无关的重要推理模式,所以本文的研究和讨论范围仅限于正加型弗协调逻辑。正是通过对正加型弗协调逻辑的长期考察与探究,我国学者张建军提出了可以为弗协调逻辑“找到一种可以刻画人类信念系统之‘容错’性的‘置信语义’”([15],第614页)的观点。基于对这一观点的认同,本文以此为指针尝试性地给出了弗协调多主体置信逻辑系统C1D的语法和语义,并证明了其可靠性和完全性。以其特征内定理为切入点,通过透彻解析C1D容忍矛盾冲突的逻辑机制,详尽阐释其作为一种解悖方案的合理性与必要性,清晰展示其容忍信念冲突的特殊处理方式。
2 C1D的形式语言
将C1D的形式语言记作L0,它包括如下初始符号:
(1) 命题符p,q,r,s,···;
(2) 联结词¬,∧,∨,→;
(3) 信念算子Biα(i∈N);
(4)左右括号。其中,Bmp表示认知主体m相信p。
公式的定义如下:
(1)任意的命题符是公式;
(2)如果α和β是公式,那么(α∧β)、(α∨β)、(α→β)、¬α以及Biα(i∈N)是公式;
(3)只有按照步骤(1)和(2)得到的符号序列才是公式。
令Form(L0)表示所有公式的集合,用大写希腊字母表示任意的公式集,小写希腊字母表示任意的公式。另引入一些缩写和语法符号:
(1)α↔β表示(α→β)∧(β→α);
(2)αo表示¬(α∧¬α)。αo的直观含义是α遵守矛盾律,即α是举措得当的(well-behaved);而若α∧¬α成立,则称α是举措失当的(bad-behaved)([4],第799-800页);
(3)∼α表示(¬α∧αo)。(¬α∧αo)直观含义是遵守矛盾律的否定,即经典否定;
(4)语法符号“⊢”仍表示形式可推演关系。
3 C1D的公理系统
下列(1)-(12)都是弗协调命题演算C1的公理模式([4],第800页),(13)和
(14)则是关于认知算子的公理模式。
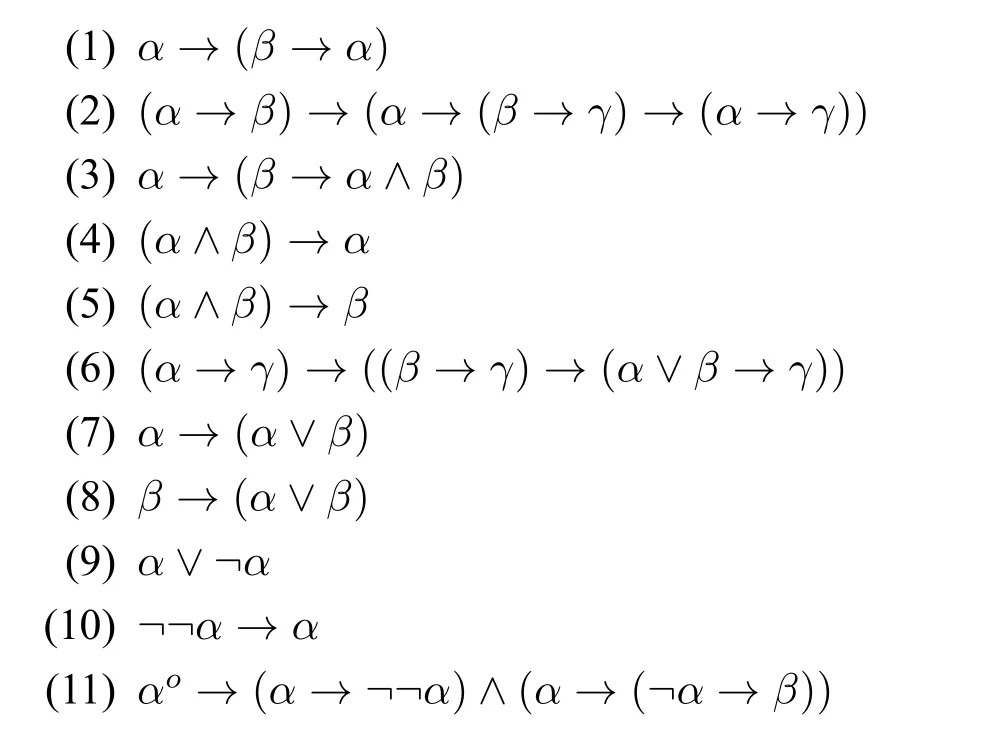

C1D的推理规则有两条:
R1: 由⊢α和⊢α→β,可以推出⊢β。
R2: 由⊢α,可以推出⊢Biα,(i=1,···,m,m∈N)。
4 C1D的语义
定义1框架F是一个多元组(W,R1,···,Rm);其中,W是认知世界或状态的集合;Ri是W上的一个二元关系,i=1,···,m(m∈N)。
定义2一个关于i=1,···,m(m∈N)的赋值就是一个从(L0)×W到{1,0}的映射,对于α,β∈Form(L0)而言满足以下条件(符号“⇒”的意思是“如果……,那么……”,符号“⇔”的意思是“当且仅当”):
(1)V(α,w)=0⇒V(¬α,w)=1
(2)V(¬¬α,w)=1⇒V(α,w)=1
(3)V(βo,w)=V(α→β,w)=V(α→¬β,w)=1⇒V(α,w)=0
(4)V(α→β,w)=1⇔V(α,w)=0或V(α,w)=1
(5)V(α∧β,w)=1⇔V(α,w)=1且V(β,w)=1
(6)V(α∨β,w)=1⇔V(α,w)=1或V(β,w)=1
(7)V(αo,w)=V(βo,w)=1⇒((α△β)o,w)=((▽α)o,w)=1;
其中△∈{∧,∨,→},▽∈{¬,Bi},i=1,···,m(m∈N)
(8)V(Biα,w)=1⇔对任一i(i=1,···,m,m∈N),任一w′∈W,wRiw′⇒V(α,w′)=1
定义3一个关于认知主体i(i=1,···,m,m∈N)的模型M=(W,R1,···,Rm,V),其中,(W,R1,···,Rm)是一个框架,而V该框架的一个赋值。
定义4令M=(W,R1,···,Rm,V)是任一模型,F=(W,R1,···,Rm)是任一框架,α是Form(L0)中的任一公式,w是W中的任一信念世界认知状态:
(1)若V(α,w)=1,则称α在w中真,记作M⊨αw;若V(α,w)=0,则称α
在w中假,记作M⊭αw;
(2)公式α在M中是可满足的,当且仅当,存在w∈W使得V(α,w)=1;
(3)公式α在M中是有效的,当且仅当,对于任一w∈W都有V(α,w)=1;
(4)公式α在F上是有效的,当且仅当,对于任一(W,R1,···,Rm)上的V都有V(α,w)=1。
定义5(C1-变形) 令α是Form(L0)中的任一公式,C1-变形记作α′,它其实就是对公式删除所有认知算子的结果。严格来说,C1-变形就是一个从一个公式到另一个公式的映射:

5 C1D的一些定理和推论
由于C1D包含了C1所有公理模式和推理规则所以C1D是C1的真扩张,所以C1的定理都将是C1D-定理;也将包含经典逻辑命题演算的所有正推理模式和正定理。例如,在C1D中有C1的如下的定理1-4。([4],第797-803页)
定理1⊢α→α
定理2在C1D中有:
(1)若α∈Γ,则Γ⊢α;
(2)若有Γ⊢α和Γ⊆∆,则有∆⊢α;
(3)若有∆⊢α和∆⊢α→β,则有∆⊢β;
(4)若有Γ⊢α和∆,α⊢β,t则有Γ,∆⊢β。
定理3在C1D中有:
(1)若有Γ1⊢α,Γ2⊢α→β,Γ1,Γ2⊆∆,则有∆⊢β。特别地
当Γ1=∅,若有⊢α,Γ2⊢α→β,Γ2⊆∆,则有∆⊢β;
当Γ2=∅,若有Γ1⊢α,⊢α→β,Γ1⊆∆,则有∆⊢β;
(2)若有Γ⊢α1→α2,Γ⊢α2→α3,···,Γ⊢αm-1→αm,则有Γ⊢α1→αm;
(3)Γ⊢α∧β当且仅当,Γ⊢α且Γ⊢β;
(4)若Γ⊢α,则Γ⊢α∨β且Γ⊢β∨α;
(5)若Γ,α⊢γ且Γ,β⊢γ,则有Γ,α∨β⊢γ;
(6)若Γ,α⊢β,则Γ⊢α→β(演绎定理);
(7)若Γ⊢αo,Γ⊢α→β,Γ⊢α→¬β,则Γ⊢¬α。
定理4⊢α→β⇒(⊢Biα→Biβ),i=1,···,m(m∈N)。
定理5在C1D中有:
(1)⊢αo⇒⊢(Biα)o,i=1,···,m(m∈N);
(2)⊢α⇒⊢Biα,i=1,···,m(m∈N)。
证明:
(1)由于有⊢αo,因而就存在一个有穷的公式序列α1,···,αh,使得αh=αo,并且对于任一j(l≤j≤h)使得αj满足下列条件之一:
(a)αj是C1D的一个公理;或者
(b)存在l,k<j使得αj可以从αl和αk(=αl→αj)通过规则R1得到;
(c)存在l≤j使得αj(=Biαl)可以从αi通过规则R2得到。
这样,由公理(13)αo→(Biα)o,从αm(=αo),使用R1,可得(Biα)o。
因此,公式序列α1,···,αh,(Biα)o就是⊢(Biα)o的证明。
(2)类似于(1)的证明,通过形式可推演的定义易证,略。 □
推论1任一C1D-定理的C1-变形都是C1-定理。
证明:类似于模态逻辑中P-变形的证明,施归纳于证明长度即可。该推论说明,若α是C1D-定理,则α′一定是C1-定理;若α不是C1-定理,则α′就不是C1D-定理。 □
推论2对于i=1,···,m(m∈N),下述公式不是C1D-定理:

证明:首先 (1)Bi¬(α∧¬α)不是C1D-定理。因为其C1-变形是¬(α∧¬α),而¬(α∧¬α)不是C1-定理([4],第801页),所以,根据推理1,Bi¬(α∧¬α)就不是C1D-定理。(2)-(10)的证明类似。 □
6 C1D的可靠性和完全性
定理6C1D的所有公理在任意框架上有效。
证明:首先根据定义2和4易验证公理(1)-(12)在任意框架上有效。下面验证公理(13)和(14)在任意框架上有效:
(1) 公理 (13)αo→(¬α)o∧(Biα)o(i=1,···,m,m∈N)在任意框架上有效。首先,根据定义2和4易验证公理αo→(¬α)o在任意框架上有效。其次,验证αo→(Biα)o在任意框架上有效:
- 当V(αo,w)=0,根据定义 2(3),则有V(αo→(Biα)o,w)=1;
- 当V(αo,w)=1,根据定义 2(7),则有V((Biα)o,w)=1;
这样根据定义2(3),可得V(αo→(Biα)o,w)=1。由于w是任意的,因此,根据定义4可知,αo→(Biα)o在任意框架上有效。因此,αo→(¬α)o∧(Biα)o(i=1,···,m,m∈N)在任意框架上有效。
(2)公理(14)Bi(α→β)→(Biα →Biβ)(i=1,···,m,m∈N)在任意框架上有效。
假若公理 (16)Bi(α→β)→(Biα→Biβ)(i=1,···,m,m∈N)并非在任意框架上有效,那么就有(W,R1,···,Rm)⊭Bi(α →β)→(Biα→Biβ)(i=1,···,m,m∈N),于是就存在一个模型 (W,R1,···,Rm,V)使得(W,R1,···,Rm,V) ⊭Bi(α→β)→(Biα→Biβ)(i=1,···,m,m∈N);即,存在w∈W使得V(Bi(α→β)→(Biα→Biβ),w)=0;于是就有

于是,对于任一则有

于是,对于任一则有

由于④和⑧会导致荒谬,所以假设不成立。故,公理(14)Bi(α→β)→(Biα→Biβ)(i=1,···,m,m∈N)在任意框架上有效。 □
定理7对于i=1,···,m,m∈N,令F是任一框架类,
(1)若α和α→β在F上有效,则B在F上有效;
(2)若α在F上有效,则Biα在F上有效。
证明:(1)的证明类似于模态逻辑中的证明,略。
(2)的证明:若α在F上有效,令(W,R1,···,Rm)是中的任一框架,V是该框架上的任一赋值。于是,对于任一w∈W,则有V(A,w)=1;因此可得,对于任一w′∈W,wRiw′⇒V(α,w′)=1;于是就有对于i=1,···,m,V(Biα,w)=1;由于w的任意性,所以就有 (W,R1,···,Rm)⊨Biα;由于 (W,R1,···,Rm)的任意性,因此就有对于i=1,···,m,F ⊨Biα;即,对于i=1,···,m,Biα在 F上有效。 □
定理8C1D是可靠的,即,若⊢C1Dα,则⊨C1Dα。
证明:首先,根据定理6,公理模式在C1D-框架上有效。其次,定理7表明C1D的推理规则在任一框架上有效。所以,C1D是可靠的。 □
定义6
(1)对于任一公式集,令,若,则称Γ是演绎封闭的。
(2)称Γ是不足道的,当且仅当,;否则,称之为足道的。
(3)称Γ是不协调的,当且仅当,有公式A使得Γ⊢A且Γ⊢¬A。否则,称之为协调的。显然,空集是总是协调的。
(4)称一足道集Γ是极大的,当且仅当,对任意公式α,若α/∈Γ则Γ∪{α}是不足道的。
引理1令Γ⊆Form(L0),α∈Form(L0),则有:
(1)如果有Γ⊢α∧∼α,那么有Γ是不足道的;
(2)如果Γ是不足道的,那么存在公式α使得Γ⊢α∧∼α;
(3)Γ⊢α,当且仅当,Γ∪{∼α}是不足道的;
(4)如果Γ是极大足道的且α/∈Γ,那么Γ∪{α}⊢α∧∼α;
(5)如果Γ是极大足道的且α/∈Γ,那么Γ∪{α}⊢¬α。
引理2令Γ⊆Form(L0),α,β∈Form(L0),若Γ是极大足道集,则有:
(1)Γ⊢α,当且仅当,α∈Γ;
(2)若α∈Γ,则∼α/∈Γ;若∼α∈Γ,则α/∈Γ;
(3)α∈Γ或∼α∈Γ;
(4)若⊢α,则α∈Γ;
(5)若α∈Γ,α→β∈Γ,则β∈Γ。
引理3令Γ⊆Form(L0),α,β∈Form(L0),若Γ是极大足道集,则有:
(1)若βo,(α→β),(α→¬β)∈Γ,则¬α∈Γ;
(2)α→β∈Γ,当且仅当,α/∈Γ或β∈Γ;
(3)α∧β∈Γ,当且仅当,α∈Γ且β∈Γ;
(4)α∨β∈Γ,当且仅当,α∈Γ或β∈Γ;
(5)Ifα∈Γ且(¬α)/∈Γ,z则(¬¬α)∈Γ;若α/∈Γ且(¬α)∈Γ,则(¬¬α)/∈Γ;
(6)若αo,βo∈Γ,则 (α→β)o∈Γ,(α∧β)o∈Γ,(α∨β)o∈Γ,(¬α)o∈Γ,(Biα)o∈Γ(i=1,···,m,m∈N)。
证明:引理1(1)到3(5)都是C1-定理,因而它们也都是C1D-定理。下面证明引理3(6)是C1D-定理。

同理,由公理(12)和(13),易证(6)的其余内容也成立。 □
引理4每一个足道集都可以扩张成极大足道集。
证明:与经典逻辑林顿巴姆引理的证明类似,略([16],第39-40页)。 □
引理5Γ⊢α,当且仅当,α是maxΓ中任一极大足道集的元素,即,∀X∈maxΓ(α∈X),特别地,当Γ=∅时,⊢α,当且仅当,α是任一个极大足道集的元素。
证明:首先,有

其次,有

因而,就有Γ⊢α⇔∀X∈maxΓ(α∈X)。
所以,当Γ=∅,就有⊢α⇔∀X∈maxΓ(α∈X)。 □
定义7是一个典范模型(canonical model),其中

引理6V满足定义2的(1)-(7)。
证明:首先,我们可以使用引理3(1)来验证满足定义2(4)。即验证若有,则有。
给定,则

类似地,使用引理3(2)-(6),可以验证满足定义2(2)-(7)。□
引理7是C1D-模型。
证明:根据引理6,验证满足定义2(1)-(7)。

下面我们验证满足定义2(8)。Biβ1,···,Biβp∈X为已知,根据引理 3(3),则有

由①和②,可得,即,满足定义2(8)。因此,是C1D-模型。 □
定理9 C1D是完全的,即,若⊨C1Dα,则⊢C1Dα。
证明:若已知⊨C1Dα,假设⊬C1Dα,根据引理5,就存在一个极大足道集w使得α/∈w。因为,所以就有。同时,由于是C1D-框架,所有就有。这与已知不符,所以假设不正确,因而,就有⊢C1Dα。 □
7 结论
弗协调多主体置信逻辑C1D为我们提供了处理矛盾冲突的一种简单易行的逻辑途径。那么,为什么C1D可以容忍认知领域的矛盾冲突呢?下面,我们就在给出答案的同时,也通过实例分析的方式显示C1D在实用方面的逻辑价值。
7.1 C1D可以作为相信者悖论解悖方案
相信者悖论最早是由伯奇(T.Burge)在1978年提出的([2],第21-35页),它是一种典型的认知悖论。类似于说谎者悖论,它也源自一个自指的陈述;通过逻辑的推导,就可以得到一个严格意义的悖论Biα↔¬Biα。在此,我们仅以最简单的方式对之进行可以满足我们说明C1D性质的描述(更多细节见[14],第176-180页)。类似于说谎者悖论,相信者悖论也是由一个自指性语句构成的,我们将该语句用α表示,它断言:认知主体i不相信α;用公式可将α定义为:

现在的问题是:认知主体i相信还是不相信α?在接受C1D的规则R2以及公理Biα→α的基础上,则有如下推断:
一方面,若有Biα,根据公理Biα→α,则有α;而α即为“认知主体i不相信α”,即有¬Biα。因此,就有Biα→¬Biα。另一方面,若¬Biα,由于“认知主体i不知道α”正是α,即有α;于是根据规则R2,可得Biα。所以,就有¬Biα→Biα。这就是说,如果Biα为真,那么它就为假;如果Biα为假,那么它就为真。于是,我们就得到了一个矛盾等价式Biα↔¬Biα。这就是造成了相信者悖论。
出现这种真矛盾(dialetheia或true contradiction)2“真矛盾”是普利斯特用来阐释其LP系统语义的特有术语([11],第4页)。该术语用来描述那些形如α∧¬α,但并没有在实际上导致包含它的理论变得不足道的公式。此处,我们扩展了真矛盾概念的范围。因为绝大多数严格意义的逻辑悖论的语形都是α↔¬α,既然弗协调逻辑将悖论归为真矛盾,那么真矛盾的范围就应该包括那些形如α↔¬α,但实际上并没有导致包含它的理论变得不足道的那些公式。会有怎样的后果?
我们知道,如果去掉C1D的公理模式(9)-(13),就可以得到一个基于经典逻辑的置信逻辑系统,这是一种经典认知逻辑(即,基于经典逻辑的认知逻辑)。由于公式(α↔¬α)→β是经典逻辑的定理,因而利用公理(16)和R2易证其包含信念算子的形式(Biα↔¬Biα)→Biβ也将是经典认知逻辑的定理。这即是说,经典认知逻辑不允许认知主体同时相信一个陈述及其否定;换言之,以经典认知逻辑为基础,存在相信者悖论的后果就是相信所有陈述。这就意味着相信者悖论在包含它的知识信念系统中爆炸了,从而导致了该知识信念系统的理性崩溃;而导致相信所有陈述的理论显然是毫无意义或不足道的。
但实际上,在我们的知识信念领域中,存在着很多认知悖论。很多时候我们不能因为在某理论中出现了这种悖论,就断然认为该理论在事实上全无意义、毫不足道。例如,尽管在素朴集合论中有罗素悖论,但这种集合论仍然可以很好地帮助我们解决初等数学以及日常思维领域中的相关问题。面对各种形如Biα↔¬Biα的认知悖论,为了避免相信一切的后果,我们的逻辑基础显然就不能是经典认知逻辑;就必须是一种可以容忍悖论,但同时又不会导致爆炸性后果的逻辑。C1D正是这样的逻辑;因为根据推论2,公式(Biα↔¬Biα)→Biβ将不再是该系统的定理;所以,以C1D为基础逻辑,相信者悖论就不会导致相信一切的爆炸性后果。
但同时我们也应当清楚地知道,C1D方案并没有真正解决悖论问题,它只是容忍了悖论。更准确地说,经典逻辑的思路是“解悖”,要求我们解决和消除悖论;而C1D方案是要“容悖”,为的是即使不消除悖论,也不会导致理性崩溃。其思路的合理性在于,解决和消除相信者悖论或其它认知悖论的确很重要,但直到现在,也没有哪种方案可以令各方都完全满意。在彻底解决这些悖论之前,面对这些认知悖论的事实存在,既然我们在事实上没有失去逻辑理性,那么我们就需要一种可以容忍悖论的基础逻辑。在含有悖论的前提下,弗协调认知逻辑C1D并没有像经典认知逻辑那样,进而就要求我们去相信一切;因而,这就十分有利于成为那些虽然含有某些认知悖论,但在某些方面仍有价值和意义的认知理论的基础逻辑。
7.2 C1D可以作为含有冲突信念理论的基础逻辑
如果信念领域出现了矛盾状况,我们就说出现了信念冲突。这是经典逻辑所不能容忍的,因为公式(α∧¬α)→β是经典逻辑的定理。这就意味着,如果矛盾是成立的,那么就会导致任意陈述的成立。或者说,经典逻辑认为矛盾状况就意味着不足道;如果一个理论出现了矛盾状况(冲突、不协调),那就意味着理论的不足道和无意义。这即是说,经典逻辑要求不能有矛盾;如果理论本身不排除矛盾,就会导致该理论在逻辑上变得毫无价值。所以,经典逻辑显然就不适于处理这种虽然不协调但足道的状况。面对这种状况,我们就需要那种可以将不协调与不足道区别对待的逻辑。
不能有矛盾冲突的要求本来也无可厚非,但在我们现实的世界,存在很多弗协调(即不协调但足道)的状况;特别是在认知领域中,弗协调的状况几乎就是常态,甚至可以说是不可避免的。于大而言,不同的民族、文化、宗教信仰、社会阶层等之间,在观念和信仰上存在着某种天然的不一致。于小而言,某个认知主体或认知共同体也不可能保证其知识信念始终都协调一致、始终没有矛盾冲突。这就有个问题:在解决矛盾冲突之前,存在矛盾冲突的现阶段,我们是否真的就相信了任意陈述?显然没有。也就是说,在这种情况下,我们的理性思维所依赖的基础逻辑应当是一种可以容忍冲突,但同时又不会导致爆炸性后的逻辑。而此处所给出的弗协调认知逻辑C1D正是这样一种逻辑。
比如,当一个认知主体j因为某种原因同时相信了一个陈述及其否定,用逻辑语言可以将之描述为Bj(α∧¬α)或Bjα∧Bj¬α。如果该认知主体的基础逻辑是经典认知逻辑(即,由经典逻辑通过扩充认知算子及其相关公理和推理规则而得到的认知逻辑),由于公式(α∧¬α)→β是经典逻辑的定理,所以使用公理(14)和R2易证Bj(α∧¬α)→Bjβ和(Bjα∧Bj¬α)→Bjβ也将是定理。这两条定理的直观含义是说,如果认知主体同时相信了一个陈述及其否定,那么他在逻辑上就必须相信任意的陈述。这就意味着,若以经典认知逻辑为基础,认知主体在进行有意义的认知活动之前,这种认知的矛盾冲突必须被清除掉。否则,其结果就会导致其它所有的认知活动在逻辑上丧失了必要。
但实际的情况并非如此。即使一个认知主体接受了一个陈述及其否定,他仍然保持着足够的理性,仍然可以进行有意义的认知活动。这就是说,面对信念中的不协调,我们并没在事实上失去逻辑的理性,进而真地就去相信任意的陈述。此时,认知主体理性的基础逻辑显然不是经典认知逻辑,而是一种可以包含信念冲突且不会导致相信任意陈述的逻辑。根据推论2,上述的两个公式Bj(α∧¬α)→Bjβ和(Bjα∧Bj¬α)→Bjβ已不是C1D的定理,所以弗协调置信逻辑就具有了这种容忍认知冲突但同时又不会导致爆炸性后果机制,因而就可以作为弗协调认知理论的一种基础逻辑。
更进一步地说,以经典认知逻辑为基础不能同时相信一个陈述及其否定的原因在于:在经典认知逻辑中,公式(Bjα∧Bj¬α)没有模型;即,不存在某个认知世界w,使得(Bjα∧Bj¬α,w)=1。这是显而易见的。因为若有(Bjα∧Bj¬α,w)=1,则有(Bjα,w)=1且(Bj¬α,w)=1。而根据经典认知逻辑对否定词的赋值定义,这是不可能的。所以,公式(Bjα∧Bj¬α)在经典认知逻辑中为是不可满足式。所以,根据经典认知逻辑的要求,认知主体就不可以同时相信一个陈述及其否定。这是我们对信念系统所追求的一种理想状态;在这种理想状态中,我们的信念是协调一致的,是不存在任何矛盾冲突的。
然而,我们之所以称之为“理想状态”,就是因为在许多的实际情境中,我们很难确保认知个体或着某个认知共同体的知识或信念没有冲突。在C1D中,一般意义的矛盾律受到了限制,于是一个陈述及其否定(该否定为弗协调否定,而不是经典否定)则可以同时成立。更具体地说,根据定义2(1),C1D允许(Bjα,w)=1且 (Bj¬α,w)=1;所以根据定义 2(5),(Bjα∧Bj¬α,w)可以为 1(但不是一定为1)。也即是说,如果以弗协调置信逻辑C1D为基础,认知主体就可以相信一个陈述及其(弗协调)否定。同时,又不会因此而导致爆炸性后果,因为公式(Bjα∧Bj¬α)→Bjβ已不再是系统C1D的定理。如果以弗协调置信逻辑C1D为基础,我们就可以既容忍认知冲突,又不会在逻辑上失去理性而去相信一切。
总而言之,在知识和信念占重要地位的认知领域,出现矛盾冲突的情形几乎是以常态方式而存在的。经典认知逻辑要求我们必须要将它们解决掉,这样的要求无可厚非,也是必要的。如果这些认知的矛盾冲突可以被及时而恰当地解决,那是最理想的结果。但实际上,解决这些知识信念的矛盾冲突不仅需要耗费大量辛勤的智力活动,更重要的是也需要耗费相当长的时间。此外,还存着某些在某种层面上无需考虑其影响,也无需考虑将之解决的那种知识信念的矛盾冲突(比如,罗素悖论在初级集合论学习层面或日常生活层面上,就无需考虑其影响)。面对这些尚未解决或在一定层面上无需解决的矛盾冲突,我们在逻辑上是否真的就处于“相信一切”的混乱状态呢?显然没有。实际上,认知主体在容忍它们的状态下,仍然可以顺利地进行着理性思考,因而其基础逻辑显然就应该是一种弗协调性质的认知逻辑。弗协调多主体置信逻辑C1D可以容忍那些形如Bj(α∧¬α)、(Bjα∧Bj¬α)或(Bjα↔¬Bjα)的知识信念冲突,因而就可以为那些包含知识信念矛盾冲突的理论提供的一种可靠的基础逻辑。维特根斯坦曾经预言和期望一种可以包含矛盾的演算([13],第171页),如果把弗协调逻辑看作是这种演算的开端,那么弗协调置信逻辑或许正好展示了这种演算在信念领域的实践应用。
[1]A.I.Arruda and N.C.A.da Costa,1984,“On the relerant systemsPandP∗and some related systems”,Studia Logica,43(3):33-49.
[2]T.Burge,1978,“Buridan and epistemic paradox”,Philosophical Studies,34(1):21-35.
[3]N.C.A.da Costa and L.Dubikajtis,1997,“On Jaśkowski’s discussive logic”,in A.I.Arruda,N.C.A.daCostaandR.Chuaqui(eds.),Non-ClassicalLogic,ModelTheoryandComputability,pp.37-56,North-Holland.
[4]N.C.A.da Costa,D.Karuse and O.Bueno,2007,Paraconsistent Logics and Paraconsistency,Elsevier.
[5]S.Jaśkowski,1969,“Propositional calculus for contraditory deductive systems”,Studia Logica,24(1):143-157.
[6]J.Łukasiewicz,1971,“On the principle of contradiction in Aristotle”,Review of Methaphysics,24(3):485-509.
[7]R.K.Meyer and R.Routley,1973,“Classical relevant logics I”,Studia Logica,32(1):51-66.
[8]R.K.Meyer and R.Routley,1974,“Classical relevant logics II”,Studia Logica,33(2):183-194.
[9]G.Priest,1979,“The logic of paradox”,Journal of Philosophical Logic,8(1):219-241.
[10]G.Priest,2002,“Paraconsistent logic”,in D.M.Gabby and F.Guenthner(eds.),Handbook of Philosophical Logic,Vol.6,pp.287-393,Kluwer Acadernic Publishers.
[11]G.Priest and R.Routley,1984,“Introduction:Paraconsistent logics”,Studia Logica,43(1-2):3-16.
[12]N.A.Vasil’év,2003,“Imaginary(non-Aristotelian)logic”,translatedbyR.Vergauwen,Logique Et Analyse,46(182):127-163.
[13]夏基松,郑毓信,西方数学哲学,1986年,北京:人民出版社。
[14]张建军,逻辑悖论研究引论(修订本),2014年,北京:人民出版社。
[15]张建军等,当代逻辑哲学前沿问题研究,2014年,北京:人民出版社。
[16]张清宇,弗协调逻辑,2003年,北京:中国社会出版社。

