一种改进的分布式数据Chernoff融合方法*

田 来，吴照林，王 龙

（国防科技大学 信息通信学院，湖北 武汉 430010）

0 引 言

在设计用于战术军事应用的分布式传感系统时，一些实际的因素使假定数据输入具有统计独立性的经典算法的使用受到限制。首先，战术环境通常由传感器和数据处理节点组成，这些节点通过移动自组网连接，其网络动态变化且不可预测。由于在这些处理节点中部分数据是由融合产生的，不是直接取自传感器的数据，实际上不可能实时消除节点之间的冗余数据。其次，许多提供传感数据的现有系统不能升级产生统计独立的数据源，或提供有助于识别目标的谱系信息的数据流。最后，在这些处理节点之间具有各种主动、被动、高斯和非高斯等统计特征的传感数据是共享的，因此要在战术军事应用中实现可扩展的分布式传感系统。尤其是在存在“谣言传播”的情况下，需要用于融合各种类型的多输入数据的数据融合方法。

谱系标记[1]是一种处理谣言传播问题的方法。该方法涉及元数据的交换，该元数据表示特定传感数据的处理历史和源信息。理论上，使用这种方法可以在运行时识别冗余数据，并采用替代处理来消除冗余。但是，在实践中存在一些问题：实施谱系标记需要修改现有的产生传感数据的传感器处理系统；即使冗余数据被识别，谱系信息（元数据）也不足以从状态估计中精确消除冗余；谱系标记无法在通信带宽方面进行扩展[2]。因此，出现了协方差交叉算法来替代谱系标记方法。

协方差交叉算法是为了融合可能包含统计相关的冗余数据输入的状态估计而开发的。它的优点是并不需要各数据源之间具体的统计相关知识。后对协方差交叉算法进行推广，用于两个有任意概率密度函数的输入的融合[3]。这些突破性发展使得可扩展的分布式数据融合成为可能。虽然目前已能对任何数量的高斯输入进行融合[4]，但在更广泛的情况下，如融合任何数量的具有任意概率密度函数的输入，还没有很好的解决方案。

1 协方差交叉及其近似解

考虑融合两个统计独立的高斯概率分布状态估计的特殊情况，给出一阶和二阶矩，即均值和协方差矩阵。这种情况下，融合时使用信息过滤器[5]。由两个统计独立的状态估计的均值a、b和协方差矩阵A、B得到融合均值TE和和协方差矩阵TC：

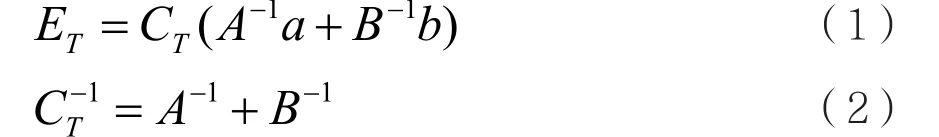
式（1）、式（2）用于早期的实时传感系统。由于它具有简单性，在输入不一定是统计独立的情况下，经常被错误地使用，导致融合结果的协方差失真，是分布式数据融合架构中谣言传播的典型问题。在多个平台上进行融合时，这种方法很难实现。因为多个平台和外部传感系统被集成到融合架构中，这些外部系统不受任何内部程序的控制。随着整合越来越多外部系统，谣言传播问题变得更加难以管控。

为了解决这个问题并实现可扩展的分布式数据融合，协方差交叉算法将高斯输入的特殊情况扩展到具有未知统计相关性的输入。协方差交叉方程对经典信息过滤器做了改进：

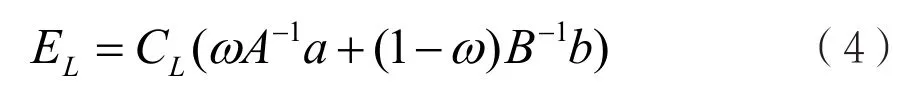
式（3）、式（4）提供的解决方案是在区间[0，1]中优化参数ω，通常是通过选择ω的值使融合协方差LC行列式最小化[3]。协方差交叉的一个重要性质是输入{,}a A和{,}b B一致时，融合解 },{LLCE 保证对任何值都一致。因此，ω的选择不需要精确，但是应该提供一个比任何一个输入协方差都小的融合协方差LC。

在一些实际应用场合中，通常要求融合2＞n个统计相关的高斯状态估计，其中每个估计由平均值和协方差矩阵},{iiVµ表示。虽然这可以通过使式（3）、式（4）迭代执行1−n次来实现，但是与文献[4]给出的解决方案相比，迭代方法产生的结果并不太理想。

式（5）、式（6）、式（7）引出对于n个iω值的优化问题，其中每个值被限制在区间[0，1]，这比式（3）、式（4）的优化问题复杂得多。在文献[4]中已证明，当输入协方差矩阵具有完全不同的特征值时，这种优化变得较为困难。因此，下面的快速近似方法被用来代替数值优化：

式（8）、式（9）中，是融合了假设统计独立的n个输入的信息矩阵。是第i个状态估计输入的信息矩阵。是通过融合除第i个输入之外的所有输入获得的信息矩阵。因此，优化参数由信息过滤器解决方案和每个输入之间的相互信息决定。就经典的信息滤波结果而言，式（8）、式（9）能够简单实时地实现更一般的协方差交叉问题。因此，现有的融合算法可以很容易地“升级”来对可能遭受谣言传播的n个输入实现协方差交叉。

2 Chernoff融合

前面讨论了原始的协方差交叉点及其对n个输入的推广。但是，在这两种情况下的算法都是限于均值和协方差矩阵指定的高斯输入。要适应任何概率密度函数的广义融合，则应以贝叶斯方程作为基础：

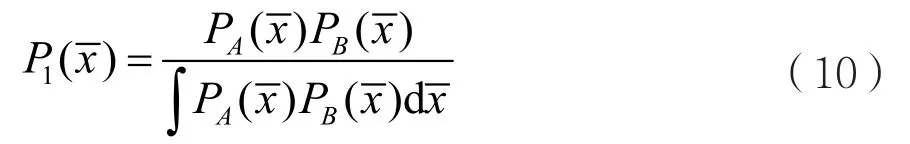
式（10）提供了假定为统计独立的两个任意概率密度函数融合的贝叶斯方程。在高斯情况下，式（10）呈现出等同于式（1）、式（2）的对数线性形式。因此，文献[3]中提出了用于融合两个具有未知相关性的任意概率密度函数的Chernoff融合：

和协方差交叉一样，式（11）中每个参数ω值都有一个解决方案。文献[3]中提出了计算参数ω的两个准则：最小化融合概率密度函数的香农熵和最小化融合概率密度函数的Chernoff信息。文献[3]中已证明，最小化香农熵等价于使高斯情形的协方差的行列式最小化。Chernoff信息标准试图找到处于输入概率密度函数“中间”的融合概率密度函数。虽然这两个标准都具有令人满意的信息理论解释，但还存在几个实际的实施问题。首先，虽然香农熵标准可以很容易地扩展到两个以上输入的情况，但是Chernoff信息扩展并不明显。其次，如果香农熵标准用于两个以上的输入，则计算复杂度取决于概率密度函数的性质。一般来说，这相当于一个多维优化问题，往往会包含许多局部最小值。因此，许多情况下可能难以实现。

用MATLAB对两个输入情况下的融合实例进行仿真，并将结果与贝叶斯融合进行比较。图1显示了对于两个概率密度函数具有相同的香农熵的关于ω的Chernoff融合解，同时给出了贝叶斯融合解作为对比。这个例子中，文献[3]的最小化准则ω的值为0.5。图2显示了香农熵不同时Chernoff融合的例子。这种情况下，计算ω的值是0.47。

3 改进的广义Chernoff融合

最终，需要开发一种处理一般融合问题的算法，即融合n个统计相关的概率密度函数。另外，为了使分布式融合实际中可应用，需要计算量较小的算法。对式（11）进行扩展，得出对于多输入的Chernoff融合的方程：

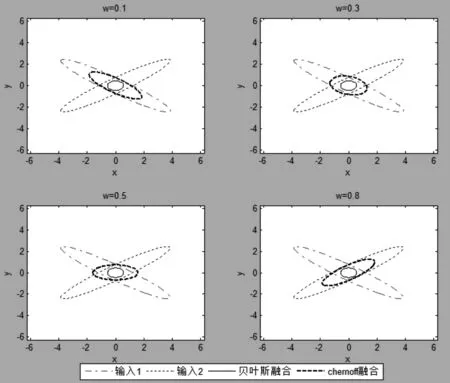
图1 不同ω取值时的Chernoff融合解（香农熵相同）

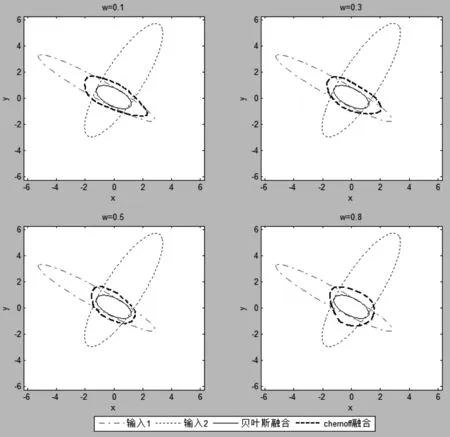
图2 不同ω取值时的Chernoff融合解（香农熵不同）

其中优化参数iω需要使用一些标准来计算。如前所述，实际中这个优化问题的实现比较复杂。

前面的研究表明，存在广义Chernoff融合问题的近似解：

（1）式（8）、式（9）中的优化参数取决于高斯分布的协方差矩阵的行列式。

（2）协方差矩阵的行列式与高斯分布的香农熵有关。

（3）式（11）中ω的“最优”值取决于输入的香农熵。

这表明了存在一个类似式（8）、式（9）的公式，是任意概率密度函数输入的香农熵的函数。首先，针对m变量高斯分布的香农熵H是根据它们的协方差给出的：

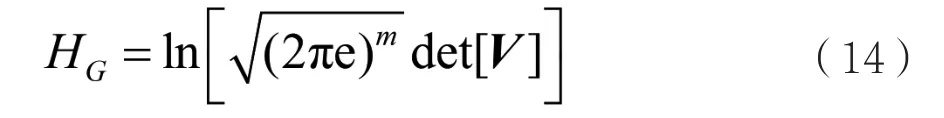
其次，行列式具有以下属性：

式（14）和式（15）结合，可以得到遵循高斯概率密度函数的协方差矩阵与其香农熵之间的关系：

这里对香农熵进行定义：BH 是所有输入的贝叶斯融合，iH是第i个输入的贝叶斯融合，iBH−是除了第i个输入的所有输入的贝叶斯融合。将式（16）代入式（8）、式（9）进行简化，得到：

和式（8）、式（9）一样，式（17）使用每个输入的相对信息含量与融合结果进行比较来计算优化参数。特别地，是加入第i个输入而导致的信息增加，则是加入除第i个输入以外的所有数据而导致的信息增加。

虽然式（17）比多参数优化要简单，但它仍然不能提供计算优化参数iω的实用方法。为了实现式（17），还需要进行以下步骤：

（1）计算每一个输入概率密度函数的香农熵Hi。

（2）计算 1+n 个贝叶斯融合解：包含所有n个输入的一个解；和另外n个包含除了第i个输入的所有输入的解。

（3）计算上一步描述的每个贝叶斯融合解的香农熵，并计算式（17）。

作为上述方法的替代方案，可以进行一些非常简单的近似来加快计算。首先，可以假设贝叶斯融合结果的香农熵等于具有最小熵的输入除以输入的数量，即可以做出以下下限近似值：

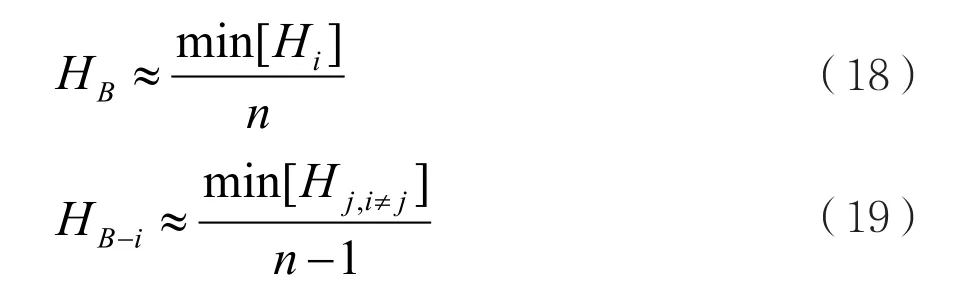
使用式（18）、式（19），可以将式（17）简化为：

式（20）提供了只有概率密度函数输入的香农熵情况下的优化参数。因此，它为广义Chernoff融合提供了一个易处理的解决方案。

为了验证其效果，用MATLAB对几个融合实例进行仿真，并将结果与使用数值优化获得的“最优”解进行比较。

图3显示了3个输入时广义Chernoff融合近似的仿真结果。得到的近似解用粗虚线示出，而数值优化结果用极粗虚线示出。为了便于比较，绘出了所有3个输入的贝叶斯融合结果。用式（20）计算以下优化参数ω1(A)=0.42、ω2(A)=0.32、ω3(A)=0.35，而数值优化得出的优化参数为ω1(I)=0.32、ω2(I)=0.32、ω3(I)=0.36。

图4提供了5个输入时广义Chernoff融合近似的仿真结果。这种情况下，计算5个输入概率密度函数的优化参数ω1(A)=0.42、ω2(A)=0.17、ω3(A)=0.18、ω4(A)=0.18、ω5(A)=0.23作为对比，数值优化的参数为 ω1(I)=0.20、ω2(I)=0.20、ω3(I)=0.12、ω4(I)=0.20、ω5(I)=0.19。

从图3、图4可以看出，尽管解决方案的值确实不同，但是解决方案彼此差别不大。与数值优化的一般问题相比，考虑到极其简单的算法，这些小的差异是可以接受的。

图3 三个输入的广义Chernoff融合

图4 五个输入的广义Chernoff融合

4 结 语

从协方差交叉算法和其扩展着手，处理多个高斯和非高斯概率密度函数的输入，开发了通用情况下的快速近似方法。该方法来源于：（1）香农熵与高斯协方差行列式之间的关系；（2）协方差交叉的快速近似方法捕获了每个输入相对于贝叶斯融合方法的相对信息量。本文的创新贡献与用于验证的数值优化相比较，发现广义Chernoff融合产生了非常相似的解。以后的工作将研究这种近似方法在极端情况下如输入概率密度函数的香农熵都非常大或非常小的情况下的表现。

[1] Ceruti M G,Wright T L,Powers B J,et al.Data Pedigree and Strategies for Dynamic Level-One Sensor Data Fusion[C].Information Fusion,2006 9th International Conference,2006:1-5.

[2] Nicholson D,Lloyd C M,Julier S J,et al.Scalable Distributed Data Fusion[C].Information Fusion,2002 Proceedings of the Fifth International Conference,2002:630-635.

[3] Hurley M B.An Information Theoretic Justification for Covariance Intersection and Its Generalization[C].Information Fusion,2002 Proceedings of the Fifth International Conference,2002:505-511.

[4] Franken D,Hupper A.Improved Fast Covariance Intersection for Distributed Data Fusion[C].Information Fusion,2005 8th International Conference,2005:25-28.

[5] BU Xiang-yi.Research on Moving Target Tracking and Information Filtering in Complex Building Environment[C].2016 3rd International Conference on Materials Engineering,Manufacturing Technology and Control,2016:56-59.