一类Caputo分数阶脉冲微分方程的反周期边值问题
宋 姝, 周碧波, 张玲玲
(1. 山西工程职业技术学院 基础部, 山西 太原 030009; 2. 吕梁学院 数学系, 山西 吕梁 033006;3. 太原理工大学 数学学院, 山西太原 030024)
分数阶微积分是经典的整数阶微积分的拓展,有着与整数阶微积分几乎相同的发展史. 20世纪80年代初, Bagley和Torvik成功运用分数阶导数描述阻尼. 至此, 分数阶微积分方程因其具有遗传性和记忆性, 得到许多物理工程研究者的重视. 目前, 分数阶微积分理论与方法已经被广泛地应用到自然科学领域与社会科学的各个领域, 如自动控制、 信号处理、 复杂粘性材料力学本构关系、 天气预报、 地震奇异性分析等, 具体可参见文献[1-4]. 随着科学技术的发展, 药物的药效、 生物种群中物种的出生、 作物的施肥等过程中出现的反周期问题受到专家学者们的关注. 此外, 含脉冲的微分方程是刻画瞬时突变现象的基本工具. 随着整数阶导数推广到分数阶导数, 人们自然而然地想到分数阶脉冲微分方程反周期边值问题.
文献[5]考察了如下一类分数阶微分方程的反周期边值问题

文献[6]考察了如下一类非线性Caputo分数阶微分方程的反周期边值问题
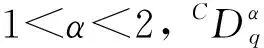
文献[7]讨论了一类关于1 式中:f∶J×R→R是一个连续函数,Ik,Jk∶R→R,α>0,β>0, 通过应用Krasonselskii’s不动点定理和压缩映像原理, 得到了这类边值问题解的存在性和唯一性的充分条件. 受以上文献的启发, 本文研究如下非线性分数阶脉冲微分方程 (1) 为叙述问题方便, 给出如下符号和定义: 令J∶=[0,T], 集合 D∶={t1,t2,…,tp}⊂(0,T), 并且满足0 J0∶=[0,t1], J1∶=(t1,t2],…,Jp-1∶=(tp-1,tp], Jp∶=(tp,T], 并且J′∶=JD. 定义 PC[J,R]∶={u|u∶J→R, u(t)在t≠tk连续,u(t)在t=tk左连续, 在 定义1[8]若u∈PCα-1[J,R]且满足式(1), 则称u是α阶脉冲微分方程反周期边值问题(1)的一个解. 引理1[5]令α>0,β>0,f∈C[0,T], 则下列结论成立: 引理2[5]令α∈R+N, 则有 引理4对给定的函数y∈C[0,T], 若u∈PCα-1[J,R]是下列分数阶脉冲微分方程反周期边值问题的解: (2) 当且仅当u是下列脉冲积分方程的一个解: (3) 证明必要性: 由分数阶积分的定义, 分数阶导数的定义, 见文献[9], 以及引理1、 引理2和引理3, 通过常规计算可得式(3). 另外再对式(3)两边分别取α次分数阶导数, 必要性显然成立. 首先在PCα-1[J,R]上定义一个算子A, 对∀u∈PCα-1[J,R], 令算子 (4) 为了方便表示, 令 定理1假设下列条件满足: H1)f在[0,T]×R×R上连续,Ik∈C[R,R],Jk∈C[R,R]. |Ik(u)-Ik(v)| |Jk(u)-Jk(v)|≤K3|u-v|. 则分数阶脉冲微分方程反周期边值问题(1)有唯一解. 证明由条件H1)以及算子Au的表达式可知, 算子Au在J′上连续, 另外由引理2, 引理3可得 (5) 对∀u,v∈PC[J,R], ∀t∈Jk, 记 由H2)可得 所以, 有 ‖Au-Av‖∞≤ (6) 另外, 对∀t∈Jk, 由式(5)和H2)同理可得 (2K1S+K3G)‖u-v‖B. (7) 由式(6)和式(7)可知 ‖Au-Av‖B=max{‖Au-Av‖∞, 再由定理1中的条件H3)可知L<1, 所以算子A在PCα-1[J,R]上是一个压缩映射, 由压缩映像原理可知, 算子A在PCα-1[J,R]有唯一不动点, 即反周期边值问题(1)有唯一解. 定理2假设以下条件满足: H4) 若存在连续的非减函数φ∶[0,∞]→(0,∞)和函数h(t)∈C[0,T], 满足对∀t∈J,u∈PCα-1[J,R], 有 且存在非负常数L1,L2对∀t∈J,u∈PCα-1[J,R], 有 |Ik(u)|≤L1, |Jk(u)|≤L2. 则反周期边值问题(1)在PCα-1[J,R]上至少有一个解. 1) 先证明A∶E→E有界. 对∀u∈E, ∀t∈Jk, 由定理2的条件H4)和式(4)可得 (8) 由式(8)可知 (9) 并且对∀u∈E, ∀t∈Jk, 由式(5)及定理2条件H4), 可得 (10) 通式(9)和式(10)及H5)可知 max{Mφ(r)R+p(L1+L2T),Mφ(r)S+ GL2}≤r, 所以, 算子A∶E→E有界. 2) 证明A∶E→E全连续. 对∀u∈E, 由式(4)可知 所以, 对∀u∈E, ∀t1,t2∈Jk, 有 (Mφ(r)H+pL2)|t2-t1|. (10) 由式(11)可知, 当t1→t2时, |Au(t2)-Au(t1)|→0. 再者对∀u∈E, ∀t1,t2∈Jk, 有 3) 令V={u∈E|u=μAu,0<μ<1}, 证集合V有界. 对∀u∈V, ∀t∈Jk, 由式(9)可得 |u(t)|=μ|(Au)(t)|≤μMφ(r)R+ 即有 (12) 对∀u∈V, ∀t∈Jk, 由式(10), 用类似方法可得 (13) 由式(12)和式(13)可知 μMφ(r)S+μGL2}. 所以, 集合V={u∈E|u-μAu,0<μ<1}有界, 由Schaefer不动点定理[10]可知, 算子A在空间E上至少有一个不动点, 即反周期边值问题(1)在PC[J,R]上至少存在一个解. 例1考虑如下脉冲微分方程的反周期边值问题: (14) 且有 由上述可知, 条件H1),H2),H3)均满足, 因此由定理1可知脉冲微分方程的反周期边值问题(14)有唯一解. 例2考虑如下关于α=1.5的脉冲微分方程的反周期边值问题: (15) 选取r=14>max{11.9,13.1}, 则满足式H5), 因此由定理2可知, 脉冲微分方程反周期边值问题(15)至少有一个解.
1 预备知识






2 主要结果





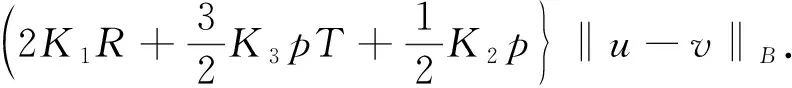

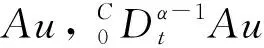

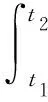

3 算 例




