第二型曲面积分的中值定理

广西民族大学理学院 张晓呵

积分中值定理体系庞大，但仍然有大量数学学者在研究，在华东师范版和刘玉琏的数学分析中给出了积分中值定理和积分第二中值定理的定义和证明后，对于其在曲线和曲面上的形式并未明确，目前主要在连续型曲面上提出了相关假设。我们知道第二型曲面积分的不等式性质一般不成立，所以一般情况下,第二型曲面积分的中值定理亦不再成立，欲使其成立，那么对曲面的要求将更加严格，本文便给出了这样的曲面，同时将中值定理的“连续性”弱化为“介值性”和“可积性”,并在其上定义和证明了第二型曲面积分的中值定理。

一、定义和定理

欲使第二型曲面积分的中值定理成立，那么对曲面的要求将更加严格，以下我们将对这类曲面进行讨论。

1．法线单向曲面

定义2.11 设有光滑曲面C，任意包含于曲面C的小曲面Ci的法向量与z轴所呈夹角为θ。我们称曲面C为法线单向曲面，如果cosθ不变号,显然,法线单向曲面有以下性质：

性质2.11 设曲面C为法线单向曲面，f为定义在C上的函数，且f(x,y,z)≥0，(x,y,z)∈C，若f在C上第二型可积，则有：

性质2.12 设曲面C为法线单向曲面，f与g为定义C在上的函数，且f与g在C上第二型可积，若f(x,y,z)≤g(x,y,z)，(x,y,z)∈C，则有：

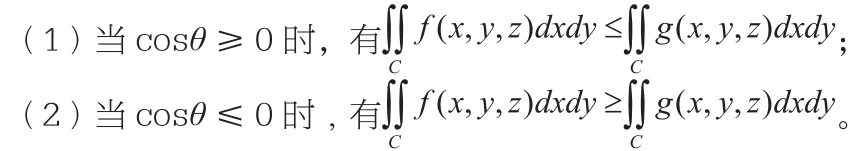
性质2.13 设曲面C为法线单向曲面，f为定义在C上的函数，且第二型可积，

（1）当cosθ≥0时，曲面C至少存在一个小曲面块Ci，有f(x,y,z)＞ 0，(x,y,z)∈ Ci；

（2）当cosθ≤0时，曲面C至少存在一个小曲面块Ci，有f(x,y,z)＜ 0，(x,y,z)∈ Ci。

证明：只证当cosθ≥0时的情形，当cosθ≤0时的情形可类似证明。

假设任意包含于曲面C的小曲面块Ci上均为f(x,y,z)≤0，由性可得），显然与条件矛盾。

2．介值性定理

我们先给出定义，在曲面上的函数的介值性的定义。

定义2.21 设f(x,y,z)是定义在曲面C上的函数，记：

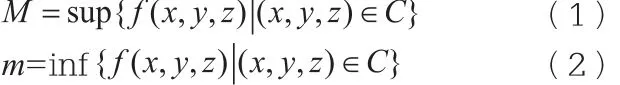
我们称f在C上是可介值的，如果任意的实数α:m＜α＜M，在曲面上至少存在一点 ，使得：

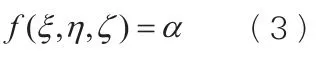
事实上，函数的介值性是弱于连续性的，若f在C上是连续的，则f在C上可介值的，反之却不一定成立。

3．曲面积分的相关性质

性质2.31 若曲面C由小曲面块C1,C2…Ck接连而成，且

证明见参考文献[1]第二型曲面积分的性质。

性质2.32（有界性） 设曲面C为法线单向曲面，f为定义在C上的函数，若f在C上第二型可积，则f(x,y,z)在C必定有界，其中C取上侧。

证明：用反证法。若f在C上无界，则对于C上的任意分割T，必存在属于T的某个小曲面块Ck，f在Ck上无界，在i≠k的各个小曲面块Ci上任意取定 ，并记：

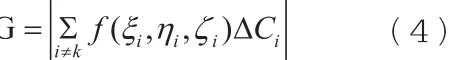
现对任意大的正数M，由于f在Ck上无界，故存在 ，使得：

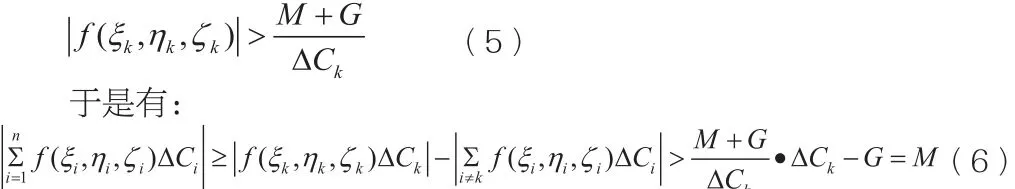
由此可见，对于无论多么小的 ，按照上述方法选取点集时，总能使积分和的绝对值大于任何预先给定的正数，这与函数f(x,y,z)在曲面C第二型可积矛盾。

二、主要结果

定义3.1 设C是法线单向曲面，f，g为定义在C上的函数，且满足如下条件：

（1）f(x,y,z),g(x,y,z)在曲面C上第二型可积；

（2）f(x,y,z)是可介值的；

（3）g(x,y,z)在c上不变号；

则至少存在一点 使得：

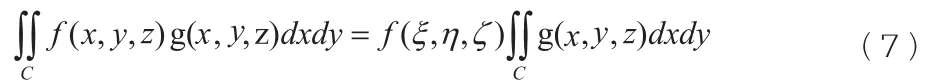
其中C取上侧。由条件3），不妨设g(x,y,z)≥0，(x,y,z)∈C，这时有：

由此我们便得出法线单向曲面上的第二型曲面积分中值定理。