结构面破坏时单裂隙变形及渗流规律研究

曹 成，柴军瑞，覃 源，许增光，谈 然

(西安理工大学 西北旱区生态水利工程国家重点实验室培训基地，陕西 西安 710048)

流体在岩体裂隙中的渗流规律以及流体与应力的耦合作用，一直都是影响地下能源开采与储存、核废料处理、地下空间开发等工程安全性和可行性的因素。一般认为岩石的渗透系数很小，可以忽略。因此在复杂应力下，流体在单裂隙中的渗流规律一直是学者们关注的重点[1-3]。

立方定理一直是试验过程中描述裂隙中流体渗流规律的重要理论方法，然而自然条件下裂隙结构面的几何形貌十分复杂，由于粗糙度、接触面积和曲折效应等因素的影响，使得立方定理所忽略的流体非线性越来越明显[4-5]，与试验结果相比立方定理往往高估或低估了裂隙的过流能力[6]。粗糙度越大，流体的非线性越严重[7]，渗透系数会随接触面积的增大而明显降低[8-9]，并且在高水头作用下，流体雷诺数较高时惯性力的影响也不容忽略，较大的惯性力往往会引起流体的非线性变化[9-10]。

在法向应力的作用下，裂隙结构面的接触面积增大，渗流通道因结构面变形而减小，所以渗透系数一般都会随法向应力的增大而减小[11-12]。然而有试验证实，即使法向应力高达160 MPa，仍有渗流现象存在[13]。此外，渗透系数随法向应力的变化与裂隙结构面刚度和渗流通道的连通性密切相关[14]。在剪切作用下，结构面的几何形貌会发生变化，结构面破坏之前，由于裂隙上、下表面之间的错位，结构面凹凸体之间的爬坡效应使得接触面积不断变化。结构面破坏之后，接触面积则因结构面破坏形态和填充物的分布而变化，此外粗糙度也因结构面的破坏而降低[15-16]。机械隙宽(em)在剪切过程中会有大幅度的增加，因此渗透系数在剪切过程中会大幅增加[9-10,15]，由于流体的各向异性，剪切过程中不同方向的渗流系数和流速变化并不相同[17-18]。此外，现已有诸多的研究成果描述了剪切过程中em与立方定理求得的水力隙宽(eh)之间的关系，并且对剪切过程中的渗流规律进行预测。Olsson等[16]利用结构面粗糙度JRC值预测剪切过程中eh和em的变化规律；Zimmerman等[19]研究了隙宽标准差和接触面积对eh和em的影响；Xiong等[10]发现，剪切过程中惯性力对渗流有显著的影响，并在Zimmerman等[19]研究的基础上分析了雷诺数对eh和em的影响；Matsuki等[20]发现流体运动方向与剪切方向的夹角会对eh和em产生影响。

结构面破坏所产生的碎屑填充物在剪切过程中会对结构面的强度和流体渗流产生不容忽视的影响[13-15]，但目前针对剪切过程中结构面大规模破坏的试验较少。为此，本研究在前人研究的基础上，利用新型岩石节理直剪-渗流耦合仪器，分析规则齿结构面在不同咬合状态下剪切破坏过程中裂隙结构面强度和变形的变化规律，探讨完全咬合状态下不同高水头作用时的渗流变化特性，以期为描述裂隙中流体的渗流规律提供支持。

1 单裂隙应力-渗流耦合试验

1.1 试验设备

试验仪器采用TJXW-600型微机控制岩石节理直剪渗流耦合系统(图1)。仪器法向和切向荷载均由伺服油源提供。法向、切向最大荷载为600 kN，荷载测量精度为示值的±1%，加载方式有荷载控制加载和位移控制加载。位移由拉线位移传感器测得，法向位移精度为0.003 mm，切向位移精度为0.04 mm。应力、应变和位移等信号由Multli-05全数字多通道闭环测控仪控制。水压由与水箱连接的高压氮气瓶提供，最大水压力为3 MPa。剪切盒分为上、下两部分，剪切过程中下试件固定，上试件移动，最大剪切位移为35 mm。剪切盒通过在安装过程中对密封圈挤压实现高度密封，在高压渗流的作用下无漏水情况。剪切盒剖面内部结构示意图及剖面实物图见图2和图3。

1.2 试验试件

考虑到天然岩石制样的复杂性，试验采用α型半水高强石膏制作类岩试件，石膏、水、缓凝剂的质量比为1∶0.25∶0.005，试件直径200 mm、高75 mm。试件结构面为规则齿状，剪切方向起伏角为15°。试件力学参数为：密度1.79 kg/m3，抗压强度47.82 MPa，弹性模量2.57 GPa，泊松比0.3 μ。

图2 剪切盒内部构造图Fig.2 Internal structure of shear box图3 剪切盒A-A断面实物图Fig.3 Sectional view A-A of shear box

1.3 试验过程

试验过程中法向边界条件为常法向荷载边界条件(CNL)，法向应力达到设定值并稳定时通水，待出水流量稳定之后开始剪切。剪切速率为15 mm/min，当剪切位移达到28 mm时试验结束。法向位移和剪切位移由拉线式位移传感器测定，法向应力和剪切应力由压阻式应变传感器测定，流量由出口处的电子称测得，所有数据汇总到计算机内可直接得到不同时刻的位移、应力及累计流量，进而可以确定不同剪切位移时法向位移、剪切应力以及流量的变化。由于直接测得的流量单位为g/s，根据水温为25 ℃时水的密度为0.997 g/cm3[21]，将流量单位转换为cm3/s。此外，由于直接测得的流量为累计流量，通过裂隙的实际流量应为各时刻的流量差。试件咬合状态分完全咬合状态和非完全咬合状态(图4)，试验时法向应力(σ)为1.91 MPa，水压(p)为0.6 MPa。随后在完全咬合的情况下，调整水压为0.4，0.6和0.8 MPa。

图4 试验开始前上、下试件的咬合状态Fig.4 Occlusion situation of upper and lower specimens before test

2 结果与分析

2.1 强度与变形分析

完全和非完全咬合状态下，上、下试件的破损情况及结构面剪切强度(τ)和法向位移(Δu)随剪切位移(δ)的变化曲线见图5和图6。由图5可知，试验结束后完全咬合状态下的上、下试件结构齿被充分破坏，碎屑填充物充分覆盖于结构面，结构面基本没有残余齿的痕迹，表面粗糙度和接触面积主要由碎屑填充物的堆积形式决定；非完全咬合状态上、下试件残余齿明显，碎屑填充物并未完全覆盖整个结构面，齿的破坏程度较低。

由图6可以看出，完全咬合和非完全咬合2种状态下，剪切强度曲线有明显的峰值阶段，峰值之前剪切强度几乎呈线性增加，曲线斜率即节理的初始剪切刚度[22]。由于应力扰动，结构齿之间的咬合更加紧密，初始阶段Δu出现负值，即剪缩阶段；随后Δu由于上、下结构齿之间的爬坡效应而开始增大，进入剪胀阶段，剪切强度也逐渐增大，直到结构面初次破坏，此时剪切强度达到峰值。

A.完全咬合状态上试件;B.完全咬合状态下试件;C.非完全咬合状态上试件;D.非完全咬合状态下试件 A.Upper specimen of fully occlusion;B.Lower specimen of fully occlusion C.Upper specimen of un-fully occlusion;D.Lower specimen of un-fully occlusion图5 试验结束后上、下试件的破损情况Fig.5 Crushed situations of upper and lower specimens after shear test

图6 剪切强度和法向位移随剪切位移的变化曲线Fig.6 Evolution of shear stress and normal displacement with shear displacement

由图6可知，对于完全咬合状态，当剪切位移δ=3.7 mm时，剪切强度达到峰值(τpeak=6.77 MPa)，随后剪切强度迅速降低。由于残余齿的第二次咬合，当δ=4.41 mm时剪切强度达到第2次峰值。由于碎屑填充物以及残余齿的破坏，当δ大于4.41 mm后剪切强度曲线进入软化阶段，当δ大于9.19 mm后进入残余阶段。结构面破坏之后法向位移的增加主要由碎屑填充物在残余齿之间的移动引起，随着碎屑填充物被研磨以及残余齿被进一步的破坏，法向位移逐渐趋于稳定值，试验结束后法向位移增加0.58 mm。

由图6还可知，对于非完全咬合状态，由于结构齿之间的咬合程度低，结构面初次破坏后残余齿较为完整。当δ=3.56 mm时剪切强度达到第一阶段峰值(τpeak 1st=4.72 MPa)，随后由于残余齿再次咬合，剪切强度曲线呈波动状态，并在δ=12.61 mm时剪切强度达到第二阶段峰值(τpeak 2nd=2.78 MPa)；在δ=22.76 mm时剪切强度达到第三阶段峰值(τpeak 3rd=2.89 MPa)。由于残余齿的咬合程度低，碎屑填充物产生量较少，使得在第二、第三峰值阶段时残余齿的破坏程度低，不足以对峰值剪切强度产生影响，因此第二、第三阶段的剪切强度峰值相差不大。法向位移在结构面破坏之后由于残余齿的再次咬合和破坏而降低，并由于残余齿之间的爬坡效应而增加，导致法向位移曲线呈波动状，但总体上由于残余齿和碎屑填充物的破坏，试验结束后法向位移减小了0.68 mm。

2.2 渗流规律分析

以完全咬合状态为基础，分析水压(p)分别为0.4，0.6和0.8 MPa时的裂隙渗流规律。用立方定理描述不可压缩流体以层流状态通过光滑平行板裂隙时的运动规律,现已广泛地应用到试验研究之中[4-6]。当水流状态为辐向流时，立方定理公式为[1,12,23]：

Q=A·Δh·e3，

(1)

(2)

式中：Δh为水头差；e为隙宽;π为常数;g为重力加速度，取9.81 m/s2；υ为流体运动黏滞系数；r0为裂隙外半径，本试验外半径取试件半径，即100 mm；ri为中心注水孔半径，本试验注水孔半径为4 mm。

此外，本研究推导了一种新的辐向流立方定理公式，推导过程如下：将计算区域内夹角为单位角度θ的扇形区域等效为宽度为单位宽度b的矩形区域，如图7所示。

则单位扇形区域的立方定理公式可以表示为：

(3)

式中：qθ为通过单位扇形区域的渗流量，r为试件半径。

将公式(3)积分到整个圆形区域，即可得到一种新的辐向流立方定理公式：

(4)

式中：θ为扇形计算区域夹角。

剪切过程中机械隙宽(em)可由下式确定[15]:

em=e0-un+Δun。

(5)

式中：e0为初始隙宽，un为法向应力引起的裂隙闭合量，Δun为剪胀引起的隙宽增量。

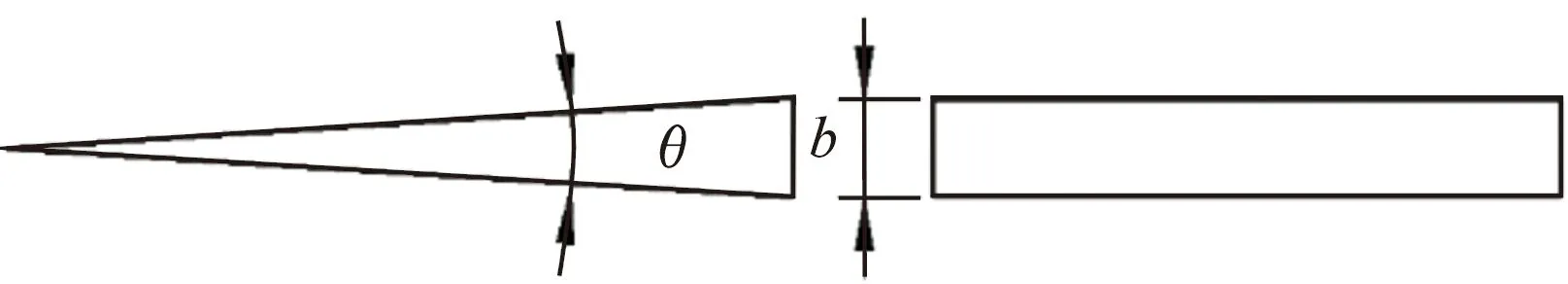
图7 计算区域等效示意图Fig.7 Schematic of equivalent treatment of computational domain

本试验忽略剪缩阶段法向位移的变化，在常法向力作用下，剪切过程中un等于0[10]；在分析和比较中假定初始隙宽e0为0，初始流量为0，Δun即Δu由试验测得，因此测得的法向位移Δu即为机械隙宽em。以法向应力为1.91 MPa、水压(p)0.6 MPa为例，由公式(1)、(4)计算得到的流量(Q)与机械隙宽(em)的关系以及试验结果中流量(Q)与机械隙宽(em)关系的对比见图8。

图8 流量(Q)计算结果和试验结果与机械隙宽(em)关系Fig.8 Relation between calculated and experimental values of flow rate (Q) and mechanical aperture (em)

从图8可以看出，与公式(1)相比，公式(4)计算得到的流量(Q)更加接近试验数据，但公式(4)仍然高估了裂隙的过流能力，使得试验值与计算值之间有一定的差异。结构面破坏之前，齿槽的分布不是辐射状，平行齿槽方向阻力小，大部分水流顺齿槽方向通过裂隙，这一部分流量无法确定，公式(4)对这一现象也无法进行修正，导致其计算值与试验结果的差异。随后由于结构齿被大规模破坏以及碎屑填充物的分布，使得水流受齿槽的影响减小并逐渐呈现出辐射状，此时试验结果开始逼近公式(4)计算值，但由于公式(4)未考虑粗糙度和结构面接触面积变化引起的非线性，使得其计算值与试验结果仍有差距。

为分析式(4)计算流量与试验结果之间的差距随机械隙宽(em)和剪切位移(δ)的变化规律，设:

ΔQ=QEq 4-QExp。

(6)

式中：ΔQ为公式(4)计算流量与试验测定流量的差值，QEq 4为公式(4)计算得到的流量值，QExp为试验测得的流量值。

ΔQ在不同水压下随机械隙宽和剪切位移的变化曲线见图9。图9表明，由于水压的增大，水流惯性力引起的非线性使得ΔQ增大，ΔQ最大达到41.5 cm3/s，当水压从0.4 MPa增大到0.6和0.8 MPa时，ΔQ分别增加5和8.2 cm3/s。

从图9可以看出，ΔQ随着em的增大而增大，并且在em高于0.35 mm后ΔQ快速增大，这是因为机械隙宽越大，粗糙度、接触面积和碎屑填充物等因素对流态的影响越复杂，使得水流的非线性变化更为显著，导致ΔQ加速增大。

从图9还可看出，随着剪切位移的增加，ΔQ先迅速增加之后趋于稳定，ΔQ的增加主要集中在结构面破坏之前以及剪切强度残余阶段。原因在于，结构面破坏之前水流的非完全轴对称性，使得试验结果偏离公式(4)辐向流的假定，结构面破坏之后碎屑填充物和残余齿不断改变结构面粗糙度和接触面积，使得ΔQ持续增大。但随着剪切过程中碎屑填充物被研磨并充分填充到残余齿槽中，结构面粗糙度降低，接触面积趋于稳定，ΔQ也逐渐趋于稳定。

图9 不同水压下流量计算结果与试验测定流量差值随机械隙宽与剪切位移的变化Fig.9 Difference in flow rate between experimental value and mechanical aperture and shear displacement under different inlet pressures

为了分析结构面破坏之前，水流垂直于齿槽方向通过裂隙时的流动状态，通过建立二维数值计算模型，分析剪切位移δ为1和2 mm以及峰值位移时，垂直齿槽方向最大横断面处水流运动规律。初始状态下垂直齿槽方向最大横断面处水流流动示意图见图10，流动方向分+x和-x2个方向，现以+x方向为例进行分析，其中初始机械隙宽由初始流量通过公式(4)反算得到。

图10 平行于剪切方向最大横截面水流的流向Fig.10 Flow direction in the maximum cross section paralleling to shear direction

以水压0.6 MPa为例，+x向各剪切位移处流线分布以及各横截面流速分布见图11。从图11可以看出，水流通过齿后，由于结构面突变会产生水流漩涡，此外比较图11-A、B和C可以发现，随着机械隙宽的增大，漩涡所占空间越来越大。

从图12可以看出，随着剪切位移的增加，漩涡内部流速先增后减再增再减，当剪切位移约为2.5 mm时，漩涡内部流速较低，最低达0.56 m/s。这说明结构面破坏之前，随着剪切位移的增加，机械隙宽不断增加，水流漩涡也不断增大，但水流漩涡会束窄有效渗流通道，使得立方定理通过em描述裂隙渗流规律时会夸大裂隙的过流能力，从而造成计算结果与试验结果的偏差。

图11 +x流向不同剪切位移处的流线分布Fig.11 Distribution of stream line in +x direction with different shear displacements

图12 +x流向不同截断面流速的分布Fig.12 Evolution of fluid flow velocity of different vertical profiles in +x direction

根据公式(4)可得到裂隙的水力隙宽(eh)以及裂隙的渗透系数(K)为:

(7)

(8)

不同水压下渗透系数随剪切位移的变化曲线见图13，不同水压下机械隙宽与水力隙宽的比值随剪切位移的变化曲线见图14。从图13可以看出，随着剪切位移的增加，K呈增加趋势，K在剪切过程中分两个阶段增大，剪切初始阶段K增量较大，随后逐渐减小并趋于定值，最大可达到2.42 cm/s。由于惯性力的影响，K随水压的增大而降低，当水压从0.4 MPa增大到0.6和0.8 MPa时，K分别降低0.27和0.47 cm/s。

图13 不同水压下渗透系数随剪切位移变化曲线Fig.13 Evolution of hydraulic conductivity under different hydraulic pressures during shear图14 不同水压下em/eh随剪切位移变化曲线Fig.14 Relationship between mechanical aperture and hydraulic aperture under different hydraulic pressures

从图14可以看出，随着剪切位移的增加，em/eh值先增加后降低，em/eh值最高点对应的剪切位移为峰值剪切位移。由于剪切过程中立方定理一直高估裂隙的过流能力，使得em/eh值一直大于1。结构面破坏之前em/eh值不断增大有两方面原因：一方面由于水流大部分顺齿槽通过裂隙，并非公式(4)中的完全轴对称辐向流状态，使得计算得到的eh和实测得到的em相差较大；另一方面当水流垂直于齿槽通过裂隙时，由于水流漩涡束窄了有效渗流通道，使得eh的增量小于em的增量。结构面破坏之后由于齿的破坏及填充物作用使得水流形态更加接近辐向流，并且粗糙度降低，导致em/eh值开始降低。由于惯性力的影响em/eh最大值会随着水压的增大而增大，最大可达1.67。水压从0.4 MPa增大到0.6和0.8 MPa时，em/eh值分别增加0.04和0.06。

3 结 论

为了研究裂隙结构面发生大规模破坏时，结构面强度变形和渗流变化规律。本研究在常法向应力(CNL)条件下，对在完全咬合和非完全咬合状态下规则齿结构面进行了剪切-渗流耦合试验，分析裂隙强度变形规律。利用本研究新推导的辐向流立方定理公式，分析了完全咬合状态下不同水压作用时裂隙的渗流规律，得到以下结论：

1)对于完全咬合状态，剪切强度曲线有明显的峰值，当剪切位移δ=3.7 mm时，剪切强度达到峰值，为6.77 MPa，随后剪切强度曲线进入软化阶段和残余阶段。对于非完全咬合状态，剪切强度曲线呈波动变化，出现3次峰值，依次为4.72，2.78和2.89 MPa。两种咬合状态下法向位移都会在剪切初始阶段出现剪缩现象，完全咬合状态下法向位移呈先快后慢两个阶段增加，试验结束后法向位移增加0.58 mm；非完全咬合状态下法向位移呈波动状减小，试验结束后法向位移降低0.68 mm。

2)本研究新推导的辐向流立方定理公式的计算结果更加接近试验结果，但由于公式未考虑结构面破坏之前水流的非完全轴对称性流动、粗糙度和接触面积的变化以及水流漩涡对有效渗流通道的影响，使得ΔQ最大达41.5 cm3/s，并且ΔQ的增量主要集中在结构面破坏之前以及剪切强度残余阶段。此外，机械隙宽越大，ΔQ越大。剪切强度软化阶段由于结构面粗糙度降低，接触面积趋于稳定，ΔQ逐渐减小并趋于稳定。

3)剪切过程中裂隙渗透系数K呈先快后慢两个阶段增加，最大可达2.42 cm/s。em/eh值在结构面破坏之前不断增大，最大达1.67。裂隙结构面破坏之后em/eh值降低，但由于公式(4)总体上高估了裂隙的过流能力，em/eh值一直大于1。

4)水压越大，惯性力引起的水流非线性作用越明显，ΔQ、K、em/eh值都受到水压的影响。当水压从0.4 MPa增大到0.6和0.8 MPa时，ΔQ分别增加5和8.2 cm3/s，K分别降低0.27和0.47 cm/s，em/eh分别增加0.04和0.06。