基于能量有限元法和虚拟模态综合法的高频冲击响应分析方法
陈兆林,杨智春,*,王用岩,张新平
1. 西北工业大学 航空学院,西安 710072 2. 航空工业成都飞机设计研究所,成都 610091 3. 航空工业陕西飞机工业(集团)公司设计院,汉中 723213
在航空航天等工程领域中,冲击载荷普遍存在。例如导弹发射[1],舰载机弹射起飞和降落[2],航天器采用爆炸螺栓进行级间分离[3-4]等,都会对结构施加短时、高幅值的冲击载荷,使结构产生包含高频成分在内的瞬态响应,造成结构尤其是敏感仪器和电子设备的故障或损伤,影响航空航天飞行器的正常工作。因此,发展高效的分析方法以求解结构在高频冲击载荷作用下的瞬态响应,具有明确的工程应用背景和意义。
在现有的冲击响应分析方法中,有限元法(Finite Element Method, FEM)最为成熟且应用广泛[5-6],常见的商业有限元软件基本都可以进行冲击响应分析。但是对于高频冲击响应分析问题,FEM却具有局限性。这是因为FEM模型需要满足一个波长内至少6个单元,而在高频段结构振动的波长很小,FEM模型就需要划分非常细密的网格,导致模型规模过大,计算成本过高[7]。
为了进行高频冲击响应分析,Dalton[8-9]将统计能量(Statistical Energy Analysis, SEA)法和虚拟模态综合(Virtual Mode Synthesis and Simulation, VMSS)法相结合,提出了SEA-VMSS法,并应用该方法分析了某装甲车在冲击载荷作用下控制舱的高频响应[10],通过与试验测得的加速度冲击响应谱进行对比,验证了该方法的有效性。近年来,国内也开展了SEA-VMSS法的相关研究工作。杨博[2]采用SEA-VMSS法预测了舰船在冲击载荷作用下结构的响应和舱室内部的噪声,发现冲击载荷的类型和作用时间对结构响应幅值和舱室噪声都有很大影响。王军评等[3]采用SEA-VMSS法对某航天器的部分舱段在爆炸分离时的冲击响应进行了分析,发现结构上各个位置的加速度响应谱都含有较高的频率成分,且加速度的幅值随着与冲击源距离的增加而减小。彭志刚[4]以某卫星平台为研究对象,采用SEA-VMSS法分析了星箭分离时卫星不同部位的冲击响应谱,研究了结构的材料属性、爆炸分离方式等因素对冲击响应谱的影响。从上述研究中可以看出,SEA-VMSS法综合了SEA适用于高频稳态分析而VMSS适用于瞬态分析的优点,成为高频冲击响应分析的高效途径。但是,由于SEA只能获得一个子系统的平均响应,不能得到响应在子系统内部的空间变化,导致SEA-VMSS法只能获得一个子系统的平均冲击响应,不能分析子系统内部某一点的冲击响应。
为了克服SEA-VMSS法的上述缺点,发展新的高频冲击响应分析方法是必要的。能量有限元法(Energy Finite Element Method, EFEM)是近年来发展的另外一种适用于高频稳态分析的新方法。EFEM以时空平均的能量密度为变量,具有模型简单、求解迅速的优点,而且能够得到子系统内部任一点的响应。对该方法的研究始于20世纪80年代,Nefske和Sung[11]提出时间平均能量强度正比于时间平均能量密度的梯度,并根据此假设推导得到类似于热传导方程的能量密度控制方程。Wohlever和Bernhard[12-13]从杆的纵向振动和梁的横向振动方程出发,证明了Nefske和Sung[11]的假设,成功将EFEM应用于求解杆、梁模型的高频振动响应。Bouthier和Bernhard[14-16]以时间和空间平均的能量密度为变量,推导得到薄膜、平板结构的能量密度控制方程并进行求解。上述研究中,载荷均为单点简谐激励,Han等[17-18]计算了分布载荷作用下梁和板的输入功率,并发展了相应的EFEM。在考虑热效应的EFEM研究方面,Zhang等[19]建立了受热梁结构的能量密度控制方程。Wang等[20]将Zhang等[19]的方法推广到受热平板模型中,并考虑了非均匀温度场的影响。经过科研工作者的努力,EFEM在高频响应分析领域的应用越来越广泛。但是,EFEM仅适用于稳态分析,不能进行冲击载荷作用下的高频瞬态分析。
为了分析结构在高频冲击载荷作用下的瞬态响应,本文通过理论推导,将EFEM和VMSS相结合,提出了EFEM-VMSS法,并通过算例验证了该方法在高频冲击响应分析方面的有效性及其相对于FEM和SEA-VMSS法的优点。
1 EFEM-VMSS法的建立
1.1 能量有限元法和频响函数
能量有限元法的核心是以能量密度为基本变量,描述系统内部的能量分布。下面以一维结构为例进行推导。
处于稳态振动的一维结构中,能量由传播方向相反的2列行波(分别记为左行波和右行波)进行传递。在左行波中,任取一微元体,存在如图1所示的能量平衡关系,该能量平衡关系的表达式为[21]
(1)

由于系统处于稳态振动,所以一个周期内的平均能量密度为常数,即∂〈e-〉/∂t=0,其中符号〈·〉代表对变量在一个周期内进行时间平均。对式(1)在一个振动周期内进行时间平均,得到
(2)
同理,在右行波中也存在类似的能量平衡关系,如图2所示。由于右行波和左行波的能量强度方向相反,所以,右行波中的能量平衡关系为

图1 左行波能量平衡关系示意图Fig.1 Sketch of energy balance relationship in left-traveling wave

图2 右行波能量平衡关系示意图Fig.2 Sketch of energy balance relationship in right-traveling wave
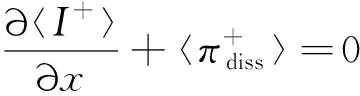
(3)
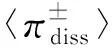
(4)
式中:η为结构阻尼比;ω为振动的圆频率。
另外,在每一列行波中,能量强度正比于能量密度[11],即
〈I±〉=cg〈e±〉
(5)
式中:cg为能量传播的速度,即群速度。
将式(4)和式(5)代入式(2)和式(3)可得
(6)
(7)
将左行波和右行波的能量密度进行叠加,可以得到结构各点的能量密度
〈e〉=〈e+〉+〈e-〉
(8)
由于左行波和右行波的能量强度方向相反,所以结构各点指向x正方向的净能量强度为
〈I〉=〈I+〉-〈I-〉
(9)
需要说明的是,式(8)和式(9)忽略了左行波和右行波之间的干涉作用,如果考虑干涉作用的影响,会导致能量密度和能量强度的分布出现空间谐波分量,此时需要对能量密度和能量强度在一个波长内进行空间平均,消除空间谐波分量,式(8)和式(9)才能适用[12-13]。
根据式(8)和式(9),用式(7)减式(6)可得
(10)

用式(3)减式(2),并结合式(4)和式(10),可得能量密度控制方程为
(11)
对式(11)可以采用有限元方法进行离散求解。采用伽辽金法,根据格林第二公式,可得每个单元内的能量有限元方程为
Κeee=Qe
(12)
式中:Κe为单元系数矩阵;ee为单元节点能量密度向量;Qe为进入单元的能量强度向量。
(13)

(14)
式中:Φ为单元形函数矩阵。
将各单元的能量有限元方程进行组装,可以得到结构的总体能量有限元方程,然后进行求解,得到结构各点的能量密度。其中,单元向量Qe组装成的总体向量Q的表达式为
Q=[0,…,0,P,0,…,0]T
(15)
式中:P为激励点处的输入功率。
输入功率P的计算可以采用阻抗法[11,17-20],即
(16)
式中:Frms为激励力的均方根值;Z为输入阻抗。在高频分析中,常用无限大结构的阻抗来近似有限大结构的阻抗[17-18],这样得到的输入功率并不是每一个激励频率下精确的输入功率,而是输入功率在每一个频段内的平均值。
在稳态振动下,经过时间平均和空间平均后,动能密度等于势能密度[12-13]。因此,通过能量有限元法获得结构各点的能量密度后,可认为动能密度是能量密度的1/2,所以可根据式(17)求得结构各点的速度均方根值
(17)
式中:ρ为密度;S为截面面积。进而可以得到各响应点与激励点之间的速度频响函数为
Hv=vrms/Frms
(18)
需要说明的是,式(18)所得速度频响函数Hv并不是精确的频响函数,而是频响函数在每一个频段内的平均值。这是因为能量有限元法的推导过程中进行了时间平均、空间平均,而且计算输入功率时采用了无限大结构的阻抗,所以能量有限元法的解并不是精确解,而是具有统计意义的结果,这一点与统计能量法类似。这种解在低频段会产生较大误差,但随着分析频率的升高,误差会逐渐减小。同时,进行频段平均等统计处理,需要保证频段内有足够多的模态数,才能具有足够的精度。对于统计能量法,要求一个频段内至少有5阶模态,对于能量有限元法,目前还没有确定的判据,但一般来说模态数越多精度越好。另外,在高频分析中,精确地分析每一个频率点处结构的响应会消耗大量的计算资源,而采用频段平均等统计思想,既可以提高计算效率,又可以在初步设计阶段较为准确地预示结构的高频响应[1],因此统计能量法和能量有限元法在高频振动响应分析中获得了广泛的应用。
1.2 虚拟模态综合法和瞬态响应分析
虚拟模态综合法的基本思想是通过已知的频响函数频段平均值,获得虚拟模态振型系数,来构造虚拟模态综合系统。
在小阻尼假设下,结构上i点和j点之间在频率ω处的速度频响函数的幅值可以按照模态叠加的形式表示为
(19)
式中:pm为第m阶模态频率;ζm=η/2为第m阶模态阻尼比;Ψim和Ψjm分别为第m阶模态振型向量的第i个和第j个元素;n为分析频带内的模态数。
在每个频段内取足够多的频率点,通过梯形积分,可以得到|Hij|在每个频段内的平均值为
(20)
式中:Δω为频段的带宽;s为该频段内频率点的个数。
式(20)可以写成矩阵的形式,即
BΨij=Hij
(21)
式中:Hij为速度频响函数频段平均值向量,可由能量有限元法获得;Ψij为虚拟模态振型系数向量,是各阶虚拟模态振型向量中与响应点和激励点对应的元素的乘积,即

(22)
由于频段数一般远小于模态数,所以矩阵B并不是方阵,则需要通过求矩阵B的广义逆矩阵的方式来求解式(21),得到

(23)
需要说明的是,Ψij不是结构精确的模态振型系数,而是虚拟模态振型系数。这是因为,在高频分析中结构模态密集,要精确计算结构的各阶模态参数变得困难,但可以计算结构的模态密度,进而得到结构在每个频段内的模态数,然后认为所有模态在每个频段内是均布的,从而得到各阶虚拟模态固有频率。Ψij正是这些虚拟模态的振型系数。虽然虚拟模态不是结构真实的模态,但能够确保虚拟模态综合系统的频响函数与结构精确的频响函数相比具有相同的频段平均值。因为虚拟模态综合法采用了这种频段平均的思想,所以只有在模态密集的高频段才能保证足够的精度。
获得虚拟模态振型系数Ψij后,便可以通过模态叠加法得到结构上任意一点i在k个激励下的位移时域响应为
(24)
式中:Rmj为第m阶模态力等于Qj(t)时第m阶模态位移的时域响应。
(25)
式中:Qj(t)为施加在j点的激励力的时间历程。
Rmj可以通过Duhamel积分进行计算,即

(26)
式中:h(·)为第m阶模态的位移脉冲响应函数。
通过类似式(24)~式(26)的方法,还可以得到结构各点的速度和加速度响应。
1.3 EFEM-VMSS法
能量有限元法可以进行高频稳态分析,得到结构频响函数的频段平均值,但无法进行瞬态响应分析。而虚拟模态综合法则能根据频响函数的频段平均值,进行瞬态响应分析。因此本文提出将能量有限元法稳态分析的输出结果,作为虚拟模态综合法的输入,从而完成高频冲击响应分析。如图3所示,为EFEM-VMSS法的分析流程。

图3 EFEM-VMSS法分析流程Fig.3 Flow chart of EFEM-VMSS
2 算例验证
为了验证本文建立的EFEM-VSMM法的正确性,并说明该方法的优点,下面以一个两端简支梁模型为研究对象,进行冲击响应分析,并与传统FEM和SEA-VSMM法的结果进行对比。简支梁模型如图4所示,梁长度l=4 m,密度ρ=2 700 kg/m3, 弹性模量E=71 GPa,结构阻尼比η=0.02,截面面积S=4×10-4m2,截面惯性矩Ib=1.33×10-10m4。图4中b1、b2和b3为3个响应点,到梁左端的距离分别为3l/8、l/4和l/8,a1和a2为2个激励点,到梁左端的距离分别为l/2和3l/4。
分析频带为891~14 130 Hz。工程中常按照倍频程、1/3倍频程或恒定带宽将分析频带划分为若干频段,本文按照表1将分析频带划分为12个1/3倍频程。虽然第1个频段内的模态数最少,为7个,但所有频段均满足统计能量法中一个频段内至少5阶模态的要求。
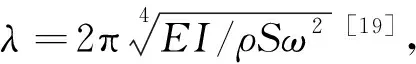

图4 简支梁示意图Fig.4 Sketch of a pinned-pinned beam
表1 1/3倍频程的中心频率和带宽
Table 1 Center frequencies and bandwidths of one-thirdoctave bands

频段号中心频率/Hz带宽/Hz11 000891~1 12221 2501 122~1 41331 6001 413~1 77842 0001 778~2 23952 5002 239~2 81863 1502 818~3 54874 0003 548~4 46785 0004 467~5 62396 3005 623~7 079108 0007 079~8 9131110 0008 913~11 2201212 50011 220~14 130
2.1 稳态分析结果

图5所示为激励频率f=10 kHz时梁上各点的横向振动速度均方根值。从图5中可以看出,SEA只能得到结构平均的速度均方根值,不能反映速度均方根值在结构内部的空间分布。
由于EFEM的推导过程中采用了局部空间平均,使得EFEM的结果并不表征某一点的速度均方根值,而是表征该点附近一个波长内平均的速度均方根值。因此,从图5中可以看出,EFEM的结果相当于FEM的结果在一个波长内进行了空间平均,消除了其空间谐波分量,但可以表征速度均方根值在空间的总体变化趋势。也正是因为EFEM只需要计算速度均方根值的总体变化趋势,不需要计算空间谐波分量,所以EFEM模型所需的单元数量很少。
图6和图7所示为分析频带内各响应点与激励点a1之间的速度频响函数(FRF)。其中图6为FEM和EFEM的结果对比,图7为SEA和EFEM的结果对比。从图6中可以看到,EFEM所得速度频响函数与FEM所得速度频响函数在每一个频段内的平均值吻合良好,对于不同位置的响应点,EFEM的结果都可以表征FEM的结果在频域的总体变化趋势。需要说明的是,正如1.1节中所述,EFEM的结果是时间、空间和频域上的统计结果,其求解精度随着频率增大而提高,因此,如图6所示,除个别频段外,总体上EFEM结果与FEM结果频段平均值之间的误差也随频率增大而减小。从图7中EFEM的结果可以看出,随着响应点与激励点之间的距离逐渐增大,速度频响函数逐渐减小,而SEA无法反映速度频响函数在结构内部的空间变化。

图5 速度均方根值分布Fig.5 Distribution of RMS of velocity
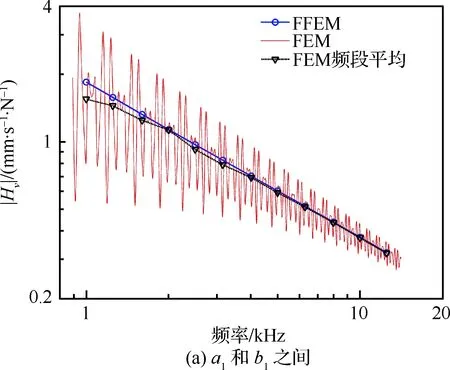

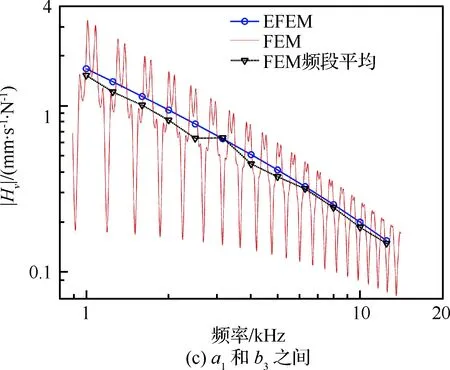
图6 EFEM和FEM所得的速度频响函数Fig.6 Mobility FRF obtained by EFEM and FEM

图7 EFEM和SEA所得的速度频响函数Fig.7 Mobility FRF obtained by EFEM and SEA
2.2 冲击响应分析
本节利用2.1节中稳态分析的结果和虚拟模态综合法,进行冲击响应分析,在本节的分析中,仅在激励点a1处施加如图8所示的三角脉冲激励。对于冲击响应分析的结果,采用加速度冲击响应谱(SRS)进行表达,加速度冲击响应谱的计算采用的是递归数字滤波法[23]。
图9和图10所示为分析频带内各响应点频段平均的加速度冲击响应谱。其中图9对比了FEM和EFEM-VMSS法的结果,图10对比了SEA-VMSS法和EFEM-VMSS法的结果。从图9中可以看出,通过EFEM-VMSS法得到的各响应点的加速度冲击响应谱与FEM的结果吻合良好,从而说明了本文建立的EFEM-VMSS法的正确性。需要说明的是,由于EFEM-VMSS法是在EFEM所得频响函数基础上进行冲击响应分析的,所以EFEM所得频响函数的精度总体上决定着EFEM-VMSS法所得冲击响应谱的精度,这一点结合图6和图9即可以看出。例如,8 kHz附近,图6(a)和图6(b)中EFEM和FEM所得的频响函数频段平均值误差很小,所以图9(a)和图9(b)中2种方法所得冲击响应谱峰值吻合良好。而图6(c)中EFEM所得的频响函数较大,从而导致图9(c)中EFEM-VMSS法所得的冲击响应谱峰值较大。

图8 三角脉冲Fig.8 Triangular pulse

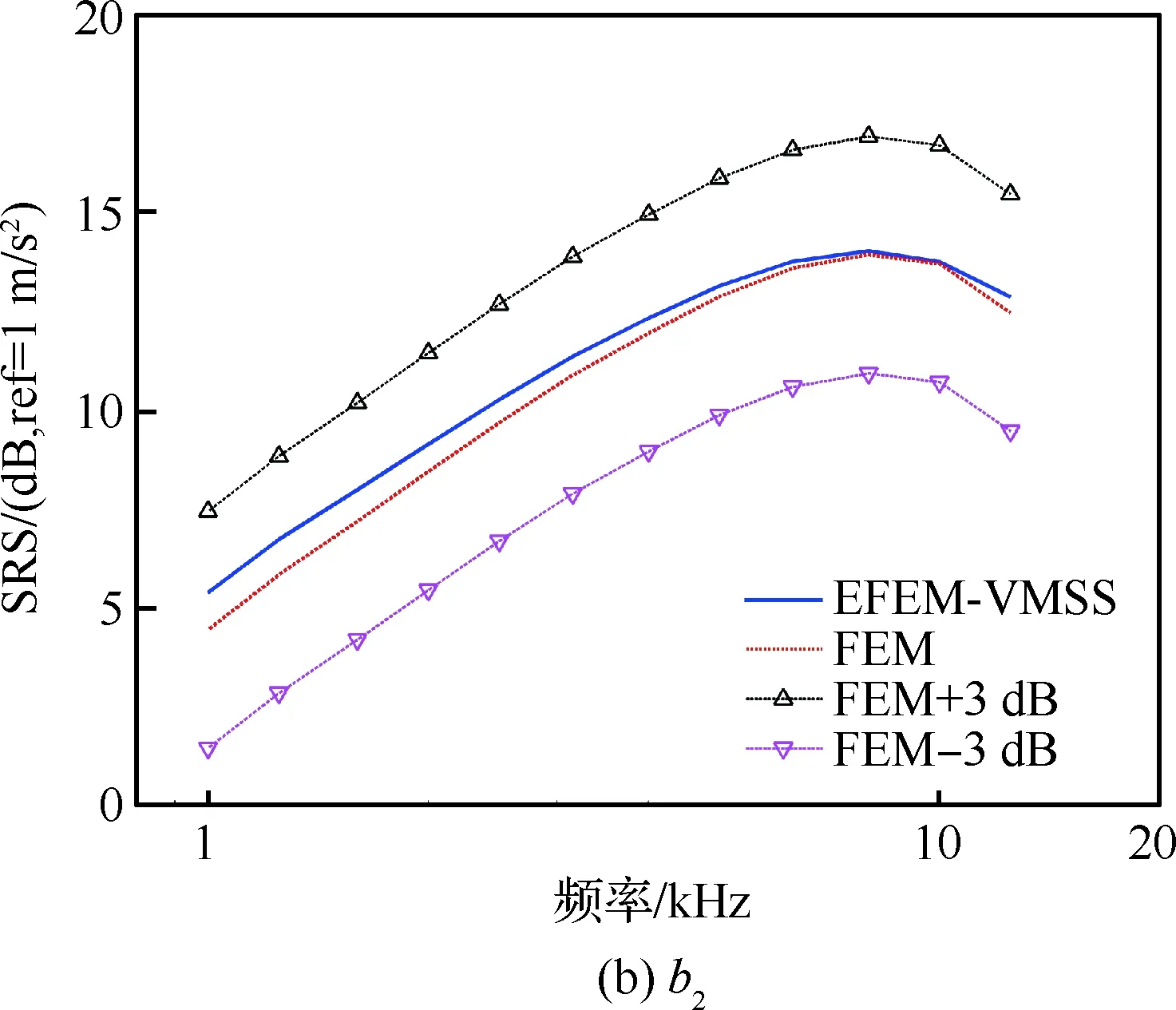

图9 EFEM-VMSS法和FEM所得冲击响应谱Fig.9 SRS obtained by EFEM-VMSS and FEM
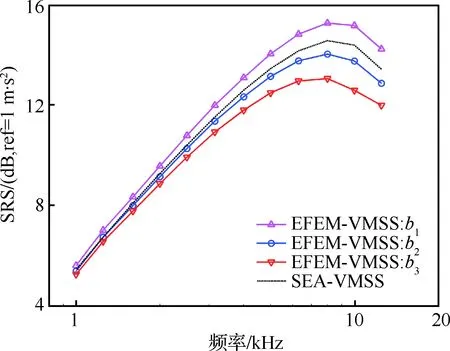
图10 EFEM-VMSS法和SEA-VMSS法 所得冲击响应谱Fig.10 SRS obtained by EFEM-VMSS and SEA-VMSS
从图10中EFEM-VMSS法的结果可以看出随着响应点与激励点之间的距离逐渐增大,加速度冲击响应谱逐渐减小,而SEA-VMSS法无法反映结构内部各响应点冲击响应谱的分布。
2.3 激励位置的影响
改变激励位置,仅在激励点a2处施加如图8所示的三角脉冲激励,通过EFEM-VMSS法进行冲击响应分析,并与激励位置为点a1时的结果进行对比,如图11所示。可以看出,随着激励点位置向右平移,即各响应点与激励点之间的距离均增大,导致各响应点的加速度冲击响应谱均减小。这表明EFEM-VMSS法可以分析不同激励位置下结构内部各点的冲击响应。而SEA-VMSS法受制于SEA理论,不能考虑激励点位置在结构内部的变化,在一个子系统内部不同位置进行激励,SEA-VMSS法所得结果是不变的。

图11 不同激励位置下EFEM-VMSS法所得冲击响应谱Fig.11 SRS obtained by EFEM-VMSS at different exciting positions
3 结 论
1) 详细推导了能量有限元法和虚拟模态综合法的基本方程及其求解过程,通过将能量有限元法和虚拟模态综合法相结合,提出了结构高频冲击响应分析的EFEM-VMSS法。通过算例分析,将EFEM-VMSS法的分析结果与FEM、SEA-VMSS法的结果进行了对比,验证了本文方法能够分析结构在高频冲击载荷作用下的瞬态响应。
2) 与FEM相比,EFEM-VMSS法具有模型简单、求解速度快的优点。与SEA-VMSS法相比,EFEM-VMSS法能够分析结构内部各点的冲击响应,而且能够考虑冲击载荷的作用位置。因此,本文提出的EFEM-VMSS法在高频冲击响应分析方面具有更好的适用性。

