基于分式析因设计的燕尾榫节点抗弯性能研究
杨 娜,钟 凯,秦术杰
(北京交通大学土木建筑工程学院,北京 100044)
0 引 言
中国传统木结构建筑中除椽子、望板这类屋面木基层构件外,其余几乎全部是通过榫卯形式连接在一起[1]。作为整体结构中起到拉结联系作用的榫卯节点,其力学特性影响并决定着整体结构的力学性能。
近几十年来学者们通过试验研究、有限元模拟和理论分析等方法对榫卯节点力学性能进行了大量研究。隋等[2]、陈庆军等[3]和淳庆等[4]通过对典型榫卯节点的低周反复荷载试验,研究了木构榫卯的转动特性和刚度退化规律,并给出了不同类型榫卯节点的恢复力曲线。文献[5],[6]通过改变某一特定参数,利用模型试验研究了不同因素对榫卯节点力学特性的影响。文献[7],[8]通过建立有限元模型,得到了榫卯节点的转动刚度,并对古木结构进行了静力分析。文献[9],[10]通过结合模型试验和有限元分析的方法对日本常见带木楔的直榫节点进行了研究,利用3D有限元模型与试验对比验证,分析了不同尺寸及形状的木楔对榫卯节点初始刚度及抗推压性能产生的影响。陈春超等[11-12]和谢启芳等[13-14]基于榫卯节点受力机理的分析,通过理论推导的方式得到了典型榫卯节点的弯矩-转角理论计算公式。以上研究揭示了榫卯节点的工作机制,也得到了节点的弯矩-转角关系等力学曲线,但仍存在一定的局限性:试验研究和有限元模拟往往只能得到特定条件下节点的力学性能指标;理论推导虽然能给出节点弯矩-转角曲线计算公式,但得到的理论公式通常过于复杂,掩盖了基本参数的影响规律且不利于实际工程应用。目前,对于考虑不同因素对榫卯节点力学性能影响的研究相对较少,特别是多因素相互作用的定量分析,且很少提出能够应用于实际的节点简化模型。
基于此,本文结合有限元模拟和分式析因设计方法,定量地研究弯矩作用下不同因素对燕尾榫节点抗弯性能的影响程度,给出节点初始转动刚度和极限弯矩的回归模型,并在此基础上提出可用于整体结构分析的燕尾榫节点弯矩-转角计算公式,为榫卯节点的抗弯性能研究提供一种新的思路和参考依据。
1 燕尾榫节点有限元模拟
数值模拟能够较为方便且高效地进行参数分析,为了利用有限元模拟进行分式析因设计,采用有限元分析软件ANSYS进行燕尾榫节点数值模拟研究,并利用文献[15]中的试验结果验证有限元建模方法的有效性。
1.1 燕尾榫节点有限元模型
燕尾榫节点是由燕尾形榫头和卯口组成的特殊节点,榫头的端部宽,根部窄,形成一种相互咬合的组合方式,如图1所示。选取文献[15]中的节点模型试验,用ANSYS软件建模,进行单调加载分析。梁、柱构件采用具有大变形等非线性能力的三维实体单元Solid185,榫卯连接处榫头插入卯口中,通过挤压、摩擦进行力的传递。为了模拟这种特性,在有限元模型中,榫头表面采用目标单元Target170,卯口表面采用接触单元Contact173,这2种单元可形成柔体-柔体的面面接触对,接触面之间的摩擦因数取0.4[16]。


木材为正交各向异性材料,根据文献[15]的材性结果给出樟子松的9个独立弹性常量,见表1,其密度文献[15]中没有给出,参考《木结构设计手册》[17]中樟子松的统计结果取为0.37 g·cm-3。
塑性计算时将木材近似看作理想弹塑性材料,并采用Hill型屈服准则[18]模拟木材的塑性屈服,木材塑性阶段的参数见表2,其中剪切屈服强度取值同样参考《木结构设计手册》[17]中樟子松的统计结果。

表1 樟子松相关力学参数Tab.1 Mechanical Parameters of Pinus Sylvestris Var
注:EL,ER,ET分别为顺纹、径向和弦向方向弹性模量;μLR,μLT,μRT分别为径切面、弦切面和横切面泊松比;GLR,GLT,GRT分别为径切面、弦切面和横切面剪切模量。

表2 樟子松塑性阶段参数Tab.2 Parameters of Pinus Sylvestris Var at Plastic Stage MPa
将柱的上下端面进行固接,并在梁自由端上边界线处施加单调的位移荷载,对模型中三维部件采用扫掠网格划分技术,且在榫卯连接处进行网格细分,如图2所示。


1.2 有限元模拟结果对比
提取有限元计算结果中每一个荷载子步下梁端的合力以及榫头转动的角度θ,将梁端合力与梁长相乘得到榫头所受弯矩M,由此作出榫卯节点的弯矩-转角曲线,并与试验曲线进行对比,结果如图3所示。由图3可知,数值模拟得到的弯矩-转角曲线与试验给出的曲线基本吻合,结果表明,数值模拟较为准确地反映了燕尾榫受弯的真实受力状态,从而验证了数值模拟方法的有效性。


2 燕尾榫节点分式析因试验
析因设计是一种同时研究多个因素及其交互作用对系统影响的方法,它广泛应用于涉及多因素的试验,并被认为是最为有效的方法之一[19]。如果考虑所有因素的影响将导致试验次数剧烈增加,假设试验有k个影响因素,每个因素有2个水平,则完全析因设计的试验数为2k个,当k达到较大值时,进行试验将需要耗费大量资源甚至难以实现。此时分式析因设计是一种很有效的方法,它能够用较少的试验从众多的输入变量中筛选出影响系统的关键因素和重要的交互因素。
本文以数值模拟的方法代替真实试验进行分式析因设计,以研究不同因素对燕尾榫节点抗弯性能的影响程度,并给出回归模型。
2.1 分式析因数值模拟试验
总结已有研究成果[11,13],选取榫高A、榫长B、榫头宽C、摩擦因数D、横纹抗压强度E、横纹弹性模量F以及收乍角度G作为分式析因数值模拟试验的7个因素,每个因素取2个水平,影响因素及其水平选取如表3所示,图4为燕尾榫尺寸标注示意图。

表3 因素和水平Tab.3 Factors and Levels
注:以收乍角度的正切值表示G的大小。


因素水平的选取至关重要,其选取原则是与实际情况相符并能给出较大适用范围。对于榫头尺寸因素(表3中的前3种因素及收乍角度)来说,根据《工程做法则例》选取能包含大多数建筑的尺寸范围,据此给出各尺寸的相关取值。对于木材的横纹抗压强度而言,根据《木结构设计手册》附录四的试验结果,选取能够包含大多数木材横纹抗压强度值的范围。对于木材的横纹弹性模量及摩擦因数则参考《机械设计手册》,分别取所给范围的最大值和最小值。
选用的分式析因试验方案见表4,共建立了32个数值计算模型。提取每个模型的弯矩-转角曲线,并确定后续进行统计分析所需的样本值。
2.2 燕尾榫节点抗弯性能影响因素显著性分析
选取初始转动刚度和极限弯矩承载力作为分式析因试验的评价指标,这2个指标是后续研究的基础,其中初始刚度为曲线的初始斜率值,极限弯矩承载力为曲线的峰值。对32组计算样本值进行统计分析,在显著性水平α=0.05下,利用方差分析针对不同指标筛选出相应的显著因素,剔除不显著因素。将各显著因素的效应值(单因素的效应值为因素水平改变时所产生响应的变化,交互作用效应值为一个因素的水平间的响应差随其他因素水平不同产生的响应变化)列于表5,其中贡献率是相应因素效应的绝对值占所有因素效应绝对值总和的百分比。需要说明的是,二阶交互效应的总项数应该为21个,表5中只给出了14项,其余未给出交互项说明其对2个指标的影响均不显著。
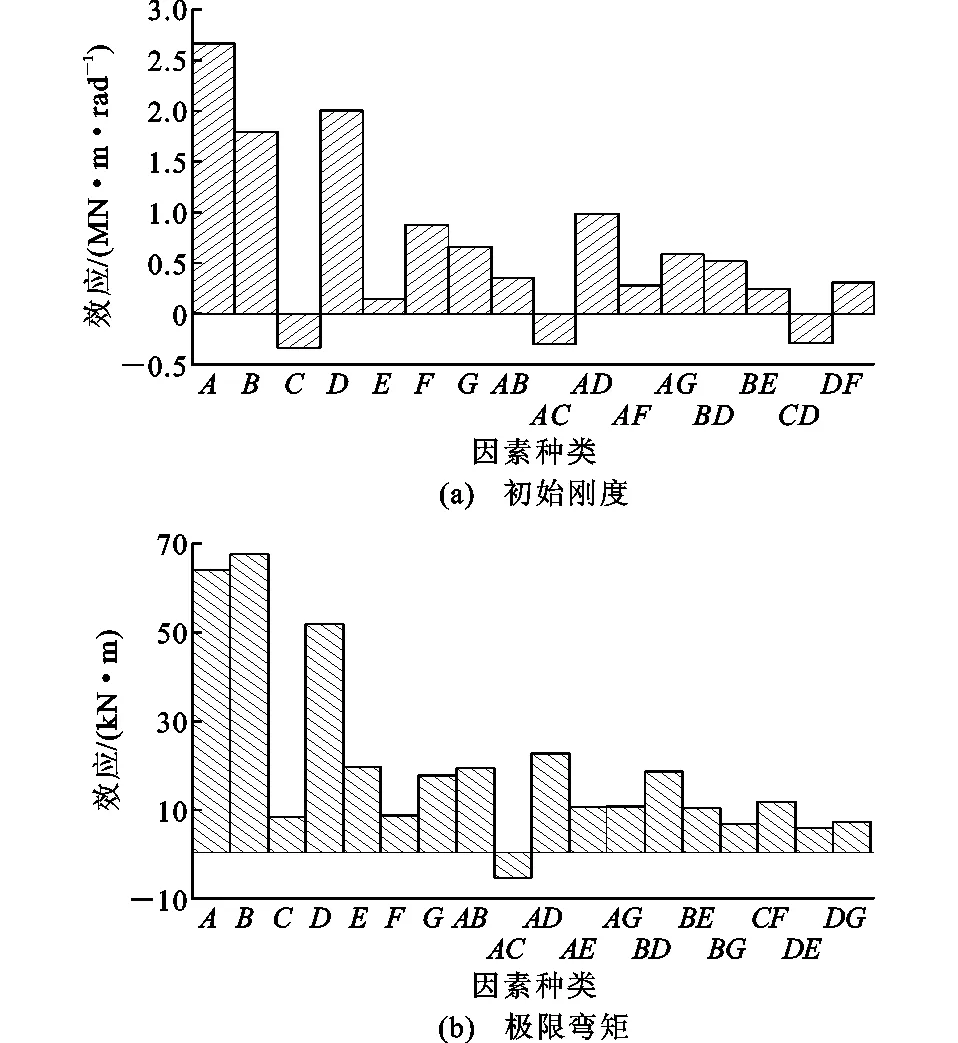
为了更直观地比较不同因素对各指标的影响程度,做出不同指标下各因素效应的柱状图,如图5所示。效应值为正(负)表示相应指标随该因素的增大而增大(减小),而效应值的绝对值则反映了因素对评价指标的影响程度。

表4 分式析因数值模拟试验方案Tab.4 Schemes of Fractional Factorial Numerical Simulation Test
由表5和图5可知,对于燕尾榫节点的初始刚度,A(榫高)、D(摩擦因数)和B(榫长)这3个因素的贡献率都在10%以上,且效应总和占所有显著因素效应总和的半数以上,说明这3个因素的影响程度最为显著。值得一提的是,在所有主效应因素中,只有C(榫头宽)对初始刚度的影响是负增长,且所有包含C(榫头宽)的交互作用效应都是负值,这说明C(榫头宽)过大可能会在一定程度上降低燕尾榫节点的初始转动刚度。对于燕尾榫节点的极限弯矩,B(榫长)、A(榫高)和D(摩擦因数)这3个因素依然占有决定性作用,且几乎所有显著性因素的影响都是正向的,这与转动刚度的结果是略有差别的。

表5 不同因素贡献率Tab.5 Contribution Rates of Different Factors
注:“-”表示此因素对相应指标影响不显著;双字母表示各因素的交互作用。

以上分析结果表明,榫高、榫长以及摩擦因数的改变会对燕尾榫节点的力学性能产生较大影响,在对节点的加固维修中应重点考虑这3个因素对节点性能的影响。同时,在燕尾榫节点数值模拟过程中,对榫头尺寸以及摩擦因数的准确把握程度会在一定范围内影响最终结果的准确性。
2.3 统计回归模型及其验证
对32组样本数据进行统计回归,可得榫卯节点初始转动刚度关于所选7个因素的回归模型Kr为
Kr=3 247-10.72A-11.27B+15.18C-
7 795D-100.1E-1.328F-29 733G+
0.030 89AB-0.023 26AC+15.41AD+
0.003 61AF+87.7AG+36.10BD+0.906BE-
18.06CD+3.199DF
(1)
同理可得极限弯矩的回归模型Mr为
Mr=260.0-0.321A-1.132B-0.119C-
334.2D-8.29E-0.0610F-1 319G+
0.001 663AB-0.000 433AC+0.351 0AD+
0.008 59AE+1.576AG+1.284BD+0.037 28BE+
4.40BG+0.000 604CF+3.74DE+847DG
(2)
为了验证回归模型的准确性,另选取2种规格的燕尾榫节点X1和X2(表6)进行建模分析,将模拟结果的样本值与上述的回归模型拟合值进行对比,如表7所示。可以看出,极限弯矩的拟合值与样本值相差不大,说明其回归模型的预测结果具有较高的可靠度,而初始刚度的拟合值和样本值相差较大,但也控制在30%以内,当缺乏试验数据时,依据回归模型计算的预测结果具有一定的参考价值。

表6 节点模型参数Tab.6 Model Parameters of Joint

表7 结果对比Tab.7 Comparison of Results
3 燕尾榫节点弯矩-转角计算模型
榫卯连接的古木结构是一半刚性连接的结构,对这样的结构进行整体力学性能分析的关键在于选取合理的榫卯节点简化模型。文献[20]指出,古木结构榫卯连接的半刚性研究多采用三折线模型和三参数幂函数模型[21],其中又以三参数幂函数模型较为理想,被广泛应用。三参数幂函数模型可写为
(3)
式中:Rk为曲线初始刚度;n为形状系数;θ为参考塑性转角;θu为极限塑性转角,θu=Mu/Rk,Mu为节点抗弯极限弯矩。
从模型的计算公式可知,要得到最终的模型曲线需要确定3个关键参数,即初始刚度Rk、形状系数n以及极限弯矩Mu。利用公式(1),(2)可确定初始刚度以及极限弯矩,根据文献[20]确定形状参数n的取值为3。
以表6中的2种节点模型为研究对象,对比数值模拟结果和三参数幂函数模型结果,如图6所示。


由图6可知,两者的弯矩-转角曲线基本吻合,说明基于回归模型得到的三参数幂函数模型在考虑榫卯节点尺寸、木材材性以及摩擦因数等因素影响下能够很好地描述榫卯节点的抗弯性能。在进行整体结构力学性能分析时,可直接利用上述方法进行节点抗弯性能的计算,方便实际工程应用。
4 结 语
(1)本文采用的结合有限元模拟和分式析因设计技术的方法经过验证是行之有效的,定量分析了榫高、榫长、榫头宽、摩擦因数、横纹抗压强度、横纹弹性模量以及收乍角度这7个因素对燕尾榫节点初始转动刚度和极限弯矩承载力的影响程度,并提出了相应的回归模型。
(2)所选取的7个因素对燕尾榫节点的初始刚度和极限弯矩承载力的影响程度不同,其中榫高、榫长和摩擦因数对2个性能指标的影响最为显著,建议在维修加固中重点考察这3个因素的损伤状态。
(3)几乎所有因素与燕尾榫节点的抗弯性能都是正相关的,只有榫头宽对节点初始刚度的影响是负增长,即榫头宽的增大会在一定程度上减小节点刚度。
(4)通过统计回归提出了燕尾榫节点初始刚度和极限弯矩的回归模型,并给出了结合回归模型的三参数幂函数模型,对比结果显示这一简化模型可概括性地描述燕尾榫节点的半刚性特性,在保证一定可靠性的基础上计算简单,便于应用,可为整体结构力学分析提供参考依据。

