带否定算子的兰贝克演算研究*
林哲
中山大学哲学系 中山大学逻辑与认知研究所linzhe8@mail.sysu.edu.cn
梁飞†
山东大学哲学与社会发展学院philoliangfei@gmail.com
1 引言
J.Lambek于1958年为自然语言计算引入了一个句法演算系统。([7])现在这个系统被统称为兰贝克演算。在过去几十年间,兰贝克演算在语言逻辑领域受到了广泛的重视,并且发展出许多重要的衍生和扩张。W.Buszkowski于1995年在论文[1]中引入带否定算子的兰贝克演算作为学习范畴语法的核心类型逻辑。Buszkowski在其文章中提出,作为学习范畴语法的核心类型逻辑,其否定规则只需要满足:
·置换性:假如类型A推出类型B,那么有¬B推出¬A,和
·双重否定率:对任何类型A:¬¬A=A。
有别于这种观点,在兰贝克演算的扩张研究中,构造性否定被广泛关注即类型的否定被定义为¬A:=A⊥。由于兰贝克演算一般不具有交换律,因此会产生两个否定。对这样的扩张的研究可以在文献[3,6]中找到详细的阐述。然而构造性否定会带来另外一个问题,即兰贝克矛盾律α·¬α=⊥在逻辑中会变成有效。这条性质缺乏语言逻辑研究的动机,并且还会破坏一些范畴语法系统所需要的性质,因此Buszkowski提出的兰贝克否定扩张更适合作为范畴语法的类型逻辑来研究。但是这种兰贝克演算其判定性是未知的,并且缺乏优秀的根岑演算系统。这会对基于这种类型逻辑范畴语法的进一步研究带来巨大的不便。
在本文我们选择了一种极为接近Buszkowski提出的否定,称为极小否定。极小否定满足置换性和一半的双重否定律:任何类型A推出类型¬¬A,并且在极小否定中对任何¬¬A类型都满足上述否定的两个性质。极小否定的概念最早是由A.Kolmogorov([5])提出,再由I.Johansson([4])的研究发展得到。Johansson提出了一个极小逻辑,这一极小逻辑是由直觉主义逻辑删除Duns Scotus公理A→(¬A→B)得到。根据M.Dunn在其“Dunn’s Kite of Negations”([2])的研究,极小否定是一种否定,满足如下性质:A⊢¬B当且仅当B⊢¬A。在本文中,我们研究了兰贝克演算的极小否定扩张,并且证明了这种扩张具有判定性,同时提出了一个满足切割消除和子公式性质的兰贝克演算极小否定扩张的根岑演算系统。最后我们通过构造一个翻译,将兰贝克演算的德摩根扩张嵌入到兰贝克的弱极小否定扩张,从而证明兰贝克演算的德摩根扩张的判定性。
2 极小否定兰贝克演算及其代数模型
令ALM的语言递归定义为:

ALM的代数系统由公理

和以下的规则组成:

如果把ALM的语言限制到不包含¬,⊥,⊤的公式,并且在系统中把公理规则(⊥)、(⊤)和(CT)去掉,那么得到的就是经典的兰贝克演算系统L。
定义1剩余半群(G,·,,/,≤)被定义为如下代数结构:
1.(G,≤)是一个偏序;
2.(G,·)是一个半群;
3.·,,/为G上的二元算子并且满足下面的剩余规则

在剩余半群的定义中,假如将(G,·)替换成群胚,即(·),得到的是剩余群胚。如果同时令·满足交换律,那么相应得到的是交换剩余半群和交换剩余群胚。
定义2极小否定剩余半群(G,·,,/,≤,⊥,⊤,¬)被定义为如下代数结构:
1.⊥,⊤分别为G中的极小和极大元;
2.(G,·,,/,≤)是一个剩余半群;
3.¬为G上的一元算子并且满足下面的极小否定规则:

定理1L对剩余半群是有效和完全的。
证明:L有效性证明是显然的,完全性证明使用林登保姆–塔斯基方法构造句法模型可证。证明思路大致如下。首先取一个剩余半群(M,·,≤)是一个剩余半群,其中M为公式集。然后我们选择M所有的下闭包子集的集合C(M),在C(M)上面定义三个算子×,,/如下:

显然代数(C(M),×,,/)就是一个剩余半群。在L系统上定义公式集为[A]:={B:⊢B⇒A},则[A]为一下闭包集。在所有的[A]组成的集合上如上定义×,,/,得到一个包含所有公式等价类的典范模型。因此可以很容易证明L相对这个模型是完全的。
下面定理2、定理4证明方法类似,只需要在选取剩余半群时选取了添加了对应算子¬,⋆及包含其性质的代数结构,其他证明步骤是相同的。
定理2ALM对极小否定剩余半群是有效和完全的。
定义3极小否定剩余半群群胚(G,·,,/,≤,⊥,⊤,⋆,→)被定义为如下代数结构:
1.(G,·,,/,≤,⊥,⊤,¬)为极小否定剩余半群,其中令¬a:=a→⊥;
2.(G,⋆,→,≤)为交换剩余群胚。
定理3任意极小否定剩余半群都能被扩张成一个极小否定剩余半群群胚。
证明:令G=(G,·,,/,≤,⊥,⊤,¬)为一个极小否定剩余半群。定义G二元算子⋆和→如下:

下面证明·和→满足如下三个条件:
1.a·b=b·a;
2.¬a=a→⊥;
3.a·b≤c当且仅当b≤a→c。
由定义可以简单得到条件1,条件2成立。下面证明条件3成立。假设c=⊤时,那么a·b≤c自然成立;同时a→c=⊤,因此b≤a→c。令a·b≤c。因为c̸=⊤,所以a·b=⊥。根据定义有a≤¬b,因此b≤¬a。又因为a→c=¬a,所以b≤a→c。反之,假设b≤a→c。因为c̸=⊤,所以a→c=¬a。因此b≤¬a。根据定义b·a=⊥,可得a·b=⊥,那么有a·b≤c。因此G是一个一个极小否定剩余半群群胚。
令系统ALM+的语言递归定义为:

令系统ALM+是由系统ALM去掉规则(CT)并添加公理A⋆B⇔B⋆A和如下规则得到:

定义¬A:=A→⊥,则规则(CT)在ALM+是可证的。证明如下:假设A⇒B→⊥。由LRes′2可得B⋆A⇒⊥。因为A⋆B⇒B⋆A,根据(Cut)A⋆B⇒⊥以及LRes′1可得B⇒A→⊥。
定理4ALM+对极小否定剩余半群群胚是有效和完全的。
定理5对于任何ALM简单序列A⇒B,ALM⊢A⇒B当且仅当ALM+⊢A⇒B。
证明:从左到右的方向显然可证。从右到左的方向,这里采用反证法的方式进行证明。假设ALM̸⊢A⇒B。那么根据定理2,存在一个极小否定剩余半群G使得G̸⊢A⇒B。根据定理3,G可扩张为一个极小否定剩余半群群胚G′使得G′̸⊢A⇒B。再根据定理4,可得ALM+̸⊢A⇒B。
3 根岑序列演算与判定性
本节将首先讨论ALM+的根岑系统LM+,同时将证明LM+是可判定的,在此基础上得到LM的判定性和根岑系统。LM+的公式定义与ALM+相同。LM+的公式结构是由公式通过结构算子(,)和(◦)生成。公式串列可以递归定义如下:

序列Γ⇒A是由公式结构Γ、公式A和符号⇒组成。任何一个公式结构Γ代表一个公式f(Γ)。f(Γ)可以递归定义如下:

符号Γ[−]代表一个公式结构中存在着一个位置−。符号Γ[∆]则代表在Γ[−]中的−位置中替代入公式结构∆。
LM+的根岑序列系统由公理
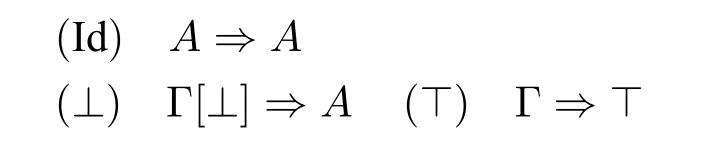
和以下的规则组成:
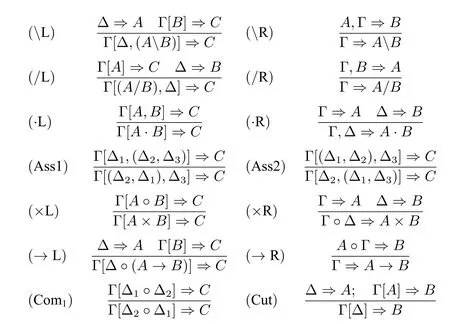
定理6(切割消除) 任何在LM+下可证的序列都存在一个LM+中不使用切割规则的证明。
证明:只需要证明假如(Cut)规则的两个前提都存在LM+下不使用(Cut)的证明,那么(Cut)规则的结构同样存在LM+下不使用(Cut)的证明。假设推导中的某一个(Cut)如下:
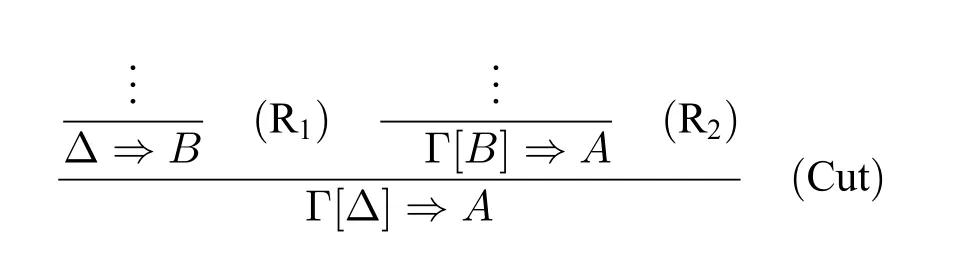
施归纳假设于(i)切割公式的复杂度,即切割公式中包含的连接词数量。在归纳假设(i)中我们再施归纳假设于(ii)(Cut)规则的度,即切割规则两个前提的证明总长度。
假设(Cut)规则的前提分别由规则R1和R2得到,下面分三种情况讨论:
1.至少R1或R2是公理;
2.R1或R2没有引入切割公式;
3.R1和R2同时引入切割公式。
1.假设R1或R2是公理。考虑下面的情况:
(a)如果∆=B,那么Γ[B]⇒A等于切割结论;
(b)如果⊥∈∆,⊥∈Γ或A=⊤,那么Γ[∆]⇒A也是公理;
(c)如果Γ=ε并且B=A,那么∆⇒B等于切割结论;
(d)如果B=⊤并且Γ[B]⇒A不是公理,那么对R1的和R2中包含⊤的前提使用切割规则,然后再使用R2,根据归纳假设(ii),结论成立;
(e)如果B=⊥并且∆⇒B不是公理,那么证明方法与情况(d)类似。
2.令R1或R2没有引入切割公式B。当R1或R2是(Com)或(Ass)时,证明是显然的。下面证明当R1是(→L)时结论成立。其他情况可用类似方法证明。假设(Cut)规则的子推导树如下:
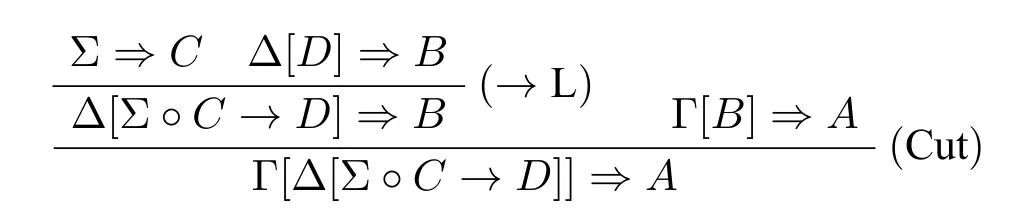
将上面的推导树改写成如下推导树
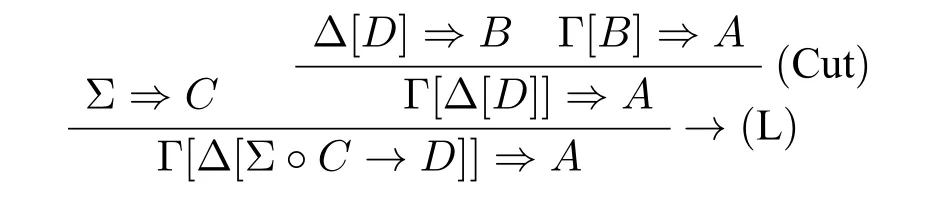
新的切割规则的度要小于旧切割规则的度,因此根据归纳假设(ii)结论得证。
3.R1和R2同时引入切割公式B。下面证明当B等于B1→B2时结论成立。其他情况可用类似方法证明。假设(Cut)规则的子推导树如下:

将上面的推导树改写成如下推导树:
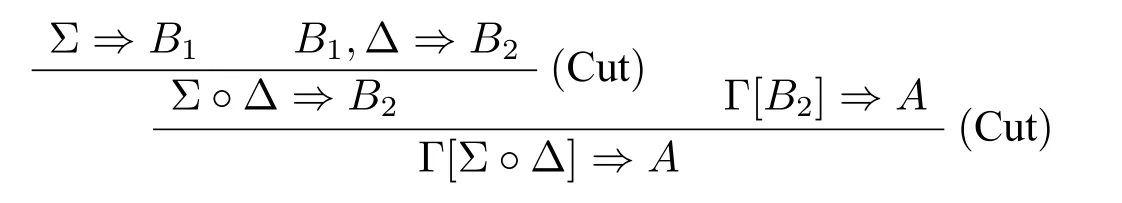
新的切割公式的复杂度要小于旧切割公式的复杂度,因此根据归纳假设,(i)结论得证。
推论1如果LM+⊢Γ⇒A,那么存在一个LM下Γ⇒A的证明,使得包含在证明中的公式均为序列Γ⇒A中出现的公式的子公式。
定理7LM+是可判定的。
证明:根据定理6,对任何序列Γ⇒A,如果其在LM+中可证,那么必然存在LM+中不使用切割规则的证明。那么以Γ⇒A为根节点向上遍历其在LM+中的推导树。根据推论1和LM+的规则可知,可以出现在推导树中节点的不重叠序列的个数是有穷的。并且在推导树中每一个分支上不会出现两个节点使得节点上的序列是相同的。因此可以得到该推导树的深度,即最长分支的长度是有穷的。同时根据LM+的规则可知该推导树是二叉树。已知对任意二叉树,假如其深度是有穷的,那么该二叉树的规模即节点总数是有穷的。因此以Γ⇒A为根节点向上遍历其在LM+中的推导树是有穷的。因为规则的个数是有穷的,遍历序列在LM+中的推导树这个过程是有穷的,因此LM+是可判定的。
定理8LM是可判定的。
证明:由定理5和定理6直接可得。
根据定理5与推论1可以得到LM+的根岑序列演算LM。LM由公理

和以下的规则组成:

定理9ALM⊢α⇒β当且仅当LM⊢α⇒β。
弱LM指由LM去除(Com)所得到的逻辑。由上面证明可以简单得到
定理10弱LM是可判定的。
在弱LM中可证α⇒β蕴含¬β⇒α,但不可证α⇒¬¬α。这里记弱LM为LM−
引理1如果LM−⊢Γ◦¬α⇒⊥,那么LM−⊢Γ⇒α。
由简单的施归纳于Γ◦¬α⇒⊥在LM−中的证明长度可证。注意◦在这里是非结合算子,如果◦是一可结合算子则该引理不成立。
引理2如果LM−⊢Γ⇒¬α,那么LM−⊢Γ◦α⇒⊥。
简单由由¬α的剩余性质可证明。
L的德摩根扩张是指在L上额外添加一个德摩根否定算子:即满足α⇒β蕴含¬β⇒α和α⇔¬¬α.L的德摩根扩张逻辑可以简单的由LM添加公理¬¬α⇒α得到。这里将L的德摩根扩张记为LDM。
定义一个从LDM公式到LM−公式的递归翻译k:
定义4
·k(p)=p;
·k(¬nα)=¬mα m=mod(n,2),并且α不是一个形为¬β的公式;
·k(α⋆β)=k(α)⋆k(β),其中⋆∈{·,/,}。
k可自然延展为从LDM公式结构到LM−公式结构的翻译。
引理3如果LDM⊢Γ⇒β,那么LM−⊢k(Γ)⇒k(β)。
对该引理的证明,只需要证明LDM中的公理和规则在LM−下都是可证的。由简单施归纳于LDM⊢Γ⇒β可证。上面两个引理保证了LDM否定规则的k翻译在LM−下是有效的。
定理11LDM是可判定的。

