YAU’S UNIFORMIZATION CONJECTURE FOR MANIFOLDS WITH NON-MAXIMAL VOLUME GROWTH∗
Binglong CHEN(陈兵龙)Xiping ZHU(朱熹平)
Department of Mathematics,Sun Yat-sen University,Guangzhou 510275,China
E-mail:mcscbl@mail.sysu.edu.cn;stszxp@mail.sysu.edu.cn
Abstract The well-known Yau’s uniformization conjecture states that any complete noncompact Kähler manifold with positive bisectional curvature is bi-holomorphic to the Euclidean space.The conjecture for the case of maximal volume growth has been recently con firmed by G.Liu in[23].In the first part,we will give a survey on the progress.In the second part,we will consider Yau’s conjecture for manifolds with non-maximal volume growth.We will show that the finiteness of the first Chern number is an essential condition to solve Yau’s conjecture by using algebraic embedding method.Moreover,we prove that,under bounded curvature conditions,is automatically finite provided that there exists a positive line bundle with finite Chern number.In particular,we obtain a partial answer to Yau’s uniformization conjecture on Kähler manifolds with minimal volume growth.
Key words uniformization conjecture;non-maximal volume growth;Chern number
1 Introduction
In Kähler geometry,there is a well-known uniformization conjecture due to Yau[38]:
Conjecture 1.1Let(Mn,g)be a complete noncompact Kähler manifold with positive bisectional curvature of complex dimension n.Then Mnis biholomorphic to Cn.
This conjecture was motivated,on the one hand,by the classical uniformization theorem for Riemann surfaces,and by a famous result in Riemannian geometry due to Gromoll-Meyer which says that a complete noncompact Riemannian manifold with positive sectional curvature is di ff eomorphic to the Euclidean space.This conjecture has aroused a great interest in mathematics since it was introduced,it stimulated a lot of researches during the past decades(see[4,5,14,17,23,26,29,34]or references therein).Although there already have been many accomplishments,even breakthroughs for maximal volume growth case,it is an embarrassing fact that presently we even do not know if a complete noncompact Kähler manifold with positive bisectional curvature is Stein or di ff eomorphic to the Euclidean space.
1.1 Main techniques
In principle,we have two approaches to solve Conjecture 1.1:
a)construct a complete flat Kähler metric on Mn,
b)directly construct a biholomorphic map from Mnto Cn.
For a),one may use geometric flows to deform the initial metric(e.g.Ricci flow),roughly speaking,we hope that the limit will provide a desired flat Kähler metric on Mn.Ricci flow is the following deformation equation on metrics:

For b),we need to construct holomorphic functions or holomorphic sections of some line bundles.A conservative way is first to embed Mnto CNor CPNas an affine or quasi-projective variety for some large N,this process is called compacti fication.In views of complex analysis,the key point for this process is to find a pluri-subharmonic functionthat the L2estimate for−equation of Hörmander[19]and Andreotti-Vesentini[1]could be applied.
The construction of the holomorphic map in b)depends on the geometry of the background manifold,in practical applications,one can combine a)and b),i.e.,deform the background geometry,and accomplish b)by using the geometric informations from a family of deformed metrics(see[4,14]).
Geometric construction from triangle comparison theorem usually only gives a Lipschitz continuous auxiliary function satisfying certain convexity conditions.To obtain a smooth one,one can use heat equation to deform it:

The point is that the Levi-form(on Kähler manifold)satis fies a parabolic Lichnerowicz equation:
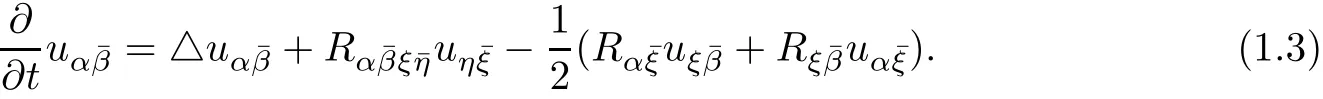
Under certain growth condition of the solution u,for instance,orif the bisectional curvature is nonnegative,i.e.,one can show thatis preserved by the heat equation(if it holds initially),moreover it becomes strictly positive for t>0,i.e.,unless the universal cover of the manifold splits isometrically as a nontrivial product M=N×L,see[32].Surely,the splitting can not happen if we assume the bisectional curvature or Ricci curvature is strictly positive.
So we have two kinds of deformations available,(1.1)and(1.2),one is for metics,the other is for functions.
In[12],Cheeger-Gromoll proved that a complete Riemannian manifold with nonnegative sectional curvature is di ff eomorphic to the normal bundle of a compact totally geodesic submanifold.The Kähler analogue was obtained in[13](Page 60-65):
Theorem 1.2(Cao-Chen-Zhu[13])Let M be a complete noncompact Kähler manifold with bounded and nonnegative holomorphic bisectional curvature.Then one of the following holds:
(i)M admits a Kähler metric with bounded and positive bisectional curvature;
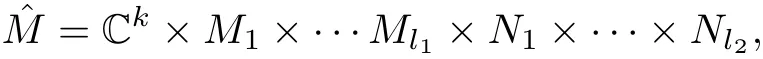
where k,l1,l2are nonnegative integers,Ckis the complex Euclidean space with flat metric,Mi,1 ≤ i≤ l1,are complete(compact or noncompact)Kähler manifolds with bounded and nonnegative bisectional curvature admitting a Kähler metric with bounded and positive bisectional curvature,Nj,1≤j≤l2,are irreducible compact Hermitian symmetric spaces of rank≥2 with the canonical metrics.
In the above theorem,the manifold(passing to the universal cover in case ii)is a metric product,not only a fiber bundle.The argument is a delicate maximum principle type argument,which was used by Gu[21]to give an alternative and transcendental proof of generalized Frankel conjecture due to Mok[28],see[13](Page 60-65)for details.This theorem reduces the study of the case of nonnegative bisectional curvature to the strictly positive one,if we assume the curvature is bounded.
Let us begin with a theorem of Mok-Siu-Yau[29]in 1981:
Theorem 1.3(Mok-Siu-Yau[29])Let M be a complete non-compact Kähler manifold of non-negative holomorphic bisectional curvature of complex dimension n≥2.Suppose there exist positive constants C1,C2such that for a fixed base point x0and some ǫ>0,
(i)Vol(B(x0,r))≥C1r2n,0≤r<+∞,
(ii)R(x)≤ C2/d(x0,x)2+ǫon M,
where Vol(B(x0,r))denotes the volume of the geodesic ball B(x0,r)centered at x0with radius r,R(x)denotes the scalar curvature and d(x0,x)denotes the geodesic distance between x0and x.Then,M is isometrically biholomorphic to Cnwith the flat metric.
The seminal idea to find a pluri-subharmonic function in Mok-Siu-Yau[29]is to solve the Poincare-Lelong equation:

The conditions(i)and(ii)guarantee a bounded solution u to the Poincare-Lelong equation(1.4).This bounded pluri-subharmonic function u must be constant by the virtue of Yau’s Liouville theorem,whence the manifold is actually flat.This result is called a gap theorem,which means that there is a gap on the order of the curvature decay on a nonnegatively curved manifold,more precisely,it is actually flat if the curvature decays faster than quadratic.
Except the curvature sign,the conditions in Mok-Siu-Yau’s theorem consist of two things:i)volume growth,ii)curvature decay.All the subsequent works trying to solve the uniformization conjecture assumed conditions of the above two types.We have to mention that,from the recent result of Liu[23],Yau’s conjecture is true if the manifold has nonnegative bisectional curvature and maximal volume growth.In previous works,under the maximal volume growth and bounded curvature conditions,Yau’s conjecture has been con firmed in Chen-Tang-Zhu[14](for complex dimension 2)and Chau-Tam[4](for all dimensions).However,not much is known when the volume growth is not maximal.In some sense,the maximal volume growth more or less forces the geometry of the manifold at in finity to approximate to that of the Euclidean space.In the non-maximal volume growth case,the geometry at in finity is complicated.
1.2 Geometry of bisectional curvature
In[17],we proved the following theorems on the volume growth and curvature decay of any complete Kähler manifold with positive bisectional curvature:
Theorem 1.4(Chen-Zhu[17])Let Mnbe a complex n-dimensional complete noncompact Kähler manifold with positive holomorphic bisectional curvature.Then the volume growth of M satis fies
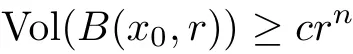
for all 1≤r<∞,where c is some positive constant depending on x0and the dimension n.
Theorem 1.5(Chen-Zhu[17]) Let Mnbe a complete noncompact Kähler manifold with positive holomorphic bisectional curvature.Then for any x0∈Mn,there exists a positive constant C such that
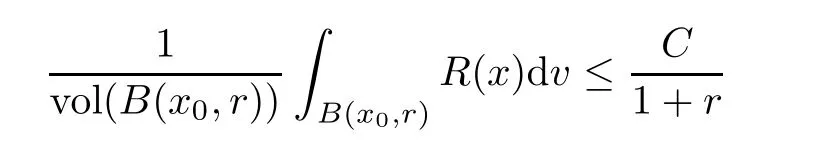
for all 0≤r<∞,where R(x)is the scalar curvature of Mn.
Roughly,it says that the volume of a geodesic ball of radius r grows at least as fast as rn,where 2n is the real dimension of the manifold,the average of the curvature decays at least linearly.It is surprising that these two results are sharp,in the sense that we do have a lot of examples satisfying these minimal volume growth and curvature decay conditions,e.g.Klembeck’s examples,Cao’s static Kähler-Ricci solitons with positive bisectional curvature,see[3].

Let P ∈ Mn,γ :[0,∞)be geodesic ray with γ(0)=P,and be the Buseman function associated to γ.From comparison theorem,bγis a pluri-subharmonic function.Moreover,by a standard convolution technique or heat equation deformation on bγ(1.2),we obtain a smooth strictly pluri-subharmonic function u of linear growth:
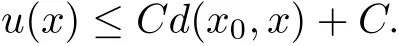
Theorem 1.4 follows from calculating the Monge-Ampere measure

and integration by parts([17]).The proof of Theorem 1.5 is a little involved.It based on the following L2-estimates ofoperator(see[1,19]):
Theorem 1.6(Andreotti-Vesentini[1],Hömander[19]) On a complete Kähler manifold(M,ω),suppose we have a function ϕ,a Hermitian holomorphic line bundlewith curvature(1,1)-form C1()such that
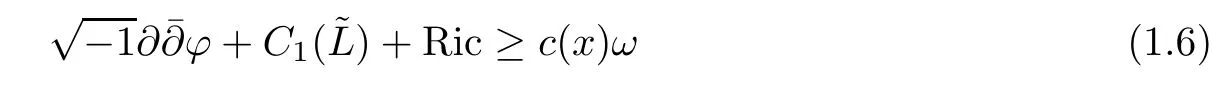
where c(x)is a positive function on M,ω the Kähler form;suppose we also have a-closed-valued(0,1)form f on M such that

Then the equation

admits a smooth solution u(section of)such that
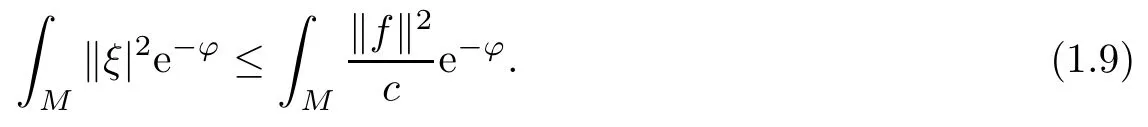
Take L=K be the canonical line bundle,then C(L)=−Ric.On some coordinate system|z|<1 around a point P,choose ϕ=Cu+log|z|2n+2be a strictly psh weight function,then(1.6)holds.Choosefor some smooth compact supported section of L which is holomorphic near P and non-vanishing at P.Then the above L2estimate gives a nontrivial holomorphic section E=S−ξ of L satisfying

On the other hand,the Poincare-Lelong equation:
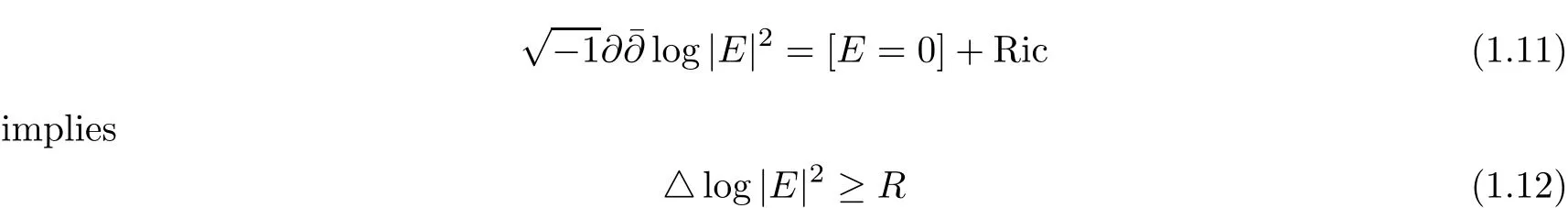
holds in the sense of distributions.The integral average of R over geodesic balls can be derived from the growth of E(see[17]).
Theorem 1.5 is crucial in proving the maximal volume growth condition is preserved during the Ricci flow(see[4,14]).It yields that the volume growth ratio of the manifold at in finity remains invariant.We know that this ratio is monotonically decreasing as the radius goes to in finity,which follows from the volume comparison theorem since Ric≥0.
2 Maximal Volume Growth
The first breakthrough was made by Mok[26].
Theorem 2.1(Mok[26]) Let M be a complete non-compact Kähler manifold of complex dimension n with positive holomorphic bisectional curvature.Suppose there exist positive constants C1,C2such that for a fixed base point x0,
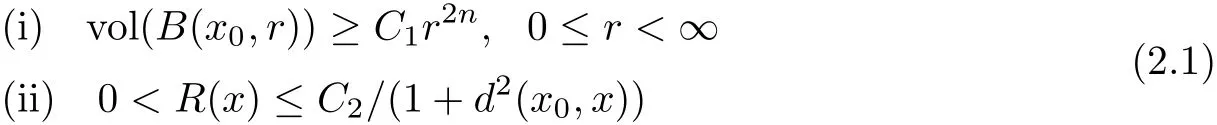
then M is biholomorphic to an affine algebraic variety.Moreover,if in addition the complex dimension n=2 and(iii)the Riemannian sectional curvature of M is positive,then M is biholomorphic to C2.
We recall brie fly the scheme of Mok’s proof.We consider the algebra P(X)of holomorphic functions of polynomial growth and its quotient field R(X)of“rational functions”.We use the solution of(1.4)and L2-estimates(Theorem 1.6)to prove there are many functions in P(X).Then,we prove Siegel’s theorem for R(X),i.e.,R(X)=C(fI···fn;g/h)is a finite extension field of a purely transcendental extension of C of degree n.We do this by establishing a multiplicity estimate for P(X).Then,we use Skoda’s L2-estimates for the ideal problem to prove the “almost-surjectivity”of F=(f1···fn,g,h)of X into an affine algebraic variety.By establishing a uniform multiplicity estimate(i.e.,independent of base points)for P(X),we prove a finiteness theorem for desingularizing F.Finally we use the convexity of X with respect to P(X)to complete F to a proper embedding.
In[34],Shi obtained the following
Theorem 2.2(Shi[34]) Let M be a complete non-compact Kähler manifold of complex dimension n with bounded and positive holomorphic bisectional curvature.Suppose there exist positive constants C1,C2such that for a fixed base point x0,

then M is biholomorphic to a pseudo-convex domain in Cn.
In[34],Shi initiated the study of Ricci flow on Yau’s uniformization conjecture.He proved that,under the conditions(i)(ii)in his theorem,the Kähler condition,the positivity of bisectional curvature and the maximal volume growth are all preserved.Moreover,he showed that Ricci flow exists for all time t>0,and the curvature decays to zero as t→∞in the following way(Theorem 8.7 in[34]):

Using the estimate(2.3),Shi proved that there is a smooth positive function u(t)∈C∞[0,∞),such thatwill converge in C∞− topology to a flat Kähler metric.Because it is not known whether the limit is complete,Shi could only conclude that the manifold is a pseudo-convex domain(see also[16]).
In complex dimension 2,in[14],an affirmative answer to Yau’s uniformization conjecture under the maximal volume condition was obtained:
Theorem 2.3(Chen-Tang-Zhu[14]) Let M be a complete non-compact Kähler manifold of complex dimension 2 with bounded and positive holomorphic bisectional curvature.Suppose there exist a positive constant C1such that for a fixed base point x0,
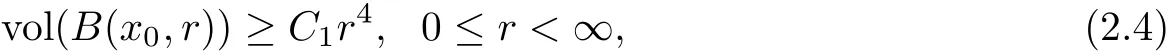
then M is biholomorphic to C2.
Our proof of the theorem consists of three parts.In the first part,we showed that M is a Stein manifold homeomorphic to R4.Since the maximal volume growth condition is preserved(with same constant,Theorem 1.5),we proved that the curvature of the evolving metric decays linearly in time,via a blow up and blow down argument:

This implies that the injectivity radius of the evolving metric is greater thanand any geodesic ball with radiusis pseudoconvex.From this,one can show that Mnis a Stein manifold homeomorphic to R4.
In the second part,we considered the algebra P(M)of holomorphic functions of polynomial growth on M and we proved that its quotient field has transcendental degree 2 over C.For this,we first need to construct two algebraically independent holomorphic functions in the algebra P(M).Using the L2estimates in Theorem 1.6,it suffices to construct a strictly plurisubharmonic function of logarithmic growth on M.If the scalar curvature decays in space(at time t=0)at least quadratically as in Theorem 2.1,it was known that such a strictly plurisubharmonic function of logarithmic growth can be obtained by solving the Poincare-Lelong equation(1.4).But we do not assume the curvature decay condition.Here the novel idea is to transform the time decay estimate(2.5)of evolving metrics to the space decay at t=0,via apriori estimates for(nonlinear)heat equations.Roughly speaking,the time decay estimate(2.5)of evolving metrics implies that the curvature of the initial metric must decay quadratically in space in certain average sense:
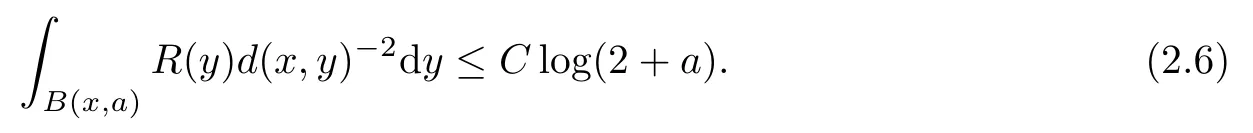
The apriori estimate is obtained from integrating the following equation in space and time:

(2.6)turns out to be enough to solve the Poincare-Lelong equation(1.4)to find a strictly pluri-subharmonic function u of logarithmic growth,
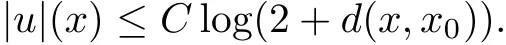
In the last part,we basically followed the approach of Mok[26]to establish a biholomorphic map from M onto a quasi-affine algebraic variety,by desingularizing certain holomorphic mapping F:M→Z from M to a quasi-affine algebraic variety Z.The essential point is to establish uniform estimates on the multiplicity and the number of irreducible components of the zero divisor of a holomorphic function of polynomial growth.Again,the time decay estimate 2.5 of the Ricci flow plays a crucial role in the arguments.Based on these estimates,we showed that the mapping F:M→Z is almost surjective in the sense that it can miss only a finite number of subvarieties in Z,and can be desingularized by adjoining a finite number of holomorphic functions of polynomial growth.This completes the proof that M is a quasi-affine algebraic variety.Finally,by combining with the fact that M is homeomorphic to R4,we concluded that M is indeed biholomorphic to C2by a classical theorem of Ramanujam on algebraic surfaces.
In 2006,Chau-Tam[4]extended the above theorem to higher dimensions:
Theorem 2.4(Chau-Tam[4]) Let M be a complete non-compact Kähler manifold of complex dimension n with bounded and nonnegative holomorphic bisectional curvature.Suppose there exists a positive constant C1such that for a fixed base point x0,

then M is biholomorphic to Cn.
A result due to Rosay-Rudin([33])and its generalization by Varolin([37])on attractive basins say the following:Let F be a biholomorphism from a complex manifold Nnto itself and let p∈Nnbe a fixed point,andbe the basin of attraction of p.Suppose Ω contains an open neighborhood of p.Then Ω is biholomorphic toThis result was used by Chau-Tam in[6]to prove that a gradient Kähler Ricci soliton is biholomorphic to Cnif it is either steady with positive Ricci curvature and the scalar curvature achieves its maximum at some point,or expanding with nonnegative Ricci curvature.The gradient Kähler Ricci soliton involves a family of biholomorphisms φtin its de finition,pick one of them(for t>0,so that it is shrinking)to be F in the result of Rosay-Rudin-Varolin([33]and[37]).For more general solutions of Kähler Ricci flow,one usually only have local biholomorphisms,instead of one particular global biholomorphism F.
We give a sketch of the proof of Theorem 2.4 in[4].They used Ricci flow to deform the initial metric.As explained before,the Kählerity,nonnegativity of bisectional curvature,maximal volume growth(same constant)are preserved by the Ricci flow as long as the curvature of the solution is bounded.The first crucial thing is to prove that the curvature decays linearly in time,i.e.,(2.5).If the curvature operator is nonnegative,in[17],we proved that(2.5)still holds for all dimensions n by using a blowing up and blowing down argument as in[14].In[31],Ni proved(2.5)holds when bisectional curvature is nonnegative.Letsatis fies a new equation for all t∈(−∞,∞).The estimate(2.5)implies that the curvature of˜g(t)is uniformlly bounded independent of t.
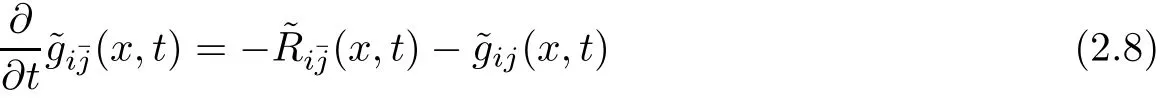
Combining with the maximal volume growth, fix a point P∈M,we have a uniform injectivity radius estimate for allat P.From standard L2-estimate,there is a fixed r>0 such that for each i∈ N,one can construct a holomorphic map Φi:B(r)→ M,where B(r)=is the ball of the radius r in the Euclidean space,such that Φiis a biholomorphic map onto its image Φi(B(r))which contains a geodesic ball of radiusaround P of the metric.Moreover,is close to the Euclidean metric.Fix a large N,let Fibe a family of biholomorphisms from B(r)onto its image which is inside B(r)such thatTo imitate the proof of Rosay-Rudin-Varolin’s result([33]and[37]),one should prove that asymptotically this family of Fibehaves close to a single map F.The authors observed that the eigenvalues of Ricci curvature ofis non-decreasing(it is bounded from above by the estimate),and for any sequence tk→ ∞,the solutionbehave close to a Kähler Ricci soliton.Cao’s Li-Yau-Hamilton inequality[2]and[3]plays a key role in the argument.Here,the idea is that the closeness of the solution with Kähler Ricci soliton is enough to imply the closeness of the family of Fito some single map F.For more details,we refer to[4]and the survey[5].
In a preprint“On Yau’s uniformization conjecture” arXiv:1606.08958,Liu[23]claimed that he could remove the boundedness of the curvature assumption in Chau-Tam’s theorem[5]:
Theorem 2.5(Liu[23]) Let M be a complete non-compact Kähler manifold of complex dimension n with nonnegative holomorphic bisectional curvature.Suppose there exists a positive constant C1such that for a fixed base point x0,
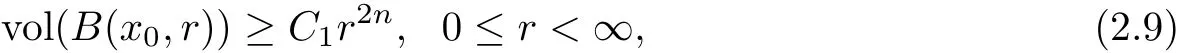
then M is biholomorphic to Cn.
Liu introduced some new ideas with three circles theorems and Cheeger-Colding theory,see[23–25].In[24],he proved that the ring of holomorphic functions of polynomial growth on a complete manifold with nonnegative bisectional curvature is finitely generated,and such a manifold is affine provided it has maximal volume growth,con firming another conjecture of Yau.
On the other hand,in a recent paper Lee-Tam[22],Lee-Tam proved that on a complete noncompact K−ahler manifold with nonnegative bisectional curvature and maximal volume growth,the K−ahler-Ricci flow exists at least for a short time,and it preserves all these conditions,more importantly,the curvature becomes bounded for t>0.Combining with the previous result in Chau-Tam[4],this yields an alternative proof of Yau’s uniformization conjecture for the maximal volume growth case.
3 Non-maximal Volume Growth
As we have seen,there are important progress on Yau’s uniformization conjecture for manifolds with maximal volume growth.Nevertheless,many examples of positively curved Kähler manifolds with non-maximal volume growth were discovered.It is likely that non-maximal volume growth is typical for complete Kähler manifolds with positive bisectional curvature.
For Conjecture 1.1,the non-maximal volume growth case has also been considered in the literatures(see[18,36]).In[36],W.K.To considered the compacti fication of complete manifolds with non-maximal volume growth,motivated by the work of Mok[27],Mok-Zhong[30].He assumed the finiteness of the first Chern number and the condition of a mixture of the curvature decay and volume growth,more precisely:
Theorem 3.1(To[36]) Let X be an n-dimensional noncompact complete Kähler manifold of positive Ricci curvature and of finite topological type.Suppose for some base point x0∈X that there exist positive constants k1,k2,k3and a positive real number p such that for a>0
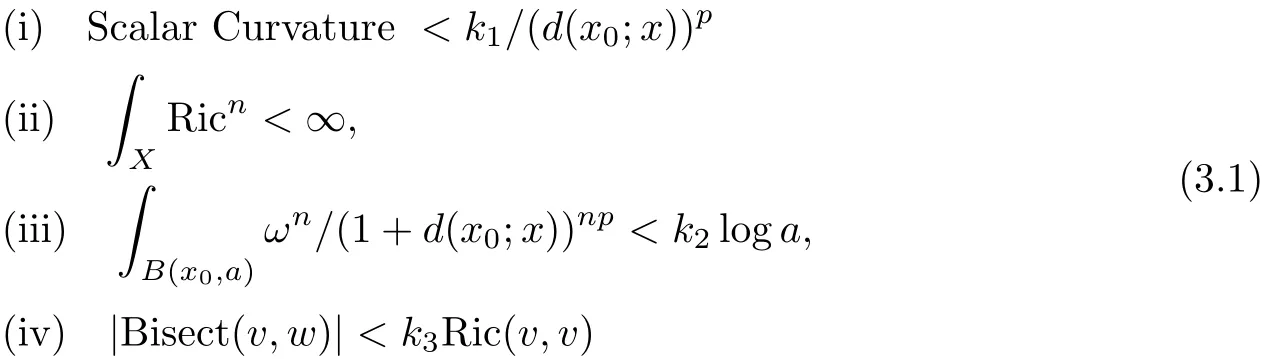
for all unit tangent vectors v,w ∈ T′(X)and x ∈ X.Then X is biholomorphic to a quasiprojective variety.Moreover,if p≥2,the theorem is valid without assuming condition(iii).
Corollary 3.2(To[36]) Let X be a two-dimensional noncompact complete Kähler manifold of positive sectional curvature.Suppose X satis fies conditions(i),(ii),and(iii)of the above theorem.Then X is biholomorphic to C2.Moreover,if p>2,the corollary is valid without assuming condition(iii)of the Theorem 3.2.
In[18],we proved that when sectional curvature is positive and bounded,the finiteness of the Chern numberis sufficient to ensure that the manifold is quasi-projective.
Theorem 3.3(Chen-Zhu[18]) Let Mnbe a complete noncompact Kähler manifold with bounded and positive sectional curvature,and
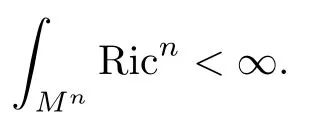
Then Mnis biholomorphic to a quasi-projective variety.In the case of complex dimension n=2,M2is biholomorphic to C2.
4 Finite Chern Numbers
Note that in Kähler geometry,positive sectional curvature is stronger than positive bisectional curvature.
More precisely,we will prove the following:
Theorem 4.1Let Mnbe a complete Kähler manifold with bounded sectional curvature and positive Ricci curvature.Suppose Mnadmits a Hermitian holomorphic line bundle L such that the curvature C1(L)of L is positive and bounded and satis fies

Combining Theorems 3.3 and 4.1,we get the following:
Corollary 4.2Let Mnbe a complete noncompact Kähler manifold with bounded and positive sectional curvature.Suppose Mnadmits a Hermitian holomorphic line bundle L such that the curvature C1(L)of L is positive and bounded and satis fies
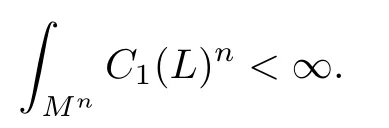
Then Mnis biholomorphic to a quasi-projective variety.In the case of complex dimension n=2,M2is biholomorphic to C2.
Several remarks are in order.
Remark 4.3Let Mnbe a complete Kähler manifold with bounded sectional curvature and positive Ricci curvature.Suppose Mnadmits a strictly pluri-subharmonic function ϕ such thatis bounded and
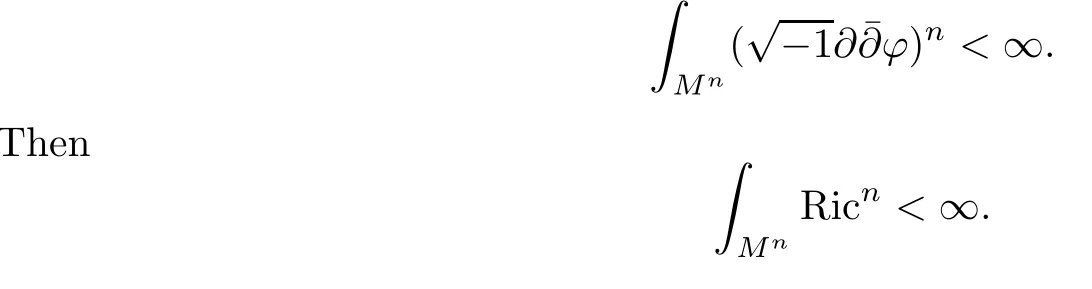
This can be obtained by taking L to be the trivial line bundle M×C equipped with the Hermitian metric e−ϕ.
Remark 4.4Let Mnbe a complete Kähler manifold with bounded positive bisectional curvature.Suppose Mnhas minimal volume growth in the sense of Theorem 1.4,i.e.,there exists x0∈Mnand C>0 such that
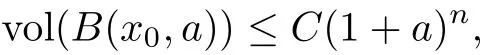
for all a>0,where n is the complex dimension of the manifold.Then
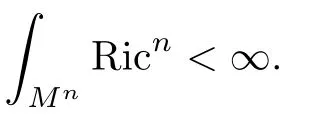
This can be obtained in the following way.It is well-known the Buseman function on this manifold is a pluri-subharmonic function with Lipschitz constant 1.Making use of the heat equation deformation of the Buseman function,we get a smooth strictly pluri-subharmonic function ψ with bounded gradient.The boundedness ofis ensured by the Bernstein estimate.is derived from the minimal volume growth condition(see[17]).
5 Proof of Theorem 4.1
Let M be a complete Kähler manifold,L a Hermitian holomorphic line bundle with positive curvaturelocal holomorphic coordinates around x0,z1(x0)= ···=zn(x0)=0;e be a local holomorphic section(nowhere vanishing on1 be a smooth cuto fffunction onSince C1(L)>0,we may choose sufficiently large positive integer p0such that

The integrability forces uito vanish at x0at least to the 2nd order,i.e.,ifnontrivial holomorphic section of Lp0⊗K.We summarize the results in the following proposition:
Proposition 5.1Let M be a complex n-dimensional complete Kähler manifold,L a Hermitian holomorphic line bundle with positive curvature C1(L)>0 on M.Then for any x0∈M,there exists positive integer p0and n nontrivial holomorphic sections siof Lp0⊗K such that
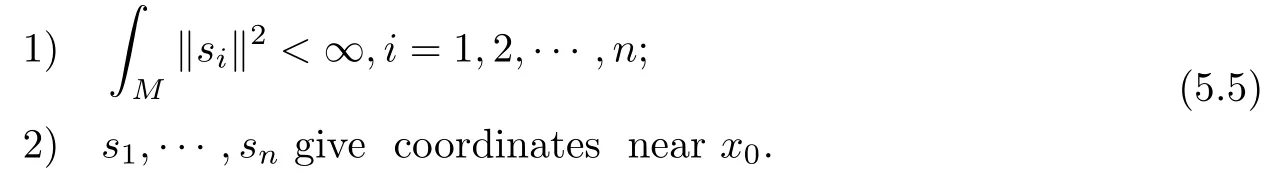
Let M and the line bundle L be assumed as in Theorem 4.1.Fix x0∈M.Denote by Γ(Lp0⊗K)the space of L2− integrable holomorphic sections of Lp0⊗K.For s∈ Γ(Lp0⊗K),direct computations lead to
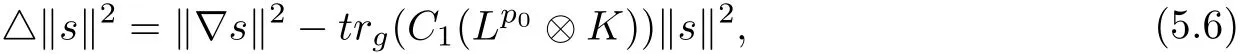
where trg(C1(Lp0⊗K))=p0trg(C1(L))−R is bounded by our assumption.
Multiplying both sides of(5.6)by a cut-o fffunction,integrating by parts,and making use of Cauchy-Schwarz inequality,we have

Applying mean value inequality to(5.6),we have
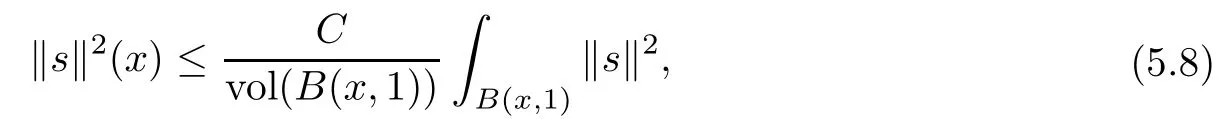
where we used the boundedness of trg(C1(Lp0⊗K)).By volume comparison theorem,we have vol(B(x,1))≥ (1+d(x,x0)2n)−1vol(B(x0,1)),hence

where C may depend on s and x0.
For applications in sequel,we need to fix an auxiliary function ψ on Mnwhich may be used to construct cut-o fffunctions.ψ satis fies
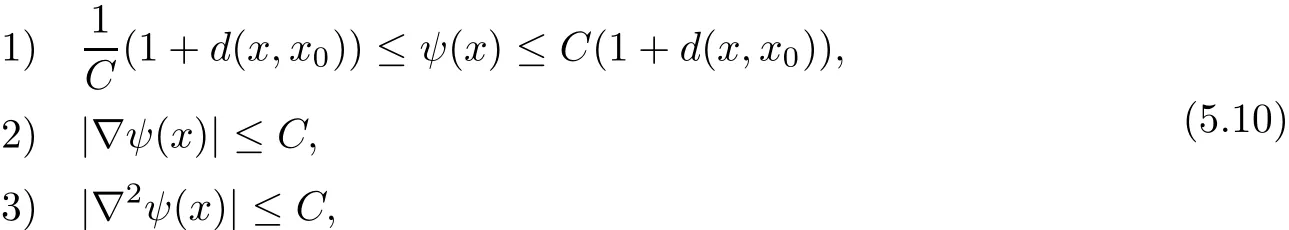
where C is some constant depending only on the curvature bound.The easiest way to construct ψ is smoothing the distance function by convolutions in a suitable ball(of tangent space)of uniform size.

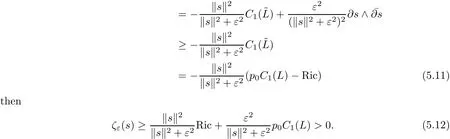
Proposition 5.2For anyhave
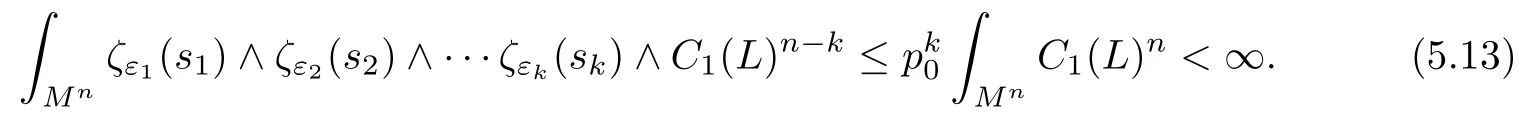
Theorem 4.1 is a corollary of Proposition 5.2.
Proof of Theorem 4.1Take n nontrival sections s1,s2,···,sn∈ Γ(L⊗p0⊗ K),(this is possible by Proposition(1.6),and let ε1,ε2,···,εk→ 0,the limitinf of the left hand side of(5.13)is not less thanRMnRicnby(5.12).Hence
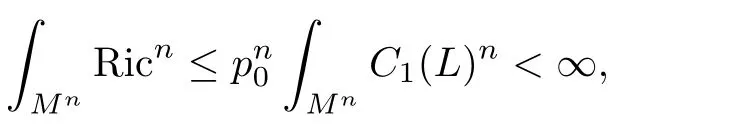
and the Theorem 4.1 is proved.
So we only need to show Proposition 5.2.The method is a modi fication of the standard Bezout estimate(see[18,27,36]).First of all,we need a lemma:
Lemma 5.3For anywe have
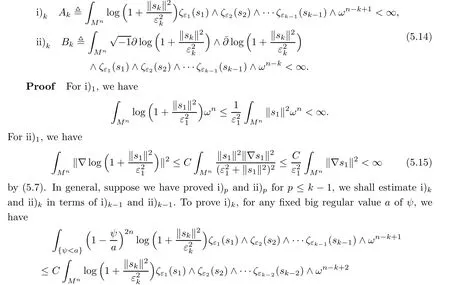
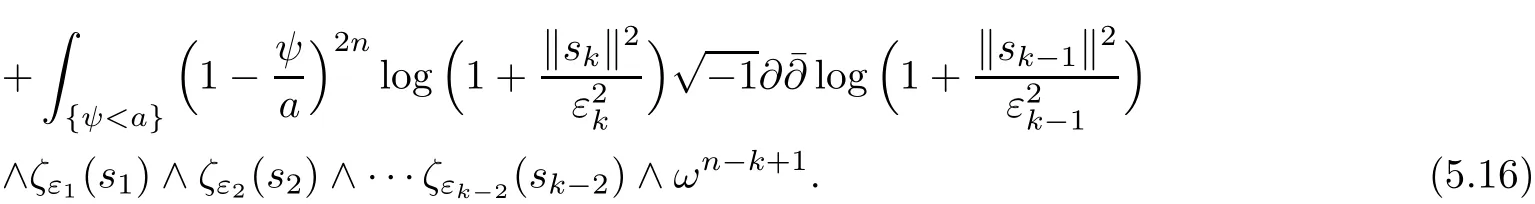
The first term in the right hand side of(5.16)is just i)k−1.Integrate by parts the second term and use Cauchy-Schwarz,it can be controlled from above by

where we have used(5.10).The first and second terms in(5.17)are controlled by ii)k−1.By(5.10)(5.9)and induction assumption i)k−1,the third term in(5.17)can be controlled from above by

Taking a sequence of regular values a → ∞ of ψ,we find the third term of(5.17)converges to zero,and we have estimated i)kby i)k−1and ii)k−1.
To derive ii)k,we consider
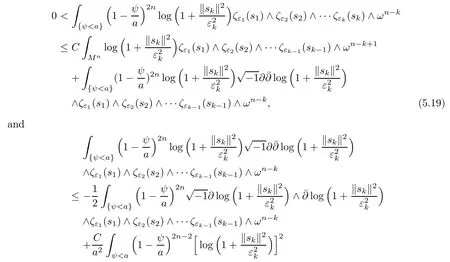
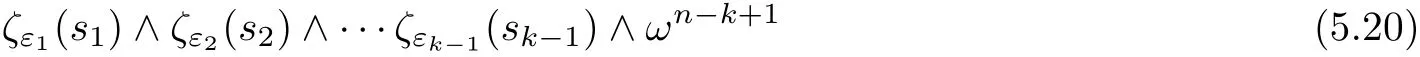
by integration by parts and Cauchy-Schwarz.Combining(5.19)and(5.20),we get
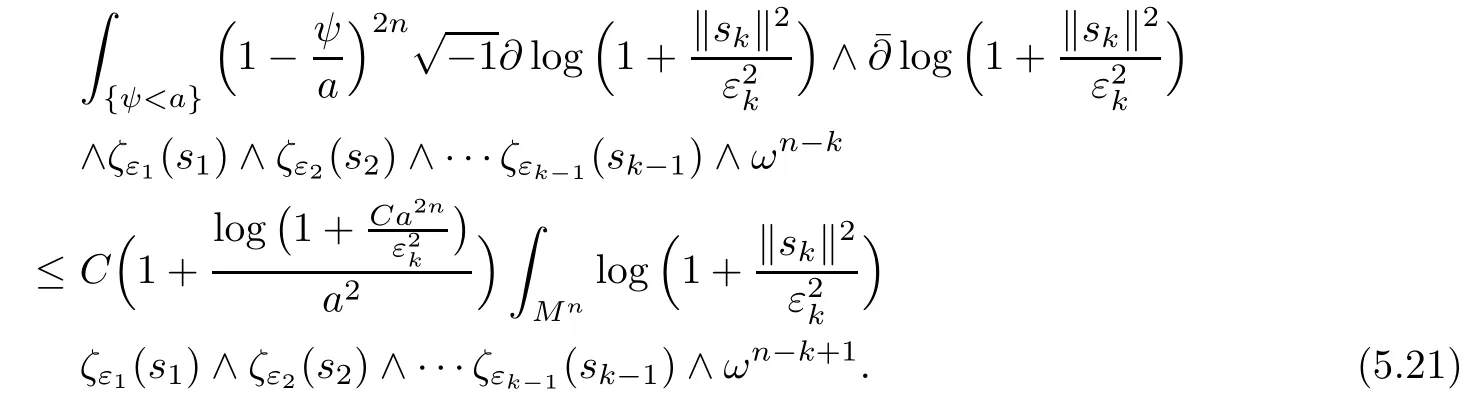
Taking a sequence of a→∞,we have estimated ii)kin terms of i)k,i.e.,
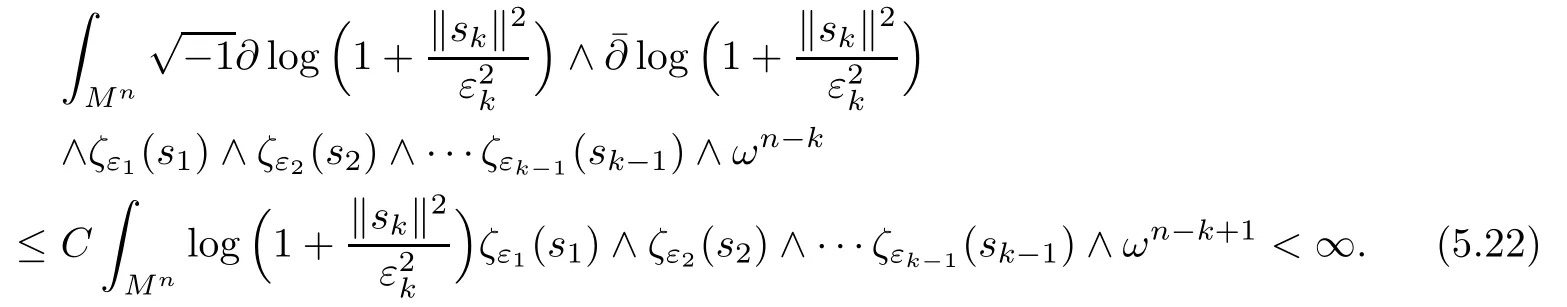
The proof of the lemma is completed.
Now we are ready to prove Proposition 5.2.
Proof of Proposition 5.2The case k=0 is trivial.When k=1,for any big regular value a of ψ,we have
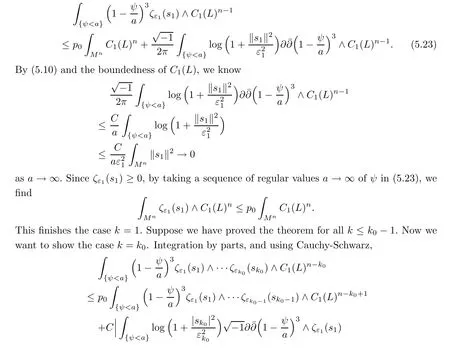

 Acta Mathematica Scientia(English Series)2018年5期
Acta Mathematica Scientia(English Series)2018年5期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARIZATION OF PLANAR VORTICES FOR THE INCOMPRESSIBLE FLOW∗
- STABILITY OF STEADY MULTI-WAVE CONFIGURATIONS FOR THE FULL EULER EQUATIONS OF COMPRESSIBLE FLUID FLOW∗
- ONE-DIMENSIONAL VISCOUS RADIATIVE GAS WITH TEMPERATURE DEPENDENT VISCOSITY∗
- MACROSCOPIC REGULARITY FOR THE BOLTZMANN EQUATION∗
- RADIAL SYMMETRY FOR SYSTEMS OF FRACTIONAL LAPLACIAN∗
- STRONG COMPARISON PRINCIPLES FOR SOME NONLINEAR DEGENERATE ELLIPTIC EQUATIONS∗
