半变系数伽马脆弱模型惩罚部分似然估计
张 中 文, 王 晓
( 1.大连理工大学 数学科学学院, 辽宁 大连 116024;2.滨州医学院 公共卫生与管理学院, 山东 烟台 264003 )
0 引 言
脆弱模型是比例风险模型的推广,是考虑随机效应的生存分析模型.其中,随机效应(即脆弱)一般用于描述对应于不同分类(例如个体或家庭)的额外风险或者脆弱,其基本思想是不同的个体具有不同的脆弱,相对比较脆弱的个体与其他个体相比更容易发病或死亡.近年来,脆弱模型被广泛应用于研究对象之间存在不可观测的组间异质性的非独立生存时间问题的研究;同时,多种脆弱模型以及拟合这些模型的数值技术被广泛研究,例如:为了增加模型的灵活程度、扩大模型的应用范围,Du等提出了一种非参数带脆弱项的危险率模型[1];Yu等将多元对数正态脆弱模型推广到可加半参数情形用以描述协变量对于对数危险率的非线性影响,并提出了一种双惩罚部分似然法用于模型的估计[2],该模型在增加了模型适应性的同时,也避免了多元非参数函数的估计问题.
变系数模型是近年来发展起来的具有广泛应用背景的回归模型,该模型通过假设回归系数是其他协变量的未知函数而增加模型的灵活性,因为系数函数通常被假设为某个协变量的一元函数,所以维数灾难问题得到了有效避免.如Zhang等研究了半变系数多元脆弱模型的估计问题,用以描述某些协变量对于危险率的影响受其他协变量的影响,并通过数值模拟和实例分析说明了方法的有效性,其中脆弱的分布假定为对数多元正态分布[3].而在实际的脆弱模型应用过程中,假定脆弱服从伽马分布更为常见,这是因为伽马分布的变量为正数,十分适合脆弱分布无符号改变的特性;伽马分布可以通过Laplace变换获得导数,从而使得整个模型求导具备相对的简便性.本文提出一种半变系数伽马脆弱模型,以进一步丰富脆弱模型的模型结构,用以描述聚集生存数据或者复发型生存数据分析中协变量效应受其他协变量的影响,从而为分析生存时间与协变量更准确、更复杂的关系提供方法学支持.
1 半变系数伽马脆弱模型

λij(t;xij,uij,wij,νi)=
λ0(t)νiexp(βT(uij)xij+αTwij)
(1)
式中:λ0(t)是基准危险率函数;同时νi(i=1,2,…,s)表示第i个聚类中的脆弱,并且服从单参数伽马分布,其概率密度函数为
(2)
若令ri=logνi,可称ri为随机效应,则半变系数伽马脆弱模型亦可改写为
λij(t;xij,uij,wij,ri)=
λ0(t)exp(βT(uij)xij+αTwij+ri)
(3)
假设生存时间Tij与删失时间Cij关于协变量、随机效应ri条件独立,不同个体的生存时间关于随机效应条件独立,同时假设随机效应与删失时间相互独立.
2 模型估计方法
2.1 B-样条
变系数函数向量β(u)可以通过基函数为{B1(u),B2(u),…,Bm(u)}的B-样条进行估计,其中m指样条基函数的个数,样条基函数的数量和形状是由节点个数和位置决定的.本研究在模拟和实例分析过程中选择m=5.
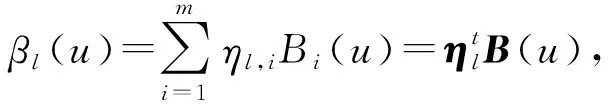
η1,2…η1,mη2,1η2,2…η2,m…ηp1,1
ηp1,2…ηp1,m)T,并将协变量取值与对应的样条基函数相乘记为gij=(x1,ijBT(uij)x2,ijBT(uij) …xp1,ijBT(uij))T,则第i个聚类中第j个个体在给定νi以及其他协变量条件下的风险函数可以近似转化为
λij(t;xij,uij,wij,νi)≈λ0(t)νiexp(ηTgij+αTwij)=
λ0(t)exp(ηTgij+αTwij+ri)
(4)
2.2 惩罚部分似然估计
本文首先在假定θ已知的条件下,采用惩罚部分似然法给出协变量参数的估计,同时随机效应也假定为回归参数进行估计[4].其中,惩罚函数选择随机效应的负对数似然函数,由νi的分布可知,ri服从对数伽马分布,密度函数为
(5)
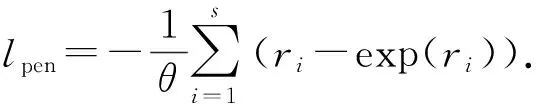
进一步可以给出半变系数伽马脆弱模型的惩罚部分似然函数:
lPPL(α,η,r)=lpart-lpen=
αTwij+logνi)-
(6)
类似于线性伽马脆弱模型[5],对于固定的θ,可以通过最大化lPPL(α,η,r)获得α、η、r的估计值.估计过程中,首先假定r为固定效应的回归系数,然后分别关于α、η、r求lPPL(α,η,r)的得分方程:
(7)
(8)
(9)
其中h=1,2,…,s,且当i=h时,zij,h=1,否则zij,h=0.通过调整各项的排列方式,式(9)可以改写为
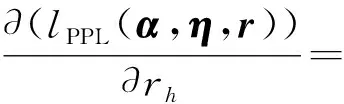
αTwhj+rh)Λ0(yhj)+
(10)
其中
(11)
由牛顿迭代法求解得分方程,可以给出估计α、β、r,进而可以采用Nelson-Aalen法得到基准危险率的估计量λ0.
2.3 随机效应参数的估计
在假设α、η、r已知的条件下,本文采用近似轮廓似然法估计θ.首先,对于固定的α、η,建立边际似然函数如下:
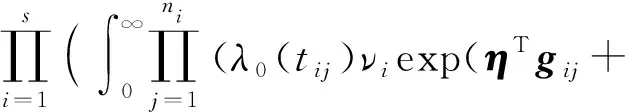
αTwij))δijexp(-Λ0(tij)νiexp(ηTgij+
(12)
利用伽马函数的性质(或者应用Laplace变换)[6],经过适当计算、整理,均可将边际似然函数改写为
(13)
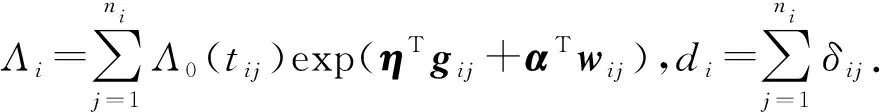
(14)
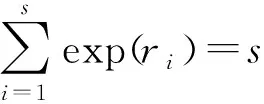
(15)
利用黄金搜索算法可以得到式(15)的最大值,从而给出随机效应方差成分的估计θ.
2.4 模型估计流程归纳
现将整个估计流程归纳如下:第1步,运用B-样条生成新的协变量Gi;第2步,在给定θ初始值的条件下,利用Newton-Raphson算法求解惩罚对数部分似然函数的最大值,从而给出α、θ、r;第3步,对于上一步得到的α、θ、r,通过极大化式(15)得到θ;接下来不断重复第2步和第3步直到收敛,最后给出α、η、θ最终的估计.

3 数值模拟
本文通过数值模拟的方式对提出的模型及其估计方法进行评价.模拟分为2个部分:(1)所有协变量的系数均是常数系数情形生成的数据集;(2)协变量系数部分为变系数、部分为常数系数情形生成的数据集.考察的模型是半变系数伽马脆弱模型,其模型结构为
λij(t;xij,uij,wij,νi)=λ0(t)νiexp(β(uij)·
xij+α·wij);
i=1,2,…,s,
j=1,2,…,ni
模拟中,每个聚类中个体的个数(ni)为5,样本量分别设定为100、300、500,则对应的聚类个数(s)分别为20、60、100;删失率分别设定为10%、30%、50%,实际删失率的误差控制在0.5%以内;不同情形下,每种模拟的次数设定为500次;删失时间被设定为服从指数分布,模拟中通过调整指数分布的参数控制删失率;另设λ0(t)=t,脆弱项νi~Γ(1,1),即方差(θ)为1的伽马分布,xij~exp(1),wij~N(1,1);常数系数α=1,协变量u在区间(1,3]内按样本量大小等距取点,在模拟1中β(u)=1,在模拟2中β(u)=cos(2u)+1.
3.1 模拟1
模拟1用于说明本文提出的方法是否适用于所有协变量系数均为常数的情形.不同条件下α、θ的模拟结果见表1.

表1 β(u)=1条件下模型参数的模拟结果
由表1可见,不同条件下α的估计误差均非常小,即使在删失率达到50%,而聚类个数仅为20个时,估计偏差也仅为0.034;α标准误的估计方面,经验标准误Semp均略高于估计标准误Sest,这与相关文献中的研究结果一致[2-3,7].不同删失率条件下,标准误均随着样本量的增大而减小,而相同样本量条件下,标准误随着删失率的升高而增大.在样本量较小时,θ的估计误差相对较大,删失率的提高会造成θ估计误差的增大,在样本量为500时,删失率的提高对于θ估计的影响较小.
模拟1中,β(u)的估计及其95%置信带见图1.篇幅原因,未将样本量为300或者删失率为30%的情况显示,其各自的估计效果介于对应的不同样本量和删失率之间.
由图1可见,不同条件下,β(u)的估计效果均较好,特别是当样本量为500时,β(u)和β(u)的曲线几乎是重合的;95%置信带的曲线形状与β(u)基本一致,只是边界有略大的波动,这与文献结果一致[2-3,8],置信带的宽度随着样本量的增大而变窄;β(u)的估计偏差同样受样本量的影响,样本量越大,估计偏差越小;在模拟过程中考察的删失率范围内,即10%~50%,β(u)的估计偏差无明显变化,这体现出了本文方法对于不同的删失率具备一定的稳健性.
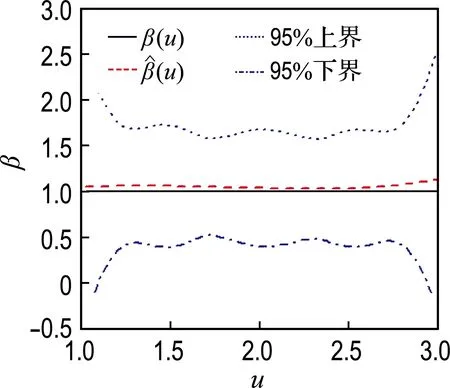
(a) 删失率10%,样本量100
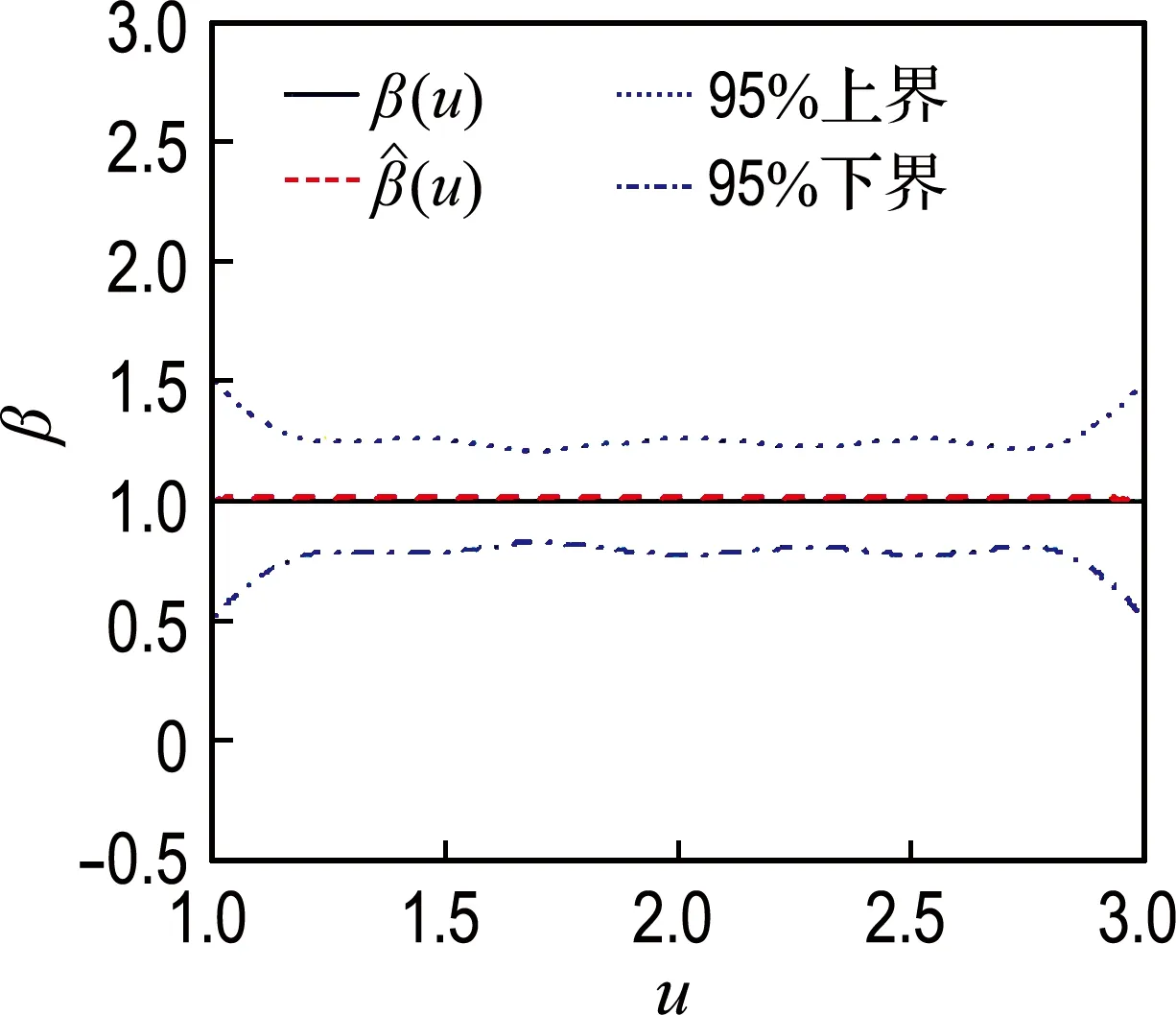
(b) 删失率10%,样本量500
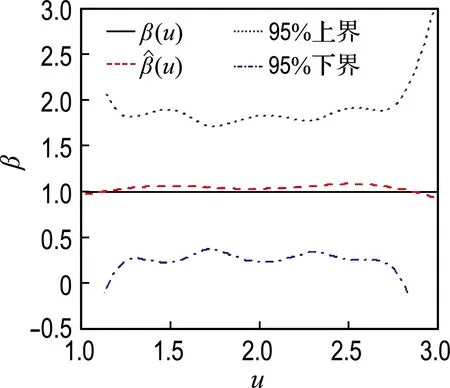
(c) 删失率50%,样本量100
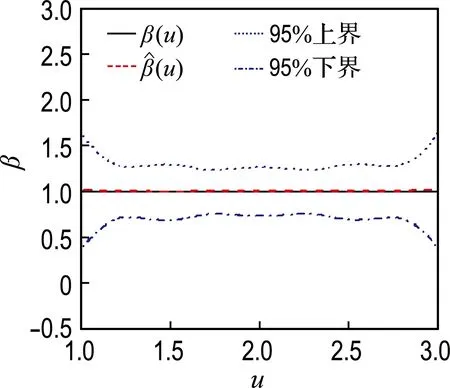
(d) 删失率50%,样本量500
图1β(u)=1时不同样本量和删失率条件下β(u)的估计
Fig.1 Estimation ofβ(u) in the condition ofβ(u)=1 based on different sample number and censor rate
3.2 模拟2
模拟2用于评价本文提出的方法在半变系数伽马脆弱模型条件下的拟合效果.不同条件下α、θ的模拟结果见表2.β(u)的估计及其95%置信带见图2.
由表2可知,与模拟1的结果类似,不同条件下α的估计误差仍然都比较小,即使在删失率达到50%,而聚类个数仅为20个时,估计偏差仍旧不大;α标准误的估计方面,经验标准误也均略高于估计标准误,这与相关文献中的研究结果一致[2-3,7].对于固定的删失率水平,样本量的增大可以带来估计标准误和经验标准误的减小;与此同时,对于固定的样本量,估计标准误和经验标准误也随着删失率的提高而略有增大.在样本量较小同时删失率又较高时,θ的估计误差相对较大,模拟中最大平均误差达到近0.14;在样本量较小时,删失率的提高会造成θ估计误差较明显的增大,而在样本量较大时,删失率的提高对于θ估计的影响不再显著.
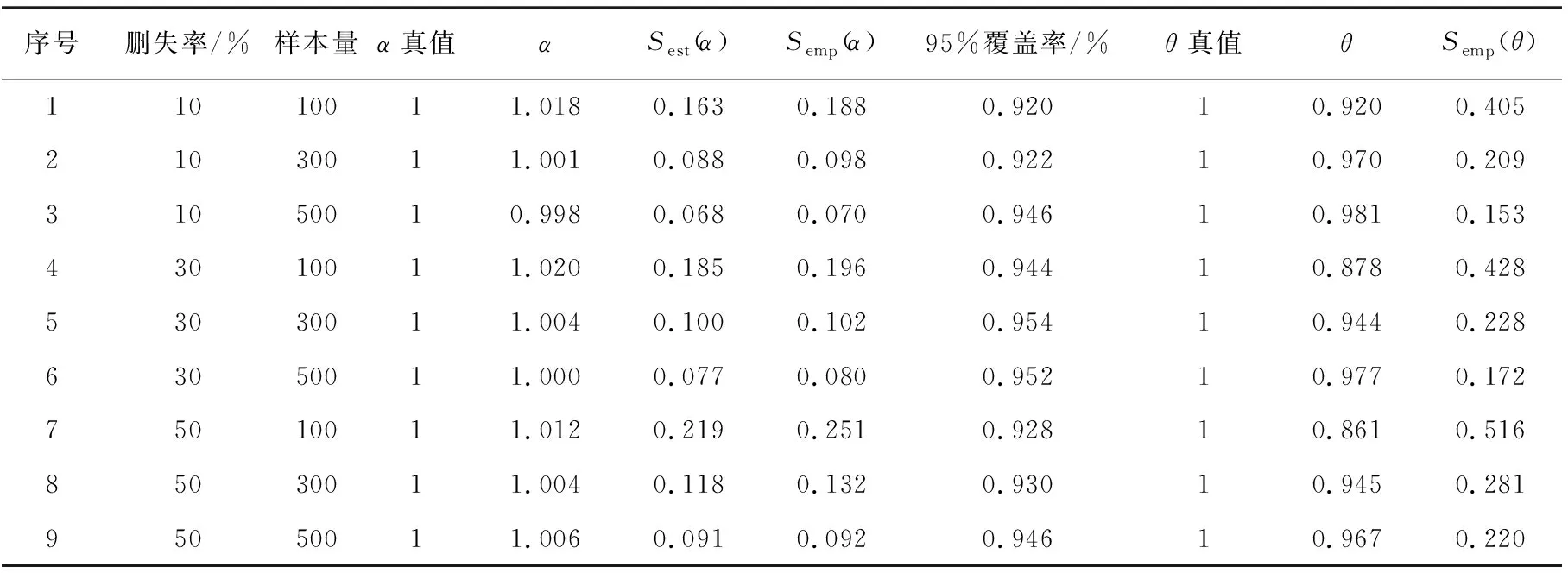
表2 β(u)=cos(2u)+1条件下模型参数的模拟结果
由图2可知,对应于不同的样本量和删失率,β(u)的平均估计均比较准确,尤其是在样本量较大(500)时,β(u)和β(u)的图像几乎是重合的.与模拟1类似,95%置信带的曲线形状与β(u)基本一致,只是在边界处有相对较大的波动,置信带的宽度随着样本量的增大而变窄;β(u)的偏差同样受样本量的影响,样本量越大,偏差越小;在模拟过程中考察的删失率范围内,即10%~50%,β(u) 偏差的变化并不显著,模拟2和模拟1共同体现出了本文提出方法是比较稳健的.
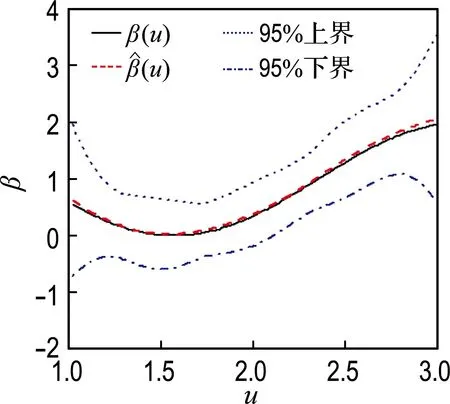
(a) 删失率10%,样本量100

(b) 删失率10%,样本量500
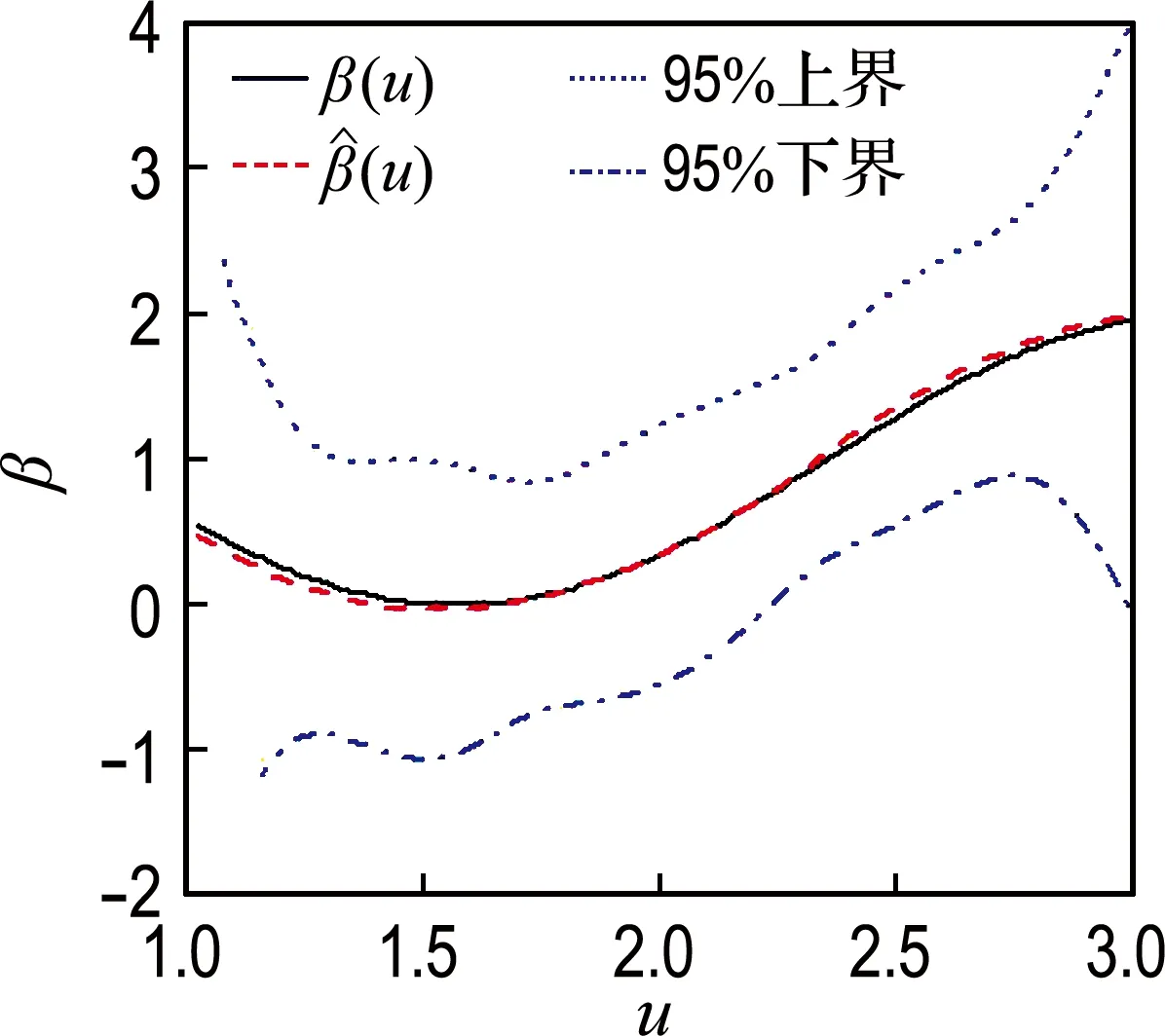
(c) 删失率50%,样本量100
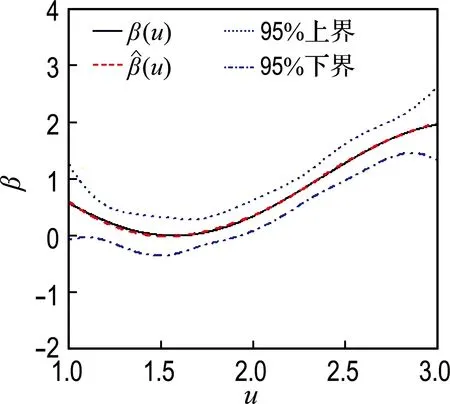
(d) 删失率50%,样本量500
图2β(u)=cos(2u)+1时不同样本量和删失率条件下β(u)的估计
Fig.2 Estimation ofβ(u) in the condition ofβ(u)=cos(2u)+1 based on different sample number and censor rate
4 实例分析
本文通过分析美国北部癌症治疗中心(North Central Cancer Treatment Group,NCCTG)的晚期肺癌数据来评价本文提出的模型与方法的应用效果.调查涉及167名晚期肺癌患者,删失率为28%,文献中已经有关于本数据集的一些分析[9-10],本研究重点考察病人Karnofsky自评分对于危险率的影响受其他因素的影响情况,了解晚期肺癌的预后因素,从而为医师以及病人制订更合理的治疗方案提供参考.所谓预后是指预测疾病的可能病程和结局,它既包括判断疾病的特定后果,如康复,某种症状、体征和并发症等其他异常的出现或消失及死亡,也包括提供时间线索,如预测某段时间内发生某种结局的可能性.
纳入本研究的评价指标包括机构代码(I)、生存时间(T)、删失指标(C)、病人年龄(U)、病人的Karnofsky自评分(X)、性别(W1)、ECOG得分(W2)、卡路里摄入量(W3).考虑到不同医疗机构的治疗水平存在差别,即考虑病人的生存时间在就医机构方面表现出聚集性,即具有不可观测的随机效应,因而将这些变量代入半变系数伽马脆弱模型,模型结构如下:
λij(t;νi,uij,xij,w1,ij,w2,ij,w3,ij)=
λ0(t)νiexp(β(uij)xij+α1w1,ij+
α2w2,ij+α3w3,ij)
(16)
采用本文提出方法给出各协变量的估计,同时采用bootstrap方法给出95%置信带的估计,结果显示,性别以及ECOG得分对于危险率的影响具有统计学意义,男性相比女性危险率更高,ECOG得分越高,危险率也越高,详见表3.
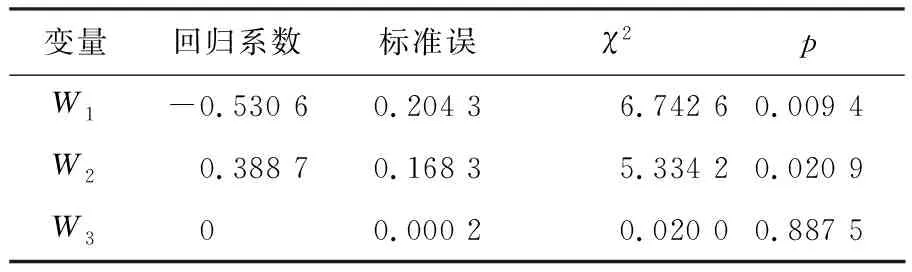
表3 NCCTG数据回归参数的估计
图3显示,不同年龄段晚期肺癌患者的Karnofsky自评分对对数危险率的影响大小非常数,而是一个非线性函数.
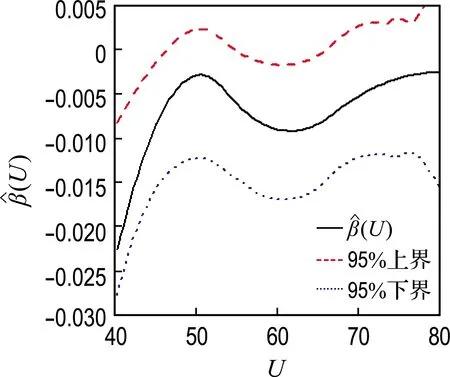
图3 NCCTG数据分析中变系数函数及其置信带的估计
Fig.3 Estimation of the varying coefficient function and confidence belt of NCCTG data
5 结 语
经模拟研究和实例分析发现,在样本量不大的条件下,本文提出的方法即可给出模型线性回归系数非常准确的估计,删失率的提高也不会对参数的估计效果造成明显影响.在样本量较小同时删失率又较高的条件下,随机效应参数的估计误差较大,这提示在实际的应用过程中本方法有低估随机效应方差的倾向,当样本量较大时,随机效应参数的估计误差则会明显减小.本文提出的方法可以给出常数函数非常准确的估计,即适用于所有系数均为线性回归系数的场合,也即本文的方法包含传统的线性伽马脆弱模型作为其特殊形式;同时,本文提出的模型可以给出非线性函数系数非常准确的估计,这也扩展了伽马脆弱模型的适用范围和应用领域.
综上所述,本文提出的方法对传统的伽马脆弱模型进行了有效的扩展,方法稳定、计算速度也较快,常数回归系数以及函数回归系数的估计对样本量和删失率的要求均不高,适宜在实际问题中推广使用.当然,本研究中也存在一些不足,例如:虽然在模拟研究中给出了变系数函数的置信带,在实例分析中也应用bootstrap方法给出了变系数函数的置信带,但未能就函数系数的假设检验等问题进行探讨,这也有待于接下来更深入的研究.

