在错解中理解圆与方程 于纠错中提升思辨能力
——求解圆与方程问题的典型错误辨析
朱贤良
(安徽省枞阳县宏实中学 246700)
在解题活动中,“错误”总是遭人讨厌,却又似乎挥之不去、如影随形.事实上,只要我们能正确地对待错误,利用好这一宝贵的资源,在错误中反思、感悟,就一定可以悟出真相、悟出规律、悟出本质、悟出智慧.以圆与方程为例,笔者总结了常见的四类错误,在学习中妥善加以利用,既有助于我们理解圆与方程的相关知识,又能在纠错中不断提升思辨水平.
一、忽略圆的一般方程中的隐含条件
例1 已知圆x2+y2+k2x+y-k=0关于直线y=x对称,求k的值.

辨析由于方程x2+y2+k2x+y-k=0是否为圆的方程尚没有保证,故此时谈不上它关于直线y=x的对称问题.当且仅当D2+E2-4F>0,即k4+1+4k>0时,方程x2+y2+k2x+y-k=0为圆的方程,在此条件下再研究它关于直线y=x对称才有意义.
正解因为方程x2+y2+k2x+y-k=0表示圆,故D2+E2-4F=k4+1+4k>0(*).

当k=1时,(*)式成立,符合题意;
当k=-1时,(*)式不成立,故舍去.
所以,k=1.
例2 已知圆C的方程为x2+y2+kx+2y+k2=0,要使过点A(1,2)所作圆的切线有两条,求k的取值范围.
错解因为过点A(1,2)作圆C:x2+y2+kx+2y+k2=0的切线有两条,故点A在圆C的外部,即9+k+k2>0,解得k∈R.
辨析我们不能在没有D2+E2-4F>0保证的前提下,去讨论圆x2+y2+Dx+Ey+F=0的任何性质特征.正如同说二次方程x2-2x+10=0的两个实根之和为x1+x2=2、两个实根之积为x1x2=10一样,这是极其荒谬的,因为没有Δ≥0的保证,二次方程不一定有实根.因此,在平常的学习中,要重视对概念、定理的本质进行准确把握,不可死记硬背、生搬硬套.

又过点A(1,2)作圆C的切线有两条,故点A在圆C的外部,即9+k+k2>0,解得k∈R.……②
二、对两圆相切的位置关系考虑不全
例3 求半径为4,与圆x2+y2-2x-4y+4=0相切,且和直线y=0相切的圆的方程.
错解结合图形可判断,所求圆的圆心必在x轴的上方.
因为所求圆与直线y=0相切,且半径为4,故可设圆心坐标为O1(a,4),则方程为(x-a)2+(y-4)2=16.
已知圆x2+y2-2x-4y+4=0,即(x-1)2+(y-2)2=1,其圆心为O2(1,2),半径为1.
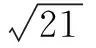
辨析两圆相切的情况有两种,到底是外切还是内切,或是两者皆有可能,一般可以通过作图进行分析、判断.在两圆内切时,还需要注意区分哪一个圆在外,哪一个圆在内.两圆相切可分为内切与外切,错解并未分析全面,仅考虑了外切这一种情形.
正解结合图形可判断,所求圆的圆心必在x轴的上方.因为所求圆与直线y=0相切,且半径为4,故可设圆心坐标为O1(a,4).而已知圆x2+y2-2x-4y+4=0,即(x-1)2+(y-2)2=1,其圆心为O2(1,2),半径为1.由两圆相切,可知O1O2=4+1=5(外切)或O1O2=4-1=3(内切).
三、忽略切线、交线的特殊位置情形
例4 求过原点且与圆(x-1)2+(y-2)2=1相切的直线方程.
错解因为所求直线过原点,可设其方程为y=kx,即kx-y=0.
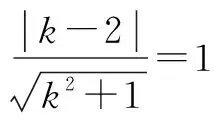
辨析本题考查直线与圆的位置关系,一般都通过圆心到直线的距离与半径的大小关系加以判断.但在设直线方程时,没有考虑斜率不存在这一特殊情况,即易犯漏解这样的错误.本题中,原点在圆(x-1)2+(y-2)2=1外部,故过原点必可作该圆的两条切线,上述解答有误.

(2)当直线的斜率不存在时,其方程为x=0.此时,圆心(1,2)到直线x=0的距离恰好为圆的半径1,故也符合题意.


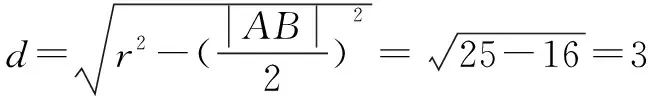

辨析在运用直线的点斜式方程包括斜截式方程解题时,常会发生类似的错误,这是点斜式方程和斜截式方程本身的局限性所致.在这两类方程里,没有包含斜率不存在的直线.因此,用这两类方程解题时,必须验证斜率不存在的直线是否符合题意的要求.
正解(1)当直线l的斜率存在时,同错解得直线l的方程为3x+4y+15=0.

综上所述,所求直线方程为3x+4y+15=0或x=-3.
四、未检验曲线与方程的关系
例6 已知圆C的方程为x2+y2=9,过点P(5,0)作直线l与圆C交于A,B两点,求弦AB中点M的轨迹方程.
错解显然直线l的斜率必定存在,可设其方程为y=k(x-5).
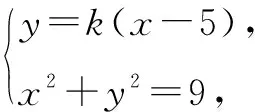
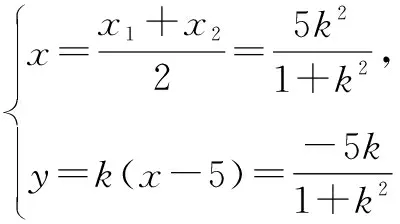
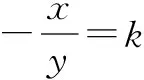
当k=0时,x=y=0,也满足方程x2+y2-5x=0.
所以,M的轨迹方程为x2+y2-5x=0.
辨析过圆外一点的直线与圆相交是有条件的,这个条件显然应当限制轨迹方程中变量x,y的范围.本题只能保证轨迹上的点的坐标都是方程x2+y2-5x=0的解,但不能保证以方程的解为坐标的点都在曲线上,所以x2+y2-5x=0不是M的轨迹方程.
正解同错解得点M(x,y)的坐标满足方程x2+y2-5x=0.
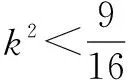
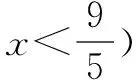
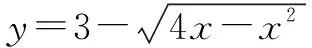
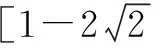
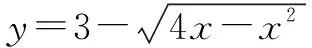
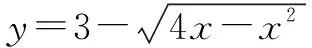
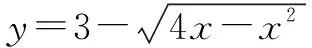
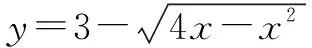
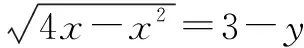
⟺4x-x2=(3-y)2(y≤3)
⟺(x-2)2+(y-3)2=4(y≤3)
此方程表示一个圆的下半部分,圆心坐标为(2,3),半径为r=2.
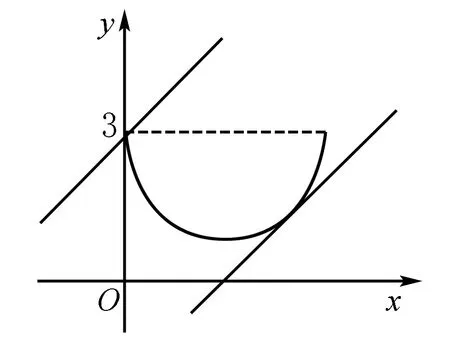


错误总是伴随着人认识事物的整个过程,也只有从错误中不断总结,才能认识真相、掌握真理.因此,在学习过程中,既要注意养成良好的解题习惯与思维习惯,对一些常见的错误产生预见性并合理规避,进而提升自身的“免疫力”,更要善于辨析错误,从中汲取智慧.

