一类变系数波方程耦合系统局部解的适定性
兰 杰
(山西财贸职业技术学院,山西 太原 030031)
0 引言
本文研究的是变系数波方程耦合系统:
(1)
其中Ω⊂Rn(n≥2)是具有光滑边界∂Ω的有界区域,a,b>0,p>1,q>2是常数.A(x)=(aij(x))为正定的对称矩阵,aij(x)是Rn中的光滑函数.我们关注的是系统(1)局部解的适定性.
在实际应用中,系统(1)表示一类波方程[1,2],可以表示有关噪音控制的实际问题.这类问题在文献[1]中提出,并在文献[2]中进行了发展.而波方程解的适定性,在文献[3-5]中都进行了广泛的讨论.
文章主要是运用黎曼几何[4,5]和乘子方法[3,4],在对p,q合适的假设下,对系统(1)局部解的适定性进行讨论并得到结论.本文的核心内容分为以下两部分,在第二部分中,引入了黎曼流形中一些符号表示,提出本文证明中需要的一些假设条件,并给出文章的主要结论;第三部分是对证明所需要引理进行引入并且证明,最后证明了本文的主要结论,即系统(1)局部解的适定性.
1 准备工作和主要结论
下面我们引入黎曼流形中的一些符号表示
令G(x)=(gij(x))=A-1(x),∀x∈Rn


(2)
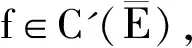
gf=A(x)f
我们对系统(1)作出如下假设:
(A1)存在θ>0使得
∀0≠ξ=(ξ1,ξ2,…,ξn)T∈R2,
(3)
(A2)p,q满足:
(4)
(5)
并定义能量泛函如下:
(6)
其中
令
定义系统(1)的稳定集如下:
S:={(u,v)∈H0'(Ω)×H0'(Ω):I(u,v)>0}∪{0,0}
则我们有如下主要结论:
定理1(局部解的适定性)假设(A1)-(A2)成立,则对任意的
(u0,v0)∈H0'(Ω)×H0'(Ω),(u1,v1)∈L2(Ω)×L2(Ω)
系统(1)在[0,T]上存在唯一的局部解(u,v)满足
(u,v)∈(C([0,T]),H0'(Ω)×H0'(Ω)))∩Lp(Ω×(0,T))
(ut,vt)∈(C([0,T]),L2(Ω))2∩Lp(Ω×(0,T))2.
2 主要结论的证明
2.1 证明主要结论需要引入的重要引理并对其进行证明
引理1假设p满足(4)式(u0,v0)∈S,(u1,v1)∈L2(Ω)×L2(Ω)满足
E(t)是一个非增函数,则(u,v)∈S,∀t∈[0,T)并且有
(7)
证明 由(u0,v0)∈S,故存在t0∈(0,T],使得I(u,v)≥0,∀t∈[0,t0],则由I(u,v),J(u,v)的定义可知

由J(u,v)和E(t)的定义可知,J(u,v)≤E(t);
由于E(t)是非增函数,故E(t)≤E(0),∀t∈[0,∞);
∀t∈[0,t0]
(8)
则根据H0'(Ω)|→L2p(Ω),(3),(7)式及Young不等式,得


(9)
故(u,v)∈S,∀t∈[0,t0]又因为
故重复以上过程,可得到存在t1>t0,使得
并且有(u,v)∈S,∀t∈[0,t1]
故重复以上过程若干次,即可将结论延拓到[0,T]上去.
2.2 主要结论的证明
定理1的证明
证明 由引理1可得,(u,v)∈S,∀t∈[0,T],故

由连续性原理即可得
假设(A1)-(A2)成立,则对任意的
(u0,v0)∈H0′(Ω)×H0′(Ω),(u1,v1)∈L(Ω)×L(Ω)
系统(1)在[0,T]上存在唯一的局部解(u,v)满足
(u,v)∈(C([0,T]),H0′(Ω)×H0′(Ω)))∩Lp(Ω×(0,T))
(ut,vt)∈(C([0,T]),L2(Ω))2∩Lp(Ω×(0,T))2.

