强化数学思想方法，提升几何探究能力

（福建省上杭县旧县中学 福建上杭 364214）

中考试题凝聚着命题专家的智慧，在复习阶段适当选用或者改编中考试题，让学生在探究活动中体验图形变化、几何直观、特殊化与一般化、分类讨论、化归等几何探究的基本思想方法，并在总结反思中提炼，在迁移训练中自觉运用，能提高复习效率，也有助于丰富数学思想方法，提升学生的几何探究能力。 下面笔者以一道中考数学压轴题为例，谈谈这方面的体会。

题目：在正方形ABCD中，对角线AC、BD交于点O，点P在线段BC上（不含点B），

（1）当点P与点C重合时（如图1）.求证：△BOG≌△POE；

（3）把正方形ABCD改为菱形，其他条件不变（如图3），若∠ACB = α，求的值（用含α的式子表示）.

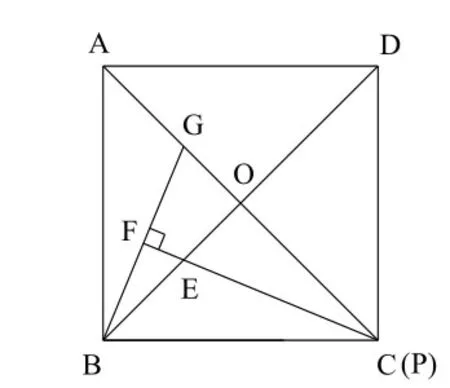
图1

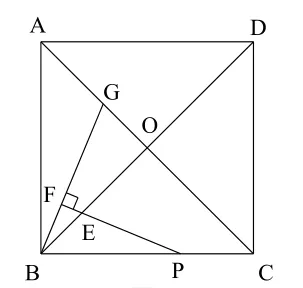
图2

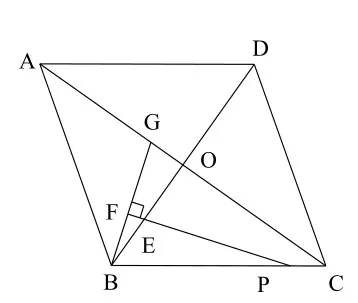
图3

一、改编试题

如图2，在正方形ABCD中，对角线AC、BD交于点O，点P在线段BC上（不含点B），PE交BO于点E，过点B作BF⊥PE，垂足为F，交A C于点G.试探究：的值，证明你的结论，并将命题进行推广。

设计意图：近年来，不少中考试题的设计都从特殊情况开始探究，再进一步拓展到一般情况；或是先限定在某一范围内探究结论成立的情况，再拓展到其他范围，进一步判断其结论是否也成立.其用意在于考查学生对特殊到一般思想方法的理解和运用水平以及对于数学拓展研究的能力.然而这种思想方法已经被命题者用来设计问题了，学生只需按照命题者的要求，解答一个个小问题就可以，与命题者的初衷相去甚远。

二、解法探究

1.审题

（1）仔细阅读题目，并在图形上标注已知条件和能简单得到的结果，如图4；

（2）认真观察图形，寻找图形特征并分离出基本图形△BCG.

2.猜想

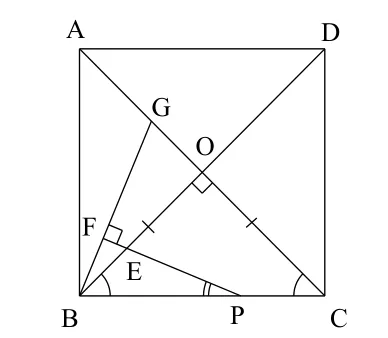
图4

图5

（2）特殊化：让点P与点C重合，如图5 ，此时△BPG为等腰三角形，同时Rt△BOG≌Rt△POE，∴BG = PE，从而

3.证明思路

思路1：寻找特殊情形的本质特征

图5的特征在于等腰三角形中含有全等三角形，据此在图4中过点P作PM // AC交BG于M，交BO于N，如图6，这样构造出与图5类似的图形△BPM.

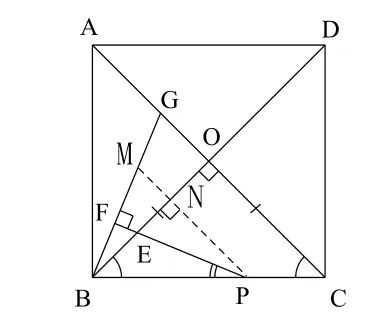
图6

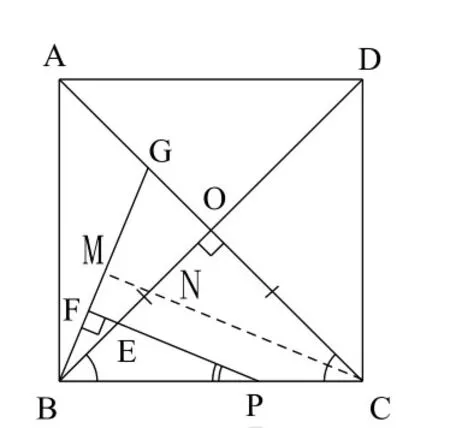
图7

思路2：寻找一般情形与特殊情形之间的联系

比较图4与图5，图4中仍有等腰△BPG，为构造出特殊情形的图形，可过C作CM // EP交BG于M，交BO于N。由特殊情形知：而这可由图7中CM // EP得到，即有得到。

4.拓展

（1）突破某一范围的条件限制

如去掉“点P在线段BC上（不含点B）”的限制，会有怎样的结果？通过画图可知，此时仍有等腰三角形中含全等三角形的结构，结论依然成立。从而可推广为：“点P为线段BC延长线上一点，其余条件不变时，结论仍然成立”，如图8，证明思路与前面的完全一样。

（2）改变题目背景

将题目中的条件弱化，如正方形变为特殊平行四边形，经过探究可得：

如图9，把正方形ABCD改为菱形，其他条件不变，若∠ACB =α，求的值（用含α的式子表示）.

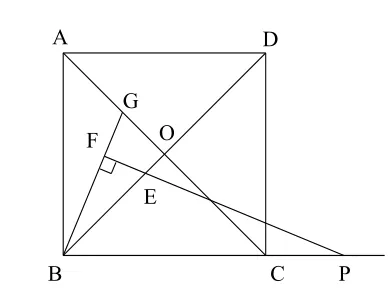
图8

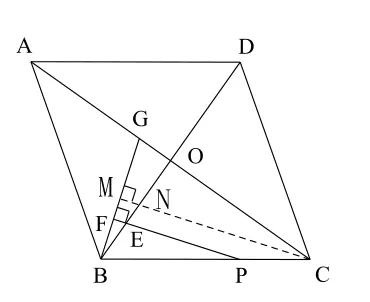
图9

思路分析:

因为推广过程中保持了原题的等腰△BCG结构，所以证明的思路也与原来类似。 如过点C作CM // EP交BG于M，交BO于N，由于此时∠ACB ≠∠CBO，所以△ONC与△BOG也就不全等了，也即≠ ，但BM = BG仍能成立，所以有只要求出就可以了，由Rt△ONC∽Rt△BOG可得而在Rt△BOC中，所以，

还有其它的证明方法吗？（让学生课后再思考）

三、反思总结

数学思想方法是数学学科的精髓，是将数学知识转化为数学能力的桥梁。由于数学思想方法属于隐性知识，是以具体的知识为载体，因而对数学思想方法的掌握更多地体现在对解题策略的思考和选择上。

华罗庚先生说过，解题时先足够地退，退到我们最易看清问题的地方，认透了，钻深了，然后再上去.他认为这是学好数学的一个决窍.因此，以特殊问题为起点，抓住数学问题的特征（如本题等腰三角形中含全等三角形），通过逐步分析、比较，层层深入，揭示规律，由此得到证明的基本思路。对一般化下的问题，可采取“化归”的办法：或抓住特殊化时图形的本质特征，什么变了，什么没有变，紧紧抓住末变的；或将一般化下的情形转化为特殊化情形，看两者之间有何联系，由此得到一般化情况下的证明思路（如本题等腰三角形中含相似三角形）.先特殊化，解决特殊情形下的问题，再一般化，寻求一般问题与特殊问题之间的联系，将一般问题进行化归，这是初中几何一种重要的数学思想方法。

四、迁移应用

1。如图10，已知点P是Rt△ABC斜边AB上一动点（不与A，B重合），分别过A、B向直线CP作垂线，垂足分别为E、F，Q为斜边AB的中点.当点P在线段AB上不与点Q重合时，试判断线段QE与QF的数量关系，给予证明并对该命题进行推广。

图10

图11

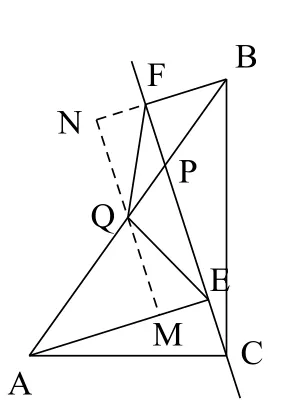
图12

注：先特殊化，若点P与点Q重合，则由△AQE≌△BQF可得QE = QF。再一般化，受特殊化中利用三角形全等进行证明的思路启发，延长FQ交AE于点D，证明△AQD≌△BQF得QD = QF，再根据Rt△FDE中QE为斜边FD的中线，得到QE = QF，如图11；或过点Q作EF的平行线分别交AE、BF于点M、N，证明△AQM≌△BQN得QM = QN，再证△EQM≌△FQN得QE = QF，如图12。

推广：当点P在线段BA或AB的延长线上时，结论仍然成立。

2.如图13，在Rt△ABC中，∠C = 90°，D为AB中点，点M、N分别在BC、AC边上，且DM⊥DN，作MF⊥AB于点F，NE⊥AB于点E.试探究AE和DF的数量关系，并加以证明，最后将该命题进行推广。

注：先特殊化，若AC = BC，且DM⊥BC，DN⊥AC，得到图14，显然AE = DF。其次一般化，在图14中先去掉条件DM⊥BC，DN⊥AC，如图15，再去掉条件AC = BC ，如图13，此时AE≠NE，但从图中可以看出△NED和△MFD也不全等，受基本图形的启发，可得到△NED∽△MFD（全等可看着相似的特殊情况，或作DN′⊥AC，DM′⊥BC，此时有△DN′N∽△DM′M，如图15），进而有又△NEA∽△MFB，可得再由线段比例关系的换算可得出结论。

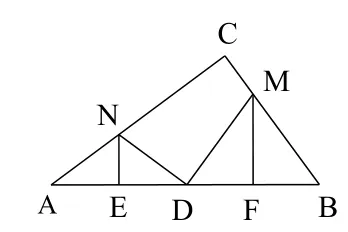
图13

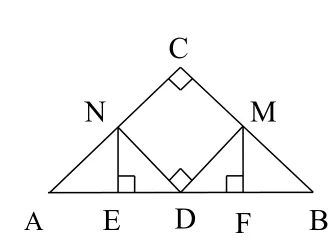
图14

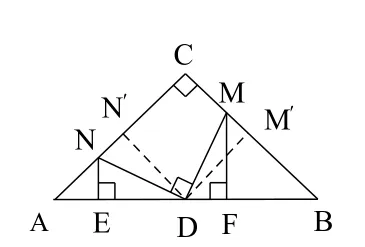
图15

推广：若BD = kAD（k为任意正整数），条件中的“点M在BC上”改为“点M在线段CB的延长线上”，其它条件不变，则有AE =kDF。

利用上述改编的中考试题，可以让学生将不变的数学思想方法置身于变化的题目之中，通过类比迁移，强化基本的数学思想方法，使学生学会以“不变”应“万变”，真正达到举一反三的效果，从而提高几何探究能力。