利用导数运算法则和单调性构造函数解题

（齐齐哈尔中学 黑龙江齐齐哈尔 161000）

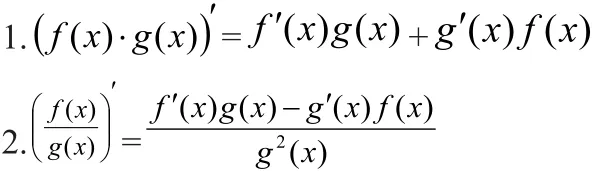
近几年的练习、高考题频频的出现，凸显了此类题目的炙热程度，实质上就是导数运算法则的形式的逆用、体现了题根源于教材。高中阶段常用模型如下：

一、利用函数求导的四则运算构造函数

1.设函数f′(x)是奇函数f(x) (x∈R)的导函数，f(−1)=0，当x＞0时，xf′(x)-f(x)＜0，则使得f(x)＞0成立的x的取值范围是（ ）

A.(− ∞ ,− 1 )U ( 0,1) B.(− 1 ,0)U(1,+ ∞)

C.(− ∞,− 1 )U ( −1,0) D.(0 ,1)U (1 ,+ ∞)

答案：A

2.设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x＜0时f′(x) ⋅g(x)+g′(x) ⋅f(x)＞0，且g(3)=0，则不等式f(x)⋅g(x)＜0的解集（ ）

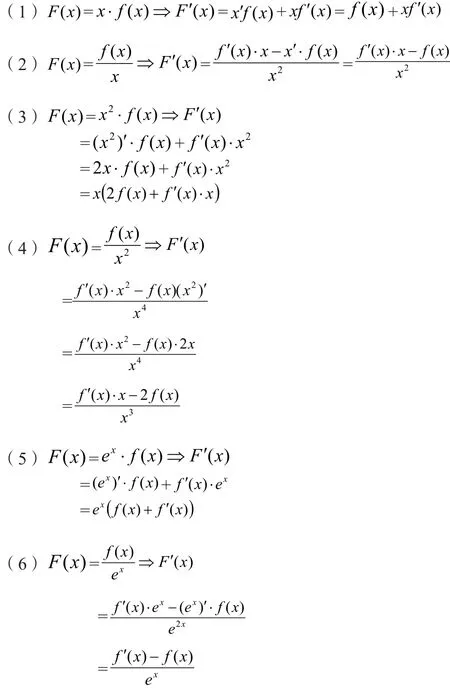
A.(− 3,0)∪ ( 3,+ ∞) B.(− 3 ,0)∪(0,3)

C.(− ∞ ,− 3)∪(0,3) D.(− ∞,−3)∪(3,+∞)

答案：C

3.已知f(x)为定义在(− ∞ ,+ ∞ )上的可导函数，f(x)＞f′(x)对于x∈R恒成立，且e为自然对数的底数

A.e2013⋅f(2014) ＜e2014⋅f(2013)；

B.e2013⋅f(2014)=e2014⋅f(2013)；

C.e2013⋅f(2014) ＞e2014⋅f(2013)；

D.e2013⋅f(2014)与e2014⋅f(2013)大小不确定；答案：A

4.已知函数f(x)是偶函数，f′(x)是它的导函数，当x＞0时，f(x)+x⋅f′(x)≤0恒成立，f(−2)=0，则不等式x⋅f(x)＜0的解集为.

解：设F(x)=x⋅f(x)⇒F′ (x)

=x′⋅f(x)+f′(x)⋅x

=f(x)+f′(x)⋅x

由F(x)=x⋅f(x)∴F( −x)

=−x⋅f(−x)

=−xf(x)=−F(x) ∴F(x)为奇函数，其图像关于原点对称当x＞0时，f(x)+x⋅f′(x)≤0∴F(x)在(0,+ ∞)上单调递减，f(−2)=0∴F(−2)=0=F(2)∴x∈(−2,0)∪(2,+ ∞)

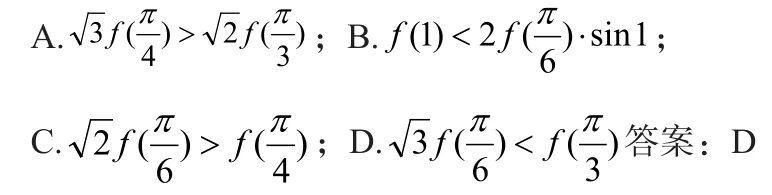
6.设函数f(x)是定义在(− ∞ ,0 )上的可导函数，其导函数为f′(x)，且有2f(x)+x⋅f′(x) ＞x2。

则不等式(x+2014)2⋅f(x+2014)−4f(−2)＞0的解集为（ ）

A.(− ∞ ,− 2 012)；B.(−2012,0)；

C.(− ∞ ,− 2 016)；D.(−2016,0)

答案：C

7.已知定义在R上的函数f(x)，满足3⋅f(x)＞f′(x)恒成立，且f(1)=e3（e为自然对数的底数）则下列结论正确的是（ ）

A.f(0)=1；B.f(0)＜1；

C.f( 2)＜e6；D.f( 2)＞e6

答案：C

二、利用函数单调性构造函数

1.已知R上的奇函数f(x)满足f′(x)＞ −2，

则不等式f(x−1)＜x2⋅(3−2l nx)+3(1−2x)的解集为.

解：设F(x)=f(x−1)-x2⋅ (3− 2 l nx)-3(1−2x)

则F′(x)=f′(x−1)+4xl nx-4x+6

再设g(x)=4xlnx-4x+6，

则g′(x)=4 l nx(x＞ 0 )， 当g′(x)＞0时 即l nx＞ 0 ⇒x＞1，∴g(x)在x∈(0,1)递减，在(1,+ ∞ )递增。

∴x=1时，g(x)min=g(2)=2∴F′ (x)＞ 0 ∴F(x)在(0,+ ∞ )递增，而F(1)=f(0)-3( 1 −0)-3( 1 −2)=0，∴F(x)＜0的解集为(0,1)，

即f(x−1)＜x2⋅(3−2l nx)+3(1−2x)的解集为（0,1）。

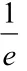
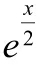
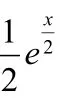
∴F(x)在R上单调递增，且F(2)=e⋅f(2)-1=0，

∴解集为(2,+ ∞)

通过以上实例我们发现利用求导运算法则和利用单调性构造函数有异曲同工之处，我们做出以下总结性的解法足以应对此类题目

（1）解不等式f(x) ＞g(x)，可以直接构造新函数：

F(x)=f(x)-g(x)，之后再对F(x)求导

（2）由x⋅f′(x)+f(x)＞0(＜0)可以直接构造函数：

F(x)=x⋅f(x)，之后再对F(x)求导

（3）由αs i nα_βsinβ，可以利用其结构特征、直接构造新函数F(x)=xsinx，之后再对F(x)求导

（4）由x⋅f′(x)-f(x)，可以直接构造新函数：

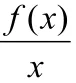
（5）由x2⋅f′(x)-2x⋅f(x)，可以直接构造新函数：

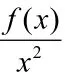
（6）由f′(x)+f(x)＞0，可以直接构造新函数：

F(x)=ex⋅f(x)，之后再对F(x)求导

（7）由f′(x)-f(x)＞0，可以直接构造新函数：

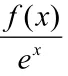
我们将上面的几种结构重新梳理一下，可以发现模型实质为F(x)=f(x)⋅xk,k=−1,1,2。和F(x)=f(x)⋅ek x，k=−1,1，的形式。

（8）对于k f(x)+f′ (x) (kR )的情况：可设函数：

F(x)=ek xf(x)，之后再对F(x)求导。