空间几何体求解中的误区与警示

■王旭泷

对空间几何体的认知,凸显空间问题平面化、模型化和代数化的本质属性。大家在解题中容易出现思维误区,本文结合实例“剖析”之。

误区1：确定三视图时,忽视“投影面和虚实线”

例1 将正方体(如图1)截去两个三棱锥,得到如图2所示的几何体,则该几何体的侧视图为( )。

图2

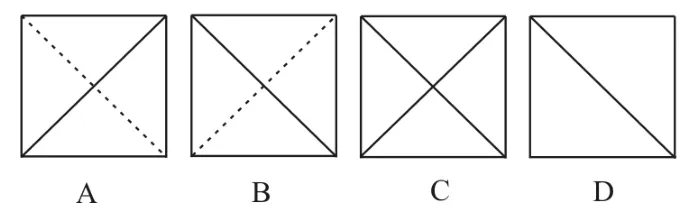
错解：忽视正视,侧视,俯视三个两两垂直方向的正投影,分不清选项A和B,易选A。对三视图画法中的虚实线不明确易选C或D。

剖析：侧视图中能够看到线段AD1,应画为实线,而看不到线段B1C,应画为虚线。由于AD1与B1C不平行,可知投影为相交线。应选B。

警示：在画三视图时,应把握正视,侧视,俯视三个两两垂直方向的最大直截面,要特别注意几何体中与投影面垂直或平行的线及面的位置,认清规定方向上平行投影的实际结果。画三视图时,分界线和可见轮廓线都用实线,被遮住的部分的轮廓线用虚线,要注意“投射光源”的位置是投影面的正对面。

误区2：三视图还原几何体时“虚实不分,对应不当,不作检验”

例2 如图3,网格纸上的小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为_____。

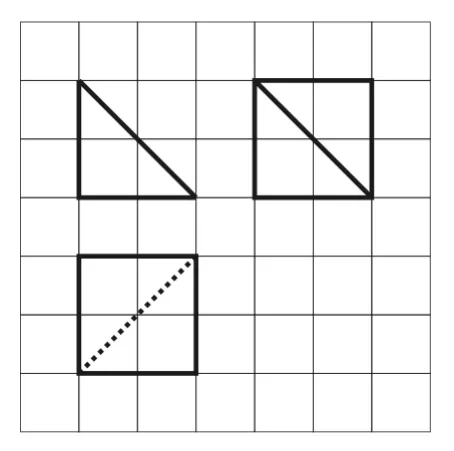
图3

错解：由三视图知,其直观图为四棱锥,四棱锥的底面为正方形,边长为2,四棱锥的高为2,则该棱锥的体积V=。

剖析：还原几何体时缺少模型化的意识。答案对了,但解题过程错误。

根据三视图,可知该几何体是一个棱长为2的正方体去掉一个三棱柱和一个三棱锥后的四棱锥E-ABCD,如图4所示。

图4

该四棱锥E-ABCD的体积V=V正方体-

警示：利用三视图还原直观图时,一定要全面把握几何体的特征,分清三视图中的虚线和实线,最后还应该对还原后的直观图进行检验。

误区3：三棱锥的体积求解中忽略“等积变换”

例3 如图5,在棱长为5的正方体ABCD-A1B1C1D1中,EF是棱AB上的一条线段,且EF=2,Q是A1D1的中点,点P是棱C1D1上的动点,则四面体PQEF的体积( )。

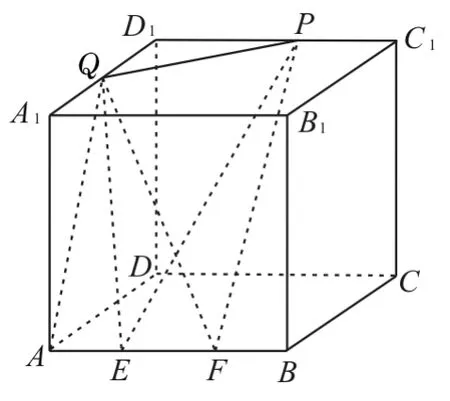
图5

A.是变量且有最小值

B.是变量且有最大值

C.是变量且没有最值

D.是一个不变的量

错解：应选A或B或C。

剖析：忽略三棱锥体积的等积变换易错选A或B。由AB⊥侧面AA1D1D,可知QA为Q点到AB的距离。因为EF=2,所以S△QEF为定值。由C1D1∥AB,可得C1D1∥面QEF,则C1D1到面QEF的距离为定值,而P是棱C1D1上的动点,所以P点到平面QEF的距离也为定值,由此可知四面体PQEF的底面积和高均为定值,可得四面体PQEF的体积为定值。应选D。

警示：求三棱锥的体积的解题关键是寻找易求的底面和对应的高。

误区4：忽略共面的条件和面面平行性质定理的应用

例4 下列正方体或四面体中,P,Q,R,S分别是所在棱的中点,这四个点不共面的一个图是( )。

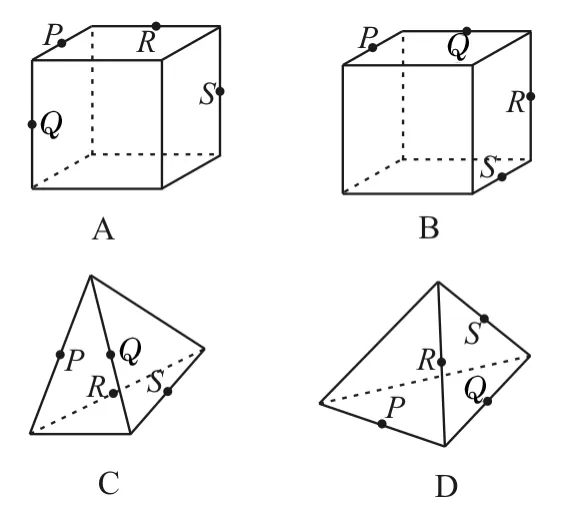
错解：应选B或C。

剖析：错解的原因是不理解共面的条件和面面平行的性质定理。

直接作出截面或用反证法判断。对于A,可作出截面为梯形。对于B,由面面平行的性质定理,可作出截面为正六边形。对于C,空间四边形的四边中点可构成平行四边形。对于D,由反证法或异面直线的判定定理,可知四点构成异面直线,即四点不共面。应选D。

警示：要作两个相交平面的交线,只需找出两个公共点。当平面较小不足以体现交线时,可采用作平行线或作延长线的方法延展平面,直到能作出交线为止。

误区5：盲目类比平面几何中的定理和性质

例5 如图6所示,已知E,F分别是长方体ABCD-A1B1C1D1的棱AA1,CC1上的点,且AE=C1F。求证:四边形BED1F是平行四边形。

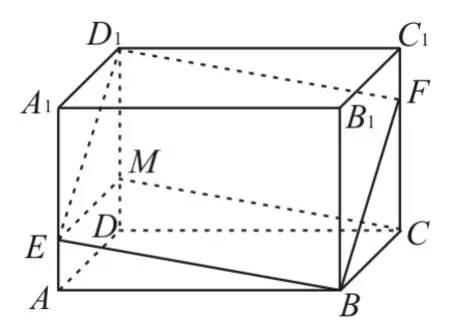
图6

错解：在长方体ABCD-A1B1C1D1中,平面A1ADD1∥平面B1BCC1。由两平行平面与第三平面相交其交线平行,可知D1E∥FB,同理可得D1F∥EB,故四边形EBFD1为平行四边形。

剖析：上述解法盲目套用平面几何定理致错。在DD1上取DM=AE=C1F,连接CM,EM。

由CF=D1M=CC1-C1F,CF∥D1M,可知四边形CMD1F为平行四边形,所以CM∥FD1,CM=FD1。同理可证四边形ADME为平行四边形,所以EM∥BC,EM=BC,可知BCME为平行四边形,可得BE∥CM,CM=BE。

所以BE∥FD1,BE=FD1,可知四边形EBFD1是平行四边形。

警示：平面几何中的有关结论在空间中不一定成立。平面几何的结论在立体几何中的应用遵循两点:①空间中放在同一平面内使用;②先证明在空间是真命题再使用。

误区6：忽视空间中平行与垂直的判定定理的条件

例6 设a,b为两条直线,α,β为两个平面,且a⊄α,a⊄β,则下列结论中不成立的是( )。

A.若b⊂β,a∥b,则a∥β

B.若a⊥β,α⊥β,则a∥α

C.若a⊥b,b⊥α,则a∥α

D.若α⊥β,a⊥β,b∥a,则b∥α

错解：应选A。

剖析：不能准确把握空间中平行与垂直关系的判定定理和性质定理中的条件导致出错。对于A,若b⊂β,a∥b,且a⊄β,则根据线面平行的判定定理可得a∥β,A正确。对于B,若a⊥β,α⊥β,则根据空间线面位置关系可知a⊂α或a∥α,而a⊄α,所以a∥α,B正确。对于C,若a⊥b,b⊥α,则a⊂α或a∥α,而a⊄α,所以a∥α,C正确。对于D,由a⊥β,b∥a,可得b⊥β,因为α⊥β,所以b⊂α或b∥α,可知D错误。应选D。

警示：利用线面平行,线面垂直,面面平行或面面垂直的判定定理时,一定要注意定理的前提条件。

误区7：两直线位置关系的判断中忽略“反证法”的应用

例7 已知m,n为异面直线,m⊂平面α,n⊂平面β,α∩β=l,则直线l( )。

A.与m,n都相交

B.与m,n中至少一条相交

C.与m,n都不相交

D.至多与m,n中的一条相交

错解：应选A。

剖析：忽略题设条件、缺少应用反证法研究问题的意识出错。

假设l与m,n都不相交。由m⊂平面α,n⊂平面β,可知m∥l,n∥l,即m∥n∥l,这与m,n为异面直线矛盾,故假设不成立,即直线l与m,n中至少一条相交。应选B。

警示：简单的空间位置关系的判断问题,可以利用选项和题设条件,通过反证法进行推理判断。

误区8：忽视线线垂直和线面垂直的相互转化

例8 如图7所示,在三棱柱ABCA1B1C1中,点A1在平面ABC内的射影点D在AC上,∠ACB=90°,AC=CC1。

求证:AC1⊥A1B。

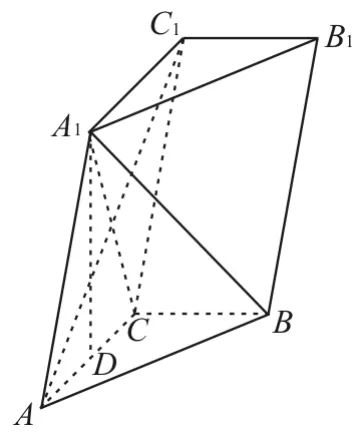
图7

错解：缺少线面垂直转化为线线垂直的意识,导致思维混乱,从而无法证明。

剖析：证明线线垂直,可构造证明一条直线和一个平面垂直。

由A1D⊥平面ABC和面面垂直的判定定理知,平面AA1C1C⊥平面ABC。由BC⊥AC和面面垂直的性质定理知,BC⊥平面AA1C1C,所以AC1⊥BC。由AC=CC1,可知AA1C1C为菱形,所以AC1⊥A1C。

因为A1C∩BC=C,所以AC1⊥平面A1BC。又A1B⊂A1BC,所以AC1⊥A1B。

警示：证明直线与平面垂直、平面与平面垂直,都可借助于直线和直线垂直加以证明。