强非线性梁求解的径向基函数方法

祖福兴， 徐绩青， 李岩汀

(1. 重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074； 2. 重庆交通大学 水利水运工程教育部重点实验室，重庆 400074)

0 引 言

自20世纪40年代以来，求解非线性问题的计算方法一直是非线性科学中的重要课题。由于各种解法对于非线性问题的求解不具有封闭性，致使各方法往往只能对弱非线性问题有效。对于强非线性问题的求解，要么是针对个案问题采取特殊的计算技术来进行，要么是采用近似的追踪方法来进行，因此在理论上没有完备的通用方法。

梁的大挠度弯曲问题属于强非线性问题，且常为四阶微分方程并包含非幂次项，求解难度大，采用通常的有限元方法很难获得令人满意的结果。近年来，国内外学者相继提出了小波分析方法[1]、微分求积法[2]、保辛-保能的数值积分法[3,4]等，这些方法虽然各有优点，但对于多元(多于4个变元，即多维空间的问题)强非线性微分方程，还需要引进某种近似，例如摄动法[5]等。由于这些近似仍会产生一些问题，尚需继续实践探讨[6]。

径向基函数以空间距离为自变量，由于其形式简单、各向同性的优点，近年来得到了很快的发展，并被广泛应用于散乱数据处理、微分方程求解等领域。同时，一种将径向基函数与配点法结合的无网格法[7]也受到了广泛的关注，但这种强格式无网格法通常在边界处容易产生较大的数值震荡。目前，通常采用在边界处加密配点的不均匀配点方案、PDECB方法[8]、调整边界点的权重[9]来减小计算误差。徐绩青等[10]提出了直接应用径向基函数配点法离散时间区域的动力问题求解方法，通过构建适当的插值函数并添加初始条件实现了减小边界处数值震荡的目的。这种方法已成功用于Bratu型强非线性方程[11]和非线性动力系统的数值求解[12]，并取得了不错的求解效果。笔者在此基础上提出一种适用于梁大挠度弯曲问题求解径向基函数逼近思想结合加权余量配点的高精度计算方法。

1 径向基函数法

径向基函数(radial basis function，RBF)是一类以径向距离为自变量的基函数，记为：φ=φ(Rj)，其中，自变量Rj=‖x-xj‖2，为任意点x到节点xj的欧氏距离，且Rj∈Rd。而φ(Rj)在本质上是一个定义在[0，+∞)上的一元函数，其简单的形式为存储和计算带来了很大的优势，这个特点对于多元问题，如：板壳、空间结构，甚至是高维问题，相比其他类型的基函数，例其具有明显的优势。径向基函数插值的收敛性非常好，不仅函数本身有较高的收敛阶，其各阶导数也有很好的收敛速度[13]。

根据作用范围，径向基函数可分为2大类：①全局径向基函数(globally supported RBF)，这类RBF大多是在一定的数学和物理背景下提出的，因此很受欢迎，但它们在计算过程中经常会产生病态稠密矩阵，且应用全局径向基函数的求解精度严重依赖于系数的选取；②紧支撑径向基函数 (compactly supported RBF)[14,15]，它们在计算中通常形成带状稀疏阵。与其他类型的紧支径向基函数相比，由吴宗敏[13,15]教授所构造的局部紧支撑径向基函数，国际上称为Wu函数，是严格正定的。笔者应用Wu函数作为插值基函数，式(1)～式(3)这类径向基函数按照在给定维数空间正定和连续性条件进行选用，具体原则及数学性质见文献[13，15-16]：

(1)

(2)

(3)

式中：r=Rj/Rmax, j(Rmax, j为定义在节点xj处的支撑域半径)；(1-r)+定义为：

1.1 RBF方法基本过程

径向基函数求解的一阶非线性微分方程如式(4)[10,11]：

(4)

将求解区域Ω用n个节点xj(j=1，2，…，n)离散，函数y(x)在区域Ω里的近似解可用一个基本的插值函数表示，如式(5)：

(5)

式中：αj为各离散点的权重系数；α为权重系数向量，α=[α1，α2，…，αn]T；Φ(x)为插值基函数向量，Φ(x)=[Φ1(x)，Φ2(x)，…，Φn(x)]T。

令近似函数yh(x)在各个节点xj处的取值与函数y(x)在相同节点处的真实值yj相等，即yh(xj)=yj，则可以得到n维线性方程组：

Aα=y

(6)

y=[y1,y2,…,yn]T

由式(6)得到权重系数α=A-1y，代入式(5)可得：

yh(x)=ΦT(x)A-1y=N(x)y

(7)

令N(x)=ΦT(x)A-1，由于yh(x)是解析表达式，故可求得一阶导数为

y′(x)=N′(x)y

(8)

式中：N′(x)为时间特征函数(类似于形函数)。

可见，N(x)起到了形函数的作用。

将式(7)、式(8)代入方程(4)，则在求解区域Ω内的原平衡方程，被离散成n个非线性代数方程的方程组(9)：

f(y,N′(x)y)=0

(9)

通常采用迭代算法来求解该非线性方程组，因此，可直接替换或添加边值条件所对应的方程，如将方程组(9)中x=a和x=b对应的第1个和第n个方程替换为y1=a，yn=b，解该方程组即可求得y=[y1，y2，…，yn]T。

但是数值实验显示，这种径向基函数方法的计算结果越靠近边界误差越大，最大误差通常出现在边界附近区域[17]。

1.2 误差改进

针对微分方程(4)构造插值函数如式(10)：

(10)

式(10)相比式(5)增加了边界点上的一阶导数项。同样，将各配点坐标代入式(10)，可得到n维线性方程组，此时系数矩阵A不再是方阵，A-1是对应的广义逆矩阵。按照与式(7)～式(9)同样的步骤，将方程(4)离散为一组非线性代数方程组，并代入边界条件。为了使边界点上不仅满足边界条件同时也满足微分方程，考虑增加一阶导数的边界条件：

该边界条件可由控制方程(5)求解。在离散过程中表达为

求解该n+ 2维的代数方程组可得微分方程的解。

为了克服经典的牛顿法对初始点敏感和收敛性不佳等问题，笔者建议可联合运用高斯-牛顿迭代法[18]和生物遗传算法[19]来求解非线性代数方程组。

2 算法实施

以3.1的算例为例，本文方法在强非线性梁的微分方程边值问题中的算法步骤如下：

1)建立微分方程，如式(11)。

2)确定求解区域Ω和配点距离Δx，以及配点数目n。

3)选择合适的紧支撑正定径向基函数φ(r)：

式中：xj为各配点处的位置；x为任意位置；Rmax, j为各配点的支撑域半径，建议以配点位置为中心，覆盖整个计算区间。

4)根据各配点位置计算n阶特征矩阵A和其逆矩阵B=A-1。

5)任意位置x处的挠度用径向基函数表示：

ωh(x)=ΦT(x)Bω=N(x)ω

求ωh(x)的各阶导数。若为泛函表达式，如3.2的算例，则根据任意位置x处挠度的径向基函数表达式：ωh(x)=N(x)ω，采用高斯-勒让德积分离散原表达式，从而将泛函表达式转化为代数表达式。

6)将配点位置xj处挠度的各阶导数的径向基函数表达式、转化后的泛函表达式和外荷载的值代入微分方程，建立非线性方程组。在此过程中，为了减小数值振荡，取得满意的计算结果，边界点通常还需要增加附加方程，以满足相应的导数边界条件和边界点处的微分方程，带入边界条件和附加的边界条件。

7)求解方程组，得到各配点位置的挠度值。

3 算例分析

3.1 非线性梁的弯曲

求在弯矩

和梁一端作用轴向集中力P=100 N的联合作用下，简支梁的挠曲变形 。简支梁的长度l=1 m，抗弯刚度EI=50 N·m2。若不考虑轴向变形，挠曲微分方程可以写为：

(11)

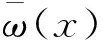
该非线性边值问题(11)有解析解(单位：m)：

可以看出，由于方程(11)中含有非幂次非线性项，难以处理。运用径向基函数配点法进行求解，若采用式(5)作为插值函数，将产生较大的数值振荡。针对问题(11)求解目标是挠度的二阶导数，笔者借鉴弹塑性静力学的处理方法，提出挠度及挠度的二阶变率联合插值的径向基函数表达式：

(12)

为避免式(12)中径向基函数的导数使得系数矩阵条件数增大，应用辅助函数ψ(x)来分别取代式(12)中的二阶导数项，则有

(13)

取Δx=0.1，配点数n=11，φ(x)和ψ(x)分别按式(1)、式(2)计算，其中ψ(x)为辅助径向基函数。代入各配点坐标，按照式(6)、式(7)类似的步骤，可求得形函数

N=

挠度的一阶和二阶变率可分别表示为：

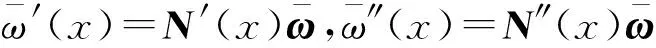
配点法与此相对应，不但要满足微分方程，而且还必须满足简2端边界上挠度、挠度二阶变率的条件，即在边界上也满足微分方程。

算例中，直接调用MATLAB中的fsolve函数(最小二乘法)来求解非线性方程组。计算结果如图1，可以看出数值解与解析解吻合得很好。

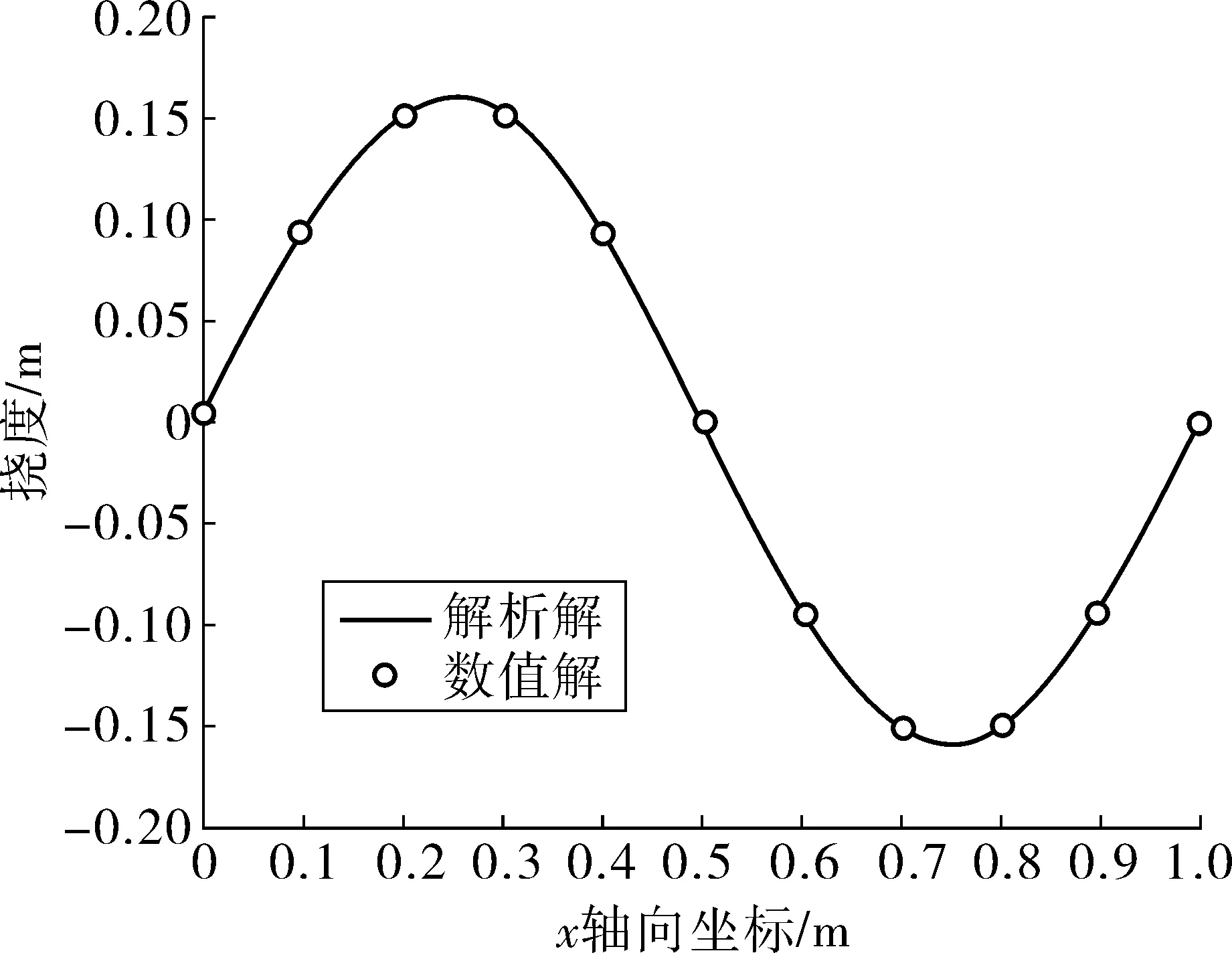
图1 简支弹性几何非线性梁的纵横弯曲Fig. 1 Combined vertical and horizontal bending of simply supported elastic beam with geometrical nonlinearity

表1为笔者提出的方法在配点处的计算值和相对误差。可见，文中方法具有计算过程简单、精度高的特点，其计算精度与修正小波伽辽金法不相上下[20]。

表1 各配点计算结果与相对误差Table 1 Computed results and relative errors of each collocation point

3.2 非线性弹性地基梁的大挠度弯曲

选择一个置于非线性弹性地基上的轴向不可自由伸缩简支弹性梁[20]，梁的长度l=1 m，抗弯刚度EI=1 N·m2，抗拉(压)刚度EA=100 N，地基刚度系数k=100 N/m4，则作用于梁上的横向分布力p(x)(单位：N/m)为：

梁的挠曲线微分方程和边界条件：

做无量纲化处理，梁的挠曲线微分方程及边界条件如方程(14)，此方程含有泛函表达式，增加了求解的难度：

(14)

式中：H、F均为无量纲参数，H=Al2/I，F=kl3/(EI)；P(x)=p(x)l3/(EI)。

将方程(14)中的几何非线性项做近似处理(弱非线性时可行)：

则，此时近似系统的理论解为：

运用径向基函数配点法，取Δx=0.05，均匀配点数n=21。内插2个高斯积分点，采用三点高斯-勒让德积分离散泛函表达式，将泛函表达式化为代数表达式引入非线性方程组。为便于程序实现，高斯积分点既用于数值积分，又用于径向基函数配点计算，总体方案为23个非均匀配点。

为了避免边界出现数值振荡，提出挠度、挠度的二阶变率、挠度的四阶变率联合插值的径向基函数表达式：

(15)

为避免式(15)中径向基函数的高阶导数使得系数矩阵条件数增大，应用辅助函数θ(x)和ψ(x)来分别取代式中的二阶和四阶导数项，则有插值函数(16)：

(16)

式中：θ(x)、ψ(x)、φ(x)分别按式(1)、式(2)、式(3)计算。

由式(16)计算出ω=[ω1，ω2，…，ωn，v1，v2，v3，v4]T(v1、v2、v3、v4为附加未知量，分别为梁的两个边界上挠度的二阶变率和四阶变率)。

配点法与此相对应，不但要满足微分方程，而且还必须满足两端边界上挠度、挠度二阶变率、挠度四阶变率的条件，即在边界上也满足微分方程，附加四阶变率边界条件的约束：ω(4)(0)=ω(4)(1)=0，这样才能很好地消除数值振荡的影响，获得满意的结果。

从图2可以看出，数值解与解析解吻合得很好。

图2 简支非线性弹性地基梁的横向大挠度弯曲Fig. 2 Transverse large deflection bending of simply supported nonlinear elastic foundation beam

图3给出了各配点的相对误差，最大误差为0.67%；本算例用ANSYS软件求解，相对误差高达10%～12%，应用修正小波伽辽金法求解，相对误差也有3%～6%[20]。笔者提出的方法具有计算过程简单、精度高的优越性。

图3 各配点计算结果的相对误差Fig. 3 Relative error of each collocation point

4 结 论

笔者将径向基函数逼近与配点法相结合，提出了对应的插值表达式，构造了一种适用于强非线性梁求解的数值算法。算例分析表明，与传统的数值计算方法相比，笔者提出的方法具有以下优越性：

1)无网格，计算过程简，计算精度高。

2)针对具体的工程问题，配点位置可以根据需要灵活选取均匀或非均匀配点，且在较少配点的情况下也能够获得较高的计算精度，针对非线性问题文中方法具有一定优势。

3)关于径向基函数的选择，紧支柱正定径向基函数相比国外的全局径向基函数，前者的计算结果不依赖于参数的选择，可以根据计算精度和效率的要求设置支撑域半径，更适合在工程实践中推广。