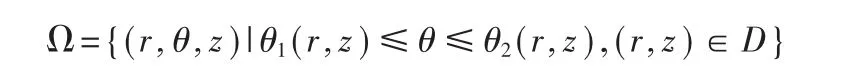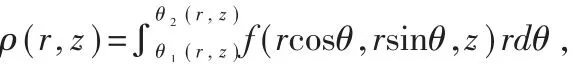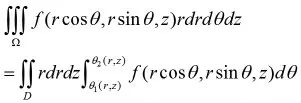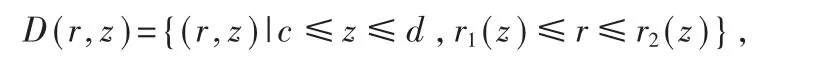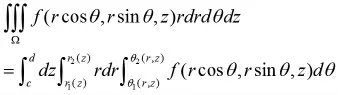在柱面坐标系下三重积分计算法的探讨
邓 进
(湖南工程学院理学院,湖南 湘潭 411104)
0 引言
三重积分的计算是多元积分学中的重要知识章节。 教学过程中,学生往往反映难度很大;困难之处在于将三重积分转化为累次积分时, 无法顺利地确定累次积分的积分上限和积分下限。 一般教材和已有文献多是介绍在直角坐标下三重积分的计算方法中的投影法和截面法,[2]介绍了在柱面坐标下的投影法,即将积分区域投影到极坐标面上的投影法。 但是, 柱面坐标下三重积分的投影法并不完善。 本文给出柱面坐标中的新的投影的概念, 并进一步探讨在柱面坐标下将三重积分转化为三次积分的投影法。
1 柱面坐标系[1,2]
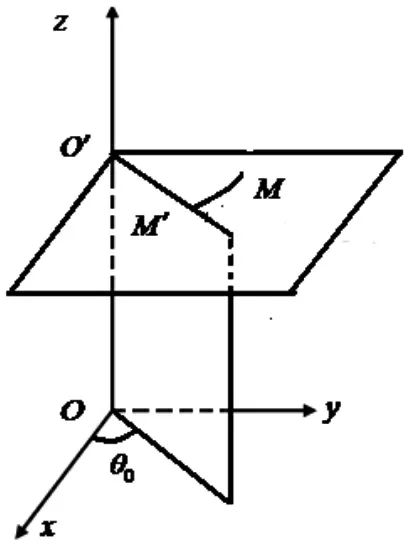
设M(x,y,z) 为空间内一点,并且设点M 在坐标面xOy 上的投影M'的极坐标为(r,θ),则有序三元数组(r,θ,z)就叫做点M 的柱面坐标(如图1 所示)。
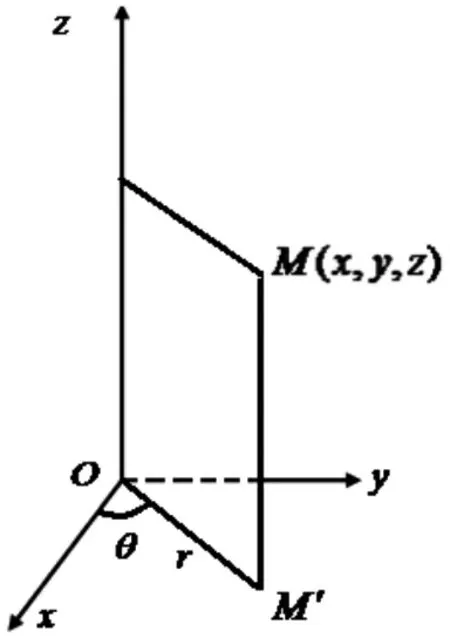
图1 柱面坐标系
这里规定r,θ,z 的变化范围分别为:
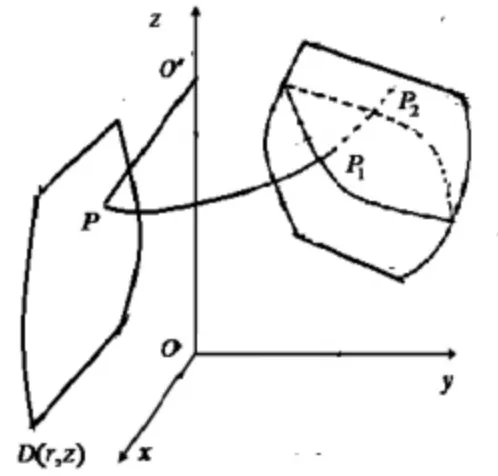
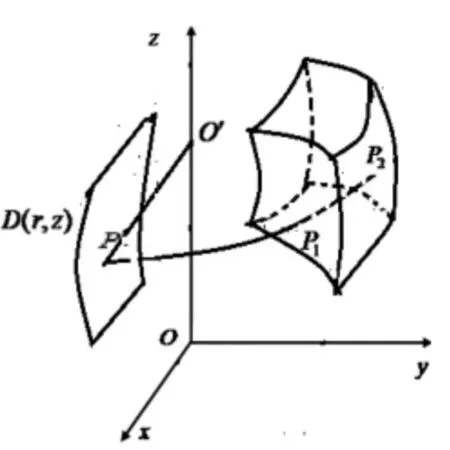
0 ≤r<+∞,0 ≤2π,-∞ 由图1 可知,点M 的直角坐标(x,y,z)和柱面坐标(r,θ,z)的关系为: x=rcosθ,y=rsinθ,z=z 柱面坐标系中的三个坐标面分别为: r 为常数:以z 轴为中心轴的圆柱面; θ 为常数:过z 轴的半平面; z 为常数:与xOy 面平行的平面. 不难知道, 柱面坐标下三重积分的体积微元dv=rdrdθdz,因此利用可得柱面坐标下三重积分的形式为: [2]中详细介绍了柱面坐标下三重积分的投影法,即将积分区域投影到极坐标面并进一步将三重积分转化为三次积分。 下面介绍一种新的投影法。 ②石孝友《卜算子》(见也如何暮):双调44字,上阕4句3仄韵,下阕4句3仄韵。句式:5575。5575。 图2 在半平面内的投影示意图 定义1 设θ=θ0为固定的半平面,过点M 作垂直于z轴的平面,该平面与z 轴的交点为O',在该平面内以O'为 圆 心, 以|O'M|为 半 径 作 圆 交 半 平 面θ=θ0于 点M',称点M'为点M 在半平面内θ=θ0的投影(如图2 所示)。 将空间区域Ω 内任一点均投影到半平面θ=θ0上,得到空间区域Ω 在半平面θ=θ0上的投影区域D。 一般而言,选取θ=0 为所需的固定半平面。 此 时, 区 域Ω 的 边 界 面 上 有 两 个 曲 面θ=θ1(r,z),θ=θ2(r,z)此外,还有可能有一部分是以为中心轴,由投影区域D 的边界曲线绕轴旋转而得到的旋转曲面的一部分。 如图3 和图4 所示的两种情况。 图3 区域Ω 的边界面(情形1) 图4 区域Ω 的边界面(情形2) 因此, 空间立体Ω 的质量可以看作密度不均匀的平面薄片D(r,z)的质量,只需要求出面密度ρ(r,z)即可。 而对区域D(r,z)内的任一点(r,z), 从而 因此, 进一步,可将外层的二重积分转化为二次积分。 如果投影区域D(r,z)表示为 则 从而,把三重积分转化为先对θ,再对z,最后对r的三次积分。 如果投影区域D(r,z)表示为 则 从而,把三重积分转化为先对θ,再对r,最后对z的三次积分。 特别地,如果积分区域为: Ω={(r,θ,z)|α ≤θ ≤β,α ≤r ≤b,c ≤z ≤d} 则三重积分可转化为: 综上所述, 柱面坐标下三重积分的投影法可以总结为一句口诀,即“一投二交三积分”。 在上面公式的推导中, 假定了垂直于z 轴的平面内任意以z 轴和该平面的交点为圆心的圆弧与空间区域Ω 的边界曲面相交于不超过两点(位于Ω 的边界上的圆弧除外)。 实际上,对于更一般的情况以上公式同样成立, 只需要将分为若干个满足上述条件的区域的和, 然后利用三重积分关于积分区域的可加性计算即可。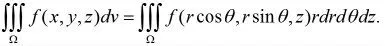
2 投影法