深远空连续推进动力与施图林格解的解析

栾恩杰

（国家国防科技工业局，北京 100048 ）

我在有关的文章中曾经提过将深空探测的动力系统作为一个独立分支进行研究的意见。此文在讨论有关的问题时，将采用国际宇航科学院（International Academy of Astronautics，IAA）的“星际科学先导任务项目（Interstellar Precursor Mission，IPM）”[1]的有关内容。因为我觉得“IPM”所涉及的概念相当丰富，对我们的深空探测活动具有很重要的启示。

1 深远空探测任务的推进动力应作为空间动力的一个独立的门类

在确定“深远空”（Very Far，VF，或者称其为远深空）天界时，最近有一些报道将太阳风层顶（100 AU）以外的空间环境作为星际太空的起端（Heliopause）。并以此表述为飞出太阳系的边缘。我认为在确立太阳系的边缘处时，可以延续在太阳系中太阳—地球、地球—月球间及行星间影响球的概念，比如在地球表面的物体受到地球的引力比太阳对其的引力要大1 600多倍，实际上在距离10倍地球半径时，其引力只有地球表面的1%。也即处于影响球之内时，只考虑一个主天体的作用，不会影响我们的分析和判断。按这个意见，我们太阳系与比邻星系则是两个相距约2.7×105AU的主天体，在研究我们太阳系的行星运动时，并不必要加入比邻星的作用，从这个意义上说是否可以按影响球概念定义太阳系的天界。简单而言之，如果比邻星的质量与太阳系相同，，其影响球处于2.7×105AU，其一半的距离也在10万AU，所以有学者认为太阳系的边缘在10万AU以上，即使有50 km/s的飞船，飞到这个距离也要1 200多年（），如果我们以这个目标作为现在的人类要实现的目标的话，由于其距离太过遥远，所需行进时间太过漫长，将使我们望而却步，起不到任何激励作用，在太阳系远深距离（very far space destination）的定义中将科学目标和技术目标综合考虑，将技术型任务和科学型任务结合起来判断。IAA的IPM将太阳系的边界设定在80～100 AU处，也是有一定道理的。在未来先进的深空动力系统得以实现突破，使飞行器飞行速度达到100 km/s以上时，实现500 AU距离的任务也是具有实践推动性和未来挑战性的。

在深远空的行动中，人类将面临诸多从未遇到过的，或者说很少思索的问题。

首当其冲是深远空推进动力问题，它和超远的飞行距离紧密相关。化学推进剂的极限能量是mc2，所以单位质量的极限能量为(3×105×103m/s)2=9×1016J/kg，目前可能达到的单位质量提供的能量在(0.8～1.25)×107J/kg水平，它的喷射速度ve在4～5 km/s左右。这对超远距离飞行任务所需的时间而言，将是难以承受的，若在三级Mp/M0=0.9的条件下，其终速uτ=3×5×ln(1/0.1)，即34.5 km/s，以这个速度漫游到太阳风层顶（100 AU）处也需13.8年，若要到太阳引力透镜焦点（500 AU ）则需70年。到达奥尔特云104AU处则要1 380年。如果想在20年内达到500 AU，那航天器飞行速度要达到120 km/s。

若在近地轨道处逃离地球引力，其速度增量是第二宇宙速度与第一宇宙速度之差（VII-VI），即12～8 km/s，∆V=4 km/s。它是化学推进剂的喷射速度能够达到的。

怎样才能既加快飞行速度，且能消耗更少的质量呢？显然不能利用火箭的短时间加速（有的书称为脉冲加速）、以霍曼轨道方式奔向目标，所以IAA的IPM所重点关注的是采用稳定、长时间工作的高比冲推力系统，使其达到足够大的速度增量，以便使任务在可以接受的时间内完成。这种稳定、长时间工作的高比冲推力系统，即是我们要重视开发的深空远程的推力系统。

从目前掌握的技术来看，有两种推进系统得到了广泛重点关注。一个是通过太阳辐射直接驱动的太阳帆推进，这是一种利用航天器所处位置的太空资源，称为原位资源（Insitu Resource）。这类资源中的主恒星辐射因其与距离的平方呈衰减而变小，但在更远的将来能否实现星际冲压喷气发动机（Interstellar Ramjet），以就地获取星际质子（H+），目前仍是一种科幻。另一个是电推进（Electric Thrusters，ET），以采集主恒星光能的光伏电池或航天器自带的核电反应堆（Nuclear Electric Propulsion，NEP）作为推力的动力，电推进的比冲比化学推进要高得多，目前我们已经做到高于液体火箭发动机（LRE）的10倍以上，其喷射速度（vc）达到40 km/s。

在IAA的“IPM”一书中第4章提到用电力实现太空旅行的概念可能是由施图林格在二战期间提出来的（Possibly the first suggestion to apply electric power to space travel was by Stuhlinger during WWⅡ.）。在书中的参考文献中，只引用了一篇施图林格（Stuhlinger）的文章，是1964年的《太空飞行的离子推进》[2]他所以提出电推力主要原因是这种推力系统可以获得比化学能高得多的比冲，他认为核电可以为其提供动力源。

如果说爱因斯坦的质—能关系表示小质量转化成巨能量，那么利用电推进就是以高喷射速度得到小质量下的大比冲。

2 施图林格解的解析

施图林格给出了一个连续常值推力的方法，也即飞行器所受到的推力不是常规化学推进剂的短时间加速过程，关机后它将按圆锥曲线轨道运行。用我们习惯的说法，深远空常值推进系统是长时间处于主动段飞行的飞行器。正是在这个设定下，施图林格开发了加速度（速度增量）为常值条件下的方法。有关加速度为常值情况的全面分析，还有待进一步研究，所以它只是一个原始的方法。

IAA的IPM给出了这个解的结论。我这里的主要内容是将书中没有表征的过程和推演过程中涉及的一些概念和方法做一个解析，解析过程中是否存在不准确之处，还请有关学者指正。

2.1 施图林格方法的原始出发点是齐奥尔科夫斯基定律。

式中的符号采用IPM文章的写法：uτ为时间τ时的航天器速度，v为航天器推进系统的排气速度，M0为航天器总质量，也即

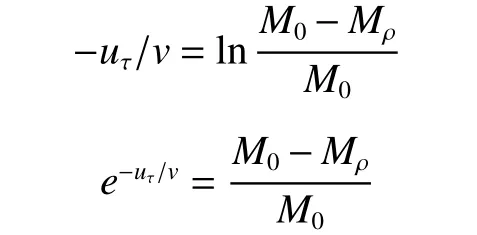
若令M0=Mρ+Mw+ML， 其中Mρ为推进剂质量，Mw为推进系统的干重（不计推进剂系统质量），ML为有效载荷质量（是任务需要的有效部分），

有Mρ=M0-(Mw+ML)，

代入式（1）则

施图林格解表征的是任务的“有效载荷”比ML/M0，所以我们要将Mw表征为与M0有关的方式。为此定义了推力系统的“功率密度”概念。α为功率密度。

令α≡(功率P)/Mw，

理想状态下，推进系统的喷出速度v等于其比冲（Isp），比冲单位为“推力/单位时间消耗推进剂的质量”，m/s。

在α的定义中，功率P应是推进系统在恒定加速度下所贡献的能量。如果我们是在τ时间内稳定地以v速喷出Mρ的推进剂，则其功率P为

所以，α的定义表达式为

将式（3）代入Mρ=M0-(Mw+ML)式中

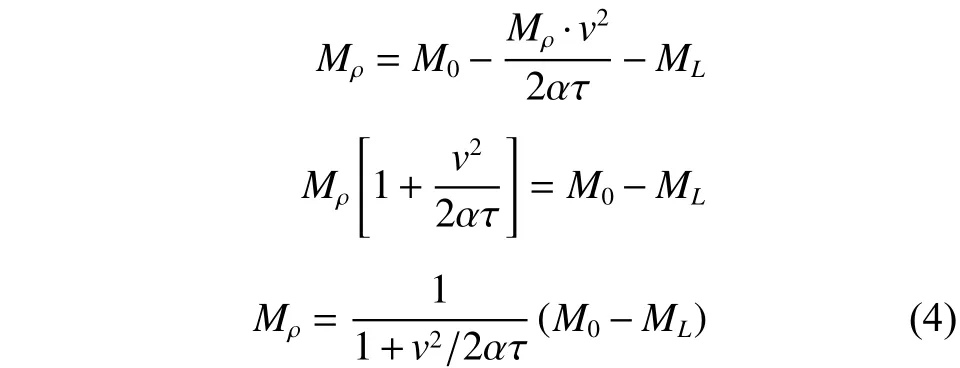
将其代入式（1），有

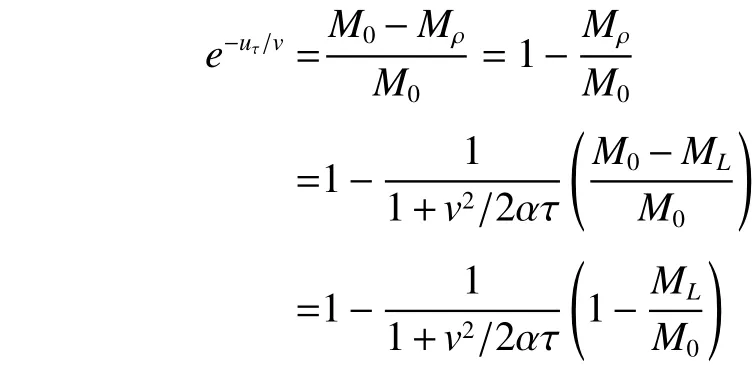
有

此式即称为施图林格解（Stuhlinger's Salution）。

下面讨论一下这个解：

1）施图格林解给出的是有效载荷比ML/M0与最终速度uτ、喷出速度v及推进剂工作时间τ和推进系统功率密度α这四个参数的关系。

2）它的分析基础是齐奥尔科夫斯基定律，从此定律出发，可以推演出我们工程所需的各参数之间的关系与规律。这个解的核心思路是独立出一个“功率密度α”的参数。

3）在下面的解析里，将根据不同的需要形成ML/M0，uτ，τ，及功率P之间的关系表达式。

2.2 距离增量Sτ的精确表达式

在IPM任务中，有关内容反映在4.4节，题目是通用“精确”解（General ‘Exact'Solution）。这里将从前面导出的施图林格解出发，由速度增量∆uτ，导出距离增量Sτ。

仍然假定推进剂喷射速度v是平稳的常值（也即比冲不变），且推进剂的秒耗量也是平稳的。那么推进剂在t时刻的消耗量为

将它代入式（1），有

即

此处的目的是求解Sτ和ML/M0的关系，则应将Sτ的表达式中Mρ/M0转化成ML/M0。为此仍需用到施图林格解的参数定义。将式（4）代入式（6）有

有

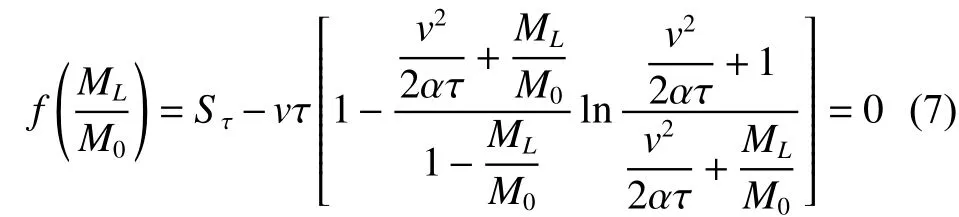
2.2.1 小 结

2）功率密度α值随不同的推进系统而有很大的变化，施图林格主要是针对核电推进作为背景，对核电推进而言，它可能达到（MW/kg）级，如果在一年的任务中2ατ可以达到1013量级，即

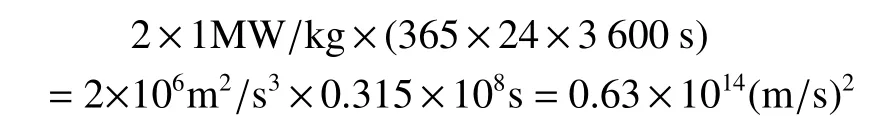
vc达 到107m/s量级。

在这样的vc下 ，除非v（比冲Isp）与其相近，否则式（5）的第二项是可以忽略的，也即式（5）变成

式（8）即为所有化学推进系统的情况，也即式（8）是式（5）的收敛值。

实际上，在α值的定义中，只是推进系统本身的结构质量Mw比值，如果将所有非有效载荷部分的质量一并考虑在Mw里时α值还是较小的。据IPM任务描述，核电推进系统α值的保守估计约为0.01～0.02 kw/kg（即为10～20 m2/s3）。美国国家航空航天局（NASA）使用太阳能电池板驱动的太阳能技术的验证试用发动机（NSTAR）的α=0.17～0.25 m2/s3。

3）对式（5）进行归一化处理，并将uτ和作为参数。表达ML/M0与比冲的关系:

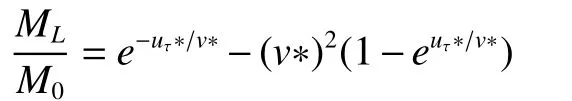
2.3 施图林格解的应用

在IPM任务中，将有效载荷比ML/M0、最终速度uτ、比冲v（Isp）、推进系统任务时间τ、发动机特征速度vc、功率P及功率密度、深远空目标距离Sτ作为研究分析的关键参数，并分析其相应的规律，我认为弄清楚这些概念是非常重要的。在这个领域，美、苏（俄）自1950年代以来，积累了大量的研究成果。而弄清楚这些参数之间的关系，则是这些知识的重要部分。

在上述七个参数之中，特征速度vc与α和τ相关，而α又与P相关。所以在f(ML/M0)=0的“精确”解里，只含有Sτ，v，τ，α及ML/M0这5个物理量。为描述其中2个量之间的关系，必须将其它的3个变量作为参数（Parameter），在这3个参数取值的条件下，得到所需研究的其它两个变量之关系。

在IPM任务中，将Sτ=73 AU 及520 AU ；α=0.1及0.4；τ=5～28年；作为参数，求出ML/M0与v(Isp)之间的变化规律。

f(ML/M0)=0是非线性的方程，可通过迭代方式求解，我将这一过程中的概念说明如下：

首先，将(Sτ-vτ)从方程中移出，然后用vτ除两边得到

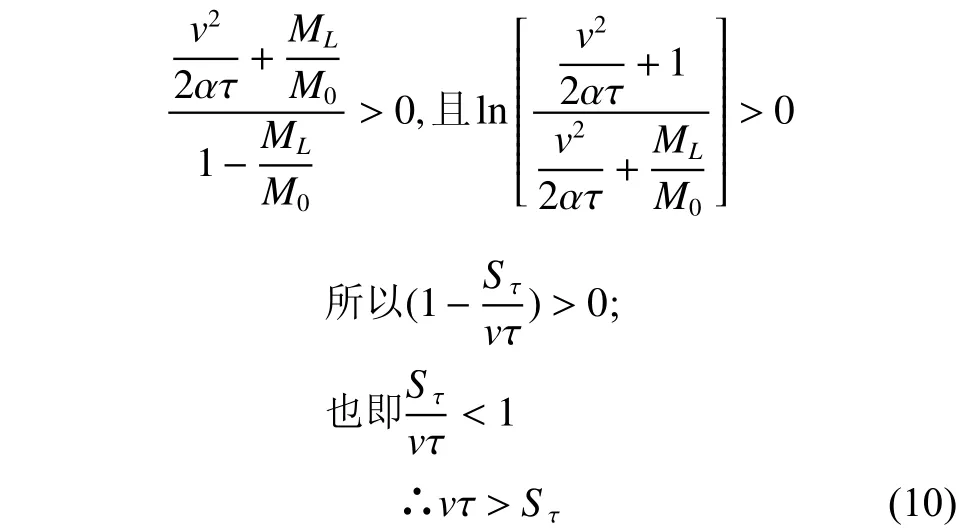
这是任务距离、任务时间及发动机比冲的边际条件，如果出现vτ≤Sτ，则表明发动机以v的比冲在任务要求的时间τ内到达不了Sτ的距离，也即其载荷比已经不可能存在。从表达式中也可看出，是不会小于零的，只有对数项内为1时，也即时才有的情况。据此，我们可以称（）为任务能力被截止的极点（定义为截比J）。而定义为特征值。

例如：求在Sτ=73 AU ，τ=8年的任务要求时，设α=0.1 kw/kg，比冲v=100 km/s的载荷比ML/M0。

首先计算截比值

有了截比J=0.565，则可以迭代求解

式中

则

代入上式

经迭代有ML/M0=0.22时左式值为0.564，误差值在0.001位上可以接受这个结果。

1）当比冲为150 km/s时

说明从v=100 km/s提高到v=150 km/s时，ML/M0是上升的。

说明从v=150 km/s到v=250 km/s ，ML/M0没有提升。在此段比冲的影响不大。

3）再取v=300 km/s时

说明从v=250 km/s 到v=300 km/s ，ML/M0是下降的。

它表明在v=150 km/s到v=250 km/s之间有一个ML/M0的极值点。

4）如果我们取v=200 km/s时

可以从这个例子中看到在8年左右的旅行时间情况下，确实存在一个比冲值，使达到最大。

动力飞行时间τ和比冲v是特征值的关键参数，在τ比较小（比如几年）时，α值比较重要，也即发动机的功率密度影响比较大。如果τ比较大（比如20年），则α值的重要性就低得多。我们可以通过两个例子说明这个结果。

若令τ=8年、Sτ=73 AU 、v=500 km/s， α1=0.1和α2=0.2两个值时的ML/M0来比较。

此时的特征值

可以看出在τ=8年，时间比较短的条件下，从0.1变化到0.2时，ML/M0从0.035变化到0.43达到12倍。影响是很大的，α对载荷比的作用很大。

若令τ=20年、Sτ仍为73 AU 、v=500 km/s，α1=0.1和α2=0.2时的两个值时的ML/M0来比较，此时的特征值为

看出在τ = 20年时，α从0.1变化到0.2时，ML/M0从0.8变化到0.865，只变化约8%左右。

所以α的作用在任务时间长的时候，其重要性降低。

2.4 关于任务时间

对于深远距离的任务，只有采用新型的推进系统，否则难以在可以接受的时间内完成任务。这个可接受的时间“IPM任务”中称为“人的平均工作年限”（Mean Human Job Time，MHJT）。这个可接受是指一个人，而不是一个团队，从确定任务到完成任务（接收到第一批数据）的时间超出了领导这个项目主要专家的工作年龄，认为是不可接受的，一般可以按20～30年以内为好。

下面分析任务时间与α值和v的关系对深远空任务的影响，我们以Sτ为73 AU 到730 AU作为例子来研究。

在有载人的深远空任务中，必须要有较大的载荷比，为此目的，必须有比冲更高的推进系统。

以Sτ=73 AU、v=50 km/s为例，分析任务时间τ与功率密度α的关系。

此时施图林格解表达式为

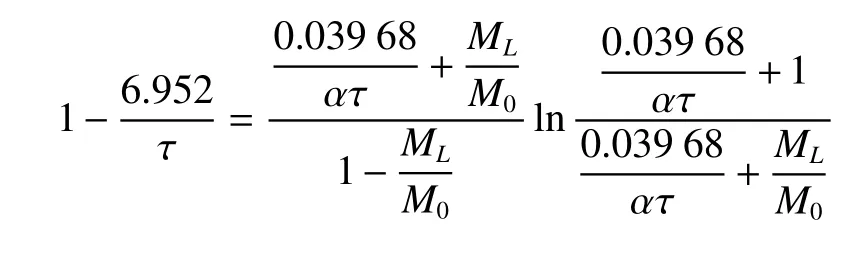
令上式的ML/M0为任务需求，作为参数确定并取0.1值来分析。

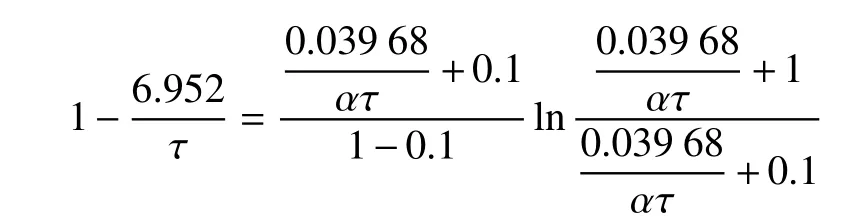
将ML/M0=0.1代入上式式中只含α和τ两个量，以为变量（量纲为kw/kg）迭代求解

在v=50 km/s时，因其比冲比较小，所以特征值L也比较小，为

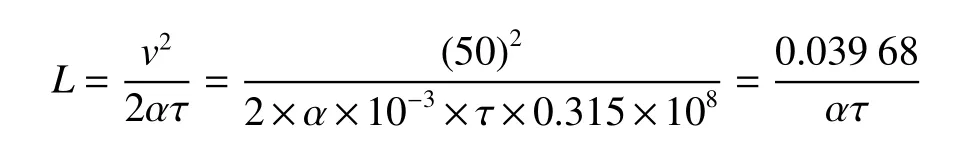
从α=1～α=104，其L从。

而τ往往是10年左右，则L值在4×10-3～4×10-7，所以，在α＞1时L趋于极小量时特征表达式取饱和值E

即当ML/M0=0.1时，其E的饱和值为0.255 8。

由J=E，知亦近似为常值，

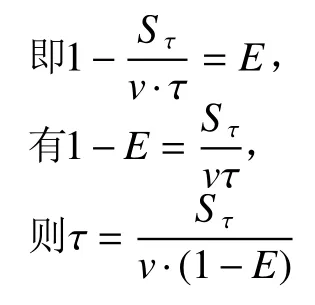
τ的单位是“s”，的单位为“km”，则（年）vτ

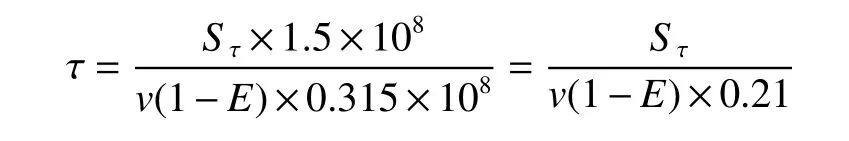
ML/M0=0.1，v=50 km/s，α从1～104的范围内Sτ与τ的对应关系，是将E=0.255 8代入，（年），也即Sτ与τ是线性关系，这就是因为此时特征值L趋于极小。

相应有

即在v=50 km/s，Sτ、ML/M0确定的情况下工作时间τ与α的相关性减弱，几乎是一条直线。的相关性极大。

这是在v=50 km/s下的情况，如果比冲增加到350km/s时，情况是不一样的，我们来讨论这个情况。

当v=350 km/s时，令ML/M0仍为0.1，Sτ仍为参数，设Sτ为730 AU （其规律与73 AU时相同），求任务时间τ与功率密度α的关系。α量纲为kw/kg。

此时截比

特征值

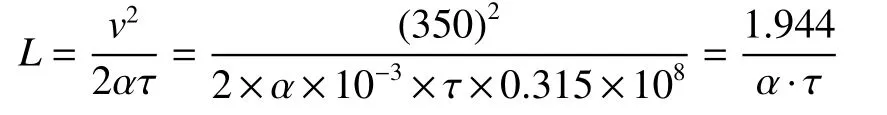
施图林格解表达式为

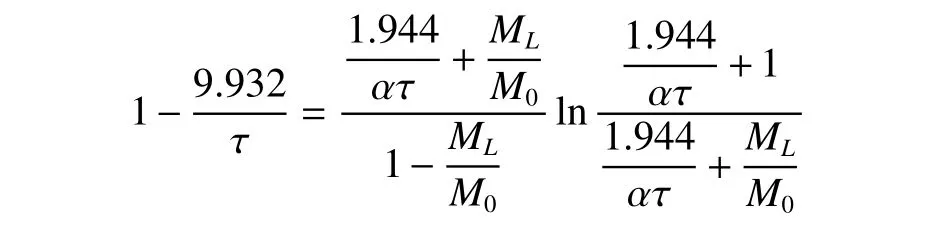
令ML/M0的任务需求为0.1时，上式为

式中只含α和τ两个量，以α为变量迭代求解τ。

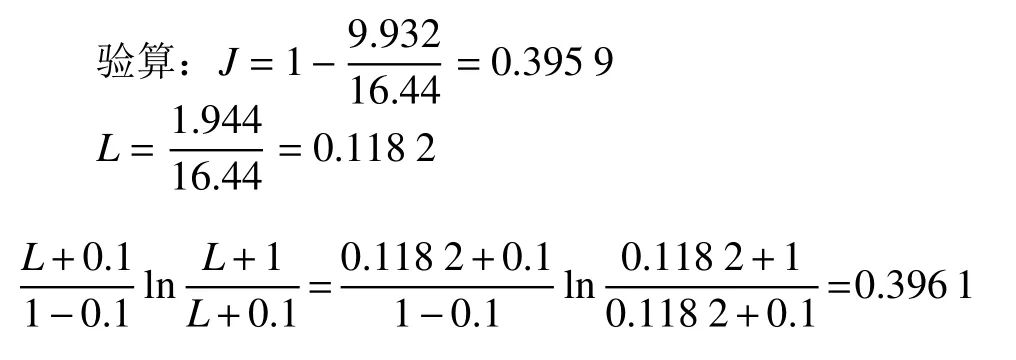
表明当α从0.1变化到1时，τ从29.3年降到16.44年。

当α=10时，迭代有τ=13.73年，

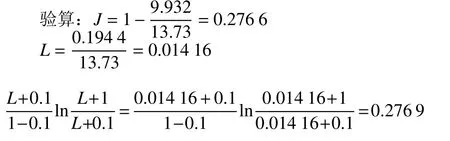
当α=100时，经迭代得τ=13.346年

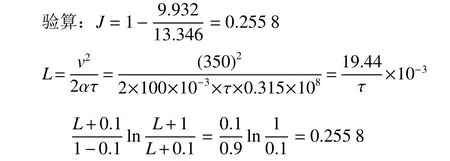
也即τ=13.35年。即是我们前面得到的结果，当L≈0时，E为饱和值0.255 8。

所以其曲线是饱和的，但这个饱和值是在α＞100时。

上述解析过程说明，当比冲Isp较小时（如 50 km/s），任务时间τ与功率密度α的关系不大，几乎是饱和的水平线。它与有效载荷比及任务距离相关。当比冲Isp比较大时（如350 km/s），在α＜1的情况下，τ随着α的增加而下降；在α＞1的情况下，τ与α的提高无甚大影响，也是一个饱和线。

2.5 关于推力系统的功率与比冲

从式（6）出发

在实际的系统中，ML/M0＜1是必然的，前面已经交待过，且，即，这也是必然的。

在研究功率P与比冲v的关系时，将初始质量M0作为参数，因功率，

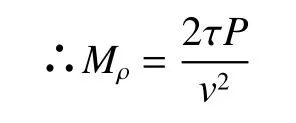
代入式（6）中，

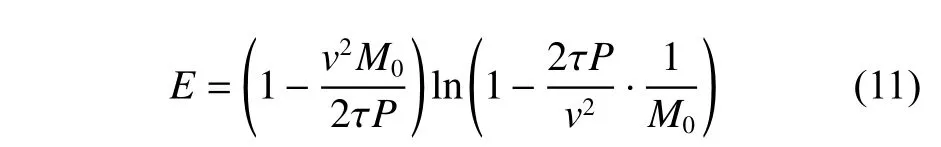
（可称Q为特征参数，无量纲）

由J=E可以迭代求出Q，而特征参数Q里包含有功率P和比冲v，也即在τ和M0为参数条件下可以得到功率P与比冲v(Isp)的关系。

以Sτ=73 AU、τ=20年、M0=10 kg的任务作为一个例子来求解功率P与比冲v的关系。

首先求截比

（v的单位为km/s）

以v=500、300、150、50四点为变量求解其相应的功率值

则当M0=10 kg，τ=20年时有

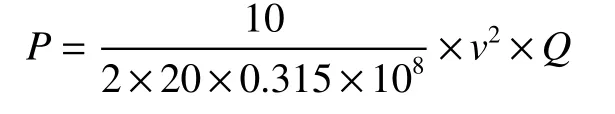
将

代入，且以m/s为单位。则

v(500 km)2=(500)2×106m/s

有

当M0变化时，因各参数皆没变化，所以功率P与M0成正比增加。

若Sτ仍为73 AU， τ为8年时，

其截比

（v以km/s为单位）

仍将M0作为参数，计算P与v的关系。

令M0值为10 kg时

截比J=

将v=500、300、150及50 km/s代入，有

表1Table 1 The relationship between the intercept ratio J and the specific impulse v

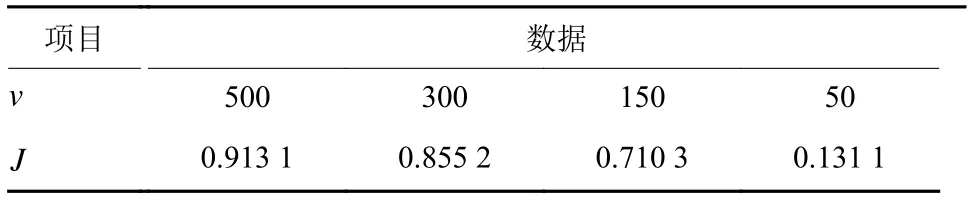
表1Table 1 The relationship between the intercept ratio J and the specific impulse v

?vJ 项目0.59 01 0 3 10.38 05 0 5 2数据0.17 51 0 0 30.1 530 1 1

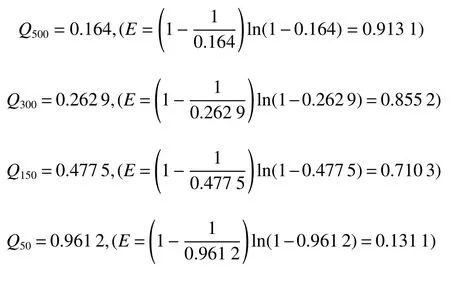
由式（11）

（此处v以m/s 为单位：计算P时v以m/s单位计算，即为(v×103)2=v2×106，所以P的单位是（w））

同样由于P与M0成正比关系，所以随M0的增加，P呈等比上升的趋势。

下面讨论一下Sτ为540 AU 、τ为24年时的情况（M0仍为10 kg）：

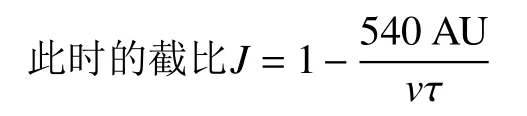
在τ=24年的任务要求时

说明在比冲小于107 km/s，是无法到达任务距离的。所以在小于100 km/s以下，不应有数据，也即这样的条件下在24年内是达不到的。

我们以τ=24年，M0=10 kg为参数，v仍取500、300、150及50 km/s为变量，此时的截比

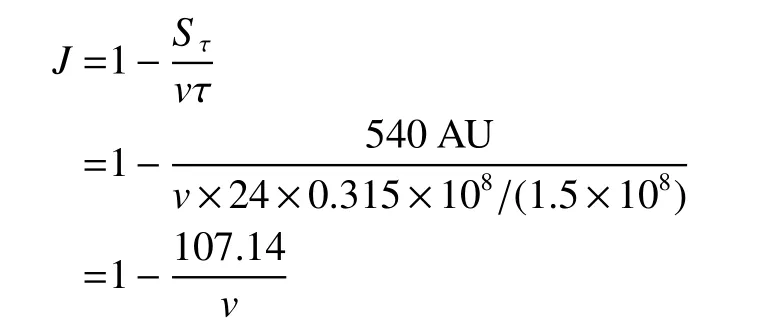
（此处v以km/s为单位）

则有

出现J50＜0，不在任务可行范畴（截比小于0，任务被截止）。

（此处v以m/s为 单位，即v2表示为(v×103)2=v2×106）

有

同理它随M0的增加量比例提高。

2.6 关于最终速度uτ与比冲的关系。

由式（5）可得

可知

这里面含有v、ML/M0、α、τ和uτ这5个变量，此处要求的是uτ与v之间的关系。

为此我们将α、τ作为参数，而将其Sτ、α、τ条件下的ML/M0作为中间待求量，则可得到在这些约束下的最终速度uτ与比冲v(Isp)的关系。

在这个例子中，特征值为

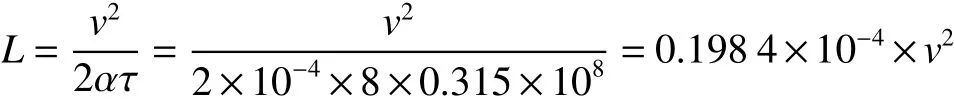
在Sτ任务距离要求下，由式（9）可以求出对应的ML/M0。

当v=150 km/s时

由式（9）对应的ML/M0=0.31，代入式（14），得uτ=-150[ln(0.446 4+0.31)-ln(1+0.446 4)]=97.2 km/s，同样的过程可得表2数据。

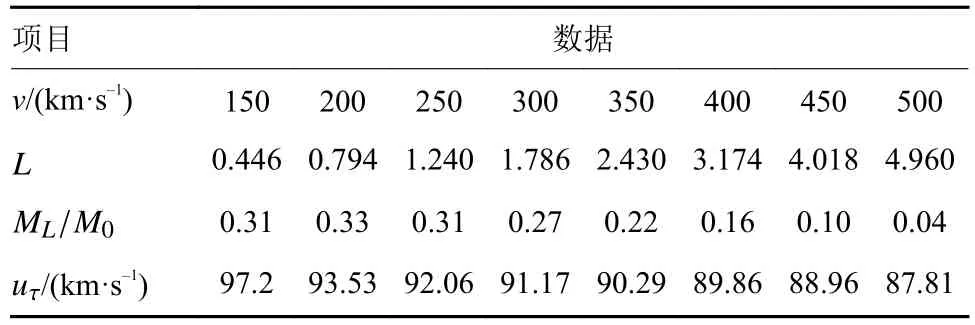
表2 式(14)中的UτTable 2 Uτ in formula (14)

由v=150 km/s到v=500 km/s比冲下的Sτ=73 AU、τ=8年、α=0.1 kw/kg约束的最终速度uτ曲线可参考文献[1]中的图4-3。我们从看到，当v从50 km/s到100 km/s增加时，J从0.131变到0.566，变化幅度为0.44左右，但从200 km/s增加到500 km/s时，J从0.782变到0.913，其变化幅值仅为0.13，所以uτ在大于200 km/s之后变化幅值较慢，几乎是一条直线。

再以τ=28年为例，Sτ仍为73 AU、 α仍为0.1 kw/kg，这时的特征值

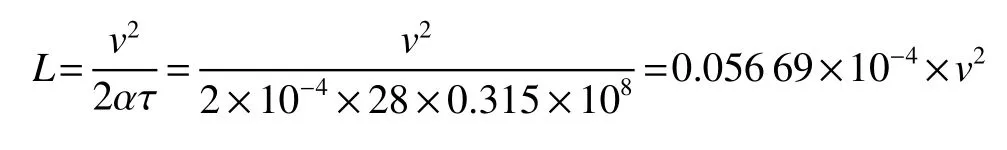
当v=50 km/s时

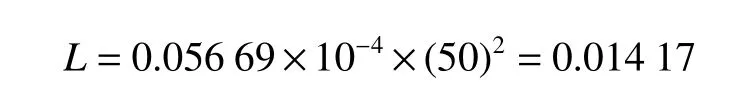
由式（9）对应的ML/M0=0.58，代入式（14），

得uτ=-50[ln(0.014 17+0.58)-ln(1+0.014 17)]=26.73 km/s，按同样的过程得到表3。

表3 式(14)中UτTable 3 Uτ in formula (14)

这个从50 km/s到500 km/s比冲下的Sτ=73 AU、τ=28年、α=0.1 kw/kg约束的最终速度uτ与v(Isp)的关系即为参考文献1中的图4-3的τ=28年的曲线。

这个最终速度的求解问题在齐奥尔科夫斯基公式中已经完整表达，这里只是经过施图林格对其中推进系统装置的功率密度定义后将变形为关于有效载荷比的施图林格解的形式。

2.7 有关有效载荷比的归一化解

为了绘制一个统一的图，将uτ和v都用特征速度进行归一化处理，即，这种归一化处理，并不改变ML/M0的值。

以v∗为横坐标、以u∗为参数、以载荷比ML/M0为纵坐标，得到归一化的表达式。

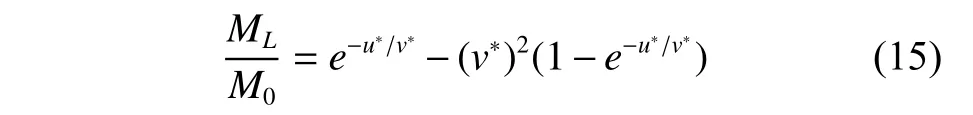
选取v∗为0.01、0.02、0.05、0.2、1和10这6个点及u∗=0.01、0.02、0.05、0.1的值求解ML/M0：

可以看出当v∗=1时ML/M0比和v∗=0.2都要大，也即当比冲v∗接近特征速度时，其载荷比近为极大值。

按同样的过程，求得u∗=0.02的载荷比的变化情况，见表4。

表4 式(15)中ML/M0Table 4 ML/M0 in formula (15)

也表明v∗1时ML/M0出现极大值。

下面讨论当ML/M0趋于极小情况下的u∗、v∗关系。

因ML/M0取值在（1，0）之间，即不可能没有有效载荷，也不可能全部都是有效载荷，即0＜ML/M0＜1。

为了绘制ML/M0与v∗的关系图，我们可以将小于0.04作为ML/M0的最小边值来考虑。

当u∗=0.05，v∗=0.015时

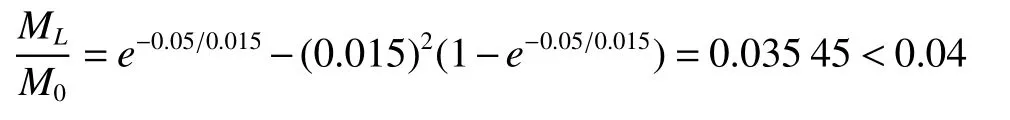
同样可求u∗为各值下v∗值见表5。

在v∗＞1时，其ML/M0取下降趋势，在这一段ML/M0＜0.04时的u∗、v∗的对应关系计算如下当u∗=0.1，v∗=9.9时

同样可得到v∗＞1情况下的相应u∗见表6。

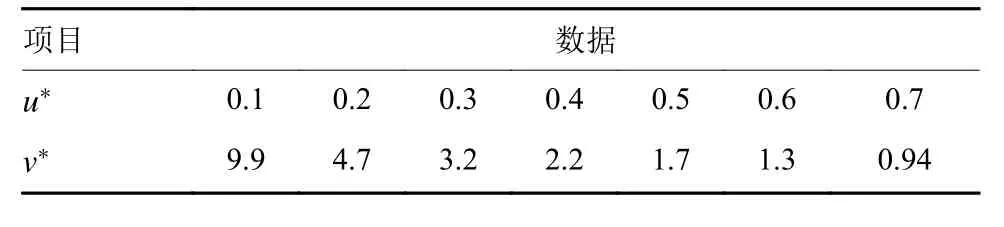
表6 式(15)，ML/M0 ＜ 0.04、u＊ ＞ 1时，u＊与v＊关系Table 6 The relationship between u＊ and v＊， when ML/M0 ＜0.04, u＊ ＞ 1 in formula (15)

我们这样一个点一个点的求取，就是为了说明ML/M0存在一个极值点，在v∗=1的两旁有两个使ML/M0近似趋向于零的v∗值。

对于ML/M0在每个u条件下都有一个v使其达到最大值，而这个v近似等于发动机的特征速度也即当比冲vvc时其载荷比为最大值。这在上述的演算中得到了说明。

在u∗（uτ/vc）较大时，其极值表现得较为突出，即两侧的ML/M0与(ML/M0)max的差异比较明显。在u∗＞0.05之后，任务选择时，对uτ和vc的组合值要慎重设计，否则会因u∗越大而ML/M0变小，浪费质量。

此处，vc=Isp（近似值）取极大值是在上述具体数据下明显反映出来的，但我们没有给出解析式说明，据“IPM”介绍，这个研究结果出现得比较早，但经常被人们遗忘（this result is old and offen forgotten）。

2.8 关于ML=0时的极限速度

在最终速度u的表达式（14）中，其比冲是关键的参数，可以得到它的极值解析式=0。

将其结果推演如下，由式（14）可得

其中

将第二项移到等式另一端则有

此式即为u达到极值的条件，这个结果是Stuhlinger得到的。

将式（16）再代回到式（14），即将式（14）中

用式（16）的右端表达式表示，得到其umax的表达式为

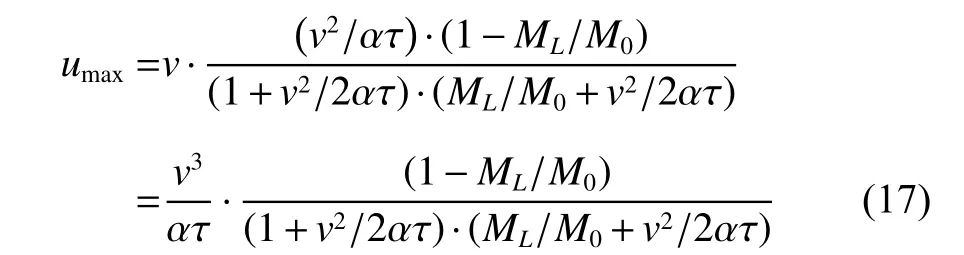
umax是在α和τ作为参数，而不是作为变量的条件下求得的。

将ML/M0从式（17）中重整有

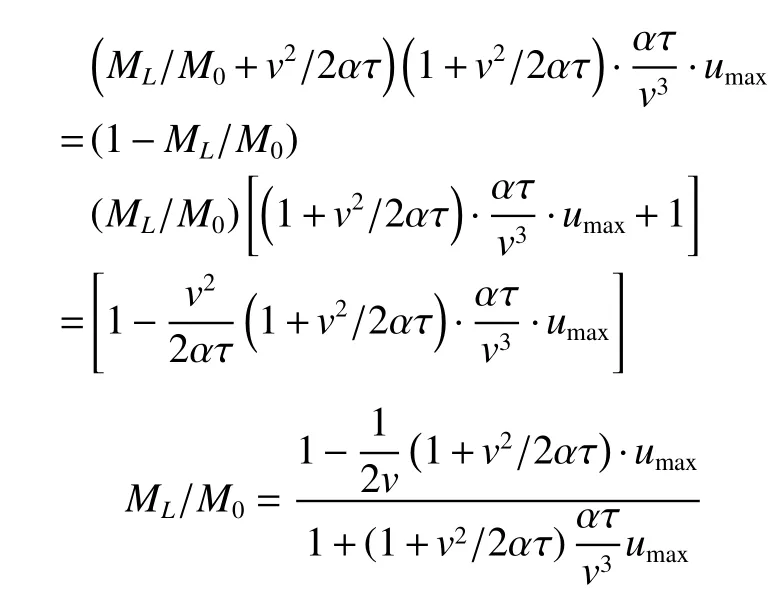
即

以上表述的就是在最终速度达到umax的时候，发动机参数α、比冲v和工作时间τ下的ML/M0的值，即任务的载荷比能力。

对于极端情况，当有效载荷为零的时候，它的最终速度将是个什么情况，也即最极限的状态下，ML=0。

这时由式（5）

我们仍对其求导得到极值速度uτmax，

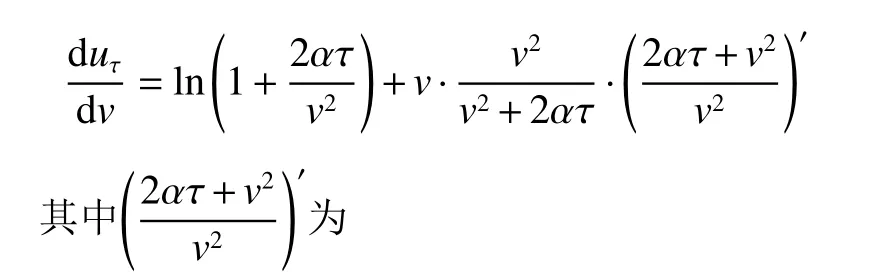
如果umax用表示时（也即比冲是特征速度的0.505倍，使u达到极值时的速度）。

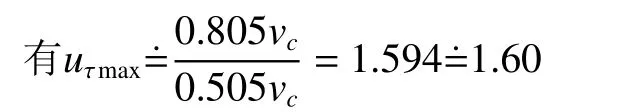
所以uτmax=1.60v是载荷比为0时的极限速度。

上述讨论的是当ML→0时的情况，由M0=Mw+ML+Mρ，当ML→0时M0=Mw+Mρ。

这个状态的物理描述，就是有效载荷ML已经不单独存在于Mw和Mρ之外。而是纳入到之中，也可以说ML不再与Mw分离，它成为动力系统的一部分，它的质量已纳入到Mw之中，并反映在发动机的功率密度α参数表达里。

这个解释，用质量定义的表达里就是

至此得到了如下关系：

当ML→0时，有Me=Mw，此时的终速最大值uτmax=1.60v（1.6倍比冲）。

将u=1.60v代入有

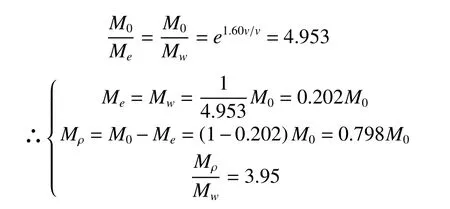
上述质量关系是从ML→0时取得的，但其结果是极具价值的，反过来讨论，也即在Mρ=0.8M0，或推进剂是干重的4倍左右时火箭的最终速度取极值，其速度可到1.60倍比冲，而此时的比冲值为0.505倍的特征速度。

在uτmax=1.60v中，v是表达在之中的，

其Mρ/MW已经上面的运算得到近似为

而在前面式（18）中

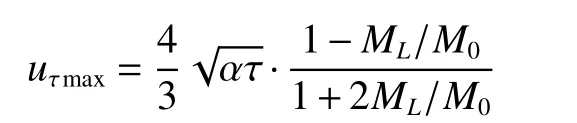
将ML→0代入

这两种方法得到的解中，以1.131 3为精确解，因式（18）是在时得到的，所以1.33则为近似解，相差近17%。

上述结论是图林格施在1964年给出去的，我感觉他不但给出了结论，而且贡献了方法。这点对我们的启发则更大，这也是我们“工程方法”论研究值得关注的地方。

当将ML的质量纳入总干重里时，如果任务要求的ML已经确定下来，则要在其它的干重质量上减重，如果发动机的MW项或火箭其它的质量降不下来，则ML就难以实现了。这是在工程权衡中值得重视的地方。

在齐奥尔科夫斯基公式或施图林格的变形表达式中，其最终速度uτ只与推进系统的质量相关，所以其它一切概念的引入实质上都是质量关系的变形。

也即(V∗)2的物理定义是推进系统干重与推进剂质量之比的物理量。

当v∗增加时，表明的相对量在增加，而推进剂Mρ的量相对在减少，所以在获得一定的速度uτ下其载荷比要下降。这点在前面分析的趋势中v∗＞1之后的下降段可以明确地看到。

一个发动机的α值和τ是相关的，也即它与任务时间要求相关，这点我们要进一步讨论。

我们验证一下ν∗=1、u∗=0.2时的载荷比ML/M0为0.637（参见式（15））。因为我们所讲的v∗为，则通过施图林格的解得到的和通过齐氏公式得到的结果必然是一致的。

∴u∗=0.2

这两者的结果是相同的。

3 深空探测的轨道转移方式

行星际飞行的基本条件是飞出地球，然后才能讨论飞往其它行星。所谓飞出地球，从动力学而言，就是地球的引力势已经近乎为零。

当飞行器的主动力工作结束，它只受空间某个主星体作用时，其“推引比ρ”为零，ρ≡a(t)/g(R(t))。

其中，a(t)表示非引力作用引起的加速度，在光帆作为推力器时它就是光压产生的加速度，此时也称ρ为“压引比”（Lightness Number），在IPM任务的中译本中称为“明度”。

g(R(t))是空间中存在的星体对飞行器产生的引力加速度。

所以我将其形象地称为推力和引力之比。在只有g(R(t))的作用下，它的运动规律完全附合我们在地球引力场中所研究的结果：

式中ri、 θ为轨道极坐标参数的矢径和近点角；µ为主星的引力常数；rp、e是轨道的形状、近拱点和偏心率；h为角动量（E为“比机械能”，即单位质量具有的能量）。

因能量是守恒的，在轨道动力学分析时，往往选择特征点（如rp、ra两点）来分析是方便的。

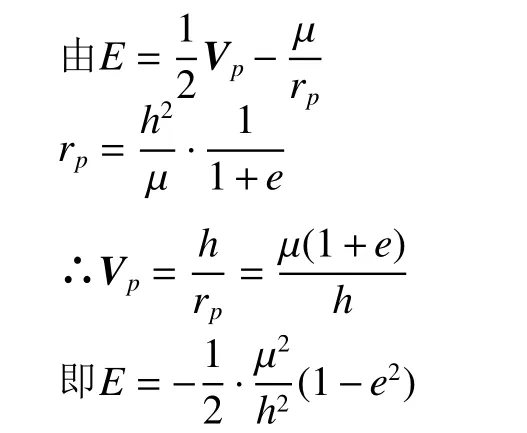
这个表达式对任何主星情况下都是适用的，只是改变其引力常数µ。

当e=1时，能量E=0

ri、Vi都随着θ角的变化而改变着，而（1+ecosθ）项将从“2”变为“0”，其r将趋于无穷，轨道是随着θ的增加而越来越远的抛物线。

由E=0有

这个近地点的速度Vp就是r可以趋于无穷的轨道速度，在深空探测中它可以完成向远程空间输送航天器脱离主星引力的基本任务。但由于此时的能量已经为零，所以它没有剩余能量飞向深远太空，我们称这个速度为逃逸速度。对深远太空而言它可以完成逃逸任务。

在e＞1时，能量E＞0

所以，不会出现θ=180°的状态，这是一条开放的双曲线。在直角坐标系描述下，此点是以纵轴为对称的一实一虚两条对称曲线，其中一条是不实现的，只是实轨道的一个影像。但在计算双曲线的半长轴时，我们还要用到这个概念（虚的远地点）。讲到这里我想加一句文外之话，在轨道动力学的研究中，其轨道的几何特征表现得很充分且有神来之意，所以我曾讲过，我们应当有一章专门讲讲“轨道的几何学”。

双曲线的奇点出现在(1+ecosθ)=0处，这时的θ=arccos(-1/e)，记作θ∞，它是在r→∞时的近点角。

由于θ是在0°～180°之间，所以有在双曲线几何里称θ∞为渐近线近点角，也称δ=2θ∞-180°为两渐近线的转向角。

因E＞0，航天器的总能量大于主星引力势且有剩余能量，靠其剩余能量可以飞向更深远的空间，但前提是g(R(t))不对其影响，而对于太阳系行星际飞行，其太阳的g(R(t))是存在的。

双曲线轨道下的总能量

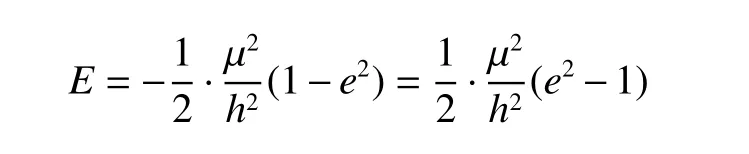
我们仍沿用ra、rp这两个特殊点来计算其能量，

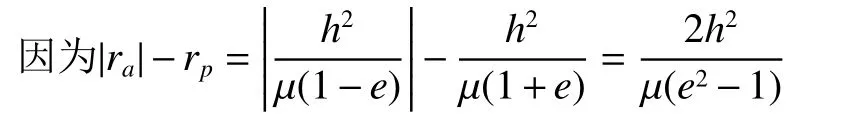
双曲线几何学的半长轴a有

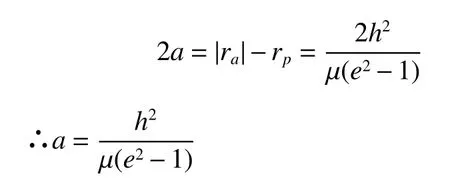
即

当r→∞时

v∞称为双曲线轨道下的剩余速度，v∞表示E，

将E和V逃逸代入（20）式，有

即

这个关系是双曲线轨道下任何一点都满足的，是一个比能量的关系（消去了质量项）。它表明双曲线轨道的总能量包括两部分：一个是超出主星中心引力逃逸所需的能量v逃逸2及超出这个逃逸能量的剩余部分。对于每个任务的不同，形成的双曲线的形状不同（即半长轴a），v∞是不同的。称v∞2为特征能量，它只与主星的引力常数µ和轨道半长轴有关，记为C3（）。

因为C3是逃逸后剩余的能量，所以要由深空探测任务给出特征值C3的需求，并在工程实践中要有充分的运载能力来保证，C3(运载)＞C3(任务)。

C3的形成是运载火箭所赋予的，从工程角度说它是任务所需求的。式（21）表明C3的大小可以从轨道的几何表达里唯一确定（即半长轴a）。

在当今的深空探测工程中，仍然是以化学推进系统产生巨大的推力将航天器送入逃逸轨道（对地球而言就是双曲线轨道），然后由航天器上的动力系统实现对目标星体的速度增量。如果我们有足够推力的运载火箭，可以实现C3(火箭)≥C3(任务需求)的条件下，则可以大大减少航天器本身的推力系统的压力。

以火星探测轨道需求，火箭提供给航天器的能量应满足

例如，对某一次具体的任务，若入轨时火箭提供的速度为11.473 km/s，

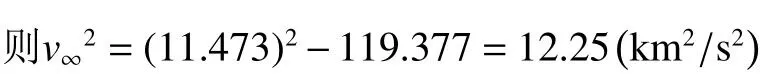
即运载火箭能够给探火星航天器的特征能量是

但对于深远空探测任务而言，只利用大推力火箭实现需求速度往往是难以办到的，因为它的比冲难以得到足够的大。而施图林格的连续推力系统是加速度积分的机理，它是在任务时间（MHJT）内完成目标的较为有希望的方案。

从已经实现的人类探测太阳系行星的工程来看，还没有实现在MHJT的理想时间内完成所关心的深远目标星的探测期望，飞行器还是需要几十年的巡航时间过程。

以我们现在的火箭能力，如果在日地影响球边缘处（距地92 500 km）使航天器具备C3，那它按这个速度奔向火星的话，它要在太阳的引力势内飞行，所以C3仍然是进入环绕太阳的大椭圆路径；如果火箭在日地影响球边缘处使航天器具有逃逸太阳的能量，则这时的剩余能量则可以直奔太阳系边缘而去，而不受太阳引力势的作用，那么这个速度应当是多少呢？

我们先计算在地面脱离地球的能量

在地表处地球自转的牵连速度

要想脱离地球引力势，其速度一定要大于（11.18～0.465）k m/s。在日地影响球半径（rSOI=9.25×105km）时，地球引力势和太阳引力势分别为

可见此时太阳的作用是地球的2 000倍，所以此时只考虑太阳的作用是合理的。

怎样实现从原轨道向目标星轨道的大椭圆转移呢？

如果设定这个转移时刻是准确的，则在航天器飞行到目标星的预测点时，目标星也正好到达该点，两者交会。太阳系内各行星的运动规律我们已经充分掌握，所以这个假定在工程上是可以实现的。但深空探测对空间飞行体的跟踪与观测要求要比近地空间活动更高，在下面讨论的转移轨道问题中，精确的外测保证是十分重要的条件。

当航天器已经脱离了地球的引力势，我们的分析就只是太阳和航天器的两体问题。若此时航天器的位置是A，目标星的期望到达点是B。（也即是两者交会点的期望值。）

我们的任务就是要构建一个大椭圆轨道，使其成为霍曼轨道上的两个点，且目标星位置正是近点角为π的远地点B。（见图1）

图1 新构建的大椭圆轨道Fig.1 The large elliptical transfer orbit

将新构建的轨道参数写作rn、θn、hn、en，其拱线为目标星的期望点B与主星中心的连线，已知的参数是θnA，rA、rB以及主星的引力常数µ。

从轨道方程

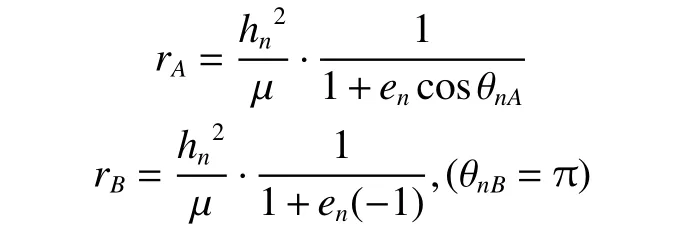
其中hn和en是两个待求量

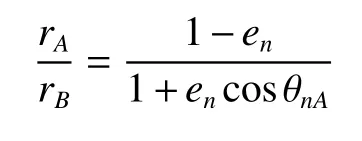
得到

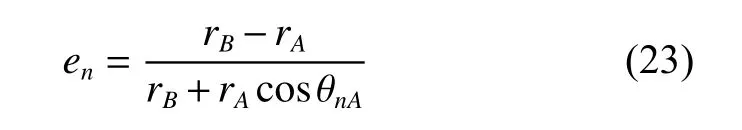
将en代入rB式，有

得到en和hn就得到了这个新构建的从A点到B点的一个大椭圆轨道。

这是从轨道的几何关系里求得的，但这个轨道能否实现，要看工程上能不能使值达到这个能量需求。

A点的能量需要也即轨道的需求速度，A点的速度VA可以分解为对矢径的径向和垂向两部分组成，

其中垂向

径向Vnr是矢径rn方向的速度，也即

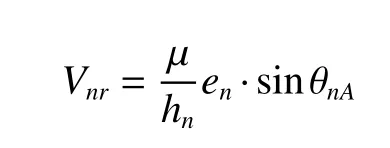
则所需的速度矢量与航天器和主星中心的连线的夹角（称为飞行路径角）γ的正切值tanγ=Vr/V⊥，则

以上讨论的就是在太阳系的行星际探测中大椭圆转移的方式。不论其初始轨道时的状态为何，最终都要满足我们分析的状态。

工程实践上就要在测控系统的支持下完成V⊥,Vr及飞行路径角γ的实现。

针对连续推力的施图林格方案，在g(R(t))的作用相对a(t)已经很小时，比如在太阳帆方案时，太阳帆飞行器的质量比较轻。

下面我们就连续推力的太阳帆的有关问题作为例子来讨论。

太阳光直射太阳伞反射面时，它的平面功率密度为1368 w/m2（地表面处）

功率是力与速度之积，而光速是已知的，所以其地表处的太阳光压P可以表示为

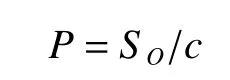
其中：SO为太阳辐射功率（1 368 w/m2）；c为光速（以3×105km/s计）。则地球表面的太阳光压为

我们讲的“压引比”，则是太阳帆上的太阳辐射压力与太阳帆所受太阳引力的比值（The lightness number，which is the radio of solar radiation pressure force on the sail to solar gravilation force on the sail）。这个定义与“推力引力比”的概念是一样的，如果不是太阳帆，而是其它的推力系统，则这个比值则可统称为“推引比”，即ρ=ac(t)/g(R(t))，其中ac=P/m，如果都以太阳帆面积A作为衡量的基准，则P是单位面积上分摊的动力（P/A，单位是N/m2），而m则是单位面积的质量，即有

其中：σsail为太阳帆的面质量密度；mPL为航天器有效载荷质量；A为太阳帆的面积。

在实际工程上还要考虑太阳帆的反射率、为控制合理温度而增加的太阳帆结构涂层的发射率等，还有太阳光入射方向与太阳帆法线的太阳光压角等因素要在q⊥上得到反映，即形成有效光压Peff。在垂直入射时，

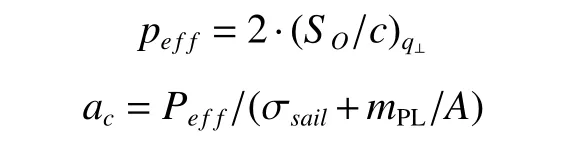
若Peff按2×4.56µN/m2计算，

A为100 m2，σsail=10 g/m2，mPL=10 kg

则在地球附近可获得的加速度为

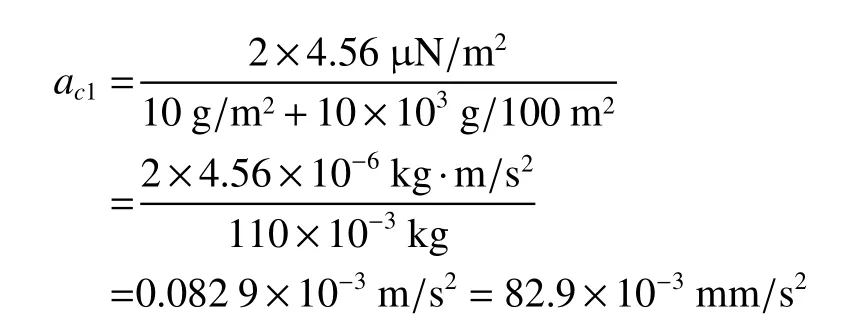
如果仍保持太阳帆的总质量不变，而将σsail从10g/m2降到1g/m2。则因太阳帆总质量不变，所以其帆的面积将扩大10倍；相应的mPL/A将缩小10倍，其加速度将为

所以σsail是极其重要的技术参数。

在G.L.Matiloff的“Deep-Space Probes，2nded，中给出了另一种表达式[3]

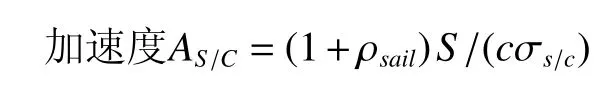
其中：ρsail为太阳帆对日光的发射率；S为单位时间照射到太阳帆单位面积的太阳能S=SO/r2，r为太阳距地球表面距离r0与航天器距太阳距离r之比，以AU为单位；c为光速；σs/c为压引比。

在这个表达式中，光压为(1+ρsail)S/c·r2，我们把加速度AS/C整理为两部分

第一部分是自然参数，太阳辐照S，光速c和距太阳之距r；

第二部分是与太阳帆航天器相关的物理参数，帆的反射率ρsail和航天器的帆面积的分摊质量σs/c。

定义ηs/c(1+ρsail)/σs/c为“压引比”，

（1+ρsail）项表示太阳帆具有的光压，而σs/c则表示是受到引力作用的质量项。是光压与引力之比，这也是将其称为压引比的原因。

如果我们将“外太阳系”理解为仍在太阳引力范畴，这里的行星体仍以太阳为主星，环绕太阳运行。而不是指“太阳系外”的其他星系。这就把“Outersolar System”和“Outer Space”分开了。（但这点只供参考）

在20～30年的“MHJT”可承受时间内要求到达200 AU处。则航天器的平均飞行速度不能小于7 AU/年，

逃逸太阳的速度

因地球的公转速度是可以利用的。

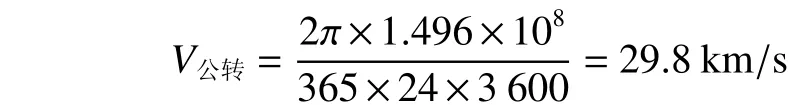
速度增量

对于一个脱离太阳引力的航天器，首先要具备逃逸地球的能力，所以从地球出发的航天器应具有的能力应为

这就是从地球表面出发脱离太阳引力的第三宇宙速度。

这对目前的火箭能力而言是难以实现的。

美国新地平线实现的C3≅160 km2/s2，它要奔赴100 AU处需37年以上。

即使我们采用太阳帆或利用太阳能的电推进系统，都会因为随着飞离太阳的距离增加而衰减。这也给航天器携带高比冲的连续推力系统方案加了权。还有一个问题是，如果有对目标星体的环绕探测或驻留特殊点的探测要求时，一定要具备航天器的制动能力。我们在前面有关连续推力过程中没有涉及制动阶段（Braking Stage）的问题。

在太阳帆技术的研制方面，我认为材料的研制是关键，特别是帆载荷σ，这是个关键参数。

以石墨烯的应用为例，其面质量密度是有希望达到1 g/m2的。碳原子间距约为0.14 nm ，所以在1m2的面积内，可布有51×1018个碳原子（1m2/(0.14×10-9)2m2）；

原子质量单位1u≅1.66×10-27kg=1.66×10-24g

碳原子为12个原子质量单位，则1 m2的质量为51×1018×12×1.66×10-24g/m21mg/m2，如果能采用这个轻质材料的资源，根据太阳帆工作状态下的热量、刚度、展开强度等工程要求而增加其它的聚合物，是可以在1g/m2的指标下，有所作为的。

NASA在1999年提出的星际探测方案中，质量只有几百千克，其中有效载荷25 kg，太阳帆直径400 m。初始椭圆轨道近日点0.25～0.3 AU，航天器在此处展开太阳帆，借助近太阳的辐射压，此处是地球（1 AU）处的16～11倍。报告称，它可以让航天器在大约20年内到达太阳风层顶（200 AU处）。

以上说明的是连续推力系统的深空探测问题。还有一种方案是选择相应的机会，利用空间天体的g(R(t))做动力，这种方式被称为行星际探测的借力飞行问题。

就其深空探测的轨道实现而言大致包括3种可采用的方式：连续推力系统，脉冲推力的大椭圆转移和空间的借力飞行。

关于连续推力系统中受到重视的是太阳帆离子推子和核动力，有关这些方面的技术研究要引起关注。

后 记

施图林格提出实现太空船的电力推动问题可能是在二战期间，但他在《离子推进的空间飞行》一书中所引用的文章《Possibilities of Electrical Space Ship Propulsion》是在1954年发表，不知他是否还有更早时间发表的文章中谈及电力推进的概念。

我得到IPM（Interstellar Precursor Mission）是在2013年IAA会议上，由中国宇航出版社出版，主编是（美）Claudio Bruno及（美）Gregory Mattoff，中译本译者是陈杰、殷前根先生。

看过之后，启发诸多，总想把其中的几个重要的概念性东西（比如施图林格精确解的推导；精确解中应当单独提出来的几个概念；太阳帆的压引比及最终速度uτ的分析等）解析一下，今天算初步做了一点讨论。

为了能得到施图林格的原著《Ion Propulsion for Space Flight》全文，我请国家国防科工局科技与质量司及中国航天科技集团有限公司系统研究院的同志帮忙，他们费了不少功夫，总算找到，并复印给我。据说原本已经很陈旧，共373页，署名ERNST STUHLINGER（George C.Marshall Space Flight Center National Aeronalics and Space Administration）。在这里感谢同志们的帮助，使我看到了原著，也让我思考了不少东西。特别是施图林格从齐奥尔科夫斯基公式中提出“功率密度”，并展开一系列推演的思路，是具有科技方法论意义的。

我希望在研究深空探测的推力系统和工程的实施方案时能关注施图林格的方法和成果，并能有所创新和发展。

附录：

在施图林格的原著和IPM的任务中有若干图表，这些图表的形成我用“计算任务书”的形式表达如下，供有兴趣者参考。

（任务书1）：求有效载荷比与比冲的关系

以ML/M0为纵轴（最小值0，最大值1.0，分格间隔0.2），logv∗为横轴（v最小值0.01、最大值为10，分格按步长0.01），以uτ∗为参数，计算=或=(1+v∗)e-uτ∗/v∗-v∗2。

uτ∗分别为0.01，0.02，0.05，0.1，0.2，0.3，0.5，0.6，0.7，0.8，0.81时,v∗=0.01～10，步长0.01，计算ML/M0并对每个uτ∗下的数据连成曲线。（得到文献1之图4-1）

（任务书2）：

任务距离Sτ=73 AU

以ML/M0为纵轴（最大值为1.0，分格间隔0.1），为横轴（最小值50 km/s，最大值500 km/s，分格间隔50 km/s），

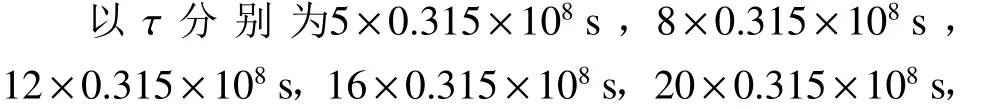
以α=0.1×10-3km2/s3为固定参数，24×0.315×108s ，28×0.315×108s 条件下，变量v由50～100km/s，步长50 km/s的，J=1-，

求解：

得到ML/M0，按每一τ值下的ML/M0连成一条曲线。

（得到文献1之图4-2）。

（任务书3）：

任务距离Sτ=73 AU

以ML/M0为纵轴（最小值0.3，最大值为1.0，分格间隔0.1），v为横轴（最小值50 km/s，最大值500 km/s，分格间隔50 km/s），

与任务书2相同，将τ=20×0.315×108s作为固定参数，在α分别为0.1 kw/kg （0.1×10-3km2/s2）、0.2 kw/kg 、0.3 kw/kg 、0.4 kw/kg作为参数条件下，以v为变量，v从50～500 km/s、步长50 km/s，

求解：

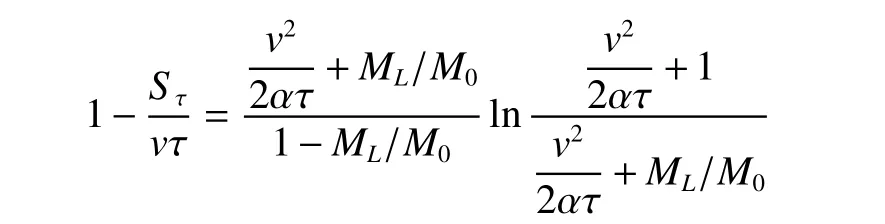
得到ML/M0，按每一α值下的ML/M0连成一条曲线。

（得到文献1之图4-5）。

（任务书4）：

任务距离Sτ=540 AU

以ML/M0为纵轴（最小值0，最大值为0.3，分格间隔0.05），v为横轴（最小值50 km/s，最大值500 km/s，分格间隔50 km/s），

以α=0.1×10-3km2/s3为固定参数，

在τ=22×0.315×108s 、24×0.315×108s 、28×0.315×108s情况下，以v为变量，v从50～500 km/s、步长50 km/s，计算施图林格通用精确解，

求解：

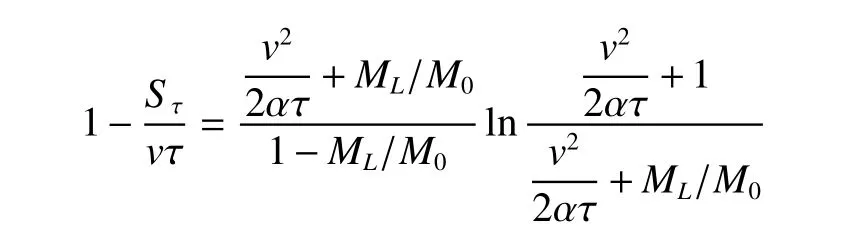
解出相应ML/M0，按每一τ值下的ML/M0连成一条曲线。

（得到文献1之图4-6）。

（任务书5）：

任务距离Sτ=540 AU

以ML/M0为纵轴（最小值0，最大值为0.6，分格间隔0.1），v为横轴（最小值50 km/s，最大值500 km/s，分格间隔50 km/s），

以τ=24×0.315×108s 为固定参数，在α=0.1×10-3km2/s2、、0.2×10-3km2/s2、0.3×10-3km2/s2、0.4×10-3km2/s2情况下，以v为变量，v从50～500 km/s、步长50 km/s，求解施图林格通用精确解：

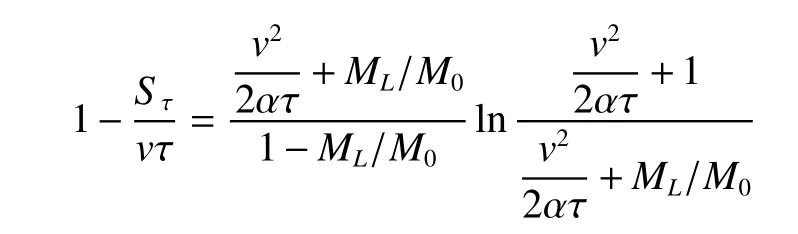
解出相应ML/M0，按每一α值下的ML/M0连成一条曲线。

（得到文献1之图4-7）。

（任务书6）：任务时间τ（年）与功率密度α的关系

Sτ分别为73、100、540、730 AU，

τ以年计，v以km/s计，时

计算施图林格通用精确解：

求解L，因J、L中含有ML/M0、α、τ、v、Sτ五个参数，此题可以按4种组合分别计算。

1）v=50 km/s，ML/M0=0.1，

Sτ分别取73、100、540、730 AU，

求τ与α的关系。

施图林格解：

令α依次取0.1、1、10、100、1 000、10 000，可得到相应的τ。

以τ为纵坐标（最小值0，最大值为100，分格间隔20），以log∆=为横坐标作图（最小值0.1，最大值为10 000，分格间隔log∆=1，即从-1～4）。

变换Sτ则得到另一条关系线。

此图有对应Sτ的4条关系线。

该图即为文献1之图4-8。

2）v=50 km/s，ML/M0=0.6，

其余过程同1。

作图：其纵轴τ最小值为0，最大值为320，分格间隔40；α最小值为0.1，最大值为10 000，分格间隔log∆=1。

得到的关系即为文献1之图4-9。

3）v=350 km/s，ML/M0=0.1，

其余过程同1。

作图：纵轴最小值0，最大值40，分格间隔10；横轴最小值0.1，最大值为10 000，分格间隔

log∆=1。

得到的关系即为文献1之图4-10。

4）v=350 km/s，ML/M0=0.6，

其余过程同1。

作图：τ纵轴最小值为0，最大值为70，分格间隔10；α横轴最小值为0.1，最大值为10 000，

分格间隔log∆=1。

得到的关系即为文献1之图4-11。

（任务书7）：求解功率P与比冲v的关系

求解步骤如下：

1）首先求截比J

在τ=20年、Sτ=73 AU任务条件下，

令vi=50 km/s～500 km/s、步长50 km/s，

则J是一个简单的计算，可得下表：

求解Qi

3）由

4）以M0分别为10、100、1 000、10 000及100 000 kg计算相应的Pi，（M0，vi，Qi已取值）

5）以logP为纵轴，以v为横轴，画出P与v的关系

作图：纵轴logP的最小值为1，最大值为7，（即1.E+0.1～1.E+0.7），横轴v最小值50km/s，

最大值500 km/s，步长50 km/s），

则得到文献1之图4-12。

6）以Sτ=73 AU、τ=8年任务条件下重复上述（1～5）

步骤，作图的各坐标标度与上面相同。

得到文献1之图4-13。

7）以Sτ=540 AU 、τ=24年任务条件下重复上述（1～5）

步骤，作图的各坐标标度与上面相同。

得到文献1之图4-14。