基于collocation方法的Taylor-Culick模型流动稳定性的特征向量分析①

李 阳，刘佩进，金秉宁

(西北工业大学 燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

固体火箭发动机(如美国的Space Shuttle SRM、RSRM、Titan系列以及欧洲的Arian 5 P230)工作过程中容易出现轴向、低阶的压强振荡和推力振荡[1]。由于发动机几何尺寸较大，工作时间又很长，在实际预估中，对每一时刻的工作状态进行数值模拟是不现实的。因此，在流动稳定性机理研究的基础上，谱方法作为一种快速预估手段，可用来分析流动不稳定特征以及演化规律。

国外自20世纪60～70年代开始，利用稳定性理论分析固体火箭发动机的流动稳定性。Varapaev和Yagodkin最先在平行流的假设下，研究了Taylor平面流的流动稳定性，导出了流函数表示的类似Orr-Sommerfeld方程的扰动方程，得到中性曲线[2〗。Casalis等对Taylor平面流的稳定性做了更加深入的研究，但结果与Varapaev和Yagodkin的结果有一些差异[3]。后来，Griffond发现了上述差异产生的原因是由于所用变量不同所致[4]。由主变量和流函数所表示的扰动方程不同，但所得结果差异不大。Akiki研究可压缩Taylor平面流的稳定性时出现了幅值的偏差，认为最主要的原因可能是解析方法把有旋量和无旋量分开去求解，而数值方法是整体求解[5]。但Chedevergne发现，解析涡声解和流动稳定性模态的叠加可准确地重现DNS结果。因此，Akiki的解释并不令人信服[6]。除了Taylor流模型，Griffond[4]利用Taylor-Culick模型，使用了打靶法，得到了其两个不稳定频率，并分析了中性曲线和增长因子。国内对于固体火箭发动机内部流动不稳定性的研究较少，杨尚荣应用局部非平行理论分析了关于主变量和流函数导出的扰动方程的差异，比较了基于空间发展模式的理论结果与大涡模拟计算结果[7]。稳定性预估方法在Taylor平面流的研究中已获得一定进展，但平面模型显然与实际发动机差别较大，更合理的模型是Taylor-Culick流。虽然Taylor-Culick流更接近实际发动机，但不可避免的将引入柱坐标，其对称轴处在数值计算时产生奇性，影响计算结果的准确性。

本文利用谱配置法对Taylor-Culick流动模型进行稳定性分析时，利用配置微分矩阵的方式处理了对称轴处奇性的问题，与Griffond[4]利用打靶法相比，不需要选择初值，减少了人为因素的加入，适应性更强，且计算更为简便。国内外对于固体火箭发动机内部流动不稳定现象的研究主要关注于流动不稳定发生的可能性及频率，但对于流动不稳定所产生的影响及不稳定的局部特征没有相应的分析。对于不稳定特征研究，可更有效地揭示流动不稳定现象，并启发对于流动不稳定的抑制。因此，本文还分析了不同不稳定频率下的特征向量，用来反映流动不稳定的局部特征。

1 Taylor-Culick流方程处理

1.1 物理及数学模型

本文研究的径向加质Taylor-Culick流几何构型与坐标见图1。

采用不可压粘性流体N-S方程，利用归一化参考量：半径R、径向加质速度Vinj、密度ρ和运动粘性系数ν进行无量纲化。并将瞬时变量分解为平均量和扰动量的和，得到扰动方程：

·u′=0

(1)

平均量作为基本流，可事先求出解析解[8-9]：

(2)

利用分离变量法，假设扰动量为简正模态形式：

=(ur,uθ,uz,p)(r)ei(mθ+αz-ωt)

(3)

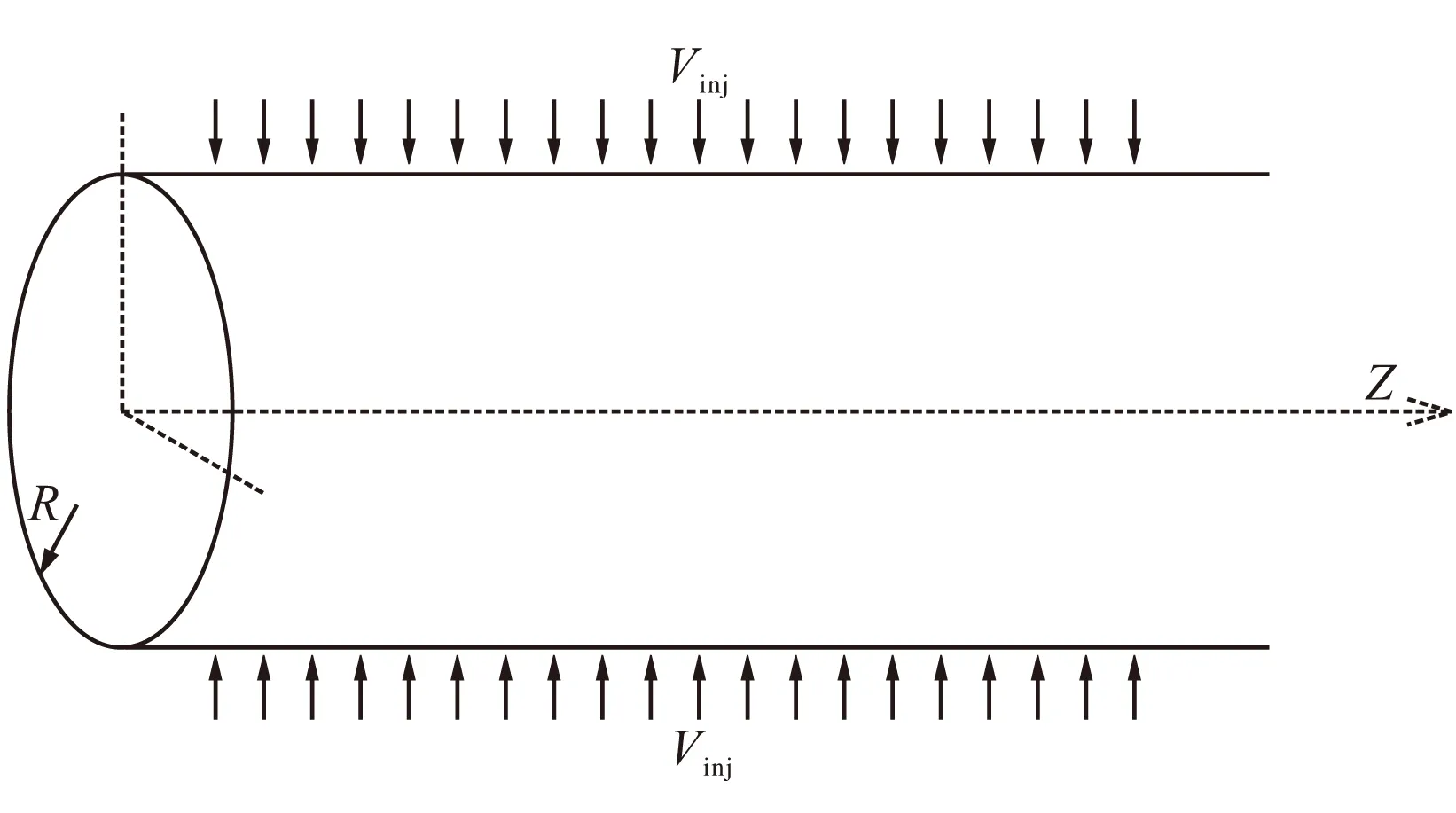
图1 几何模型

进行空间稳定性分析，ω为实数，代表无量纲时间扰动频率，α=αr-iαi为复数，实部αr为轴向扰动频率，负虚部αi为轴向扰动局部增长率。m为正整数，代表环向波数。将上式代入扰动方程中，得到如下关于α的多项式特征值问题：

(4)

矩阵L的元素Lij分别为

Taylor-Culick流的边界条件为壁面上的速度边界条件：头部壁面速度为零、轴向坐标轴上的速度对称条件、侧壁上注入速度为常数以及侧壁上的无滑移边界条件。利用扰动量表示物理边界条件得到扰动方程的齐次边界条件,利用扰动方程还可得到压力边界条件。

(ur,uθ,uz)(±1)=0;Dp(±1)=0

(5)

确定时间扰动频率ω和环向波数m后，便可利用谱配置方法求解特征值问题，得到任意轴向位置z处的频率ω对应的增长率αi和频率αr。

1.2 微分矩阵的建立

由于配点法所假设的近似解是在定义域内关于配点对未知函数进行的高阶多项式插值逼近，所以可对该插值多项式进行微分，得到微分矩阵：

(6)

完成对未知函数导数项的逼近，进一步建立微分算子矩阵的具体形式(式(6))[10]。

高阶微分矩阵由下面公式计算得到，l阶微分矩阵为一阶微分矩阵的l次方。

D(l)=(D(1))l,l=1,2,…

(7)

由于计算采用柱坐标，稳定性方程会出现含有1/r和1/r2的项，这些项的值在轴线r=0处无穷大，对称轴处出现奇性，需要在数值计算时特殊对待。本文考虑到在计算矩阵算子时，边界r=0在矩阵中始终表现为块矩阵的一行，而矩阵之间只有加减运算而不做矩阵乘法。也就是说，奇性始终作用在边界点上，不会进入到内部节点的计算中。

矩阵算子中边界点上的值最后会被r=0处的边界条件替换掉。因此，本文直接令r=1参与r=0处的计算，然后用边界条件替换掉矩阵算子中r=0所在的行向量。这样既可提高精度，又可解决对称轴处奇性的问题。图2阴影所示为L矩阵配置位置，分别为分块矩阵r的倒数项对应于r=0所在的行。

1.3 计算结果验证

为验证算法及程序，计算了长径比z=10，雷诺数Re=4500，时间波动频率ω=80，环向波数m=0下的不稳定模态，得到的特征谱如图3所示(图中坐标无量纲)，存在两个不稳定模态。与Griffond的结果[4]比较，结果如表1所示。

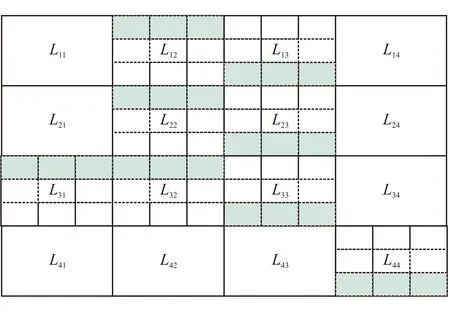
图2 L矩阵配置位置

模态Griffond的结果[4]本文结果误差/‰1αr6.095 294 565 66.095 295 97αi-1.078 799 814 0-1.078 801 377<12αr3.326 428 536 63.326 428 826αi-0.109 552 558 9-0.109 552 685 1<1

图3 特征谱

本文所得结果与文献结果基本吻合，可验证本文所用方法可行。误差在1‰以内，满足精度要求。

2 结果分析

对于3个不同频率ω，特征值α=0对应的无量纲特征向量见图4。随着时间波动频率的增大，径向的振荡周期变小，振动幅度减小。这说明时间波动频率与径向波动频率是同步的，振动频率越小，振动幅度越大，使得振荡渗透向轴心(r=0)处的深度也更大。频率越低的不稳定振动，影响范围越大。

图5比较了3种雷诺数下，特征值α=0对应的无量纲特征向量的变化。随着雷诺数的增加，振动幅度变化不大，但振荡波向内部的渗透深度变大，振幅的衰减率减小。径向加质速度越大，雷诺数越大，振动可在幅度不变的情况下影响范围越大。流动不稳定现象所表现出来的是流体振动的失稳，其特点与一般振动所表现的效果相似。从特征向量可看出，流动失稳首先从壁面开始，逐渐向中心渗透，频率与振幅呈反比例增长。

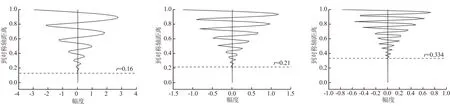
(a) ω=30 (b) ω=50 (c) ω=80

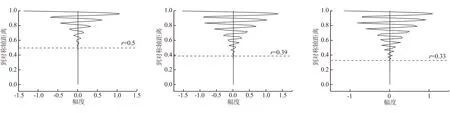
(a) Re=900 (b) Re=2000 (c) Re=4000

可从能量的角度进行分析: 当总能量保持不变而频率变化的情况下，高频振荡从壁面注入后很快衰减，低频振荡衰减较慢，能够更深入地渗透到流动区域内；雷诺数的变化同时反映了能量的变化，振荡从能量注入的位置开始，向内部渗透，能量越大，渗透的深度越深。流动稳定性的特征向量变化表现出阻尼振荡的特征。整体的能量注入、能量传递、能量耗散和能量随流动流出控制区域的形式和变化，还有待后续工作进行阐述。

3 结论

(1)对于对称轴处的奇性，可利用配置矩阵的方式进行处理，相比打靶法过分依赖于由经验所给定的初值，其实用性更强，更适用于计算机计算。

(2)分析了Taylor-Culick不同条件下的特征向量，得到了其流动不稳定局部特征。流动不稳定由能量注入处发生，雷诺数越大且频率越小，渗透部分越深。这意味着大雷诺数的低频振荡输入对应的模态振型对内部的作用更强烈，影响流场的范围更大。由于非线性理论可分析有限幅值振荡，建议在后续工作中考虑非线性因素的影响。