一类随机模糊细胞神经网络的输入对状态稳定性分析

周伟松, 王兴武, 吴东海, 曾 豪

(重庆邮电大学 工业物联网与网络化控制重点实验室/复杂系统智能分析与决策重点实验室, 重庆 400065)

1988年,Chua等[1]首次提出一类如下形式的神经网络模型

此模型后来被称为细胞神经网络(CNNs)模型.由于CNNs在图像处理、联想记忆、模式识别、二次优化等诸多领域的广泛应用而受到众多学者关注[2-9].文献[2-4]将模糊集理论融入到CNNs,建立了如下模糊细胞神经网络(FCNNs)

的系统理论及其应用,给出一个新的图像处理范例.鉴于它在学习、适应、容错、并行和泛化等方面的计算优势,迅速成为图像处理、模式识别等问题的强有力的工具[5-9].

在FCNNs的众多应用当中,保证FCNNs系统的稳定性显得尤为重要[10-12].例如,当将FCNNs应用于优化计算时,网络的平衡点刻画了该优化问题的所有可能的最优解,而且平衡点的全局渐近稳定就可以确保从任何初始条件出发的最优解的收敛性.从而,稳定性是研究FCNNs的重要课题之一[13].

另一方面,由Sontag[14-15]对非线性系统控制所提出的输入对状态稳定(ISS)是对非线性系统研究中一类非常重要的耗散性质.而且,它给来自工程控制应用当中许多不确定因素存在的非线性控制问题的稳定化提供了一种非常有效的方法.再者,白噪声和时滞都是动力系统中广泛存在的现象,并且时常不可避免,都会引发系统的不稳定,甚至混沌.因此,研究带随机泛函FCNNs具有非常重要的理论和实际意义.然而,据我们所知,现在关于随机泛函FCNNs在均方意义下的指数ISS的结果还没有.

基于上述讨论,将在本文中给出一类带时变系数的随机泛函FCNNs在均方意义下的指数ISS的2个充分条件.首先,给出一些基本概念、定义以及引理.特别地,建立了一个非常有用的Halanay型非自治泛函微分不等式引理.然后,运用这个引理得到了一个随机泛函FCNNs在均方意义下指数ISS的一个充分性判据.而且,在这个基础上,给出了一个常系数情形下的该FCNNs系统在均方意义下指数ISS的充分性判据.最后,给出一个数值仿真例子证实得到判据的有效性.

1 预备知识

本文将考虑如下带时变系数的随机泛函FCNNs[2-4]

其中,i=1,2,…,n,并且,对于每一个i,xi(t)表示在t时刻第i个神经元的状态变量,φi(t)在区间[-τ,0],τ>0上连续,di(t,xi(t))是依赖于时间t和状态随机过程xi(t)适当的一个行为函数,Ii是第i个神经元的外部输入量,aij(t)、bij(t)和cij(t)描述t时刻神经元之间状态链接的强度.∧和∨分别表示模糊并和模糊或算子.fj(xj(t))、gj(xj(t-τ(t)))和kj(xj(t-τ(t)))分别表示t和t-τ(t)时刻第j个单位元的激励函数.τ(t)是时变时滞,而且满足0≤τ(t)≤τ.σij(t,xj(t),xj(t-τ),xj(t-τ(t)))项是漂移系数,并且是一个Borel可测函数.ωj(t),j=1,2,…,n是定义在一个完备概率空间(Ω,F,P)上并且带有一个自然滤波{Ft}t≥0标量标准Brown运动.

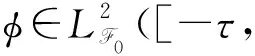
E|x(t;φ)|2≤αe-βtE‖φ‖2+γ|u|2.

定义1.2假设矩阵D=(dij)n×n,其中dii>0,并且dij≤0,i≠j,i,j=1,2,…,n,那么以下3个条件任何一个都等价于“D是一个非奇异的M矩阵”[17-18]:

(i)D的所有顺序主子式都为正;

(ii)D-1(D的逆矩阵)存在并且D-1≥0;

(iii) 存在一个正向量p使得Dp>0或者DTp>0.

为了得到主要结论,首先对方程(1)当中的系数函数作出一些常规的假设.此外,都假设这些系数函数在定义域当中都是Borel可测的.对i,j∈N≐{1,2,…,n},假设以下条件都成立:

(H2) 激励函数都是全局Lipshitz连续的,也就是说,存在正常数Li、Mi、Ni,使得对于任意的t∈[0,∞)和x,y∈R有

|fi(x)-fi(y)|≤Li|x-y|,

|gi(x)-gi(y)|≤Mi|x-y|,

|ki(x)-ki(y)|≤Ni|x-y|.

(H3)fi(0)=gi(0)=ki(0)=0,σij(0,0,0)=0.

(H4) 存在非负函数μij(t)和νij(t)使得

|σij(t,x,y)-σij(t,x′,y′)|2≤

μij(t)|x-x′|2+νij(t)|y-y′|2,

其中,x,x′,y,y′∈R.

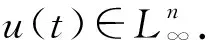
为了方便计算,将要应用以下2个引理.

引理1.1[3]假设fj(x)是定义在R上的函数,那么对于任给的aij,xj,yj∈R,i,j∈N,都有如下估计:

为了得到系统(1)的MSE-ISS,首先建立以下Halanay型非自治泛函微分不等式.

引理1.2设b∈(0,+∞),υi(t)∈C([0,b);R)是如下带初值条件υi(t)∈PC([-τ,0];R),i∈N的泛函微分方程的解,且

qij(t)[υj(t)]τ]+Ii, t≥0,

(2)

其中D+(·)是函数(·)的右上Dini导数并且

pij(t)≥0,i≠j,

qij(t)≥0, Ii≥0,i,j∈N.

如果存在正常数λ使得

(3)

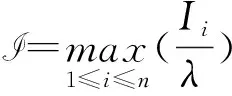
υi(t)≤ke-λt+I,t≥0,

(4)

其中初值函数满足

υi(t)≤ke-λt+I,t∈[-τ,0].

(5)

证明为了获得结果,这里令ui(t)=υi(t)-I,那么,根据(5)式可得

ui(t)≤ke-λt,t∈[-τ,0].

(6)

首先,将证明对于任给的正数ε和i=1,2,…,n有

ui(t)≤k*e(-λ+ε)ty(t),t≥t0

(7)

成立,其中k*=keετ.如果(7)式是不正确的,那么根据初始条件(6)以及ui(t)在区间[0,b)上的连续性,一定能找到一个常数t*>0和某个正整数m使得下面2式成立:

um(t*)=y(t*),D+um(t*)≥y′(t*), (8)

ui(t)≤y(t),t∈[-τ,t*],

i=1,2,…,n.

(9)

利用(2)式和(8)～(9)式有

D+um(t*)=D+υm(t*)≤

bmj(t*)([uj(t*)]τ+I)}+Im≤

bmj(t*)k*e(-λ+ε)(t*-τ)}+Im+

bmj(t*)k*e(-λ+ε)(t*-τ)}≤

-k*λe(-λ+ε)t*<

k*(-λ+ε)e(-λ+ε)t*=y′(t*),

(10)

这是与不等式(8)相矛盾的.因此(7)式对于任给的t≥t0都成立.最后,令ε→0,得到

ui(t)≤ke-λt,t≥0,i=1,2,…,n,

即

υi(t)≤ke-λt+I,t≥0,i=1,2,…,n.

证明完毕.

注1相比文献[16]中的引理3.1,该引理中可控输入项Ii和指数收敛率λ都是常数.特别地,(3)式中不等号是“<”,而不能是“≤”.

2 主要结果

分析和研究FCNNs系统(1)的MSE-ISS性质.

定理2.1假设条件(H1)～(H4)都成立,并且存在正常数λ使得

其中

那么系统(1)是MSE-ISS的.

证明首先,构造一个Lyapunov函数

(13)

dVi(t,x(t))=LVi(t,x(t))dt+

Vix(t,x(t))σ(t)dω(t),

(14)

其中

进一步地,根据条件(H1)～(H4)以及引理1.1,得到It算子LVi(t,x(t))满足

LVi(t,x(t))=2xi(t)[-di(t,xi(t))+

-2xi(t)di(t,xi(t))+2|xi(t)||Ii|+

-2xi(t)di(t,xi(t))+2|xi(t)||Ii|+

|gj(xj(t-τ(t)))-gj(0)|+

|kj(xj(t-τ(t)))-kj(0)|+

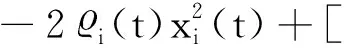
Nj|cij(t)|)-Li|aii(t)|-μii-

Hij(t)[Vj(t,x(t))]τ}+Ui,i,j∈N,

(15)

其中Tij(t)、Hij(t)是由(12)式决定的,且

根据文献[6]中定理2,系统(1)有唯一的全局解x(t),并且EVi(t,x(t)),i∈N在t≥0上都连续.另外,根据(14)式有

EVi(t+Δt,x(t+Δt))=

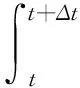
(16)

最后,假设

EVi(t,x(t))≤E‖φi‖2e-λt+U,t≥0, (17)

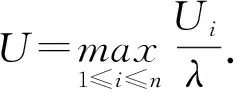
对于初值条件xi(ϑ)=φi(ϑ),ϑ∈[-τ,0],可得

E‖φi‖2e-λϑ, ϑ∈[-τ,0].

(18)

然后,由条件(11)和引理1.2,可得

EVi(t,x(t))≤E‖φi‖2e-λt+U,t≥0. (19)

结合(18)和(19)式得

αe-λtE‖φ‖2+γ|I|2,

(20)

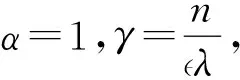
为了研究系统(1)的MSE-ISS,假设以下条件：

那么,系统(1)是MSE-ISS的.

(22)

说明系统(1)是MSE-ISS的.证明完毕.

注2.1定理2.2是文献[16]中推论2.1的推广.事实上,文献[16]中定理2.1是定理2.1的特殊情形,再加上条件(H5)和(H6)都成立,易得文献[16]中的推论2.1.

3 数值仿真例子

例3.1考虑如下n=3时带时变系数的FCNNs(1):

f1(x)=cosx,f2(x)=tanhx,

k1(x)=k2(x)=k3(x)=

另外,ω(t)是一个二维标准Brownian运动,系统(1)其他参数全部为零.

显然地,当选取

时,条件(H1)成立.通过三角不等式

|cosu-cosv|≤|u-v|,

|tanhu-tanhv|≤|u-v|,

可得到f1、f2和f3都是全局Lipschitz连续的,而且可以求得Lipschitz常数为L1=L2=L3=1,同理可以得到

即说明假设(H2)成立.另外,假设(H3)显然是成立的.此外,当取

时,条件(H6)成立.

当选择λ=1.17时,可以很容易地计算得到,对于任意的t≥-2,有

因此,根据定理2.1(或者定理2.2),可得上述n=3的时滞FCNNs(1)是MSE-ISS的,并且指数收敛率为1.17.

致谢重庆邮电大学博士启动基金(A2016-80)和重庆邮电大学大学生科研训练计划项目(A2017-71)对本文给予了资助，谨致谢意.