关于不定方程x2-5y4=236
刘 杰
(三明医学科技职业学院人文教育学院,福建 三明 365000)
关于不定方程x2-Dy4=C(其中D,C为给定的整数,且D〉0为非平方数)曾有多人研究。设N(D,C)为方程x2-Dy4=C的正整数解的组数,文献[1]证明了以下几个结果:N(5,44)=1,(x,y)=(7,1);N(5,11)=2,(x,y)=(4,1)和(56,5);N(5,-44)=3,(x,y)=(6,2),(19,3)和(181,9)。文献[2-4]证明了在y≡0(mod8)时,N(2,17)=0,N(2,41)=0,N(8,17)=0,N(2,97)=0。 文献[5-7]证明了 N(3,97)=1,(x,y)= (10,1)。 文献[8]证明了 N(3,397)=1,(x,y)=(20,1)。
本文利用递推序列、同余式和平方剩余的方法证明了不定方程x2-5y4=236仅有正整数解(x,y)=(271,11)。
1.定理及证明

仅有正整数解(x,y)=(271,11) 。
证明:首先考虑方程 x2-5y2=236,其全部整数解由以下6个结合类给出:


1.1 讨论结合类(2)(3)
因为两个结合类±(Xn+Yn)和±()是共轭的,而Yn=Y-n,
由于(Un+Yn)=(9+4)n,所以如果(1)式有解则应满足 y2=±(2Un+16Vn)(n∈Z)或 y2=±(2Un-16Vn)(n∈Z)。 但当 n≥0 时,2Un+16Vn〉0,n〈0 时,2Un+16Vn〈0;n〉0 时,2Un-16Vn〈0,n≤0 时,2Un-16Vn〉0。
因此(1)式的解可归结为:(ⅰ)Yn=y2=2Un+16Vn(n≥0)或 (ⅱ)Yn=y2=-2Un+16Vn(n〉0)
亦即只要证明 Yn=2Un+16Vn或 Yn=-2Un+16Vn是否是一个完全平方数。
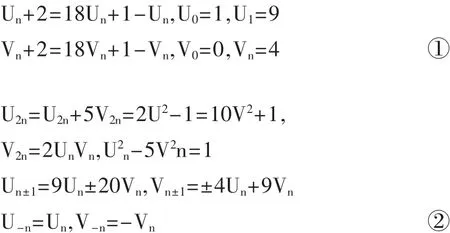
可以验证以下3组关系式成立:Un+2km≡(-1)kUn(modUm),Vn+2km≡(-1)kVn(modUm) ③
情形(ⅰ)Yn=2Un+16Vn(n≥0)
由关系式①对{Yn}取模3得剩余类序列周期为 4,当 n≡0,3(mod4)时 Yn≡2(mod3),因为(2/3)=-1(其中(a/p)表示 jacobi符号),所以 Yn不可能是一个平方数,从而使Yn=y2=2Un+16Vn无整数解,以下排除的数都是据计算 (a/p)=-1得出Yn不可能是一个平方数,从而使y无解。剩n≡1,2(mod4)等价于 n≡1,2,5,6(mod8)。 取模 7得剩余类序列周期为 8,当 n≡1,6(mod8)时 Yn≡5,3(mod7)使Yn不是一个平方数。
取模23得剩余类序列周期为8,当n≡5(mod8)时,Yn≡10(mod23)使 Yn不是一个平方数。剩 n≡2(mod8)等价于 n≡2,10(mod16),取模 1103得剩余类序列周期为 16,当 n≡2(mod16)时,Yn≡371(mod1103)使 Yn不是一个平方数,取模 47得剩余类序列周期为 16,当 n≡10(mod16)时,Yn≡30(mod47)使Yn不是一个平方数。所以此情形对所有n都使Yn不是一个平方数,从而y无解。
情形(ⅱ)Yn=y2=-2Un+16Vn(n〉0)
对 {Yn}取模3得剩余类序列周期为 4,当n≡2,3(mod4)时 Yn≡2(mod3),因 为 (2/3)=-1(其中(a/p)表示 jacobi符号),所以 Yn不可能是一个平方数,从而使Yn=y2=-2Un+16Vn无整数解。剩n≡0,1(mod4)等价于 n≡0,1,4,5(mod8),取模 7 得剩余类序列周期为 8,当 n≡0,5(mod8)时,Yn≡5,3(mod7)使 Yn不是一个平方数。剩 n≡1,4(mod8)等价于 n≡1,4,9,12(mod16),取模 47得剩余类序列周期为 16,当 n≡1,4(mod16)时,Yn≡46,20(mod47),取模1103得剩余类序列周期为16,当 n≡9(mod16)时 Yn≡1057(mod1103)使 Yn不是一个平方数。剩 n≡12(mod16)等价于 n≡12,28(mod32),取模3167得剩余类序列周期为 32,当n≡12(mod32)时,Yn≡2743(mod3167)使 Yn不 是按个平方数。取模2207得剩余类序列周期为32,当n≡28(mod32)时,Yn≡2086(mod2207)使 Yn不是一个平方数。由以上所证此情形对所有n都使Yn不是一个平方数,从而y无解。
1.2 讨论结合类(4)(5)
如果(1)式有解则应满足 y2=±(5Un+19Vn)(n∈Z)或 y2=±(5Un-19Vn)(n∈Z), 但当 n≥0时,5Un+19Vn〉0,n〈0 时 5Un+19Vn〈0;n〉0 时 5Un-19Vn〈0,n≤0 时,5Un-19Vn〉0,
因此 (1)式的解可归结为:(ⅰ)Yn=y2=5Un+19Vn(n≥0)或(ⅱ)Yn=y2=-5Un+19Vn(n〉0)。
情形(ⅰ)Yn=5Un+19Vn(n≥0)
由关系式①对 {Yn}取模3得剩余类序列周期为 4,当 n≡0,3(mod4)时,Yn≡2(mod3),得出 Yn不可能是一个平方数,从而使y无解。剩n≡1,2(mod4)等价于 n≡1,2,5,6,9,10(mod12)。 取模 17得剩余类序列周期为 12,当n≡2,6,9(mod12)时,Yn≡14,5,12(mod17),取模107得剩余类序列周期为 12,当 n≡5(mod12)时,Yn≡31(mod107)使 Yn不是一个平方数。剩下n≡1,10(mod12),等价于n≡1,10,13,22(mod24)。取模7得剩余类序列周期为24,当 n ≡10,13(mod24)时 ,Yn≡3,5(mod7), 取 模103681得剩余类序列周期为24, 当n≡22(mod24)时 ,Yn≡103118(mod103681)使 Yn不 是 一个平方数,从而剩下n≡1(mod24)。
又由前剩n≡1,2(mod4)等价于n≡1,2,5,6,9,10,13,14,17,18(mod20)。取模41得剩余类序列周期为 20,当 n≡6,17,18(mod20)时有 Yn≡30,11,24(mod41),取模2521得剩余类序列周期为20,当n≡2,13,14(mod20)时有 Yn≡2173,1343,1137(mod2521),取模61得剩余类序列周期为20,当n≡9(mod20)时有Yn≡30(mod61)使Yn不是一个平方数。剩下n≡1,5,10(mod20)等价于 n≡1,5,10,21,25,30(mod40)。取模 7得剩余类序列周期为 40,当n≡5(mod40)时有 Yn≡5(mod7),取模 23得剩余类序列周期为 40,当 n≡10,21(mod40)时有 Yn≡11,17(mod23),取模 241得剩余类序列周期为40,当 n≡25(mod40)时有 Yn≡234(mod241)使 Yn不是一个平方数。剩下n≡1,30(mod40)等价于n≡1,30,41,70(mod80)。取模47得剩余类序列周期为80,当 n≡41,70(mod80)时有 Yn≡20,46(mod47),取模1103得剩余类序列周期为80,当n≡30(mod80)时有 Yn≡540(mod1103),使 Yn不是一个平方数。剩下n≡1(mod80)结合前面 n≡1(mod24)则n≡1(mod120)才使Yn可能是一个平方数。
当 n≡1(mod120),x≠1 时,设 n=1+2×3×5×2t×k(k≡1(mod2),t≥2)
令 m=15×2t,由关系式②、③

k≡3(mod4)时

由于 U2m≡1(mod8),设 2s|Vm,则

对U2m取模271,得剩余类序列周期为45。按m的取法 2m≡15,30(mod45),此时有 U2m≡135(mod271)。 由于(135/271)=-1 与(y2/U2m)=1 矛盾,所以这时Yn不是一个平方数,使y2=5Un+19Vn无解。当n=1时,得到y=11,从而得(1)式的一组正整数解(x,y)=(271,11)。
情形(ⅱ)Yn=-5Un+19Vn(n〉0)
对{Yn}取模3得剩余类序列周期为4,当n≡2,3(mod4)时,Yn≡2(mod3),Yn不可能是一个平方数,从而使Yn=y2=-2Un+16Vn无整数解。剩n≡0,1(mod4)等价于 n≡0,1,4,5(mod8),取模 7得剩余类序列周期为 8,当 n≡1(mod8)时,Yn≡3(mod7),取模23得剩余类序列周期为 8,当 n≡4,5(mod8)时,Yn≡5,15(mod23)。 剩 n≡0(mod8)等价于 n≡0,8(mod16),取模7得剩余类序列周期为8,当n≡1(mod8)时,Yn≡3(mod7),取模23得剩余类序列周期为8,当n≡4,5(mod8)时,Yn≡5,15(mod23),所以此情形对所有的n均使Yn不是一个平方数,从而y无解。
1.3 讨论结合类(6)(7)
如果(1)式有解则应满足 y2=±(11Un+29Vn)(n∈Z)或 y2=±(11Un-29Vn)(n∈Z)。 但当 n≥0 时,11Un+29Vn〉0,n〈0 时 11Un+29Vn〈0;n〉0 时 11Un-29Vn〈0,n≤0 时,11Un-29Vn〉0。
因此 (1)式的解可归结为:(ⅰ)Yn=y2=11Un+29Vn(n≥0)或(ⅱ)Yn=y2=-11Un+29Vn(n〉0)
情形(ⅰ)Yn=11Un+29Vn(n≥0)
对{Yn}取模8得剩余类序列周期为2,当n≡0,1(mod2)时,Yn≡3,7(mod8),为模 8 的平方非剩余。故此情形无解。
情形(ⅱ)Yn=y2=-11Un+29Vn(n〉0)
对{Yn}取模8得剩余类序列周期为4,当n≡0,2(mod4)时,Yn≡5(mod8),为模 8的平方非剩余。取模3得剩余类序列周期为4,当n≡1(mod4)时,Yn≡2(mod3),为模 3的平方非剩余,剩下 n≡3(mod4),等价于n≡3,7(mod8)。取模7得剩余类序列周期为 8,当 n≡3(mod8)时,Yn≡5(mod7)。 取模 23得剩余类序列周期为 8,当 n≡7(mod8)时,Yn≡15(mod23),此情形对所有的n均使Yn不是一个平方数,从而y无解。
通过以上的讨论知(1)式只有正整数解(x,y)=(271,11),证毕。

