基于K-阶结构熵的网络异构性研究∗

黄丽亚 霍宥良 王青 成谢锋

(南京邮电大学,电子与光学工程学院,微电子学院,南京 210023)

(2018年7月19日收到;2018年11月8日收到修改稿)

结构熵可以考察复杂网络的异构性.为了弥补传统结构熵在综合刻画网络全局以及局部特性能力上的不足,本文依据网络节点在K步内可达的节点总数定义了K-阶结构熵,可从结构熵随K值的变化规律、最大K值下的结构熵以及网络能够达到的最小结构熵三个方面来评价网络的异构性.利用K-阶结构熵对规则网络、随机网络、Watts-Strogatz小世界网络、Barabási-Albert无标度网络以及星型网络进行了理论研究与仿真实验,结果表明上述网络的异构性依次增强.其中K-阶结构熵能够较好地依据小世界属性来刻画小世界网络的异构性,且对星型网络异构性随其规模演化规律的解释也更为合理.此外,K-阶结构熵认为在规则结构外新增孤立节点的网络的异构性弱于未添加孤立节点的规则结构,但强于同节点数的规则网络.本文利用美国西部电网进一步论证了K-阶结构熵的有效性.

1 引 言

大量系统都可以使用复杂网络进行抽象的表达[1].复杂网络各部分之间虽相互联系,但通常存在着功能结构上的差异[2,3].因此,对网络异构性的研究是分析节点重要性排序[4,5]、社区结构划分[6,7]以及网络传播效率、同步能力等[8,9]内容的重要基础.通常,网络异构性是从拓扑结构的角度出发,通过定义结构熵予以定量评价.结构熵越小,意味着网络各部分间的差异越大,异构性越强;反之意味着网络结构越趋于均衡,异构性越弱.目前,已有诸多研究[10-15]各自从不同的角度定义了网络结构熵.

Wu熵[10]以节点为主体,试图通过分析网络节点所拥有的边的条数,即各节点度值之间的差异来反映网络的异构性.而度分布结构熵[11](下文简称DD熵)则以度值为主体,依据拥有不同度值的节点数量之间的差异,对网络的异构性进行了刻画.可见,以上两种方法仅将邻居节点纳入评价体系,未考虑非邻居节点的影响,因而刻画网络全局特性的能力较弱,且对“桥”连接节点的重视程度不足.此外,Wu熵难以充分地解释网络中出现孤立节点的情况.蔡萌等[12]提出了一种基于点和边差异性的网络结构熵(下文简称SD熵),虽然将“点差异性”与“边差异性”进行加权求和,但其本质仍是从网络局部特性的角度出发,且加权系数是人为设置的,结果较为主观;此外,SD熵在计算节点相对重要性时,人为地引入了∆项,缺少理论解释.为了充分利用网络的全局特性,文献[13,14]以节点介数以及边介数为判据,定量地评价了网络的异构性(下文简称节点介数熵为NB熵;边介数熵为EB熵).介数虽然突出了桥节点的重要性,但对网络拓扑中包含有环型或星型结构的部分解释不足.为了综合评估网络的局部以及全局特性,蔡萌等[15]又提出了一种基于最大流的网络结构熵,该方法使用网络流量变化和节点度值的加权平均来计算网络的异构性,但仍存在权重的选择较为主观、对∆项的解释不足等问题;且当网络规模较大时,最大流矩阵的计算也十分复杂.此外,若网络流量变化与节点度值量级不同,最终结果易受量级较大部分的影响.因此,寻找一种能够综合考查网络全局以及局部特性的方便有效的异构性评价方法是本研究的目的所在.

文献[16,17]将网络视为节点间相互作用的系统,每个节点均处于其他所有节点产生的势场之中.该方法假设网络拓扑为短程场,并基于高斯势函数定义了网络拓扑势函数,通过比较各个节点所处位置势场值的大小研究了节点重要性、社区划分等网络特性.但网络势程的长短以及势函数的形式应依网络所代表的实际意义而各有不同,短程场以及高斯势函数的假设均具有一定的局限性.

本研究试图摒弃势程长短、势函数等额外假设,仅利用网络的结构特性提出了一种K-阶结构熵模型,并对规则网络、随机网络、WS(Watts-Strogatz)小世界网络、BA(Barabási-Albert)无标度网络、星型网络、在规则结构外新增孤立节点的网络以及美国西部电网进行了理论研究与仿真分析,以证明该结构熵可以较好地反映不同网络的异构性.

2 K-阶结构熵模型

首先给定无权无向网络图G(V,E),其中V={v1,v2,···,vn}为节点集,共n个节点,E为边集,并假设lij为节点vi到vj的最短路径长度.为了避免网络有无自环在分析上造成的差异,本文假设节点0步即可到达该节点本身,定义节点的K-阶邻居数为

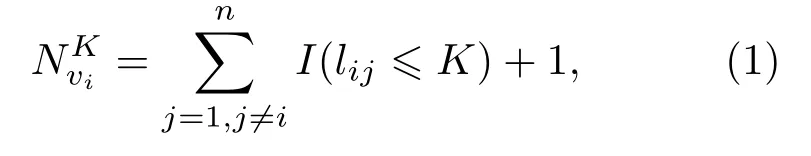
其中I(·)为指示函数,即当节点vi与vj之间的最短路径长度lij6K时I(·)=1,否则I(·)=0. 由(1)式可知,对于任意节点有=1.

K-阶邻居数衡量了网络节点在K步内可达的节点总数,本文将K值命名为影响力尺度.由于本文研究的网络大小是有限的,显然当K大于网络最大连通部分的直径d时,各节点的K-阶邻居数均不再随K值的变化而变化.因此K∈{0,1,···,d},并将d命名为最大影响力尺度.

若某节点的K-阶邻居数越多,可认为该节点在尺度K下所影响的节点越多,节点则越重要.为了衡量网络在尺度K下各节点影响力或重要性的差异,即网络的异构性,可将所有节点的K-阶邻居数加总代入到信息熵公式,从而得到K-阶结构熵为

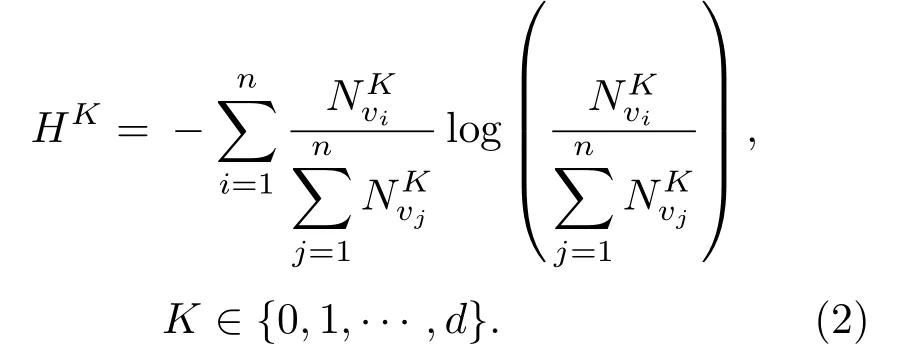
由随机矩阵理论可知,网络邻接矩阵A的k次幂Ak中的第i行、第j列元素表示从节点vi到vj通过k条边连接的路径数目.因此,(1)式可以改写为

其中为矩阵Ak中的第i行、第j列元素.此处A0=E为单位阵,恰对应于前文节点零步可达该节点自身这一假设.

事实上,(3)式表示的是矩阵多项式A0+A1+中第i行或列向量(无向图的邻接矩阵A为对称阵,则其多项式亦对称)中非零元素的个数,即L0范数.于是(3)式可以改写为

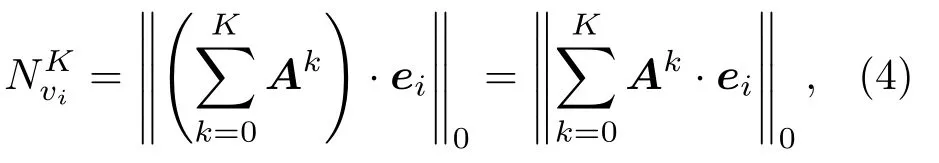
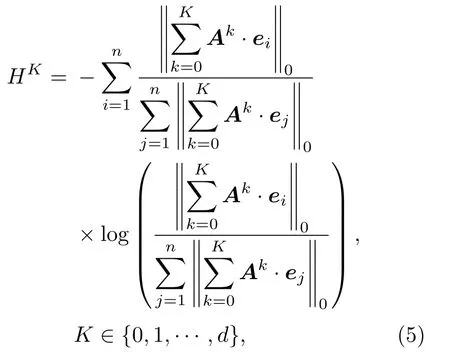
HK值越小,证明网络在影响力尺度K下的异构性越强,反之越弱.

由前文可知,K的取值是有限的,因此在分析网络异构性时仅需研究K-阶结构熵序列{H0,H1,···,Hd}即可. 对任意网络而言, 当K=0时,各节点0步内只可到达其本身,因此有H0=log(n);当K=1时,各节点1步内可达该节点本身及其邻居节点,因此H1按各节点“度值加一”代入信息熵公式进行计算,与Wu熵相似却存在差异.若网络是连通的,各节点在d步内均可到达网络任意节点,因此Hd=log(n);若网络是非连通的,Hd将依网络结构而各不相同.此外,由于结构熵序列是可列有限的,其最小值minH=min{H0,H1,···,Hd}可被认为表征了网络能够达到的最强异构性.综上所述,在应用K-阶结构熵模型研究网络的异构性时,应综合考察结构熵序列随K值的变化规律、Hd以及minH.

当网络为有向网络时,可将上述K-阶结构熵演变为K-阶发送以及接收结构熵两部分进行讨论.此时,可以将由某节点出发、K步内可达的节点总数(包含其自身)记为该节点的K-阶发送节点数,依此得到K-阶发送结构熵;同理可以计算出K-阶接收结构熵.显然,K-阶发送以及接收结构熵分别衡量了网络发、收能力的异构性,分析时均应予以考虑.当网络为有权网络时,若网络边权表示节点间的路径长度,在计算节点的K-阶邻居数时,只需按有权网络路径长度的方法进行计算即可;若网络权值表示节点间连接的强度时,则可选定某一阈值或者采用多阈值的方法将网络进行二值化处理,再利用上述方法进行研究.

3 典型网络的结构熵

为了验证K-阶结构熵评价网络异构性的能力,本文对规则网络、随机网络、WS小世界网络、BA无标度网络、星型网络、在规则结构外新增孤立节点的网络以及美国西部电网进行了仿真分析.以下所有仿真结果均取500次实验的平均值.

3.1 WS小世界网络

小世界网络是指具有较大平均聚类系数以及较短特征路径长度的一类网络结构.Watts与Strogatz[18]最先提出了一种构造小世界网络的方法,即将最近邻耦合网络每条边的一个端点保持不变,另外一个端点依概率p随机改连至其他节点,通常将生成的网络称为WS小世界网络.当p=0时,网络为规则结构,其异构性应当最弱;当p=1时,网络中任意两节点依一定概率随机连接,其网络异构性应强于规则网络.值得注意的是,WS小世界网络虽为规则与随机网络之间的过渡形式,其“主体”保持着最近邻耦合结构,而个别节点却拥有“长程”连接.但正是由于这些特殊节点的存在,使得网络的特征路径长度大大减少,起到了“桥”的作用.由此可见,WS小世界网络中个别节点存在着连接上的突出优势,而随机网络各节点的连接状态是相似的,因此可认为WS小世界网络的异构性强于随机网络.

下面基于K-阶结构熵模型从结构熵随K值的变化规律、网络最强异构性minH等角度对WS小世界网络进行考察.本文约定网络随机重连后不能有自环、重边且仍为连通图,易证Hd=H0=log(n).接下来,图1和图2分别仿真了50和200节点最近邻耦合网络在不同重连概率p下所生成网络的结构熵随K值的变化规律,其中该最近邻耦合网络每个节点与其左右各2个邻居节点相连.

显然,最近邻耦合网络的结构是对称的,节点数为n的最近邻耦合网络的K-阶结构熵恒等于log(n),如图1(a)和图2(a)所示.由于随机重连打破了网络结构的对称性,在50及200节点网络中均可观察到,在任意重连概率p下,网络结构熵随K值的增加先下降再上升,且结构熵最小值minH所对应的K值随p的增大而逐渐减小.但值得注意的是,当节点个数为50时,minH随p的增加而减小;但当节点个数为200时,minH随p的增加先减小,如图2(a)—(f),后又略有增大,如图2(f)—(h).有理由认为,minH不仅与网络的拓扑结构有关,更与网络的规模有着密切的联系.因此,图3仿真了网络minH与小世界指数σ随网络节点数n以及重连概率p的变化曲线,其中对minH进行了归一化处理.参照有关文献[19,20],本文所使用的小世界指数定义为

其中,C和L分别为网络的平均聚类系数与特征路径长度,Cn与Ln分别为同节点数最近邻耦合网络的平均聚类系数与特征路径长度.显然,当网络为最近邻耦合网络时,σ=1;由于小世界网络拥有较高的平均聚类系数,与最近邻耦合网络相近,即C≈Cn;但其特征路径长度较短,远小于最近邻耦合网络,与同规模随机网络相近,即L≪Ln.因此可认为σ值越大,网络的小世界性越显著;由图3所示,从某p值开始,σ随p的增加而下降.这是由于随着重连概率的增加,网络将同时具有较短的特征路径长度以及较小的平均聚类系数,逐渐呈现出随机网络的特性.

图1 50节点最近邻耦合网络在不同重连概率p及影响力尺度K下的结构熵 (a)p=0;(b)p=0.001;(c)p=0.002;(d)p=0.005;(e)p=0.01;(f)p=0.05;(g)p=0.1;(h)p=0.5;(i)p=1Fig.1.K-order structure entropy at in fluence scale K in graphs generated by randomly rewiring a 50 nodes nearest-neighbor coupled network based on different probability p:(a)p=0;(b)p=0.001;(c)p=0.002;(d)p=0.005;(e)p=0.01;(f)p=0.05;(g)p=0.1;(h)p=0.5;(i)p=1.

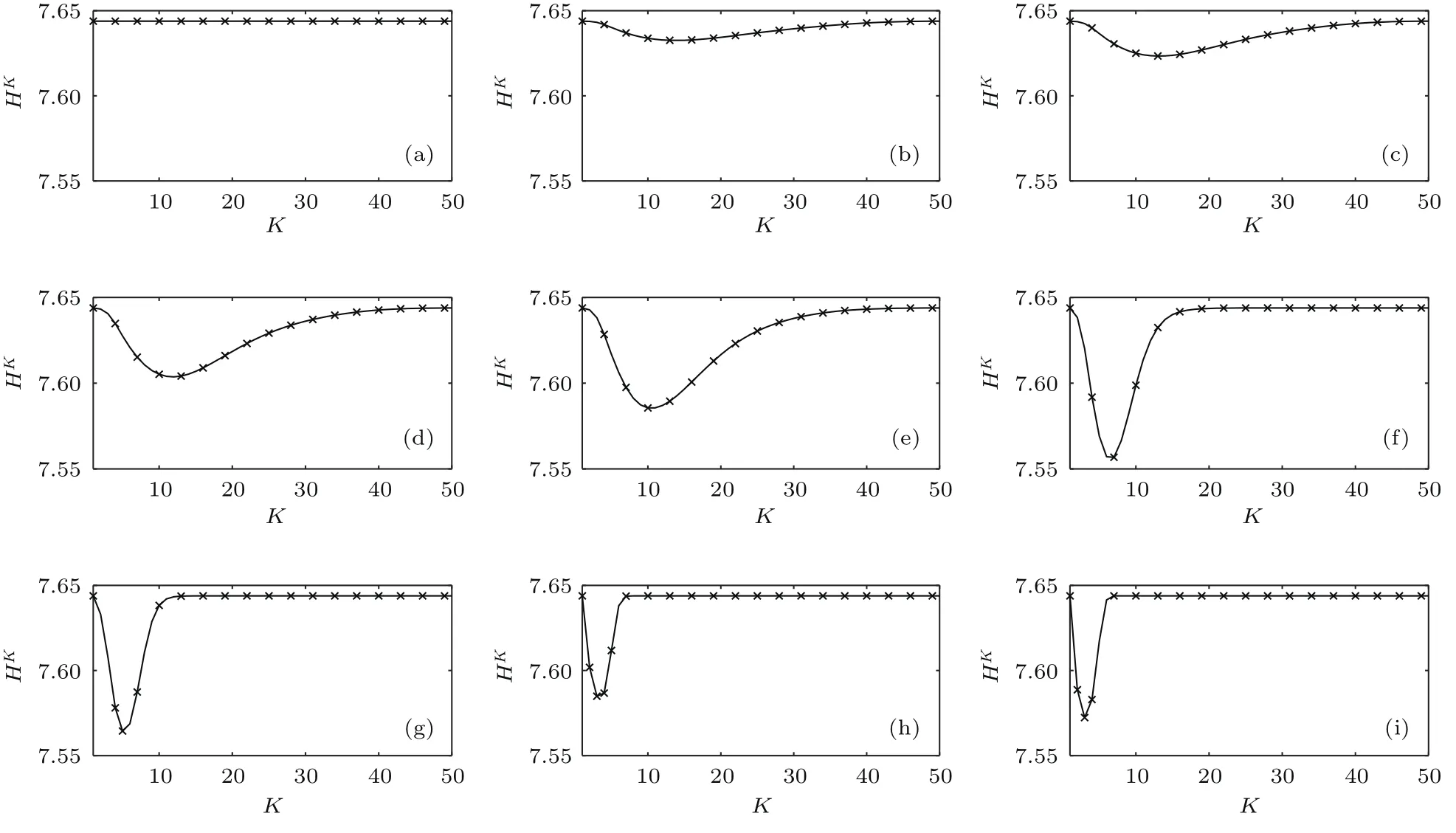
图2 200节点最近邻耦合网络在不同重连概率p及影响力尺度K下的结构熵 (a)p=0;(b)p=0.001;(c)p=0.002;(d)p=0.005;(e)p=0.01;(f)p=0.05;(g)p=0.1;(h)p=0.5;(i)p=1Fig.2.K-order structure entropy at in fluence scale K in graphs generated by randomly rewiring a 200 nodes nearestneighbor coupled network based on different probability p:(a)p=0;(b)p=0.001;(c)p=0.002;(d)p=0.005;(e)p=0.01;(f)p=0.05;(g)p=0.1;(h)p=0.5;(i)p=1.

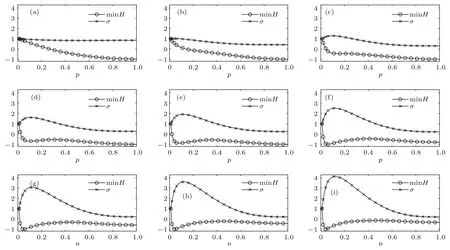
图3 不同网络规模n及重连概率p下的minH和小世界指数σ (a)n=10;(b)n=25;(c)n=50;(d)n=75;(e)n=100;(f)n=150;(g)n=200;(h)n=250;(i)n=300Fig.3.The minimum structure entropy minH and small-world coefficient σ at different network size n and rewiring probability p:(a)n=10;(b)n=25;(c)n=50;(d)n=75;(e)n=100;(f)n=150;(g)n=200;(h)n=250;(i)n=300.

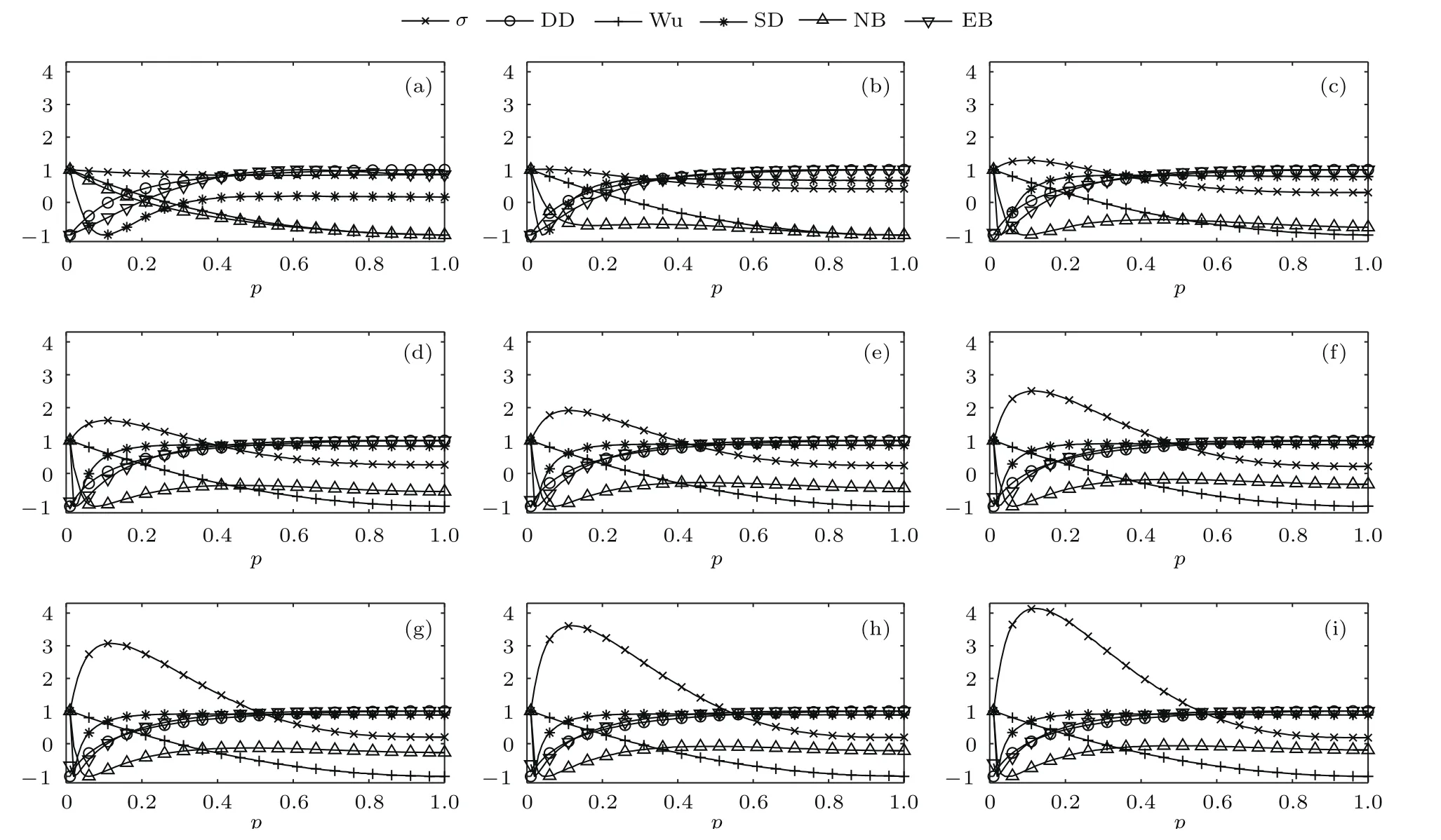
图4 不同网络规模n及重连概率p下的小世界指数σ,DD熵、Wu熵、SD熵、NB熵以及EB熵 (a)n=10;(b)n=25;(c)n=50;(d)n=75;(e)n=100;(f)n=150;(g)n=200;(h)n=250;(i)n=300Fig.4.Small-world coefficientσ,degree distribution entropy(DD entropy),Wu entropy(Wu entropy),node and edge difference entropy(SD entropy),node betweenness entropy(NB entropy),edge betweenness entropy(EB entropy)at different network size n and rewiring probability p:(a)n=10;(b)n=25;(c)n=50;(d)n=75;(e)n=100;(f)n=150;(g)n=200;(h)n=250;(i)n=300.

由图3可知,当网络规模较小时,网络的小世界性不明显,minH随p的增加单调下降;当网络规模较大且p较小时,网络具有显著的小世界性,此时minH随重连概率先下降再上升.因此,K-阶结构熵认为最近邻耦合网络、随机网络以及WS小世界网络的异构性依次增强,且网络的小世界性越强,其异构性则越强.可见,K-阶结构熵模型能够较好地依据小世界属性来反映网络的异构性.

为了进一步验证K-阶结构熵的性能,图4绘制了小世界指数σ与DD熵、Wu熵、SD熵、NB熵以及EB熵随网络节点数n以及重连概率p的变化曲线.

由图4可见,在任意网络规模下,DD熵随p单调递增,而Wu熵随p单调递减,可见DD熵与Wu熵均难以表征小世界网络的异构性;此外,DD熵认为随机网络的异构性弱于规则网络,与通常理解存在偏差;当网络规模较小时,SD熵认为最近邻耦合网络、随机网络以及WS小世界网络的异构性依次增强,与本文结论相似.但当网络规模较大时,SD熵随p的增加迅速上升,随之保持在随机网络的异构性水平不变,但此时网络仍具有较强的小世界性;EB熵在网络小世界性较强时认为WS小世界网络的异构性最强,但却认为随机网络的异构性弱于最近邻耦合网络,这一结论同样与普遍理解存在偏差.只有NB熵与本文结论相似.

3.2 BA无标度网络与星型网络

BA无标度网络依据增长和择优机理而构建[21],所生成的网络度分布符合γ=3的幂律形式,网络中少数节点拥有极多的连接,而大多数节点只有少量的连接,通常认为无标度网络具有较强的异构性[22,23].星型网络是指以中央节点为中心,其余节点均只与中央节点相连的拓扑结构,通常可被看作是无标度网络的极端形式,其异构性要强于一般的无标度网络.下面基于K-阶结构熵对二者的异构性进行考察.文中规定BA无标度网络与星型网络均为连通图,同样有Hd=H0=log(n).

图5仿真了在不同网络规模下,BA无标度网络与星型网络归一化后的K-阶结构熵随K的变化规律.

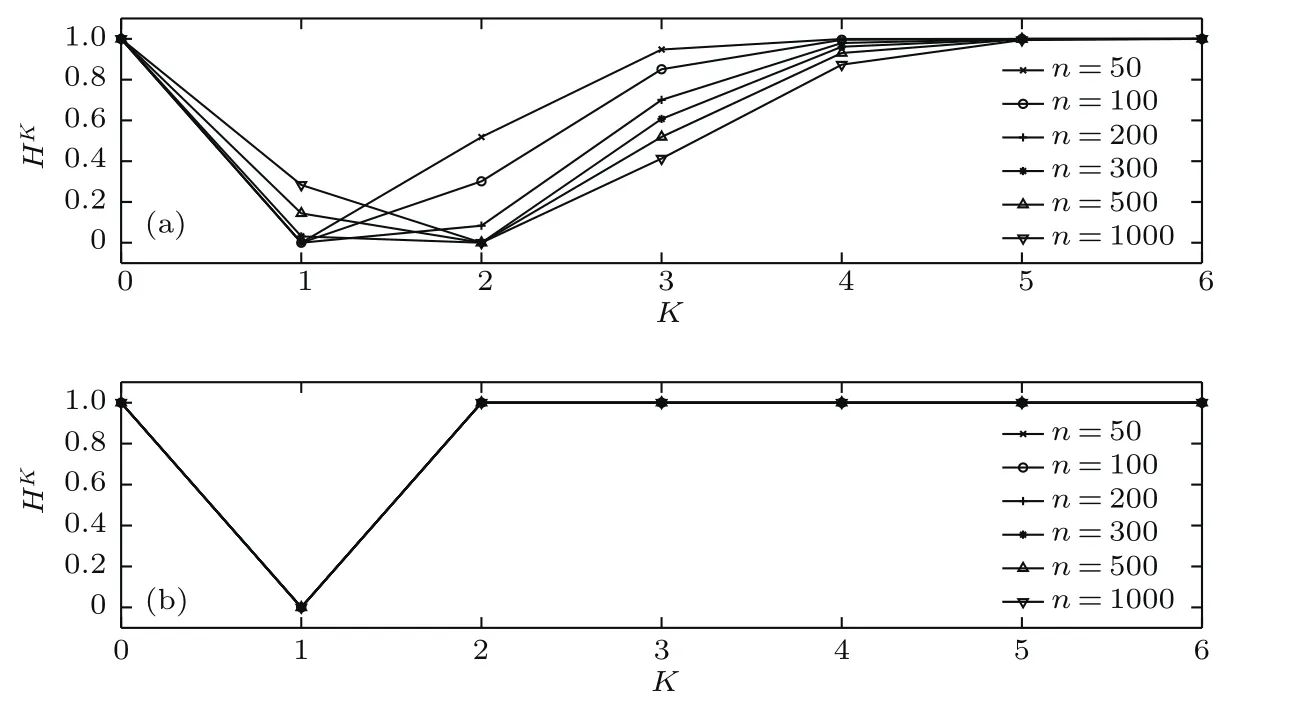
图5 BA无标度网络及星型网络在不同网络规模n及影响力尺度K下的结构熵 (a)BA无标度网络;(b)星型网络Fig.5.K-order structure entropy of BA scale-free networks and star networks at different in fluence scale K and the network size n:(a)BA scale-free network;(b)star network.

由图5可见,在任意网络规模下,BA无标度网络与星型网络的结构熵均随K的增加先下降再上升.此外,BA无标度网络minH所对应的K值随网络规模的增加逐渐增大,而星型网络minH所对应的K值与网络规模无关,即K=1时达到最小.这是由于在任意网络规模下,星型网络的节点均可在二步内到达其余节点.图6仿真了最近邻耦合网络、随机网络、BA无标度网络以及星型网络等不同结构的minH,DD熵、Wu熵、SD熵、NB熵和EB熵随网络节点数n的变化情况.

由图6可见,minH与Wu熵认为,在任意网络规模下,最近邻耦合网络、随机网络、BA无标度网络以及星型网络的异构性依次增强;且随着网络规模的增加,以上拓扑结构的minH与Wu熵均呈上升趋势.在此观点下,星型网络的异构性随网络规模的增加而减弱,这可以解释为在任意网络规模下,星型网络只拥有一个中心节点,其余节点均是度1节点.随着网络规模的增加,重要性相同的度1节点的数量显著增加,这导致了网络的异构性有所减弱.此结论比SD熵和DD熵认为的星型网络的异构性随其规模的增大略有增强后保持不变的解释更为合理;此外,DD熵区分随机网络与BA无标度网络的能力不足,且无法充分反映最近邻耦合网络异构性随其网络规模的演化规律;NB熵对最近邻耦合网络、随机网络以及BA无标度网络异构性随其网络规模演化规律的解释与K-阶结构熵相同,但却无法充分反映星型网络的异构性;EB熵认为随机网络与BA无标度网络的异构性弱于最近邻耦合网络,与通常解释存在偏差.

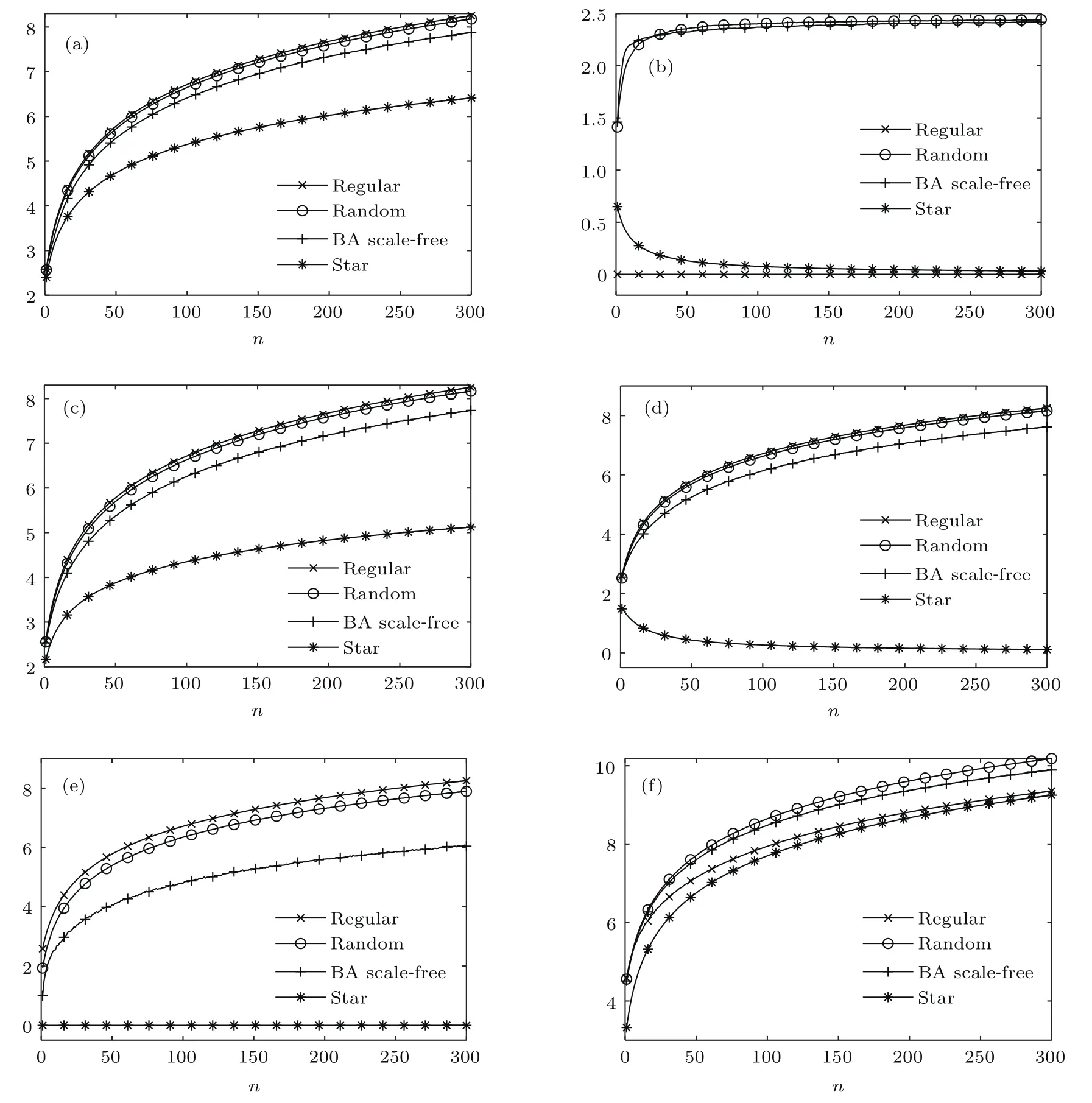
图6 最近邻耦合网络、随机网络、BA无标度网络、星型网络在不同网络规模n下的minH,DD熵、Wu熵、SD熵、NB熵以及EB熵 (a)minH;(b)DD熵;(c)Wu熵;(d)SD熵;(e)NB熵;(f)EB熵Fig.6.The minH,DD entropy,Wu entropy,SD entropy,NB entropy,EB entropy of nearest-neighbor coupled networks,random networks,BA scale-free networks and star networks at different network size n:(a)minH;(b)DD entropy;(c)Wu entropy;(d)SD entropy;(e)NB entropy;(f)EB entropy.

3.3 在规则结构外新增孤立节点的网络

由于最近邻耦合网络、全连接网络和环型网络等规则网络的结构是对称的,因此其异构性应当较弱.现假设在规则网络结构之外再新增若干个孤立节点,由于孤立节点在网络中的结构与作用是固定不变的,它们只影响其自身,不与原规则部分中的任何节点发生作用,即孤立节点的存在增加了网络的无序程度,因此该网络的异构性应弱于原规则结构;但由于孤立节点与原规则部分的节点存在着结构上的差异,因此在规则结构外新增孤立节点的网络的异构性应强于同节点数的规则网络.

不失一般性,以下内容以最近邻耦合网络为例进行分析.由前文可知,当最近邻耦合网络未新增孤立节点时,K-阶结构熵在任意影响力尺度K下均为log(n);现假设最近邻耦合网络的节点数为n,额外新增的孤立节点数为i,在任意影响力尺度K下,易证原最近邻耦合部分各节点的K-阶邻居数相同,记为

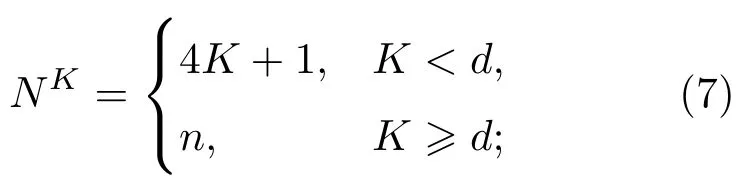
而各孤立节点的K阶邻居数始终为1.因此,得到该网络结构的K-阶结构熵为

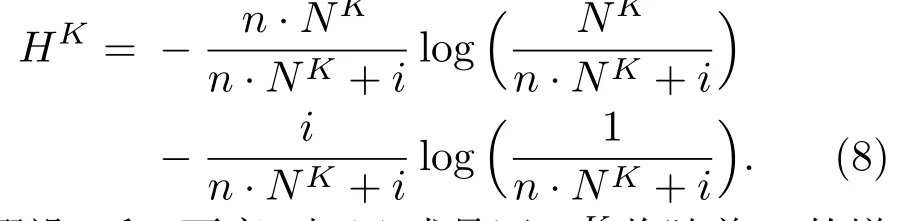
若假设n和i不变,由(8)式易证HK将随着K的增加单调减少,因此有Hd6H0,即Hd6 log(n+i);且最大影响力尺度d下的结构熵Hd与最小结构熵minH相等.在最大影响力尺度d下,对于原最近邻耦合网络部分的节点有Nd=n,因此网络的Hd即minH为

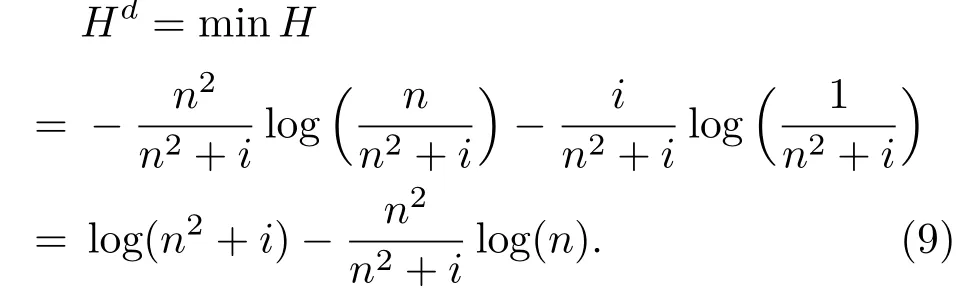
由(9)式易证log(n)6Hd.综上有log(n)6Hd6 log(n+i),即可认为在n节点最近邻耦合网络外新增i个孤立节点后,其网络异构性介于n与n+i节点最近邻耦合网络之间,与前文讨论相符.事实上,节点为n的任意连通图额外新增i个孤立节点后,其最大影响力尺度d下的异构性Hd均符合(9)式的结果,但网络最小结构熵minH未必等于Hd.此外,随着孤立节点的增多,当i≫n2时,(9)式可近似为log(i),这可认为当孤立节点的数量远超原网络(任意连通图)的规模时,其网络异构性将更多地受到孤立节点的影响,也是符合实际的.值得注意的是,任意连通图的Hd始终为log(n).因此只有当网络非连通时,Hd的讨论才有意义.

图7 在20节点最近邻耦合网络外新增i个孤立节点后的网络在不同K值下的结构熵Fig.7.K-order structure entropy at different in fluence scale K of different networks generated by adding isolated nodes to a 20 nodes nearest-neighbor coupled network,where the number of isolated nodes is i.

图7 仿真了20节点最近邻耦合网络新增i个孤立节点后,其K-阶结构熵随K值的变化规律.图8则绘制了20节点最近邻耦合网络新增i个孤立节点后,其Hd(minH),DD熵、Wu熵、SD熵、NB熵以及EB熵随i的变化规律.

如图8所示,Wu熵、SD熵、NB熵以及EB熵均认为n节点最近邻耦合网络新增i个孤立节点后,其网络异构性要强于n+i节点最近邻耦合网络;但Wu熵、NB熵以及EB熵却认为n节点最近邻耦合网络增添孤立节点前后的网络异构性不发生变化,这一结论忽略了孤立节点对网络结构的影响;而SD熵认为与原n节点最近邻耦合网络相比,网络异构性随增添孤立节点个数的增加先增大后减少,目前对于这一结论缺乏合理的解释;DD熵认为n节点最近邻耦合网络增添i个孤立节点后,其网络异构性要比n和n+i节点最近邻耦合网络都弱,与前文讨论不一致.由此可见,K-阶结构熵对最近邻耦合网络新增孤立节点后的网络异构性的解释更为合理.其实,K-阶结构熵与Wu熵类似,均将节点作为基本单元来评价网络的异构性,但本文将节点自身纳入影响力范围,从而避免了Wu熵中由于孤立节点度值为0所造成的分析上的不便.

综上所述,K-阶结构熵能够较好地刻画并区分规则网络、随机网络、WS小世界网络、BA无标度网络以及星型网络的异构性,认为以上网络的异构性依次增强,与文献[24]的理论研究保持一致.其中,K-阶结构熵能够较好地依据小世界属性来刻画WS小世界网络的异构性,且对星型网络异构性随其规模演化规律的解释也更为合理.此外,本文还分析了在规则结构外新增孤立节点后的网络的异构性,认为n节点规则网络增添i个孤立节点后,其异构性介于n和n+i节点规则网络之间,并初步探索了minH和Hd之间的关系.

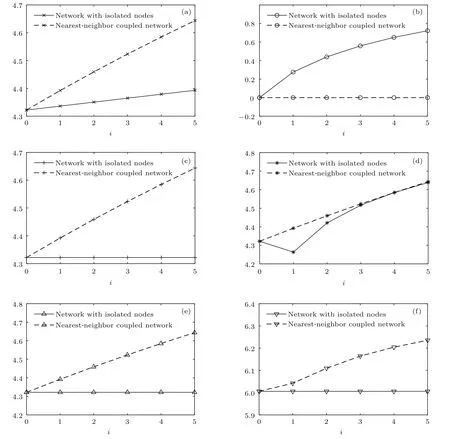
图8 在20节点最近邻耦合网络外新增i个孤立节点后的网络与20+i节点最近邻耦合网络的Hd(minH),DD熵、Wu熵、SD熵、NB熵以及EB熵 (a)Hd(minH);(b)DD熵;(c)Wu熵;(d)SD熵;(e)NB熵;(f)EB熵Fig.8.The Hd(minH),DD entropy,Wu entropy,SD entropy,NB entropy,EB entropy of(20+i)nodes nearestneighbor coupled networks and graphs generated by adding i isolated nodes to 20 nodes nearest-neighbor coupled networks:(a)Hd(minH);(b)DD entropy;(c)Wu entropy;(d)SD entropy;(e)NB entropy;(f)EB entropy.

3.4 美国西部电网

为了进一步阐述K-阶结构熵评估网络异构性的能力,本文以某一公用数据集为例进行说明.该数据集为美国西部电网[18],描述了美国西部高压输电网的拓扑结构,共有4941个节点,代表发电厂、变电站以及中间电气连接点等场所;网络共有6594条边,代表输电线和变压器支路.该网络规定各节点无差别,且忽略输电线的物理构造及电气参数差异,即认为各边无差异,且无向无权.

Watts和Strogatz首次揭示了美国西部电网的小世界性,认为该网络同时具有近似于同规模随机网络的较短的特征路径长度,以及远大于随机网络的平均聚类系数[18].表1列出了美国西部电网与同规模随机网络的平均聚类系数、特征路径长度等参数.

表1 美国西部电网及同规模随机网络的网络参数Table 1.Network features of the Western Power Grid of the United States and random networks.

由表1可知,美国西部电网的特征路径长度仅为随机网络的2.33倍,而平均聚类系数是随机网络的510倍,以文献[18]的观点可认为美国西部电网是具有小世界性的.下面将基于K-阶结构熵对美国西部电网进行考察.

图9仿真了美国西部电网以及同规模最近邻耦合网络、WS小世界网络、随机网络和BA无标度网络在不同影响力尺度K下的结构熵.由图9可见,美国西部电网的结构熵随K先减少后增加,其minH约为11.95,与p=0.01下的WS小世界网络最为接近(minH=11.997),远大于BA无标度网络(minH=11.544),且小于随机网络(minH=12.187).因此,从最强异构性minH的角度出发,可认为美国西部电网的异构性与小世界网络相似,与前文平均聚类系数、特征路径长度等特性的分析结果以及相关文献[18,25-27]的研究均保持一致.

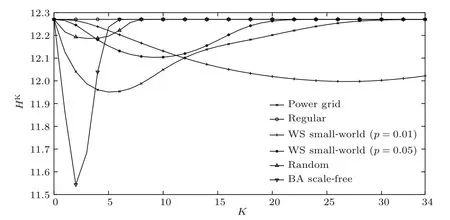
图9 美国西部电网、最近邻耦合网络、WS小世界网络、随机网络以及BA无标度网络在不同影响力尺度K下的结构熵Fig.9.K-order structure entropy at different in fluence scale K of the Western Power Grid of the United States,nearest-neighbor coupled networks,WS small-world networks,random networks and BA scale-free networks.

前文指出,网络的异构性还应从结构熵随K值的变化规律等方面予以考察.然而,美国西部电网的结构熵HK随K的变化曲线却与WS小世界网络、BA无标度网络等模型存在较大的差异.其中,该电网minH所对应的K值为5,远小于p=0.01下的WS小世界网络(K=27),与随机网络(K=3)和BA无标度网络(K=2)更为接近.事实上,Barabási和Albert等以美国西部电网为研究对象时指出,该电力网络的度分布符合γ≈4的幂率形式,具有一定的无标度性[21],而WS小世界模型的度分布却为泊松形式.此外,BA无标度模型的度分布虽为幂率形式,但其幂指数γ=3,与美国西部电网比较也存在差异;且BA无标度模型的聚类系数较小,无法体现美国西部电网的小世界性.

可见,若从minH的角度出发,可认为美国西部电网的异构性与小世界网络相似,但若从K-阶结构熵随K值的变化规律的角度出发,美国西部电网的异构性又与随机网络、WS小世界网络、BA无标度网络均不相同.目前,本文未能定量地给出HK随K值的变化规律与网络特性之间的关系,不能确定美国西部电网的全部性质,且美国西部电网也十分复杂,并不完全符合WS小世界、BA无标度等传统的理论模型.因此,深入探寻结构熵随K值的变化规律与网络特性之间的关系、探寻幂指数与minH等指标的关系、提出更符合诸如美国西部电网等实际网络的模型,均为未来的工作提出了新的要求.

值得注意的是,本文是通过定义K-阶邻居数来计算K-阶结构熵的,K-阶邻居数表征了某节点在K步内可达的节点总数,在一定程度上反映了节点的重要性,而节点重要性排序是研究网络传播效率等网络功能的重要前提.显然,节点重要性的排序将依K值的选择而有所不同.依前文所述,当网络具有最强的异构性时,各节点重要性分化达到最大限度.因此,选择minH所对应的K值作为节点重要性排序的参数是最为合理的.此外,K-阶邻居数还可以作为社区结构划分以及研究网络传播效率的依据.以社区结构划分为例,由于社区内部节点间的连接较为密集,而社区之间的连接则相对稀疏,因此社区中心节点的K-阶邻居数往往较多,而社区边界节点的K-阶邻居数则相对较少.由此,通过寻找被边缘节点所分割的中心节点,便可实现网络社区结构的自然划分.这里仍可将minH所对应的K值作为社区结构划分的参数选择.而基于K-阶邻居数的节点重要性排序、社区结构划分及网络传播等其他研究的具体过程本文不再展开叙述.

4 结 论

本文依据网络节点在不同影响力尺度下的K-阶邻居数提出了一种K-阶结构熵模型来评价网络的异构性.K-阶结构熵不是依据单一指标对网络进行分析,而是基于不同的影响力尺度K对网络的异构性进行多角度的讨论.研究发现,K-阶结构熵随K的变化规律、最大影响力尺度d下的异构性Hd以及网络能够达到的最强异构性minH均可以从不同的角度反映网络的异构性.通过对规则网络、随机网络、WS小世界网络、BA无标度网络和星型网络的理论研究和仿真分析发现,K-阶结构熵模型能够克服DD熵、Wu熵、SD熵、EB熵无法充分依据小世界属性来反映网络异构性的缺陷,并弥补了DD熵以及NB熵对星型网络解释的不足,且K-阶结构熵对在规则结构外新增孤立节点的网络异构性的解释也优于其他结构熵.此外,本文还基于K-阶结构熵对美国西部电网进行了讨论.由于本文的主要工作集中于提出新的网络结构熵模型以及利用经典的网络结构进行实验分析,对于网络结构熵的定量计算、结构熵随K值的变化规律与网络结构特性之间的关系、基于K-阶结构熵的节点重要性排序、社区结构划分等其他应用将会是后续研究的重点.值得注意的是,本研究仅探索了在规则结构外新添孤立节点的特殊情况,对其他拓扑结构添加孤立节点后,结构熵随K的变化规律、Hd与minH之间的关系等问题也仍需进一步探索.