探究高考题中离心率背后的“秘密”
■河南省项城市第一高级中学 韩维峥
离心率是圆锥曲线的重要几何性质,是描述圆锥曲线形状的重要参数。圆锥曲线离心率的确定与应用是高考的高频考点。“求圆锥曲线的离心率的值或取值范围”是常见题型,认真研究可以发现,单独考查离心率求法的题目很少,多数情况下是以离心率为背景,考查平面几何、平面向量、直线方程、解三角形等知识的综合运用,体现了知识的综合性和交汇性,这是高考命题的热点和方向。如何应对这种复杂的变化呢?笔者觉得,还是“万变不离其宗”,这里的“宗”就是建立恰当的等量关系或不等关系,以得到含有离心率e的等式或不等式,使问题得到解决。
一、方法突破
1.定义法。
例1已知椭圆的一个焦点为(2,0),则C的离心率为( )。

分析:根据题中所给的条件“一个焦点为(2,0)”,结合c2=a2-b2,求得a,c的值,再代入求得离心率。
解:由已知得c=2,因为b2=4,所以a2=b2+c2=8,即,所以椭圆C的离心率为故选C。
点评:本题考查椭圆离心率的求值,在求解的过程中,一定要注意条件“一个焦点为(2,0)”的隐含之意是“焦点在x轴上”,牢记离心率公式,结合椭圆中a,b,c的关系求得结果,此题较易。
2.向量法。
例2设F1,F2是双曲线(a>0,b>0)的左、右焦点,O是坐标原点。过F2作C的一条渐近线的垂线,垂足为P。若,则C的离心率为( )。
分析:由双曲线性质得到|P F2|=b,|P O|=a,由向量运算可知两边平方相加建立a,c的关系得离心率。
解:由题意可知|P F2|=b,|O F2|=c,所
点评:本题以考查双曲线的离心率为背景,综合运用平面向量的知识和双曲线的性质c2=a2+b2,使问题得以解决,属于中档题。
3.几何法。
例3已知F1,F2是椭圆1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,△P FF12为等腰三角形,∠F1F2P=120°,则C的离心率为( )。

分析:过P作x轴的垂线,构造直角三角形,在直角三角形中,利用三角函数建立a,c的关系,求得离心率。
解:如图1,过P作x轴的垂线,垂足为M。

点评:本题以考查椭圆的离心率的求值为背景,综合运用平面几何知识、直线斜率的几何意义、椭圆的几何性质,建立关于a,c的等量关系,使问题得以解决,属于中档题。
4.代数法。
分析:由直线与圆的位置关系知,圆心到直线的距离等于半径,从而得到a,b的关系,消去b可得离心率。
解:以线段A1A2为直径的圆是x2+y2=a2。因为直线b x-a y+2a b=0与圆相切,所以圆心到直线的距离a,整理得a2=3b2,所以a2=3(a2-c2)即选A。
点评:本题以考查椭圆的离心率为背景综合运用直线与圆相切的性质、点到直线的距离公式、椭圆的性质c2=a2-b2,建立关于a,c的等量关系,使问题得以解决,属于中档题。
二、一题多解
例5已知O为坐标原点,F是椭圆)的左焦点,A,B分别为C的左、右顶点。P为C上一点,且P F⊥x轴。过点A的直线l与线段P F交于点M,与y轴交于点E。若直线BM经过O E的中点,则C的离心率为( )。

分析:本题以椭圆内点线的交错关系为条件,而目标是求椭圆的离心率,所以思考方向自然是要得到a,b,c满足的等量关系,那么方向不外乎两个:利用坐标关系或几何关系,抓住条件“直线BM经过O E的中点”作为突破口,适当转化,获得所需等式。
解法一:如图2所示,设直线BM与y轴的交点为N,点N的坐标设为(0,m),根据题意,N是O E的中点,则E(0,2m),从而直线A E的方程为,直线BN的方程为又因为直线A E与直线BN交于点M,且P F⊥x轴,可设消去m,n,得,所以椭圆C的离心率为
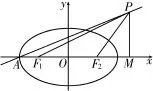
图1
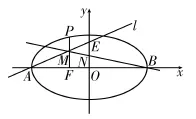
图2
解法二:同解法一得直线A E的方程为由题意可知N(0,m),B(a,0)三点共线,则
解法三:在△A O E中,MF∥O E,所以在△B FM中,ON∥MF,所以,即a+c=2(a-c),解得
解法四:由题意设直线l的方程为y=k(x+a),分别令x=-c与x=0,得|FM|=|k|(a-c),|O E|=k a,设O E的中点为N,由△O BN∽△F BM,得即,整理得,所以椭圆C的离心率为
点评:本题以考查椭圆的离心率为背景,综合运用平面几何知识、三点共线、直线方程和椭圆的性质进行多角度突破,体现了高考的立意和命题思想。离心率问题主要有三种常用思路:(1)直接求得a,c的值,进而求得e的值;(2)建立a,b,c的齐次等式,求得b
a或转化为关于e的等式求解;(3)通过特殊值或特殊位置,求出e。本题给出了四种方法,其中解法一、解法二运用代数法建立a,c的关系,运算量比较大,加大了算错的概率,而解法三、解法四运用了几何法,利用数形结合建立a,c的关系,减少了运算量,所以在解决椭圆的离心率求值问题时,要充分考虑几何性质,优化解题思路。
三、应用体验
例6(2018年全国卷Ⅱ)已知F1,F2是椭圆C的两个焦点,P是C上的一点,若P F1⊥P F2,且∠P F2F1=60°,则C的离心率为( )。
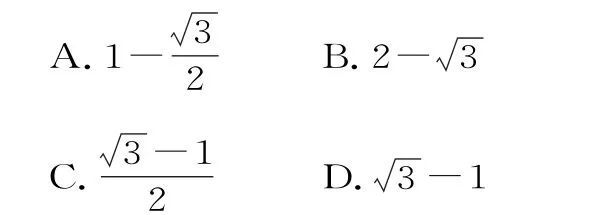
分析:设|P F2|=m,则根据平面几何知识可求|F1F2|,|P F1|,再结合椭圆定义可求离心率。
解:在 △F1P F2中,∠F1P F2=90°,∠P F2F1=60°,设|P F2|=m,则 2c=|F1F2|=2m,|P F1|=3m。
由椭圆定义可知2a=|P F1|+|P F2|=则离心率
点评:椭圆定义的应用主要有两个方面:一是判断平面内动点与两定点的轨迹是否为椭圆;二是利用定义求焦点三角形的周长、面积,以及椭圆的弦长和离心率等问题。“焦点三角形”是椭圆问题中的常考知识点,在解决这类问题时经常会用到正弦定理、余弦定理及椭圆的定义。
例7(2017年全国卷Ⅱ(理)若双曲线的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2,则C的离心率为( )。

分析:利用弦长和点到直线的距离公式可以得到b,c满足的方程,再消去b得a,c满足的方程,从而求得离心率。
解:已知双曲线的渐近线方程为b x±a y=0,圆心(2,0)到渐近线的距离为,则点(2,0)到直线b x-a y=0的距离为,整理可得c2=4a2,所以离心率故选A。
点评:本题以考查双曲线的离心率为背景,综合运用圆的弦长公式及点到直线的距离公式,所以本题要充分利用好圆的半径、弦长的一半、圆心到弦的距离,三者之间满足勾股定理,可得b,c满足的齐次式,再结合b2=c2-a2,消去b得a,c满足的齐次式,然后等式两边分别除以a或a2转化为关于e的方程,解方程即可得e。
例8(2017年全国卷Ⅱ(文)若a>1,则双曲线的离心率的取值范围是( )。
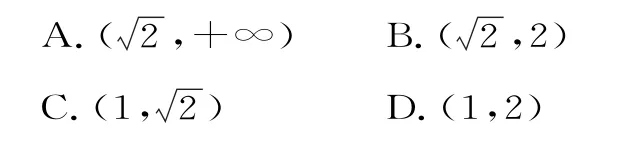
分析:利用离心率的计算公式得到e的表达式,再利用函数思想求得e的取值范围。
解:因为c2=a2+1,所以
点评:本题考查的是双曲线离心率的取值范围,解题关键是建立e,a的关系,即用a去表示e,再运用函数值域的求法求得结果难度一般。
高考题千变万化、常出常新,命题人更是人才济济、别出心裁,对我们学生来说,能够立足根本、以不变应万变才是正确的备考之路。

