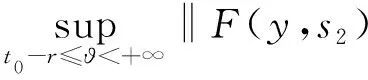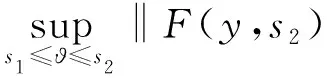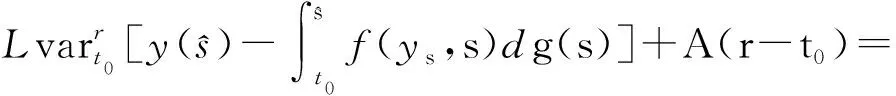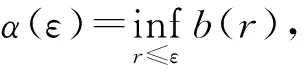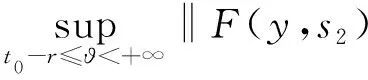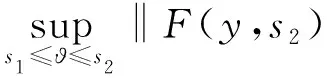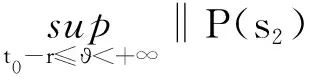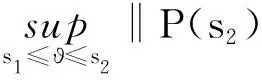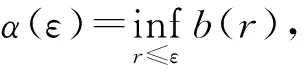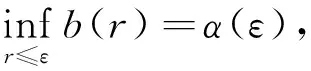滞后型测度泛函微分方程的变差稳定性

李宝麟, 刘静芳

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

当常微分方程

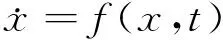
所描述的系统受到扰动时,对受扰动系统导出的常微分方程的形式为

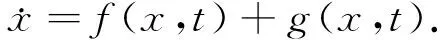
如果扰动项是连续可积的,那么扰动后的系统仍然为常微分方程系统,它的解为连续的.若扰动为脉冲型的,则扰动后系统的状态就不随时间连续变化,而是呈现一种瞬时性态.对这种数学模型的研究导出另一类方程即测度微分方程,其一般形式为

Dx=f(x,t)+g(x,t)Du.

(1)

Dy=f(yt,t)Dg

(2)

和它所描述的系统受到扰动后的滞后型测度泛函微分方程

Dy=f(yt,t)Dg+p(t)Du,

(3)

并定义了滞后型测度泛函微分方程的积分稳定性与广义常微分方程的正则稳定性,证明了滞后型测度泛函微分方程的积分稳定性等价于广义常微分方程的正则稳定性.在(2)和(3)式中,Dy、Dg、Du分别是y、g、u的分布导数,f:S×[t0,+∞)→Rn,g,u:[t0,+∞)→R,y:[t0-r,+∞)→Rn,yt(θ)=y(t+θ),θ∈[-r,0],r>0,p:[t0,+∞)→Rn,且

S={yt:y∈O,t∈[t0,+∞)}⊂G*([-r,0],Rn),

O⊂G*([t0-r,+∞),Rn), r>0.

上述的O为开集,G*([t0-r,+∞),Rn)表示[t0-r,+∞)到Rn所有的有界正则函数全体.由文献[9]知,方程(2)等价于积分方程

t∈[t0,+∞);

(4)

方程(3)等价于积分方程

(5)

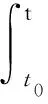
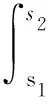
(H2) 对任意的y∈O,s1,s2∈[t0,+∞),存在常数M>0,使得

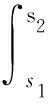
(H3) 对任意的y,z∈O,s1,s2∈[t0,+∞),存在常数N>0,使得

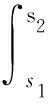
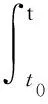
(H5) 对任意的t∈[t0,+∞),s1,s2∈[t0,+∞),存在常数K>0,使得

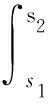
受到以上工作的启示,本文利用广义常微分方程的稳定性理论研究滞后型测度泛函微分方程(2)和(3)的变差稳定性和变差渐近稳定性.

1 预备知识

下面主要介绍广义常微分方程与滞后型测度泛函微分方程的相关概念及其引理.

定义1.1[3]给定一个函数δ(t):[a,b]→(0,+∞),对区间[a,b]上的一个分划

D:a=α0<α1<<αk=b,

如果有

[αi-1,αi]⊂[τ-α(τi),τ+α(τi)], i=1,2,,k,

称分划D为[a,b]上的δ-精细分划.

定义1.2[3]设函数U:[a,b]×[a,b]→Rn,如果存在I∈Rn,使得对任意的ε>0,存在正值函数δ:[a,b]→(0,+∞),且对[a,b]上的任何的δ-精细分划

D={(τj,[αi-1,αi]),j=1,2,,k},

其中

τj∈[αi-1,αi]⊂[τj-δ(τj),τj+δ(τj)],

有

称函数U:[a,b]×[a,b]→Rn在[a,b]上为Henstock-Kurzweil可积的.此时记作

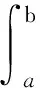
设G:Ω→Rn,Ω=O×[t0,+∞).

定义1.3[3]设函数G:Ω→Rn,如果对所有的t∈[α,β],(x(t),t)∈Ω,任意的s1,s2∈[α,β],有等式

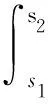
成立,则称x:[α,β]→Rn是广义常微分方程

在区间[α,β]⊂[t0,+∞)上的解.

定义1.4[9]设不减函数h:[t0,+∞)→R,如果函数G:Ω→Rn满足:对任意的(x,s1),(x,s2)∈Ω,有

‖G(x,s2)-G(x,s1)‖∞≤|h(s2)-h(s1)|;

对任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω,有

‖G(x,s2)-G(x,s1)-G(y,s2)+G(y,s1)‖∞≤

‖y-z‖∞|h(s2)-h(s1)|,

则函数G属于函数族F(Ω,h).

引理1.1[9]设f:S×[t0,+∞)→Rn满足(H1)～(H3),函数g:[t0,+∞)→R为不减的,对于y∈O,t∈[t0,+∞),定义如下函数

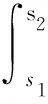
F(y,t)(ϑ)=

(6)

则F∈F(Ω,h),其中

F:O×[t0,+∞)→G*([t0-r,+∞),Rn).

引理1.2[9]考虑广义常微分方程

(7)

其中F由(6)式给定,函数h:[t0,+∞)→R定义如下

h(t)=(M+N)[g(t)-g(t0)],

t∈[t0,+∞),

(8)

则由h定义可知h为[t0,+∞)上不减的左连续函数.

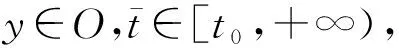
引理1.3[9]设O是G*([t0-r,+∞),Rn)的开子集,且t∈[t0,+∞)时,具有延拓性质,S={yt:y∈O,t∈[t0,+∞)},φ∈S,g:[t0,+∞)→R是不减函数,f:S×[t0,+∞)→Rn满足条件(H1)～(H3).

(i) 假设对于任意的y∈O,t∈[t0,+∞).如果y:[t0-r,+∞)→O是滞后型测度泛函微分方程

的解.

对任意的t∈[t0-r,+∞),有

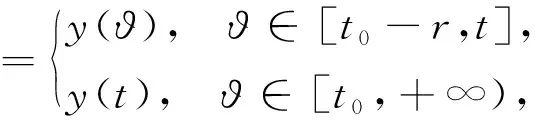
则函数x:[t0,+∞)→O是广义常微分方程

在初值条件

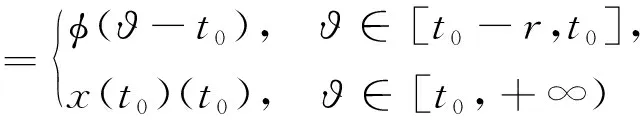
下的解,其中F由(6)式给定.

(ii) 相反地,F由(6)式给定,如果x:[t0,+∞)→O是广义常微分方程

的解,且满足初值条件

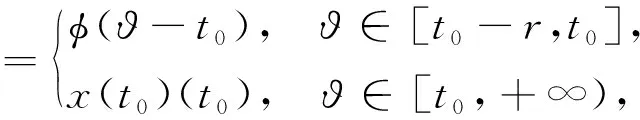
则函数y:[t0-r,+∞)→O是滞后型测度泛函微分方程

在初值条件

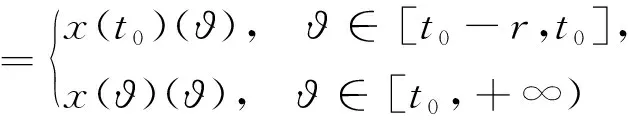
下的解.

引理1.4[9]设f:S×[t0,+∞)→Rn满足(H1)～(H3),且p:[t0,+∞)→Rn满足(H4)和(H5),函数g,u:[t0,+∞)→R为不减的,对于y∈O,t∈[t0,+∞),定义如下函数

F(y,t)(ϑ)=

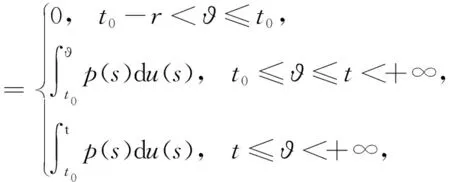
则有

G(y,t)=F(y,t)+P(t),

(9)

且G∈F(Ω,h),其中

G:O×[t0,+∞)→G*([t0-r,+∞),Rn).

引理1.5[9]考虑广义常微分方程

(10)

其中G由(9)式给定,函数h1,h2:[t0,+∞)→R,有如下定义

h1(t)=(M+N)[g(t)-g(t0)],

h2(t)=K[u(t)-u(t0)],

t∈[t0,+∞).

(11)

定义h:[t0,+∞)→R如下

h(t)=h1(t)+h2(t),t∈[t0,+∞),

则由定义可知h1、h2、h为[t0,+∞)上不减的左连续函数.

引理1.6[9]设O是G*([t0-r,+∞),Rn)的开子集,且t≥t0时,具有延拓性质,S={yt:y∈O,t∈[t0,+∞)},φ∈S,u,g:[t0,+∞)→R是不减函数,f:S×[t0,+∞)→Rn满足条件(H1)～(H3),且p:[t0,+∞)→Rn满足(H4)和(H5).

(i) 假设对于任意的y∈O,t∈[t0,+∞),如果y:[t0-r,+∞)→O是滞后型测度泛函微分方程

的解.

对任意的t∈[t0-r,+∞)有

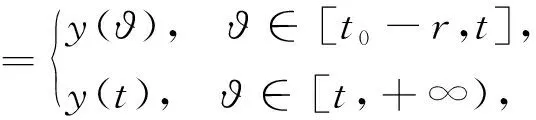
则函数x:[t0,+∞)→O是广义常微分方程

在初值条件

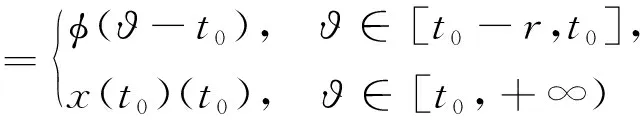
下的解,G由(9)式给定.

(ii)相反地,G由(9)式给定,如果x:[t0,+∞)→O是广义常微分方程

的解,且满足初值条件

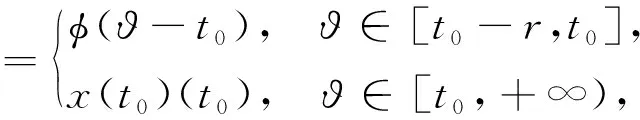
则函数y:[t0-r,+∞)→O是滞后型测度泛函微分方程

在初值条件

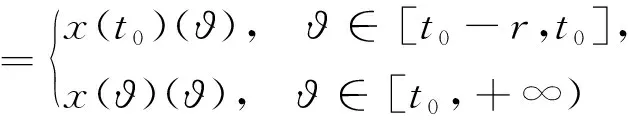
下的解.

引理1.7[3]设V:Rn×[0,+∞)→R,对于任意的y∈Rn,函数V(y,·):[0,+∞)→R在区间(0,+∞)上是左连续的,假设以下条件成立:

(i) 对于任意的(x,t),(y,t)∈Rn×[0,+∞),常数L>0,有

|V(x,t)-V(y,t)|≤L‖x-y‖∞;

(ii) 存在一个实函数Φ:Rn→R,使得对于滞后型测度泛函微分方程(2)在区间[t0,+∞)⊂[0,+∞)上的每一个解y:[t0,+∞)→Rn,对t∈[t0,+∞)有

Φ(y(t));

(12)

如果

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,则不等式

V(y(t1),t1)≤V(y(t0),t0)+

(13)

成立,其中

F由(6)式给定.

引理1.8[3]设V:Rn×[0,+∞)→R,对于任意的y∈Rn,函数V(y,·):[0,+∞)→R在区间(0,+∞)上是左连续的,假设以下条件成立：

(i) 对于任意的(x,t),(y,t)∈Rn×[0,+∞),常数L>0,有

|V(x,t)-V(y,t)|≤L‖x-y‖∞;

(ii) 存在一个实函数Φ:Rn→R,使得对于滞后型测度泛函微分方程(3)在区间[t0,+∞)⊂[0,+∞)上的每一个解y:(t0,+∞)→Rn,对t∈(t0,+∞)有

Φ(y(t));

(14)

如果

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,则不等式

V(y(t1),t1)≤V(y(t0),t0)+

(15)

成立,其中

G由(9)式给定.

2 主要结果

下面主要讨论滞后型测度泛函微分方程(2)与受到扰动后的滞后型测度泛函微分方程(3)的变差稳定性与变差渐近稳定性,利用广义常微分方程的稳定性理论给出滞后型测度泛函微分方程的变差稳定性定理及其证明.

定义2.1如果对于任意的ε>0,存在δ=δ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,当‖y(t0)‖∞<δ和

(16)

其中F由(6)式给定.对于任意的t∈[t0,t1],有‖y(t)‖∞<ε,则称滞后型测度泛函微分方程(2)的解y≡0是变差稳定的.

定义2.2如果存在δ0>0,对于任意的ε>0,有T=T(ε)≥0和γ=γ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,当‖y(t0)‖∞<δ0和

(17)

其中F由(6)式给定.对于任意的t∈[t0,t1]∩[t0+T(ε),+∞),且t0≥0时,有‖y(t)‖∞<ε,则称滞后型测度泛函微分方程(2)的解y≡0是变差吸引的.

定义2.3如果滞后型测度泛函微分方程(2)的解既是变差稳定的,又是变差吸引的,则称滞后型测度泛函微分方程(2)的解是y≡0是变差渐近稳定的.

定义2.4如果对于任意的ε>0,存在δ=δ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,当‖y(t0)‖∞<δ和

(18)

其中G由(9)式给定.对于任意的t∈[t0,t1],有‖y(t)‖∞<ε,则称滞后型测度泛函微分方程(3)的解y≡0是变差稳定的.

定义2.5如果存在δ0>0,对于任意的ε>0,有T=T(ε)≥0和γ=γ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,当‖y(t0)‖∞<δ0和

(19)

其中G由(9)式给定.对于任意的t∈[t0,t1]∩[t0+T(ε),+∞),且t0≥0时,有‖y(t)‖∞<ε,则称滞后型测度泛函微分方程(3)的解y≡0是变差吸引的.

定义2.6如果滞后型测度泛函微分方程(3)的解既是变差稳定的,又是变差吸引的,则称滞后型测度泛函微分方程(3)的解是y≡0是变差渐近稳定的.

定理2.1设V:O×[0,+∞)→R,使得对于任意的y∈O⊂G*([t0-r,+∞),Rn),r>0,函数V(y,·):[0,+∞)→R在区间(0,+∞)上是左连续的.假设V(y,·)是正定的,即存在一个连续递增实函数b:[0,+∞)→R,使得b(ρ)=0当且仅当ρ=0,对所有的(y,t)∈O×[0,+∞),任意的x∈O,常数L>0,有:

V(y,t)≥b(‖y‖∞),

(20)

V(0,t)=0,

(21)

和

|V(x,t)-V(y,t)|≤L‖x-y‖∞.

(22)

如果函数V(y(t),t)对滞后型测度泛函微分方程(2)的任何一个解y(t)是不增函数,则方程(2)的平凡解y≡0是变差稳定的.

证明由引理1.1,验证F∈F(Ω,h),Ω=O×[t0,+∞).由假设存在常数M、N,对于任意的y,z∈O,条件(H1)暗示了在F的定义下积分存在,给定y∈O,且0≤t0

F(y,s2)(ϑ)-F(y,s1)(ϑ)=

则由条件(H2)有

‖F(y,s2)(ϑ)-F(y,s1)(ϑ)‖∞=

M[g(s2)-g(s1)]≤h(s2)-h(s1),

由条件(H3)有

‖F(y,s2)(ϑ)-F(y,s1)(ϑ)-

F(z,s2)(ϑ)+F(z,s1)(ϑ)‖∞=

‖y-z‖∞[h(s2)-h(s1)].

由引理1.3知,滞后型测度泛函微分方程(2)与广义常微分方程(7)在一定条件下等价,故它们的解均为有界变差函数且可以相互表示.以下证明滞后型测度泛函微分方程(2)的平凡解y≡0为变差稳定的.由假设V(y(t),t)对方程(2)的任何一解y:[t0,+∞)→Rn是不增函数,对任意的t∈[t0,+∞)有

以下证明在这种假设下满足定义2.1的条件.

给定ε>0,令

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续.由于V满足引理1.7的(12)式,其中Φ≡0.由(13)、(21)和(22)式,对于任意的r∈[t0,t1]可得

因为

|V(y(t0),t0)-V(0,t0)|≤L‖y(t0)‖∞,

且Φ≡0,所以

‖y(t0)‖∞<δ(ε).

由(16)式得

由(23)式有

V(y(r),r)≤L‖y(t0)‖∞+Lδ(ε)≤

Lδ(ε)+Lδ(ε),

所以当r∈[t0,t1]时,有以下不等式成立

V(y(r),r)≤2Lδ(ε).

(24)

如果存在ξ∈[t0,t1],使得‖y(ξ)‖∞≥ε,根据(20)式有

这与(24)式矛盾,故对于所有的t∈[t0,t1]有‖y(t)‖∞<ε,满足定义2.1,即滞后型测度泛函微分方程(2)的平凡解y≡0是变差稳定的.

定理2.2设V:O×[0,+∞)→R满足定理2.1中的条件,如果对于滞后型测度泛函微分方程(2)的任何一个解y:[t0,t1]→O,当t∈[t0,t1]时有

-Φ(y(t))

(25)

成立,其中Φ:Rn→R为连续函数且Φ(0)=0.当y≠0时,Φ(y)>0,则滞后型测度泛函微分方程(2)的平凡解y≡0为变差渐近稳定的.

证明由(25)式知,V(y(t),t)对滞后型测度泛函微分方程(2)的任何一个解y:[t0,t1]→Rn是不增函数.由定理2.1可知,滞后型测度泛函微分方程(2)的平凡解y≡0是变差稳定的,由定义2.3可知以下只需证明滞后型测度泛函微分方程(2)的平凡解y≡0是变差吸引的.

由定理2.1,滞后型测度泛函微分方程(2)的平凡解是变差稳定的,存在一个δ0>0,对任意的

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,使得‖y(t0)‖∞<δ0,且有

则对任意的t∈[t0,t1],有‖y(t)‖∞<δ0.对任意的ε>0,由滞后型测度泛函微分方程(2)的平凡解y≡0是变差稳定的可知,存在δ(ε)>0,使得对于每一个

y:[t2,t3]→Rn, 0≤t2

是区间[t2,t3]上的有界变差函数,并且在(t2,t3]上左连续,使得

‖y(t0)‖∞<δ(ε)

(26)

和

则对于t∈[t2,t3]有

‖y(t)‖∞<ε.

(28)

定义

γ(ε)=min(δ0,δ(ε)),δ0>0,

其中

A=sup{-Φ(y);γ(ε)≤‖y‖∞<ε}=

-inf{Φ(y);γ(ε)≤‖y‖∞<ε}<0,

且假设

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,使得‖y(t0)‖∞<δ0,且有

假设T(ε)

下面证明存在一个t*∈[t0,t0+T(ε)],使得有‖y(t*)‖∞<γ(ε).

运用反证法.假设上述结论不成立,即对于任意的s∈[t0,t0+T(ε)]有

‖y(s)‖∞≥γ(ε).

由引理1.7得

因此

V(y(t0+T(ε)),t0+T(ε))≤

V(y(t0),t0)-Lδ0≤

L‖y(t0)‖∞-Lδ0

这与不等式

V(y(t0+T(ε),t0+T(ε))≥

b(‖y(t0+T(ε))‖∞)≥b(γ(ε))>0

矛盾,所以必然存在一个t*∈[t0,t0+T(ε)],使得

‖y(t*)‖∞<γ(ε).

对于t1=t*,t3=t1这种情况,考虑到γ(ε)的选取,由于(26)、(27)式成立,因而(28)式也满足.因此对于t>t0+T(ε),有‖y(t)‖∞<ε.由于t*∈[t0,t0+T(ε)],则滞后型测度泛函微分方程(2)的平凡解y≡0是变差吸引的.由定义2.3知滞后型测度泛函微分方程(2)的平凡解y≡0是变差渐近稳定的.

接下来讨论受到扰动后的滞后型测度泛函微分方程(3)的变差稳定性与变差渐近稳定性.

定理2.3设V:O×[0,+∞)→R,使得对于任意的y∈O⊂G*([t0-r,+∞),Rn),r>0,函数V(y,·):[0,+∞)→R在区间(0,+∞)上是左连续的,假设V(y,·)是正定的,即存在一个连续递增实函数b:[0,+∞)→R,使得b(ρ)=0当且仅当ρ=0,对所有的(y,t)∈O×[0,+∞),任意的x∈O,常数L>0有:

V(y,t)≥b(‖y‖∞),

(29)

V(0,t)=0,

(30)

和

|V(x,t)-V(y,t)|≤L‖x-y‖∞.

(31)

如果函数V(y(t),t)对滞后型测度泛函微分方程(3)的任何一个解y(t)是不增函数,则方程(3)的平凡解y≡0是变差稳定的.

证明由引理1.4,验证G∈F(Ω,h),Ω=O×[t0,+∞).根据假设存在常数M、N、K,对于任意的y,z∈O.条件(H1)和(H4)暗示了在G的定义下积分存在,给定y∈O,若0≤t0

F(y,s2)(ϑ)-F(y,s1)(ϑ)=

P(s2)(ϑ)-P(s1)(ϑ)=

则由条件(H2)和(H5)有

‖F(y,s2)(ϑ)-F(y,s1)(ϑ)‖∞=

h1(s2)-h1(s1),

‖P(s2)(ϑ)-P(s1)(ϑ)‖∞=

h2(s2)-h2(s1),

即

‖G(y,s2)(ϑ)-G(y,s1)(ϑ)‖∞≤h1(s2)-

h1(s1)+h2(s2)-h2(s1)≤h(s2)-h(s1).

由条件(H3)有

‖G(y,s2)(ϑ)-G(y,s1)(ϑ)-

G(z,s2)(ϑ)+G(z,s1)(ϑ)‖∞=

‖y-z‖∞[h(s2)-h(s1)].

存在.因此,G∈F(Ω,h),其中h:[t0,+∞)→R为左连续不减函数,h1(t)、h2(t)由(11)式给出且

h(t)=h1(t)+h2(t).

由引理1.6知,滞后型测度泛函微分方程(3)与广义常微分方程(10)在一定条件下等价,故它们的解均为有界变差函数且可以相互表示,以下证明滞后型测度泛函微分方程(3)的平凡解y≡0为变差稳定的.由假设V(y(t),t)对方程(3)的任何一解y:[t0,+∞)→Rn是不增函数,对任意的t∈[t0,+∞)有

以下证明在这种假设下满足定义2.4的条件.

给定ε>0,令

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续.由于V满足引理1.8的(14)式,其中Φ≡0.由(15)、(30)和(31)式,对于任意的r∈[t0,t1],可得

(32)

因为

|V(y(t0),t0)-V(0,t0)|≤L‖y(t0)‖∞,

且Φ≡0,所以

‖y(t0)‖∞<δ(ε).

由(18)式得

由(32)式有

V(y(r),r)≤L‖y(t0)‖∞+

Lδ(ε)≤Lδ(ε)+Lδ(ε),

所以当r∈[t0,t1]时,有以下不等式成立

V(y(r),r)≤2Lδ(ε).

(33)

如果存在ξ∈[t0,t1],使得

‖y(ξ)‖∞≥ε,

根据(29)式有

V(y(ξ),ξ)≥b(‖y(ξ)‖∞)≥

这与(33)式矛盾,故对于所有的t∈[t0,t1]有

‖y(t)‖∞<ε

满足定义2.4,即滞后型测度泛函微分方程(3)的平凡解y≡0是变差稳定的.

定理2.4设V:O×[0,+∞)→R满足定理2.3中的条件,如果对于滞后型测度泛函微分方程(3)的任何一个解y:[t0,t1]→Rn,当t∈[t0,t1]时有

-Φ(y(t))

(34)

成立,其中Φ:Rn→R为连续函数且Φ(0)=0.当y≠0时,Φ(y)>0,则滞后型测度泛函微分方程(3)的平凡解y≡0为变差渐近稳定的.

证明由(34)式知,V(y(t),t)对滞后型测度泛函微分方程(3)的任何一个解y:[t0,t1]→Rn是不增函数.由定理2.3可知,滞后型测度泛函微分方程(3)的平凡解y≡0是变差稳定的,由定义2.6可知以下只需证明滞后型测度泛函微分方程(3)的平凡解y≡0是变差吸引的.

由定理2.3,滞后型测度泛函微分方程(3)的平凡解是变差稳定的,存在一个δ0>0,对任意的

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,使得‖y(t0)‖∞<δ0,且有

则对任意的t∈[t0,t1],有‖y(t)‖∞<δ0.对任意的ε>0,由滞后型测度泛函微分方程(3)的平凡解y≡0是变差稳定的可知,存在δ(ε)>0,使得对于每一个

y:[t2,t3]→Rn, 0≤t2

是区间[t2,t3]上的有界变差函数,并且在(t2,t3]上左连续,使得

‖y(t0)‖∞<δ(ε)

(35)

和

(36)

则对于t∈[t2,t3]有

‖y(t)‖∞<ε.

(37)

令

γ(ε)=min(δ0,δ(ε)),

其中

A=sup{-Φ(y);γ(ε)≤‖y‖∞<ε}=

-inf{Φ(y);γ(ε)≤‖y‖∞<ε}<0,

且假设

y:[t0,t1]→Rn, 0≤t0

是区间[t0,t1]上的有界变差函数,并且在(t0,t1]上左连续,使得‖y(t0)‖∞<δ0,且有

(38)

假设T(ε)

以下证明存在一个t*∈[t0,t0+T(ε)],使得‖y(t*)‖∞<γ(ε).

运用反证法.假设上述结论不成立,即对于任意的s∈[t0,t0+T(ε)],有‖y(s)‖∞≥γ(ε).由引理1.7得

因此

V(y(t0+T(ε)),t0+T(ε))≤

V(y(t0),t0)-Lδ0≤

L‖y(t0)‖∞-Lδ0

这与不等式

V(y(t0+T(ε),t0+T(ε))≥

b(‖y(t0+T(ε))‖∞)≥b(γ(ε))>0

矛盾,所以必然存在一个t*∈[t0,t0+T(ε)],使得

‖y(t*)‖∞<γ(ε).

对于t1=t*,t3=t1这种情况,考虑到γ(ε)的选取,由于(35)和(36)式成立,因而(37)式也满足.对于t>t0+T(ε),有‖y(t)‖∞<ε.由于t*∈[t0,t0+T(ε)],则滞后型测度泛函微分方程(3)的平凡解y≡0是变差吸引的.由定义2.6知滞后型测度泛函微分方程(3)的平凡解y≡0是变差渐近稳定的.