广义非线性模型的Bayes估计*
刘洋洋,陈 萍
(南京理工大学 理学院 南京 210094)
0 引 言
近年来,Bayes统计推断取得了重大的发展,并且随着Bayes方法的发展,该方法的优点也得到了充分的体现.通常Bayes方法的优点可以概括为4点:它考虑了模型参数的先验信息,并且参数的先验信息用得越好,参数估计的精度就越高;该方法通常能够较好地应用于小样本情形;能用抽样的方法估计参数的后验分布;能用抽样的方法估计后验分布的数字特征,如后验期望、后验方差、后验众数和后验分位数等.在Bayes统计分析的问题中,蒙特卡洛抽样(MCMC)方法的应用比较广泛,特别是MCMC方法中的M-H抽样算法和Gibbs抽样算法在参数估计的领域里运用得也比较多.本文利用这两种算法针对广义非线性模型的参数估计问题,提出从参数的条件后验分布中抽取观测值来估计参数值Bayes的方法,并用实例分析验证了该方法的有效性和可行性.
1 广义非线性模型
给定数据集(xi,yi),i=1,2,…,n,设各yi之间相互独立,E(yi)=μi,则广义非线性模型可表示为
g(μi)=f(xi,β)
yi~ED(μi,σ2),i=1,2,…,n
(1)
其中g(·)是严增可微函数,称为联系函数;ED(μi,σ2)表示指数族分布(陈希孺,1981;韦博成,2006),yi=μ(xi,β)+εi,i=1,2,…,n,其中εi是均值为0的随机误差,即E(εi)=0.
yi的密度函数可表示为
p(yi;θi,φ)=
(2)
其中,θi称为自然参数,σ2=φ-1称为离差参数,并记μ=(μ1,μ2,…,μn)T,θ=(θ1,θ2,…,θn)T,根据指数族分布的性质,有:
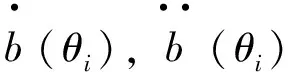
在广义非线性模型中有广泛应用的偏差度概念,它相当于普通回归模型中的残差平方和,与尺度参数的估计有密切关系.对于广义非线性模型式(1),其偏差度函数定义为
d(yi,μi)=-2[yiθi-b(θi)-c(yi)]
因此式(1)可表示为β和σ2的函数,即
p(yi;μi(β),σ2)=
(3)
由于各yi之间相互独立,因此可得广义非线性模型的概率密度函数为
2 模型的Bayes分析
2.1 分析方法
由Bayes公式可得模型参数的后验密度为
p(β,σ2∣y,x)=
p(y∣β,σ2,x)p(β,σ2)=
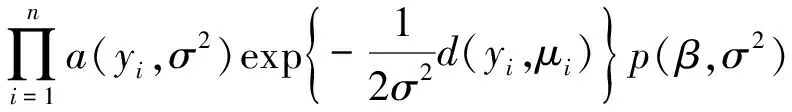
(4)
由式(4)可知,要得到参数的后验分布,要先指定参数的先验分布.因为参数β是模型的回归系数,σ2是随机误差分布的散度参数,所以通常假定p(β,σ2)=p(β)p(σ2),假设p(β)和p(σ2)分别取为多元正态分布和逆Gamma分布,即假定参数β和σ2=φ-1的先验分布为β~N[υ0,∑0],φ~Gamma(α0,ρ0),故β和φ的联合后验分布可表示为
φα0-1exp{-φρ0}
因此,可得参数β的条件分布为
(β-υ0)T∑0-1(β-υ0)]}
(5)
参数φ的条件分布为
p(φ∣β,y,x)∝
(6)
如果a(yi,φ-1)为与φ无关的常数,则
如果a(yi,φ-1)∝φτexp {φ-k},则
p(φ∣β,y,x)~Gamma(α0+nτ,nk+
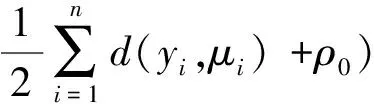
(7)
由式(5)和式(6)可以看出,条件分布p(β∣φ,y,x)和p(φ∣β,y,x)一般都是一些非标准分布而且很复杂,不能直接从这些分布中抽取Bayes推断所需要的观测值,因此通常会采取MCMC方法中的Gibbs抽样算法或M-H算法或这两种算法相结合的混合算法来解决广义非线性模型中参数估计的问题.
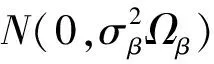
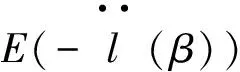
根据式(3),Y=(y1,y2,…,yn)T的对数似然函数可表示为
由此可得
采用M-H算法从式(5)中抽取观测样本,设参数β的第j步迭代值为β(j),则第(j+1)次迭代按如下步骤完成:
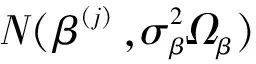

其中
采用M-H算法从式(6)中抽取观测样本,设φ的第j步迭代值为φ(j),则第(j+1)次迭代按如下步骤完成:
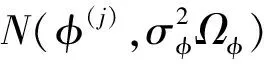
若经过计算发现有的参数条件分布可以用常见的标准分布表示出来,那么将选用Gibbs抽样算法对其进行参数估计.Gibbs抽样算法的一个优势就是所有抽样数据由一维分布产生,样本可以由标准统计分布生成;它不需要建议分布,每次接受新的样本值.由此可知,Bayes估计的Gibbs抽样算法步骤:
① 给定参数(β,φ)的初始值(β(0),φ(0)),并令j=0;
② 已知φ(j)从后验分布p(β∣φ(j),y,x)中抽取观测值β(j+1);
③ 已知β(j+1),从后验分布p(φ∣β(j+1),y,x)中抽取观测值φ(j+1);
④ 重复步骤②和步骤③得到β和φ的随机样本序列{β(j+1),φ(j+1):j=1,2,…,k}.
2.2 算法收敛性的诊断
无论使用哪一种抽样方法,都要确定所得到的马氏链的收敛性,即需要确定马氏链达到收敛状态时迭代的次数(达到收敛状态前的那一段链称为“预烧期”样本).通常没有一个全能的方法确定马氏链的收敛性,监视链的收敛性有许多方法,但是每种方法都是针对收敛性问题的不同方面提出的,因此,在绝大多数情况下,为了保证链的收敛性需应用几种不同的方法去诊断.常用的几种诊断方法为蒙特卡洛误差、样本路径图、遍历均值图、自相关函数图、Gelman-Rubin方法.本文采用的是利用样本路径图、遍历均值图来判断算法的收敛性.
样本路径图是指用马氏链迭代次数对生成的值作图,若所有的值都在一个区域里且没有明显的周期性和趋势性,那么可以假设收敛性已经达到.
遍历均值图是一种很有用的图方法,该方法是将马氏链的累积均值对迭代次数作图.这里累积均值是指此量直至当前迭代的平均值,如果累积均值在经过一些迭代后基本稳定,则表明算法已经达到收敛.
2.3 Bayes推断
本文采用的是M-H算法和Gibbs抽样算法的混合算法,假设在第l次迭代时已经收敛,则基于参数β和φ的观测值序列{β(j),φ(j):j=1,2,…,k},可得模型参数β和σ2=φ-1的Bayes估计.
(8)
(9)
令T=k-l,则由式(8)和式(9)给出的估计是相合估计,其相应后验协方差阵的相合估计为
因此,可以通过上述随机样本序列的样本协方差阵的对角元素得到其对应的标准误差.
3 实例分析
通过实例分析,利用MCMC方法中Gibbs抽样算法和M-H算法相结合的混合算法画出参数的样本路径图和均值遍历图,并求出广义非线性模型中参数的Bayes估计,然后和已知的极大似然估计值进行比较,从而验证该方法的有效性和可行性.
表1数据来自Whitmore(1986),在此数据中,xi表示经过市场调查得到的第i种产品的计划销售量,yi表示相应的实际销售量,Whitmore(1986)建议用以下逆高斯模型进行拟合:

(10)


表1 产品销售数据
3.1 模型分析
在逆高斯模型式(10)中,结合式(2),有
φ=k=σ2
c(yi)=(2(yi))-1
s(yi,φ)=-{logφ-log(2πyi3)}
d(yi,μi)=(yi-(μi))2/μi2yi
假设参数β,γ,k服从的先验分布分别为β~N(υ0,∑0),γ~N(γ0,τ0),k~Gamma(α0,ρ0).
根据式(5)可求得参数β和γ的条件分布,因为yi服从参数为μi和k=σ2的单形分布,故由式(7)可知,k的条件分布为Gamma分布,即
本例采用了混合抽样的算法,即对参数β和γ采用M-H算法,对参数k采用Gibbs抽样算法,然后用R软件进行编程,对模型进行分析和求解.
3.2 参数的MCMC诊断
以下图1和图2为参数β,γ和k的样本路径图和均值遍历图.

图1 参数β和γ的MCMC诊断图

图2 参数k的MCMC诊断图
由图1中(a)(b)和图2中的(e)可知参数β,γ和k的时间状态图显示链混合得较好,波动比较稳定,没有明显的周期性和趋势性,这说明链达到了平稳分布,由图1中(c)(d)和图2(f)可知参数β,γ和k的遍历均值图,从遍历均值图中可以看到去掉前8 000次迭代后所有的参数基本都趋于平稳,这也表明了链的收敛性较好.因此丢掉前8 000次迭代值,选用之后的32 000次迭代值的平均值作为参数的Bayes估计,从图2中可以看出链收敛后,参数均值的大致取值范围.
3.3 参数估计
表2中为3个参数的Bayes估计值、标准差以及和极大似然估计值相比时的偏差.从偏差的值可以判定参数的Bayes估计和极大似然估计几乎一致.

表2 产品销售数据的Bayes估计
4 结 论
目前,研究广义非线性模型参数估计问题的方法有很多种,用得较多的是似然估计方法和经验似然估计方法,每种方法都有它们各自的优点.此处则选用了贝叶斯统计分析中蒙特卡洛抽样方法中的M-H抽样算法和Gibbs抽样算法相结合的混合算法进行分析,求出参数的条件后验分布后,根据其分布形式选出合适的算法,抽取每次迭代时的参数值,并利用参数的样本路径图和均值遍历图验证迭代时马尔科夫链的收敛性;收敛后计算参数的后验均值作为估计值,最后通过实证分析比较Bayes估计和极大似然估计的偏差,从而验证M-H抽样算法和Gibbs抽样算法的简洁性、有效性以及可行性.

