不确定中立型变时滞系统基于状态观测器的滑模控制❋
高存臣, 袁雪娇, 张彩虹
(1.中国海洋大学数学科学学院, 山东 青岛 266100; 2.青岛大学自动化与电气工程学院, 山东 青岛 266071)
滑模变结构控制(VSC)方法作为控制理论的一种重要设计方法,应用广泛,例如在制造系统、生物系统、动力系统、车辆飞行器控制等领域均有所涉及。滑模VSC的特性是通过控制量的转换,使被控状态能够沿滑模切换面滑动,并且具有不变性。因此,研究滑模变控制系统具有重要的理论与实际意义。我国学者已经对时滞型、变时滞型、不确定时滞型等系统的VSC问题做了大量研究[1-7]。通过利用Lyapunov泛函法以及线性矩阵不等式(LMI)等技术,得到了时滞系统的稳定条件[8-10]。注意到时滞型、超前型、中立型等泛函微分方程的区别,中立型系统对时间滞后特别敏感,很容易造成系统的不稳定的结果。研究中立型问题相对其他系统复杂一些,因此将滑模变结构思想与系统稳定性联系在一起,将得到更好的动态品质。目前也有一些有关滑模控制下的中立型等系统的研究成果[11-16]。利用VSC研究基于状态观测器下的不确定变时滞中立型系统,是其他文献未涉及的。
在前人研究的基础上,本文研究了在非线性扰动下时变时滞不确定中立系统的具有输入输出的滑模VSC问题,通过构造观测器,以及对误差系统分析,利用Lyapunov泛函法以及线性矩阵不等式(LMI)等技术,得到了系统为渐近稳定的充分条件。
1 系统的描述与相关引理
考虑如下一类不确定中立型变时滞输入输出系统

(1)
其中,x(t)∈Rn为状态向量,u(t)∈Rm为控制输入,f(x(t))为非线性扰动,y(t)∈Rp为系统输出向量,A,A1,B,C0,C,D为相应维数的常数矩阵,τ1>0为常数,φ(t)∈C1([-τ,0];Rn)为初始连续可微向量函数,ψ(t)∈C([-τ,0];Rn)为初始连续向量函数。ΔA和ΔA1为参数不确定函数矩阵,并且满足如下条件:ΔA(t)=EF(t)H1,ΔA1(t)=EF(t)H2,其中,E,H1,H2为已知的相应维数的常数矩阵,F(t)为未知的矩阵函数且满足:
FT(t)F(t)≤I,t∈R+。
(2)
以下是本文用到的假设和引理,保证本文结果的有效性。
假设1 (A,B)为完全可控的;(A,C)为完全可观测的。

假设3 对任意的x1,x2,f(x)满足Lipschitz条件
(3)
其中l>0为Lipschitz常数。
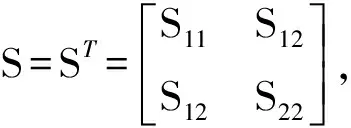
(4)
引理2[5](Jensen不等式)对于任意实矩阵M∈Rm×m,M=MT,标量γ>0,ω:[0,γ]→Rm为可积向量函数,则有如下的积分不等式成立:

(5)
引理3[10]设U,V和W(t)是具有适当维数的实矩阵,并且满足WT(t)W(t)≤I,则对任意实数α>0,以下不等式成立:
UW(t)V+VTWT(t)UT≤αUTU+α-1VTV。
(6)
引理4[17]设X∈Rn,Y∈Rn,则对任意实数α>0,以下不等式成立:
2XTY≤αYTY+α-1XTX。
(7)
2 观测器的设计
为了估计本文所研究的不确定变时滞系统(1)的状态,设计如下非脆弱观测器
(8)
其中:L∈Rn×q为观测器的增益矩阵;ΔL(t)为已知的非线性函数矩阵且满足
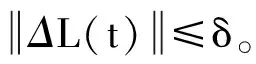
(9)
其中δ>0。
(A-LC+ΔA)e(t)-ΔLCe(t)+
(A1+ΔA1)e(t-τ(t))+
(L+ΔL(t))Dx(t-τ(t))+
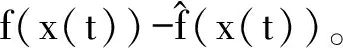
(10)
第一步:构造滑模切换函数
(11)
其中
(12)
此处K为选定矩阵,BTB为非奇异矩阵。
第二步:设计系统(1)的控制输入使得系统(8)中的估计状态能够趋近滑模面。设计合适的滑模控制律如下:
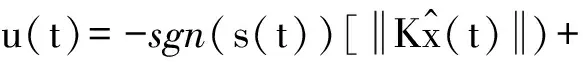
(13)

定理1 如果设计的控制律u(t)为(13)式,那么,系统(8)的运动轨迹会在有限时间内到达滑模面s(t)=0。

(14)


(15)
将(13)代入不等式(15),显然得到

(16)
由Lyapunov 渐进稳定性定理,系统(8)的解将在有限时间内到达滑模面s(t)=0,故定理1得证。
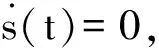
(17)
代入所设计的观测器系统(8)中,得到在估计状态空间中的滑模运动微分方程:
[(PL+ΔL(t))C]e(t)+[P(L+ΔL(t))D]e(t-

(18)
其中P=I-B(BTB)-1BT。因此,可以通过(18)式以及偏差系统(10)来分析我们所要研究的变时滞不确定中立系统(1)的零解稳定性等问题。
定理2 考虑误差系统(10)和滑模动力方程(18),切换函数(11),以及滑模控制律(14),若存在矩阵Q1>0,Q2>0,M1>0,M2>0,M3>0,M4>0,L,Kεi>0,(i=1,2,…,16),满足下面线性矩阵不等式
Ω=
(19)
其中,
Ω11=Q1(A-LC)+(A-LC)TQ1+2l2I+M1+M3+
Ω13=CTLTPTQ2;Ω14=-Q1LD;
(1-h)M1;
Ω23=DTLTPTQ2;Ω25=-(A1-LD)TQ1C0;
Ω26=-DTLTPTQ2C0;Ω36=-(PA-BK)TQ2C0;
[Q2(PA-BK)+(PA-BK)TQ2]+M2+M4+2l2I;
(1-h)M2;
Π1=[Q1E,Q1E,Q1,Q1,Q1,Q1,0,0,0,0,0,0,0,0,0,0,0,0,0,0];
Π2=[0,0,0,0,0,0,Q2P,Q2P,Q2P,Q2,0,0,0,0,0,0,0,0,0,0];
Π5=diag[-ε1I,-ε2I,-ε3I,-ε4I,-ε5I,-I,-ε6I,-ε7I,-ε8I,-I,-ε9I,-ε10I,-ε11I,-ε12I,-ε13I,-I,-ε14I,-ε15I,-ε16I,-I]。
则误差系统(10)和滑模动力系统(18)的零解是渐近稳定的。
注:*代表对称矩阵的相应元素。
证明 构造李雅普诺夫向量函数
(20)
其中,V1(t)=[e(t)-C0e(t-τ1)]TQ1[e(t)-C0e(t-τ1)];
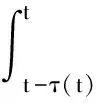

(21)
由(10)、(11)及(21)式,得
2eT(t)Q1[ΔAe(t)+ΔA1e(t-τ(t)]+
2eT(t)Q1(A1-LD)e(t-τ(t))-2eT(t)Q1ΔLCe(t)-
eT(t)M3e(t)-e(t-τ1)TM3e(t-τ1)+
(22)
由引理3和引理4,可得
2eT(t)Q1[ΔAe(t)+ΔA1e(t-τ(t)]≤
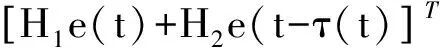
ε3δ2eT(t)CTCe(t)
-2eT(t)Q1ΔLDe(t-τ(t))≤
τ(t)),
τ(t))。
(23)
由假设2.3,又得
eT(t)Q1Q1e(t)+l2eT(t)e(t),
(24)
同理可得
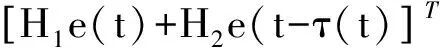
ε12δ2eT(t-τ(t))DTDe(t-τ(t)),
ε14δ2eT(t)CTCe(t),
ε15δ2eT(t-τ(t))DTDe(t-τ(t)),
(25)
类似(23)容易的得到下面不等式
(26)
将 (23)、(24)、(25)、(26)式代入(22)中,得到
(27)
其中
Τ11=Q1(A-LC) + (A-LC)TQ1+


M1+M3,
Τ13=CTLTPTQ2,Τ14= -Q1LD,
(1-h)M1,
Τ23=DTLTPTQ2,Τ25=-(A1-LD)TQ1C0,

Τ36=-(PA-BK)TQ2C0,
(1-h)M2,

注[17]:使用MATLAB中的LMI工具箱求解时,为了简化操作步骤,令Q1=Q2=I。
3 数值算例
考虑误差系统(10)和系统(18)中的矩阵


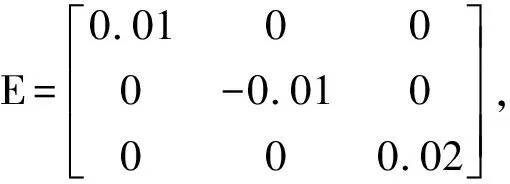
f(x)=0.5sinx,l=0.5,
应用MATLAB中的LMI工具箱求解定理2中的LMI,得到如下结果



ε1=13.479 7,ε2=13.900 4,ε3=6.393 4,
ε4=53.676 9,ε5=55.652 9,ε6=6.353 3,
ε7=53.680 3,ε8=55.652 4,ε9=13.479 5,
ε10=13.900 3,ε11=5.906 6,ε12=53.077 3,
ε13=55.042 4,ε14=5.906 6,ε15=53.077 0,
ε16=55.042 1。

图的轨迹

图2 e(t)的轨迹
因此,该系统是渐近稳定的。
4 结语
本文研究了具有非线性不确定变时滞中立系统的滑模控制,设计了系统的观测器和滑模控制律,并保证了切换面的有限时间可达性,基于线性矩阵不等式技术以及变结构控制理论,得到了误差系统和滑模动力方程的零解渐近稳定性的充分条件,并通过算例说明了本文算法的有效性。

