TIME-PERIODIC ISENTROPIC SUPERSONIC EULER FLOWS IN ONE-DIMENSIONAL DUCTS DRIVING BY PERIODIC BOUNDARY CONDITIONS∗
Hairong YUAN(袁海荣)
School of Mathematical Sciences;Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice,East China Normal University,Shanghai 200241,China E-mail:hryuan@math.ecnu.edu.cn
Abstract We show existence of time-periodic supersonic solutions in a finite interval,after certain start-up time depending on the length of the interval,to the one space-dimensional isentropic compressible Euler equations,subjected to periodic boundary conditions.Both classical solutions and weak entropy solutions,as well as high-frequency limiting behavior are considered.The proofs depend on the theory of Cauchy problems of genuinely nonlinear hyperbolic systems of conservation laws.
Key words supersonic flow;isentropic;compressible Euler equations;duct;time-periodic solution;initial-boundary-value problem
1 Introduction and Main Results
We study the one-space-dimensional isentropic compressible Euler equations(cf.[1,p.31]or[2,p.63])
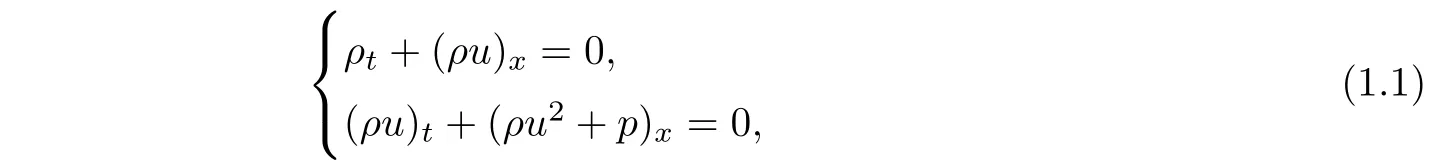
here t>0 represents time,and for a given constant L>0,the space variable x lies in the interval[0,L],which represents a one-dimensional rectilinear duct with constant cross-section and occupied by gas.The unknowns are ρ,p and u,which are respectively the density of mass,scalar pressure,and velocity of the gas flow.We consider isentropic polytropic gas,namely,

with a>0 and γ>1 being constants.The local sonic speed is given by

In this paper,we focus on supersonic flows in the duct;that is,u(t,x)>c(t,x)for t>0 and x∈[0,L].Suppose the gas flow is uniform initially
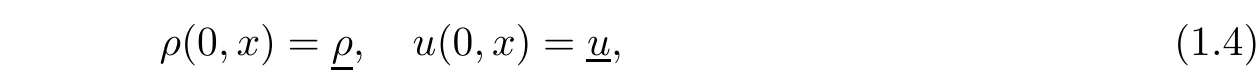
where ρ >0,u>0 are constants and.To control the flow,we propose the boundary conditions
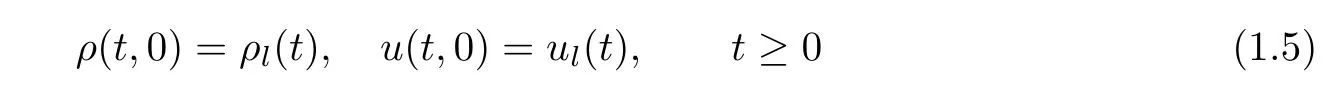
at the in flow boundary{x=0}.The problem is,if ρl,ulare periodic functions(i.e.,there is a constant P>0 so that ρl(t+P)= ρl(t),ul(t+P)=ul(t)for all t>0)andcan we obtain a periodic solution of the initial-boundary-value problem(1.1)(1.4)(1.5)?
We will prove the following three theorems.
Theorem 1.1(Classical solutions) Suppose that ρl(t)and ul(t)are periodic functions with a period P>0 and ρl(0)= ρ,ul(0)=u.There are positive constants ε0,T0and C0such that if
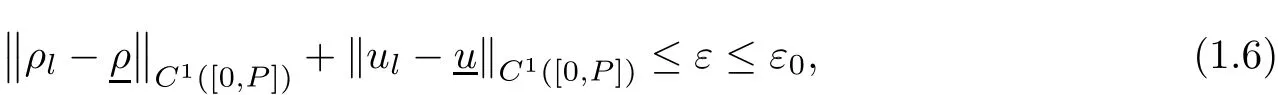
then there is a unique Lipschitz continuous solution(ρ,u)to problem(1.1)(1.4)(1.5),which is C1for t>T0,and satis fies that
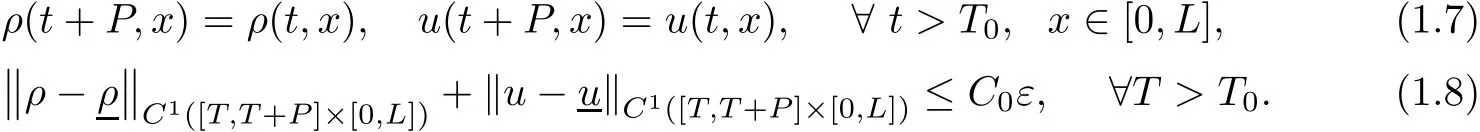
A weak solution to problem(1.1)(1.4)(1.5)is de fined in the standard way via integration by parts after multiplying a test function inwhose support does not meet the line{x=L},cf.[2,Section 4.3,p.82]or[3,De finition 2.1,p.7].A weak solution satisfying the following well-known Lax E-condition[2,(8.3.7)in p.274]is called a weak entropy solution
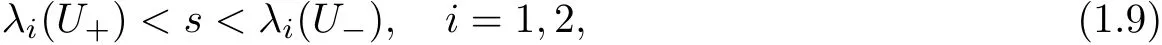
here λ1=u − c,λ2=u+c are characteristics of system(1.1);s is the speed of a shock-front,and U−(U+)is the state of the gas on the left-hand(right-hand)side of the shock-front(here as usual the x-axis is placed horizontally;its positive direction is from the left-hand side to the right-hand side.The positive direction of t-axis is upward).From Theorem 8.5.3 in[2,p.283],we know that for our situation,such weak entropy solutions also satisfy the entropy admissability condition based on entropy-entropy flux pair(see[2,p.85]).
Theorem 1.2(Weak solutions) Suppose that ρl(t)and ul(t)are periodic functions with a period P>0.There are positive constants ε0,T0and C0,such that if
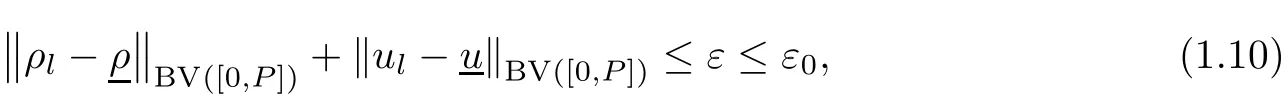
where k·kBV(A)is the bounded variation norm of a single-variable function on a set A,then there is a unique weak entropy solution(ρ,u)to problem(1.1)(1.4)(1.5),which satis fies that
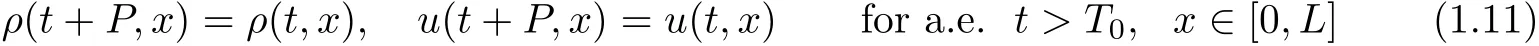
and
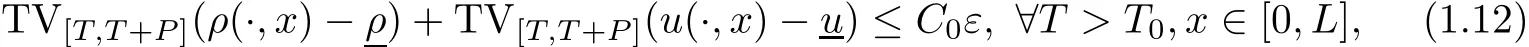
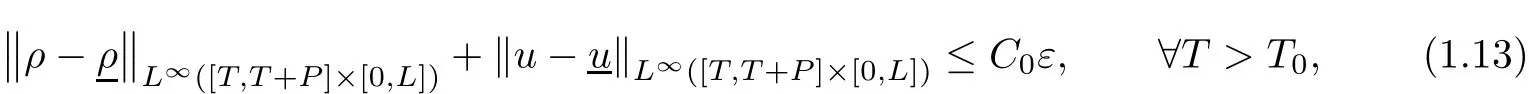
here TVA(·)means total variation of a function on the set A.
Remark 1.3Due to the finite speed propagation of signals in hyperbolic systems,the appearance of the start-up time T0needed for the boundary conditions to e ff ect in the whole duct is natural.We also note that T0depends only on L and a bound of the characteristic speed of the Euler system,as can be seen easily from the proof of these theorems.
Theorem 1.4(High-frequency limit) Suppose that ρl(t)and ul(t)are given bounded periodic functions with a period P>0.There are positive constants ε0such that if
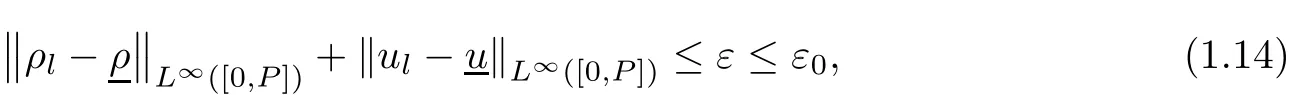
then for any positive number ω,there is a weak entropy solution(ρω,uω)to(1.1),(1.4),subjected to the boundary conditions
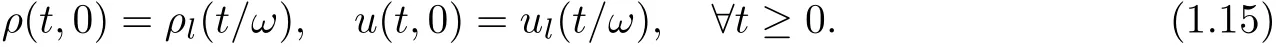
There are positive constants T0,C0so that the solution satis fies
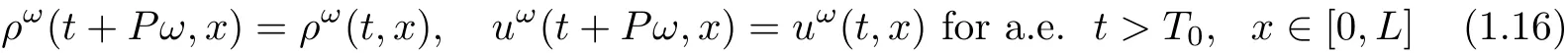
and
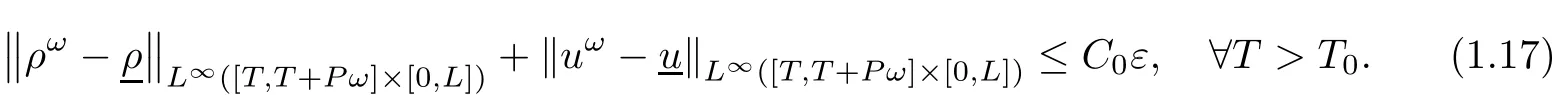
Furthermore,it holds that
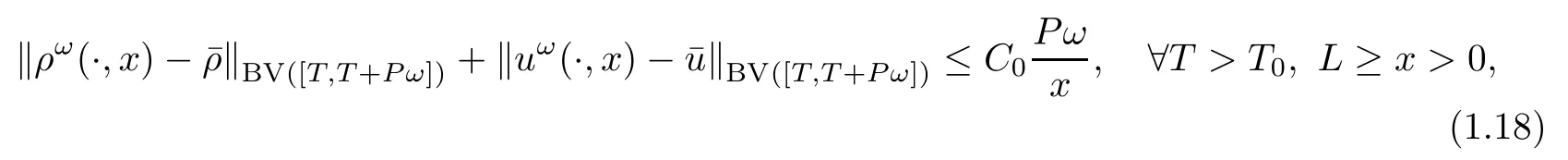
and particularly,
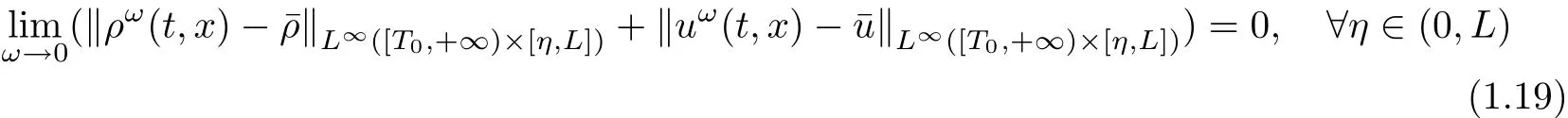
with
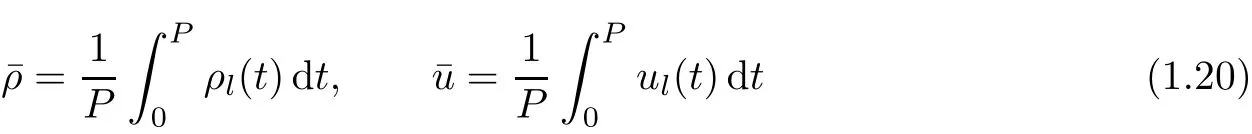
being the averages of ρl,ulover a period.
Remark 1.5Comparing to Theorem 1.2,under the weaker assumption(1.14),we do not claim uniqueness of weak entropy solutions in Theorem 1.4,which is an open problem in the theory of hyperbolic systems of conservation laws.Estimates(1.18),(1.19)demonstrate homogenization in the domain realized by high-frequency,small-amplitude perturbations from the boundary conditions.
In the following Sections 2–4,we prove the above three theorems,by reducing to several Cauchy problems of hyperbolic systems.
There are several reasons why we are interested in time-periodic solutions of Euler equations in ducts,driving by periodic boundary conditions.The main motivation is to understand better some interesting physical phenomena related to periodic motions of fluids in nozzles,see for example,[4],where the authors carried out experiments,trying to control a normal shock to move periodically in a tube,by adjusting the boundary conditions acting at the exit of the tube,while the supersonic flow ahead of the normal shock remained unchanged.It turns out that the mathematical analysis is quite challenging.Up to now there are many impressive progress on the studies of periodic solutions of partial di ff erential equations arising from fluid dynamics,when viscosity,damping,or certain other dissipation e ff ects were taken into account,see,for instance,[5–10]and references therein.However,except the piston problems considered for viscous flows in[9,10],most of the works considered time-periodic solutions driving only by time-periodic external forces.As known in control theory,it is usually harder to realize periodic motion just by boundary control.There are fewer works on periodic solutions of hyperbolic conservation laws,while most of them concentrate on space-periodic solutions[11–18].See[19,20]for some results on the case of time-periodic solutions driving by time-periodic external forces.To our knowledge,it seems that there is no previous result on time-periodic solutions of hyperbolic conservation laws induced by time-periodic boundary conditions.There are so many interesting open problems in this direction,and our investigations of periodic motions of subsonic flows and transonic shocks in nozzles will be reported in other papers.
2 Classical Solutions
For classical solutions,system(1.1)admits the Riemann invariants[1,p.32]

and(1.1)is equivalent to the following diagonal system

where

are characteristics of system(1.1),and are both positive for supersonic flows.In an obvious way,the initial data and boundary conditions can be written respectively as
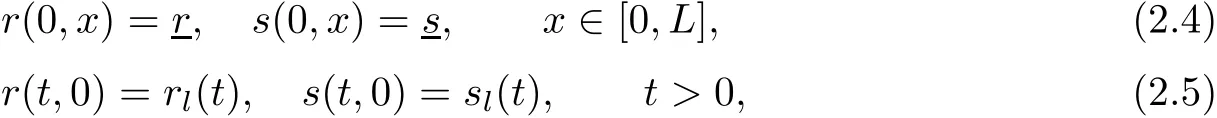
here r,s are constants,and rl(t),sl(t)are periodic functions with the period P.
We now interchange the role of t and x,and consider the following Cauchy problem in the direction x>0,while t∈R,

The compatibility condition required in Theorem 1.1 implies that the “initial data” r∗and s∗are Lipschitz continuous and C1,except at t=0.Then Theorem 7.2 in[1](with α =0)guarantees that for given L>0,there is a constant ε0of the order 1/L,so that the above problem(2.6)admits a unique classical solution(r,s),provided that
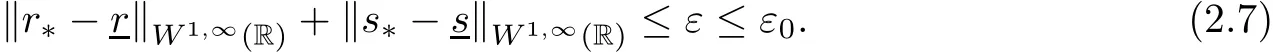
Furthermore,it holds that
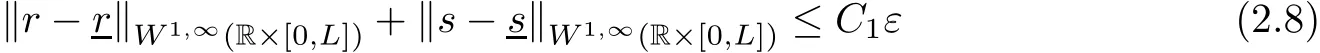
for a constant C1depending only on ρ,u,γ and L.By the characteristic method,it is easily seen that the solution(r,s)restricted on(0,∞)× [0,L]is a classical solution to problem(2.2)(2.4)(2.5).Since ε0is chosen small,we conclude that the flow is still supersonic,and

What left is to show that for

there holds
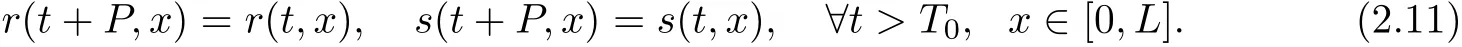

Then Ux+ΛUt=0,and
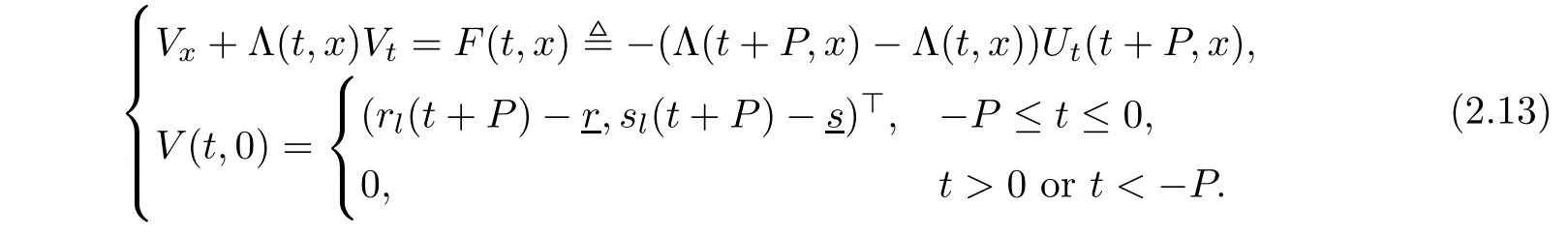
Notice that λ1(r,s), λ2(r,s)are Lipschitz continuous functions of(r,s),simple computation and(2.8)yield the estimates
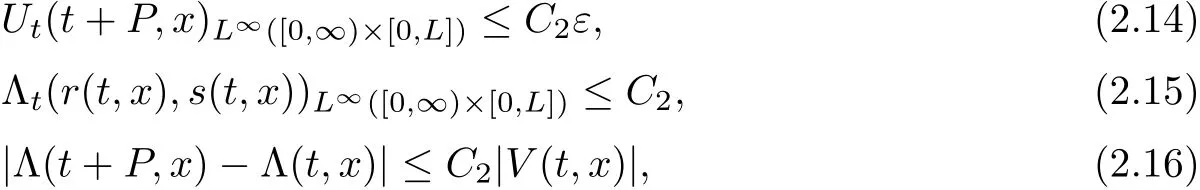
where C2>0 depends only on ρ,u and γ,L.It follows that

Now fix a point(t′,x′)with t′>T0,0 and for 0 For x ∈ (0,x′),set Then since t′>T0and x′∈ [0,L],by de finition of T0,it follows from uniqueness of solutions of Cauchy problems of ordinary di ff erential equations that(t1(0),t2(0))⊂(0,+∞),and by(2.13),V(t,0)≡0 there.Hence Taking derivative with respect to x,we also have In the last inequality we used(2.15)and(2.17).So by Gronwall’s inequality,we infer that I(x) ≡ 0.Particularly,by continuity of V(t,x),we see V(t′,x′)=0.This proves(2.11). Since ρland ulare C1as we assumed in(1.6),by the above choice of T0and characteristic method,we see that the solution is actually C1for t>T0,0≤x≤L;and one may replace the W1,∞norm in(2.8)by C1norm to obtain(1.8).The proof of Theorem 1.1 is completed. Set m= ρu,n= ρu2+p.Then,and since u>c,by implicit function theorem,we could solve ρ=f(m,n).Hence the equations(1.1)could be written as It is easy to check that this system,taking x as “time”,is strictly hyperbolic and genuinely nonlinear,with eigenvalues 1/(u+c)and 1/(u−c). Now de fine Then de fine where[k]means the largest integer that is smaller than or equal to k. Now we study a Cauchy problem of(3.1)with the initial data here IA(·)is the characteristic function of the set A:IA(t)=1 if t∈ A and IA(t)=0 otherwise.By either methods of vanishing viscosity or wave front tracking(cf.Theorem 15.1.1 in[2,p.557]),we know there is a constant ε0such that if(1.10)holds,then there is a unique global weak entropy solution(m,n)∈ L∞((−∞,+∞)×[0,+∞))that is of bounded variation in t-variable for each fixed x>0, Also,the solution lies in Bδ0(ρ,u).These lead to estimates(1.12),(1.13). For simplicity of writing,we set U(t,x)=(m(t,x),n(t,x))⊤,andŪ(t,x)=U(t+P,x).Then by(15.8.10)or(15.8.11)in[2,p.581](see also(13.13)in[21,p.294]),we have,for arbitrary a for some positive constant M depending only on ρ,u and γ,δ0.By(3.6),(3.7),one has We note by de finition of weak solutions,a weak solution to problem(3.1)–(3.3)is also a weak solution to problem(1.1)(1.4)(1.5).Since the solution constructed above for problem(3.1)–(3.3)satis fies the Lax E-condition(observing that the orientation of(x,t)-coordinates is opposite to the(t,x)-coordinates) it also satis fies the Lax E-condition(1.9)for problem(1.1)(1.4)(1.5).We remark that the positiveness of λ1,λ2,namely,the flow is supersonic,is crucial here.For more general results on equivalence of weak solutions of hyperbolic conservation laws by interchanging the role of t and x,one may refer to Lemma 2.12 in[3,p.14]. This establishes existence of weak entropy solutions that are time periodic for t>T0,to problem(1.1)(1.4)(1.5).We may take.Uniqueness follows directly from the L1stability estimate(3.9). Let Ul(t)be a given bounded periodic function for t≥ 0 with period P>0,and ω a positive number.We now consider the following problem where,following notations in the previous section,U=(m,n)⊤and F(U)=(f(m,n),m)⊤.A solution of this problem will be denoted as Uω.We wish to understand limiting behaviour of Uωas ω ↓ 0. where By the assumptions in Theorem 1.4,we havefor a constant C depending only on the Euler system.Thanks to Theorem 5.1 in[15,p.95],problem(4.2)has a weak entropy solutionfor any ω>0.Then by applying the method of generalized characteristics as in[15](see also[2,Chapter X]),with similar arguments of the previous section,by restricting the solution to 0 We consider the asymptotic behaviour of Uω(t,x)as ω →0,where t>T0,and 0 Then V solves Hence,we are led to consider the Cauchy problem Thanks to Theorem 5.2 in[15,p.109],not only does V exist as a periodic function in τ-variable with period P,but also it satis fies the estimates for a generic constant H1depending only on U and γ.Here we have setto be the average ofover an interval with length P.It follows immediately that,for any x∈(0,L], These inequalities lead easily to the estimates claimed in Theorem 1.4.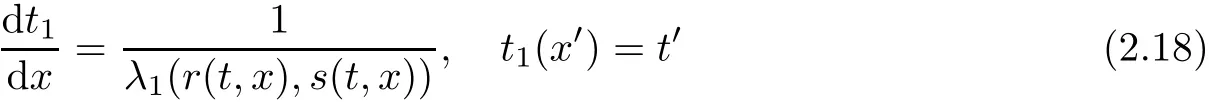

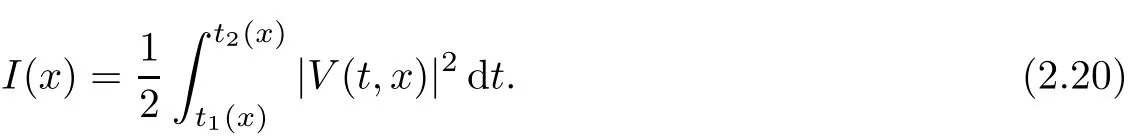

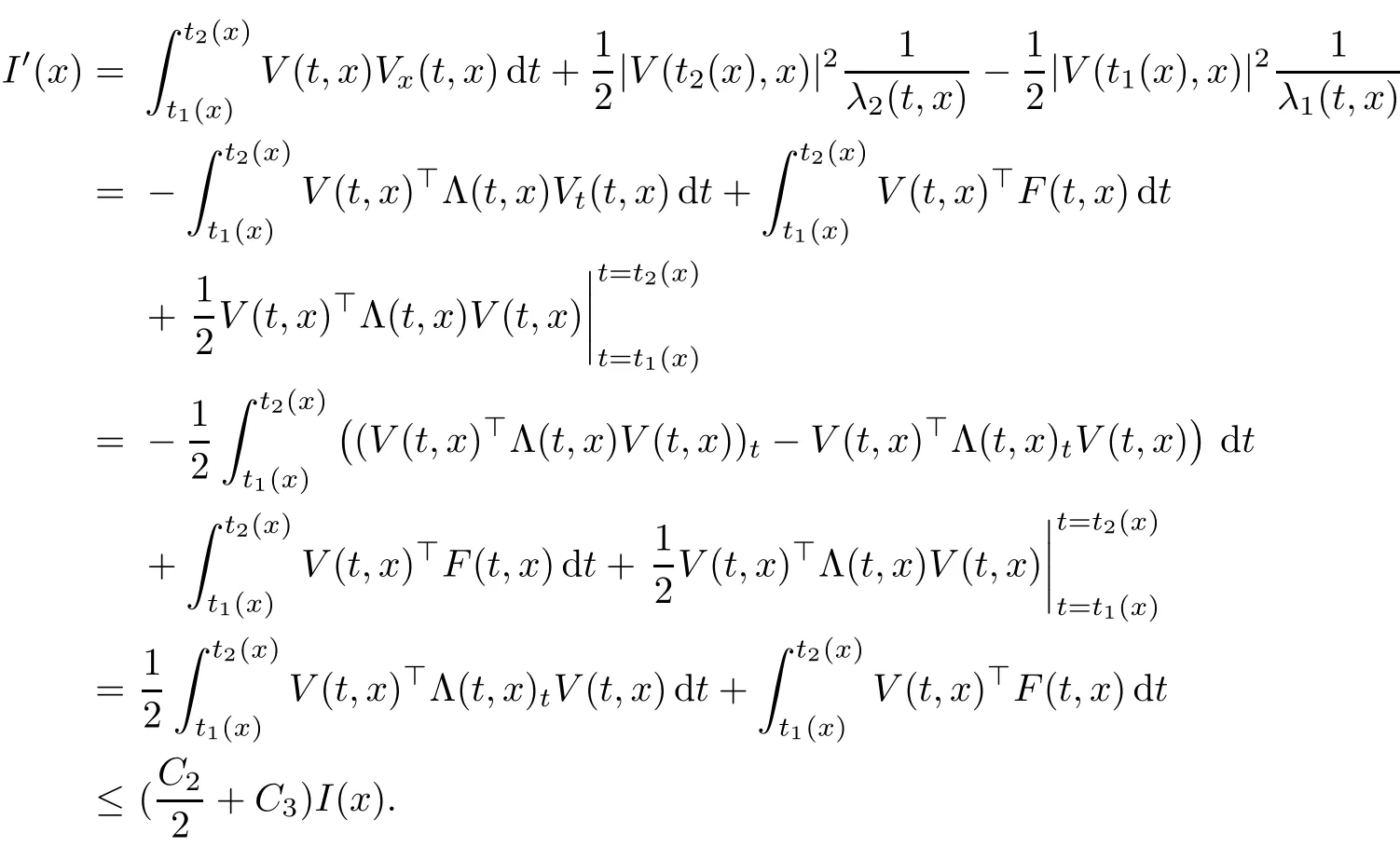
3 Weak Solutions

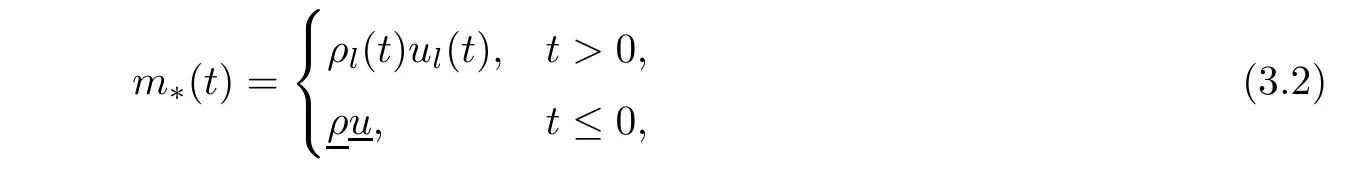
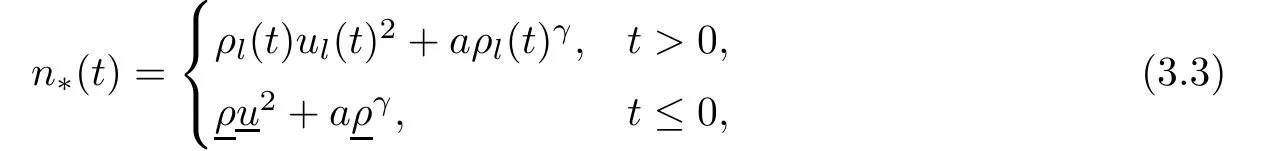
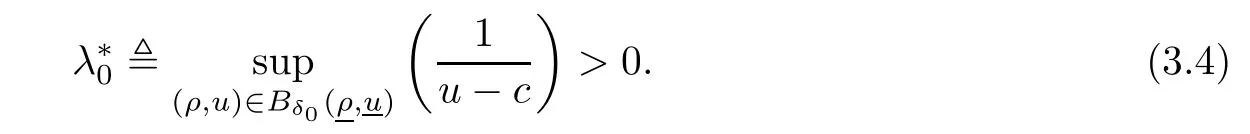

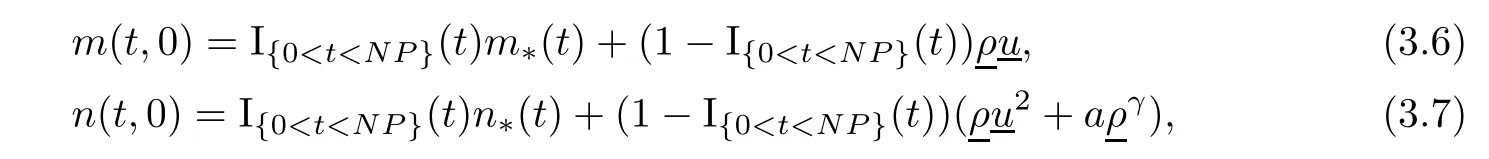
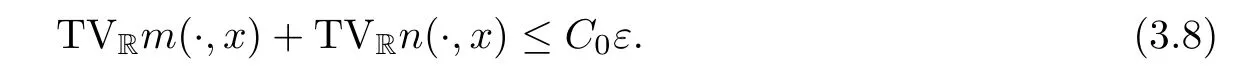
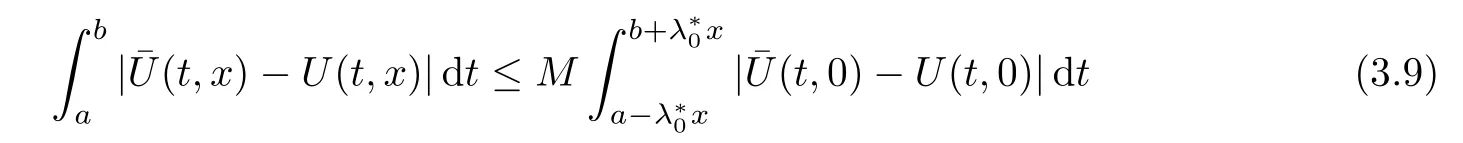
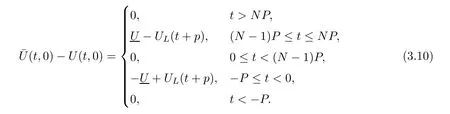
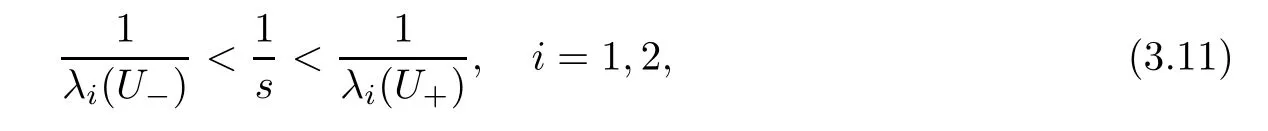
4 High-Frequency Limit
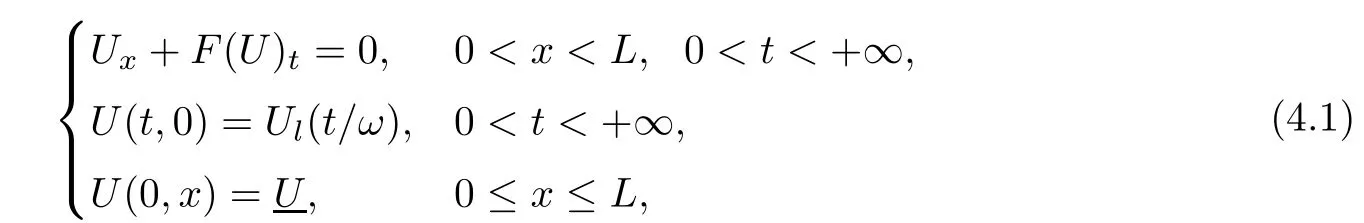


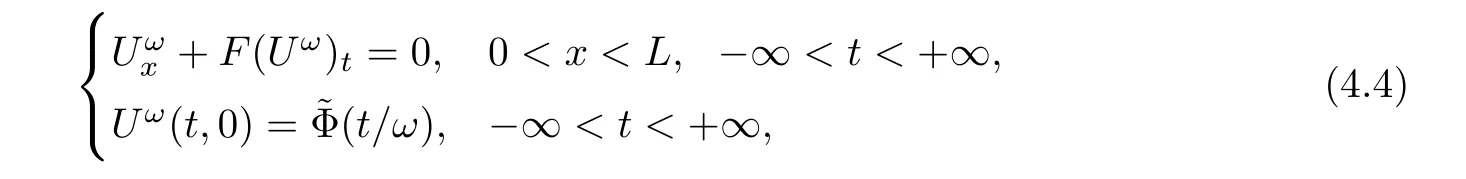
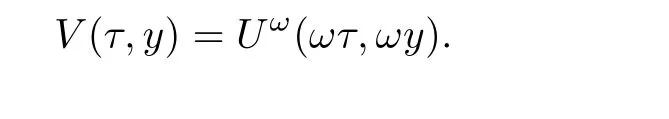
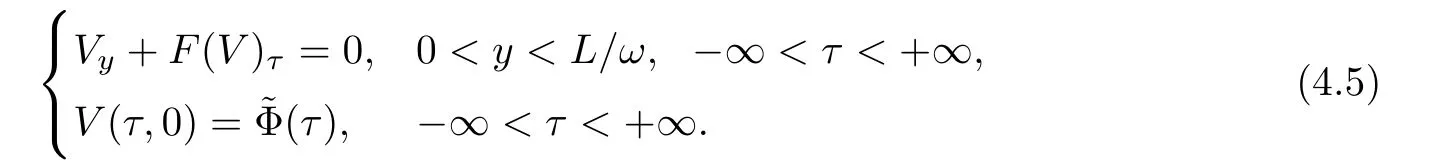
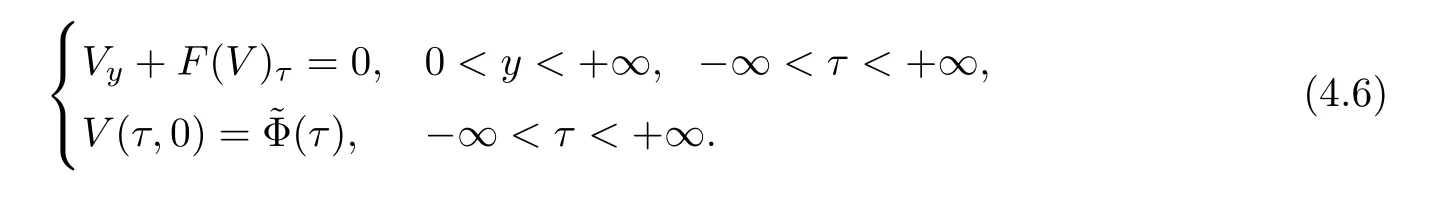
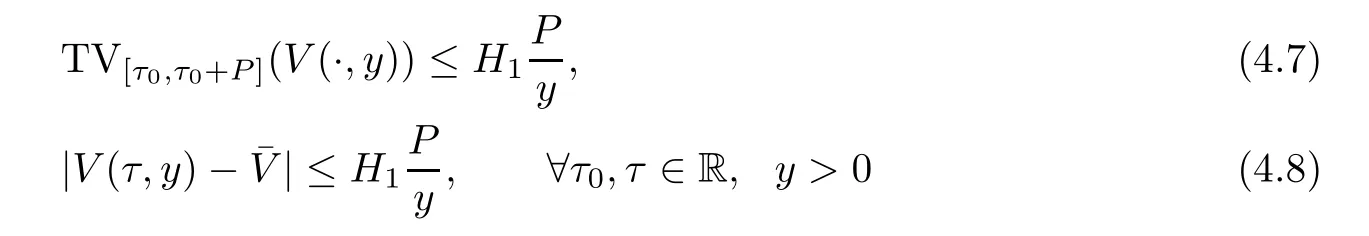
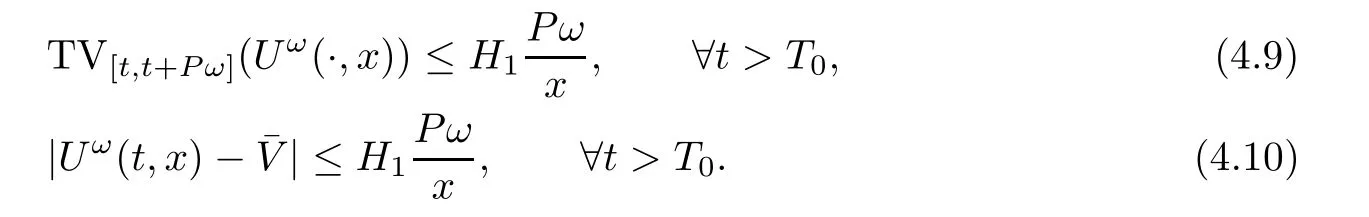
 Acta Mathematica Scientia(English Series)2019年2期
Acta Mathematica Scientia(English Series)2019年2期
