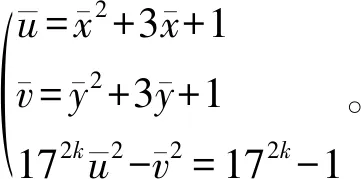不定方程172kx(x+1)(x+2)(x+3)=y(y+1)(y+2)(y+3)的整数解
张 敏,高 丽
(延安大学数学与计算机科学学院,陕西延安716000)
不定方程的求解问题不仅在数论中具有重要的研究价值,而且在其它学科中也有广泛的应用价值,如在密码学、电子工程和计算机科学技术等方面都有重要的应用。因此不少学者对其进行了深入系统的研究,如四次不定方程
Mx(x+1)(x+2)(x+3)=
Ny(y+1)(y+2)(y+3)
(1)
其中M,N为整数。
1971年,Cohn J E[1]证明了当M=2,N=1时,不定方程(1)只有正整数解(x,y)=(5,4);1975年,Ponnudurai T[2]证明了当M=3,N=1时,不定方程(1)有正整数解(x,y)=(3,2)和(7,5);1982年,宣体佐[3]证明了当M=5,N=1时,不定方程(1)只有正整数解(x,y)=(2,1);1991年,罗明[4]证明了当M=1,N=7时,不定方程(1)只有正整数解(x,y)=(4,2);2006年,柳杨[5]证明了当M=112k,N=1时,不定方程(1)没有正整数解;2007年,柳杨等[6]证明了当M=132k,N=1时,不定方程(1)没有正整数解;2011年,徐凯等[7]证明了当M=192k,N=1时,不定方程(1)没有正整数解;2009年,罗明等[8]证明了当M=3,N=5时,不定方程(1)只有正整数解(x,y)=(7,6);同年段辉民等[9]证明了当M=1,N=19时,不定方程(1)没有正整数解;2015年,张洪等[10]证明了当M=1,N=21和M=1,N=23时,不定方程(1)没有正整数解;2016年刘海丽等[11]证明了M=1,N=35时,不定方程(1)只有正整数解(x,y)=(4,1);同年林昌娜等[12]证明了M=1,N=34时,不定方程(1)只有正整数解(x,y)=(14,5);张洪[13]讨论不定方程(1)的正整数解情况;2017年,胡邦群等[14]证明了M=6,N=7时,不定方程(1)只有正整数解(x,y)=(25,24);2018年,陈琼[15]证明了M=1,N=33时,不定方程(1)只有正整数解(x,y)=(9,3);白金卉[16]证明了M=1,N=37时,不定方程(1)没有正整数解。
本文就是在以上研究思路以及方法的基础上,对M=172k,N=1这一种情形做了进一步研究,证明如下定理:
定理当M=172k,N=1(k∈N)时不定方程(1)没有正整数解,即不定方程
172kx(x+1)(x+2)(x+3)=
y(y+1)(y+2)(y+3)
(2)
没有正整数解。
1 预备引理
为证明这一定理,我们需要先做一些准备工作。
引理1 当M=172k,N=1(k∈N)时,不定方程(2)有正整数解的充要条件是不定方程组
(3)
有正整数解。
证明:必要性 若方程(2)有正整数解x0,y0,则
172kx0(x0+1)(x0+2)(x0+3)=
y0(y0+1)(y0+2)(y0+3)。
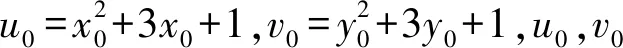
(v0-1)(v0+1)=172k(u0-1)(u0+1),

这表明不定方程组有正整数解u0,v0,x0,y0。
充分性 若不定方程组(3)有正整数解u0,v0,x0,y0,则
从而可得
即172kx0(x0+1)(x0+2)(x0+3)=
y0(y0+1)(y0+2)(y0+3),
由此可知,方程(2)有正整数解x0,y0。
引理2 设k为自然数,则不定方程组
(4)
仅有一组正整数解:
u=1,v=1,A=17k-1,B=17k+1。
证明:由A=17ku-v,B=17ku+v可知A<17k,B>17k,则A 于是可知,1≤A<17k 令A=17k-l1,1≤l1<17k,l1是整数;B=λ17k+l2,λ≥1,0≤l2<17k,λ,l2均为整数。则方程组(4)的前两式可化为 即2×17ku=17k(λ+1)+(l2-l1),由此可知17k|(l2-l1),又因为0≤|l2-l1|<17k,因此必有l2-l1=0。令l2=l1=l,1≤l<17k,则有 A=17k-l,B=λ17k+l, 由AB=172k-1及上式得 172k-1=(17k-l)(λ17k+l)= 172kλ+17kl-17kλl-l2,即 17k(λ-1)(17k-l)=(l-1)(l+1) (5) 若λ=1,则有l=1,从而可得A=17k-1,B=17k+1,此时方程(4)有正整数解u=1,v=1,A=17k-1,B=17k+1。 若λ>1,则l>1,此时有2u=λ+1,由此可知λ为奇数,由式(5)可知17k|(l+1)(l-1)。 若17k|(l+1),且有17k|(l-1),则有17|[(l+1)-(l-1)],故与17⫮ 2互相矛盾,这表明17k|(l+1),1≤l<17k,所以必有l+1=17k,将l+1=17k代入A=17k-l中,并利用AB=172k-1可知A=1,B=172k-1,与题设矛盾。 所以不定方程组(4)仅有一组正整数解: u=1,v=1,A=17k-1,B=17k+1。 引理3 当k是自然数,则不定方程 172ku2-v2=172k-1 仅有正整数解u=1,v=1。 证明:由引理2即可以得到引理3的结论。2 定理的证明