一种基于相对信息粒度的属性约简算法∗

孙 敬

（1.湖北工业大学理学院 武汉 430068）（2.郑州工业应用技术学院信息工程学院 郑州 451100）

1 引言

属性约简是粗糙集理论的主要研究内容之一，寻找高效属性约简算法一直是学者关注的焦点［1～2］。目前，许多学者先后从强化正域［3］、条件熵［4～5］、互信息［6］、区分矩阵［7～8］、粒计算［9～12］、知识粒度［13］、决策重要度［14］、遗传粒子群［15］、加权浓缩树［16］等方面提出了自己的方法。但是，这些算法虽然比较了不同属性集的各方面能力，却容易忽略知识本身之间的关系。本文将利用粒计算理论，从信息粒库出发，运用粒之间的运算计算对应的相对信息粒度，据此提出一种基于相对信息粒度的属性约简改进算法。

2 相对信息粒度与属性约简

2.1 信息粒库

定义 1［1］设四元组 S=（U，C∪D，V，f）为决策信息系统，其中U 为非空有限的对象集合；C 为条件属性集，D 为决策属性集，且C∩D=Ø，D≠Ø；V=∪a∈AVa，其中 Va为某属性 a 的值域；f 为 U×C∪D→V 的信息函数，即对任意的a∈C∪D，x∈U，均有 f（x，a）∈Va。

定义2 设S=（U，C∪D，V，f）为一个决策信息系统，令 a∈C∪D，v∈Va，则称（a，v）或av为 S 上原子公式。令 m 为 S 上的粒函数，其中 m（av）=｛x | f（x，a）=v，a∈C∪D，x∈U｝，则称 Gr（a）=（av，m（av））为S上关于属性a的一个原子粒。

定义3 设S=（U，C∪D，V，f）为一个决策信息系统，设φ、ψ为S 上有限个原子公式利用联结词（∧）构成的两个复合公式，令m（φ）、m（ψ）为满足公式φ、ψ的对象集合，则称 Gr（φ）=（φ，m（φ））、Gr（ψ）=（ψ，m（ψ））分别为S 上关于φ、ψ的复合粒，且Gr（φ）∧Gr（ψ）=（φ，m（φ））∧（ψ，m（ψ））=（φ∧ψ，m（φ）∩m（ψ））。

为了更好地从语法和语义方面刻画属性与对象之间的关系，借助粒计算理论，下面给出由复合公式和粒函数所确定的信息粒库的定义。

定义4 设S=（U，C∪D，V，f）为一个决策信息系统，P⊆C 且 P=｛p1，p2，…，pn｝（n 为 P 的属性个数），vi∈Vp1×Vp2×…×Vpn，令公式集φp=｛Pvi|Pvi=（p1，v1i）∧（p2，v2i）∧…∧（pn，vni），vi1∈Vp1，vi2∈Vp2，…，vin∈Vpn，i=1，2，3，…｝，令

则称 Gr（P）为 P 对应的 n 阶信息粒库，（Pvi，m（Pvi））为Gr（P）一个n阶信息粒。

由定义 4 可知，Gr（P）用公式 Pvi从语法角度阐述了粒的产生规则，m（Pvi）从语义角度阐述了粒的构成对象。

定义5 设S=（U，C∪D，V，f）为一个决策信息系统，P、Q⊆C，Gr（P）、Gr（Q）为P、Q的信息粒库，若对 ∀（Pvi，m（Pvi））∈Gr（P），均存在一个（Qvi，m（Qvi））∈Gr（Q），使得m（Qvi）⊆m（Pvi），则称Gr（Q）比Gr（P）粒化更细，记为Gr（Q）⊆Gr（P）。

定理1 设S=（U，C∪D，V，f）为一个决策信息系统，若P⊆Q⊆C，相应的信息粒库为Gr（P）、Gr（Q），则有Gr（Q）⊆Gr（P）。

证明:令 P=｛p1，p2，…，pn｝（n 为 P 的属性个数），由于 P⊆Q，则知 Q 比 P 的属性个数多，令 Q=｛p1，p2，…，pn，pn+1，pn+2，…，pn+m｝（假设pn+1，pn+2，…，pn+m为Q比 P 多的 m 个属性），对于任意的 m（Qvi）=m（（p1，v1i）∧（p2，v2i）∧…∧（pn，vni）∧（pn+1，vn+1i）∧（pn+1，vn+1i）∧…∧（pn+m，vn+mi））=m（p1，v1i）∩m（p2，v2i）∩…∩m（pn，vni）∩m（pn+1，vn+1i）∩m（pn+1，vn+1i）∩…∩m（pn+m，vn+mi）⊆m（p1，v1i）∩m（p2，v2i）∩…∩m（pn，vni）=m（（p1，v1i）∧（p2，v2i）∧…∧（pn，vni））=m（Pvi），又知m（Qvi）是任选的，由定义5知Gr（Q）⊆Gr（P）。

特别地，若 P=Q，则由定理 1 可知 Gr（Q）=Gr（P），此时称Gr（P）、Gr（Q）粒化相同。

2.2 相对信息粒度

定义6 设S=（U，C∪D，V，f）为一个决策信息系统，P⊆C，对任意的（Pvi，m（Pvi））∈Gr（P）、（Dvj，m（Dvj））∈Gr（D）（i=1，2，3，…，m，j=1，2，3，…，n，m、n分别为Gr（P）、Gr（D）的公式个数），令

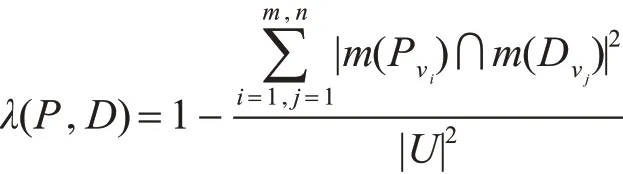
则称λ（P，D）为 P 关于D 的相对信息粒度，|·|是某个集合的元素个数。

由相对信息粒度定义可知，λ（P，D）反映的是属性集P 关于D 的粒化论域能力，显然0 ≤λ（P，D）≤1。λ（P）值越大，说明该属性集的粒化能力越强，否则，粒化能力就越弱。

定理2 设S=（U，C∪D，V，f）为一个决策信息系统，P⊆Q⊆C，则有λ（P，D）≤ λ（Q，D）。

证明:由于P⊆Q，由定理1 知Gr（Q）⊆Gr（P），则存在一个（Qvi，m（Qvi））∈Gr（Q），使得m（Qvi）⊆m（Pvi）（i=1，2，3，…），可知m（Qvi）∩m（Dvj））⊆m（Pvi）∩m（Dvj））（j=1，2，3，…，n，n为Gr（D）的公式个数），由定义6可知，λ（P，D）≤ λ（Q，D）。

由定理2 可知，属性集属性个数越多，其对应的信息粒库粒化能力越强，属性集关于D的相对信息粒度值就越大，特别地，若P=Q，由定理2 可知，λ（P，D）= λ（Q，D），显然，这两个属性集的粒化能力相同。

2.3 属性重要度与属性约简

定义7 设S=（U，C∪D，V，f）为一个决策信息系统，对任意属性a∈C，令

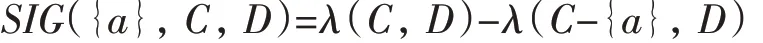
则称 SIG（｛a｝，C，D）为属性a 关于D 相对于C的属性重要度。其中，λ（C，D）、λ（C-｛a｝，D）分别代表C、C-｛a｝关于D的相对信息粒度。

由定义7可知，SIG（｛a｝，C，D）衡量的是删除属性a 后引起的C 关于D 的相对信息粒度变化情况，显然0 ≤ SIG（｛a｝，C，D）≤ 1。当SIG（｛a｝，C，D）=0时，则知λ（C，D）-λ（C-｛a｝，D）=0，即λ（C，D）=λ（C-｛a｝，D），说明删除属性a 后C 关于D 的相对信息粒度并未发生变化，属性a 在C 中是不重要的，或称冗余的。

性质1 对任意属性a∈C，它是C 中必要属性当且仅当SIG（｛a｝，C，D）＞0。

性质 2 核集 COREC（D）=｛a∈C| SIG（｛a｝，C，D）＞0｝。

定义8 设S=（U，C∪D，V，f）为一个决策信息系统，P⊆C，对任意属性a∈P，若SIG（｛a｝，C，D）＞0，则称P是独立的。

由于以核为起点的启发式属性约简中，需要不断地往核集中添加属性，所以下面给出另外一种属性重要度的定义。

定义9 设S=（U，C∪D，V，f）为一个决策信息系统，P⊆C，对任意属性a∈C-P，令

SIG（｛a｝，P∪｛a｝，D）=λ（P∪｛a｝，D）-λ（P，D）

则称SIG（｛a｝，P∪｛a｝，D）为非P 属性a 关于D相对于P的属性重要度。其中，λ（P∪｛a｝，D）、λ（P，D）分别代表P∪｛a｝、P关于D的相对信息粒度。

由定义9可知，SIG（｛a｝，P∪｛a｝，D）衡量的是添加非P属性a后引起的P关于D的相对信息粒度变化情况，显然0 ≤ SIG（｛a｝，P∪｛a｝，D）≤ 1，SIG（｛a｝，P∪｛a｝，D）值越大，说明非P属性a对P越重要。

定理3 设S=（U，C∪D，V，f）为一个决策信息系统，P⊆C。若P 是独立的且λ（P，D）=λ（C，D），则称P为C相对于D的一个约简。

2.4 基于相对信息粒度的属性约简算法

该算法需要先从条件属性集中选出必要属性组成核集作为初始约简集，然后在该集合中不断添加属性重要度最大的属性，循环判断当前约简集是否满足定理3 中约简的要求，直至算法结束。下面给出本文基于相对信息粒度的属性约简算法。

输入:一个决策信息系统S=（U，C∪D，V，f）。

输出:决策信息系统的约简Red（S）。

步骤1:计算λ（C，D），令Red（S）=COREC（D）；

步骤2:判断λ（Red（S），D）=λ（C，D）是否成立，若成立，则跳转到步骤4，否则跳转到步骤3；

步骤3:对于任意a∈C-Red（S），计算其属性重要度 SIG（｛a｝，Red（S）∪｛a｝，D），令 Red（S）=Red（S）∪｛a｝，其中属性a为所有C-Red（S）中属性重要度最大的属性（若多个属性值最大，任选一个加入Red（S）），执行步骤2；

步骤4:算法结束，输出约简Red（S）。

3 实例分析

利用文献［1］中的一个决策信息系统（表1），下面将验证本文算法的有效性。其中，U=｛x1，x2，x3，x4，x5，x6｝，C=｛a，b，c｝，D=｛d｝，利用文献［1］得到的约简为｛ab｝或｛ac｝。

结合上述决策信息系统，下面给出本文属性约简算法的具体执行过程，以此来验证本算法的有效性。

首 先 ，计 算 λ（C，D）。 Gr（C）∩Gr（D）=｛（（a2b2c0d1），｛x1｝），（a1b2c0d0），｛x2｝），（a1b2c0d1），｛x3｝），（（a0b0c0d0），｛x4｝），（（a1b0c1d0），｛x5｝），（a2b0c1d1），｛x6｝）｝，所以 m（C）∩m（D））=｛｛x1｝，｛x2｝，｛x3｝，｛x4｝，｛x5｝，｛x6｝｝，λ（C，D）=1-1/6=5/6。对任意的 a∈C，逐一计算 SIG（｛a｝，C，D），可得 SIG（｛a｝，C，D）=5/6-7/9=1/15，SIG（｛b｝，C，D）=SIG（｛c｝，C，D）=5/6-5/6=0，COREC（D）=｛a｝，令Red（S）=COREC（D）=｛a｝。

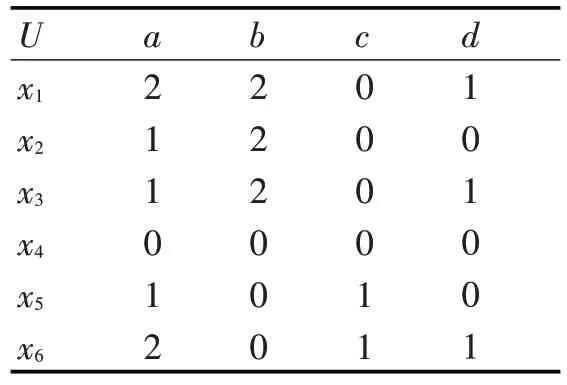
表1 决策信息系统S

判断当前约简集是否满足条件λ（Red（S），D）=λ（C，D）。由于λ（Red（S），D）= λ（｛a｝，D）=13/18≠5/6=λ（C，D），所以对任意的b∈C-Red（S），计算SIG（｛a｝，Red（S）∪｛a｝，D），可得 SIG（｛b｝，｛a｝∪｛b｝，D）=SIG（｛c｝，｛a｝∪｛c｝，D）=5/6-13/18=1/9＞0，按步骤3任选属性b加入约简集中，即Red（S）=｛ac｝。

对于Red（S）=｛ac｝，判断λ（Red（S），D）=λ（C，D）是否成立。由于λ（｛ac｝，D）=λ（C，D）=5/6，条件成立，转向步骤4，算法结束，输出约简集Red（S）=｛ac｝。

同样，可验证｛ab｝也是该决策信息系统的约简，这与文献得到的约简集是一致的，说明该算法是有效的。

4 结语

本文依托粒计算理论，从原子粒和复合粒出发，介绍了信息粒库的概念，据此给出了相对信息粒度来度量某属性集关于决策属性集的相对粒化能力，并提出了一种基于相对信息粒度的属性约简算法，结合实例分析为决策信息系统属性约简提供了一种新的研究方法。