基于压缩控制点的B样条曲线重构算法
任利娟,张广鹏,王 元,王妮娜,黄玉美
(西安理工大学机械与精密仪器工程学院,陕西西安710048)
逆向工程是机械、快速原型、医学等领域广泛应用的技术,是目前CAD/CAM研究领域的热点问题,而复杂曲面的重建是逆向工程研究的核心问题。逆向工程中广泛应用的重构方法是B样条曲线算法[1-2],B样条算法又可以分为B样条逼近曲线算法和B样条插值曲线算法。B样条逼近曲线算法,简单易操作,拟合曲线不通过控制顶点,一般通过增加控制点数和调整节点向量来提高拟合精度;B样条插值算法能使插值曲线通过所有的型值点,具有一定的实际意义,但其拟合过程需要求解方程组反算控制点的位置,要对数据点和节点向量做特殊的规定,计算过程较为复杂,也可以通过增加插值点数和调整节点向量来提高拟合精度。3次均匀B样条可以集逼近插值于一体且形状可调[3],但均匀B样条曲线在首末端点处的形状较难控制。
逆向工程通常要求使用尽可能少的控制点数量来实现高精度的曲线曲面重构。在压缩控制点方面,Piegl等[4]构造了具有非退化特性的参数区间,增加了节点选择的灵活性,使控制点数目明显减少;Park等[5-6]在二分法的基础上,提出一种基于误差自适应控制的逼近算法,可以得到满足给定误差阈值的控制点较少的逼近曲线;魏栋等[7]提出将离散点的曲率特征点作为初始逼近曲线,在误差较大处增加新的插值点,通过粒子群算法优化控制点的位置,进一步提高逼近精度;程仙国等[8]提出基于B样条曲线段复杂度节点配置算法,在保证相同逼近精度的条件下使用更少的控制点;张毓华等[9]提出基于几何信息均布的B样条曲线节点设置方法,在控制点数量相同的情况下实现较高精度的逼近;江本赤等[10]提出将曲率优势点作为轮廓约束点构造初始逼近曲线,在需要改善拟合精度的区域增加约束点,直到获得满足精度要求的B样条曲线。
通过合理的参数化方法可以提高B样条曲线的逼近精度,潘日晶[11]提出利用数据点的参数化和节点向量的自由度,构造在各数据点满足切向约束的二次B样条插值曲线,直观地控制插值曲线达到预期形状;于谦等[12]提出利用二次B样条本身的几何性质进行参数化,使曲线在每个插值点上都满足指定的切向,但节点矢量的计算和控制点的反算过程较为复杂。
本文结合B样条逼近曲线和B样条插值曲线的优点,提出一种插值于控制点的局部形状可调整的B样条逼近曲线算法。所提出的算法集逼近、插值于一体,且能够实现控制点处的切向特性和曲率特性的控制和调整;所提出的算法能使用更少的控制点数量和最简单的节点矢量设置实现对离散数据点的高精度逼近。
1 改进的3次准均匀B样条曲线算法
1.1 基本概念及性质
设控制点集D=di{xi,yi,i=0,1,2,…,n},B样条逼近曲线方程可写为[13]:
(1)
其中di为控制点,k为逼近曲线的次数,Ni,k(u)称为k次B样条基函数,它是由一个称为节点向量的非递减的参数u的序列U=(u0≤u1≤…≤un+k+1)所决定的k次分段多项式,其表达式为:
(2)
式中,Ni,k(u)的双下标中第二下标k表示曲线的次数,第一下标i表示控制点的序号。为了对曲线在端点的行为有较好的控制, 节点矢量的两端点取重复度k+1, 即u0=u1=…=uk=0,un+1=un+2=…=un+k+1=1。剩下的n-k个内节点(uk+1,uk+2,…,un)可根据不同的方法进行设置。
性质对3次均匀B样条来说,若节点ui处对应的控制顶点是di,则曲线在参数ui处的点用德布尔算法的递推公式可表示为:
(3)
所以,只要取合适控制顶点,B样条曲线可插值其部分控制顶点。另外,B样条曲线在c(ui)处的切线平行于向量di+1-di-1。
因为3次均匀B样条曲线在首末端点处的行为很难控制,而3次准均匀B样条曲线是最常用的,因此把上述的性质推广到3次准均匀B样条曲线中,并对得到的推论进行证明。
推论对于3次准均匀B样条逼近曲线,除首末端点外,三个顺序控制点共线且等间距分布时, 逼近曲线会通过中间的控制点,B样条曲线在c(ui)处的切线平行于向量di+1-di-1。
证明计算参数u∈[ui,ui+1],对应的B样条曲线上的值可用德布尔算法的递推公式表示为[13]:
(4)
式中,u∈[ui,ui+1]∈[uk,un+1]。
(5)
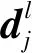
(6)
式中,j=i-k,i-k+1,…,i-l,l=1,2,…,k,对式(6)规定0/0=0。

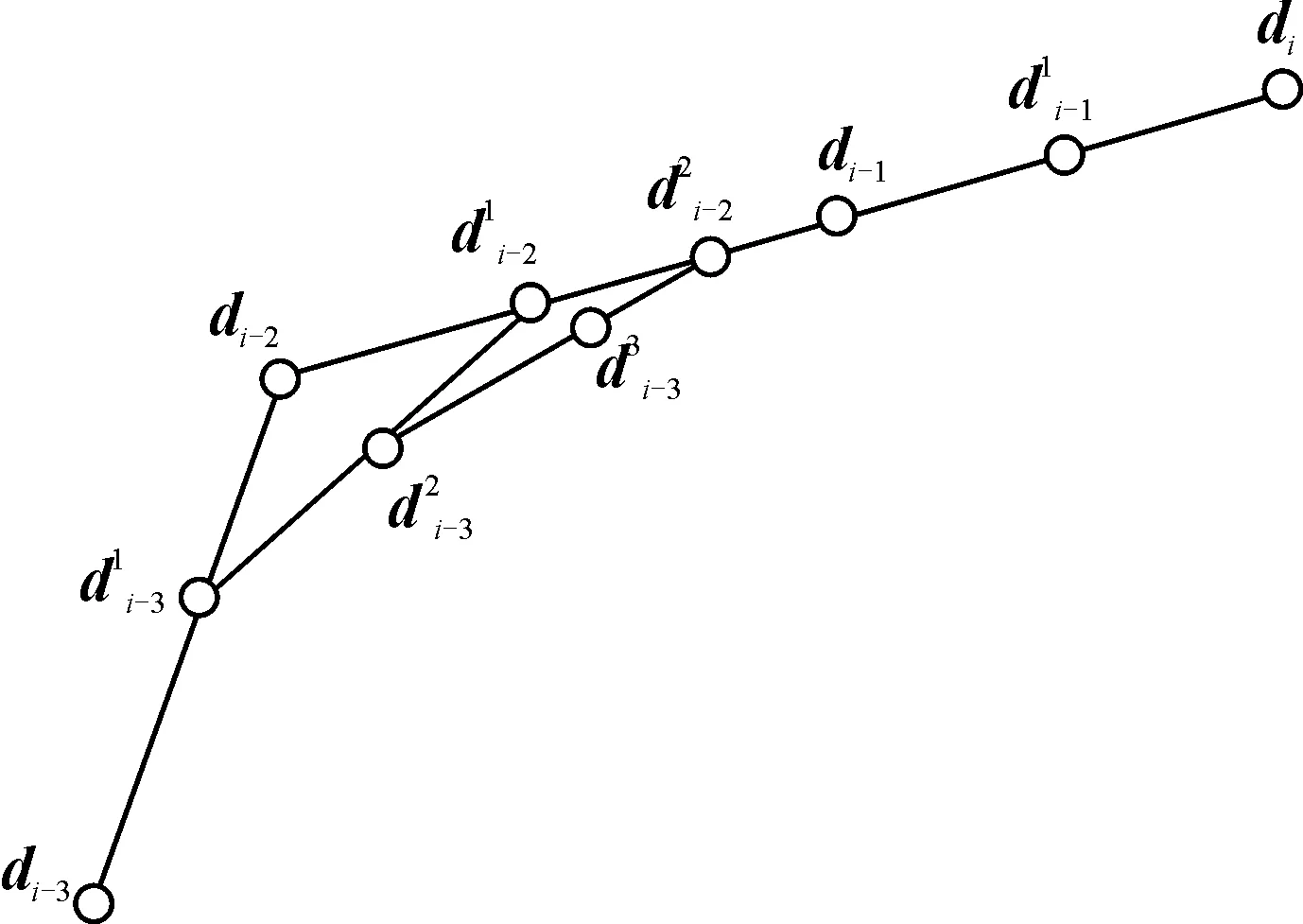
图1 3次准均匀B样条曲线上点c(u)的德布尔算法示意图Fig.1 Schematic diagram of the Debord algorithm for point c(u) on the 3rd quasi-uniform B-spline curve
要证明参数u对应的曲线上的一点c(u)位于控制点di-1处,则递推过程必需满足以下两个条件:
(7)
(8)

(9)
(10)
(11)
(12)
(13)
通过式(5)和(6)计算得到:
(14)
把式(14)代入(15)可得:
(15)
由于di-1是di和di-2的中点, 所以:
(16)
把式(16)代入式(15)即可得:
(17)
证明完毕。
参数u对应的曲线上的点是u∈[ui,ui+1]的曲线段c(u)的分段连接点c(ui+1), 且c(ui+1) 位于di、di-1和di-2所在的直线的中点,即di-1点。
1.2 本文算法的提出
基于上述结论,本文提出一种通过增加辅助控制点的方法,使B样条逼近曲线通过控制点,并引入形状参数S和L实现逼近曲线局部形状的动态调整。
图2 (a) 是4个控制点的3次准均匀B样条曲线,图2(b)是本文算法得到的插值于控制点的3次准均匀B样条曲线。图中d1、d2、d3和d4为控制点,d20、d21、d30和d31为控制点d2和d3的辅助控制点。从图2(b)中可以看出,引入辅助控制点后,逼近曲线通过对应的控制点。

图2 本文算法实现原理示意图Fig.2 Schematic diagram of the proposed algorithm implementation principle
1.3 方法的实现
1.3.1形状参数初始化
由于切向参数S和曲率参数L决定了辅助控制点的位置,从而决定了该处拟合曲线的形状,对拟合曲线的精度有决定性作用。根据大量仿真实验, 本文给出逆向工程中切向参数S和曲率参数L的初始化方法。
1) 在逆向工程中一般给出离散数据点集P=pq{xq,yq,q=0,1,2,…,h},h为离散数据点的总数。控制点处的切向参数S通过控制点所在位置的前后数据点计算,假设控制点di在离散数据点集中为点pq,则Si可表示为:
(18)
2) 参数Li为相邻控制点之间的距离乘以比例因子λi,可表示为:
(19)
式中,Li0表示位于该控制点前面的辅助控制点与控制点之间的距离;Li1则是位于该控制点后面的辅助控制点与控制点之间的距离;‖·‖表示两点之间的欧几里得距离。控制点集一经确定,相邻控制点之间的距离也确定,可以通过调整比例因子λi来调整辅助控制点的位置。
因为参数λi与该控制点处的曲率特性密切相关,为了降低初始逼近曲线的误差,本文给出Li初始化方法,如表1所示。

表1 λi与曲率的对应关系
Ki为控制点di在离散点列中通过U弦长[14]计算得到的曲率。当然,初始逼近曲线不可能完全达到精度要求,曲线在两个控制点之间的形状也受到切向参数Li的影响,对形状参数进行适当调整可大幅度提高逼近精度。
1.3.2辅助控制点位置
控制点列记为D=di{xi,yi,i=0,1,2,…,n},对于第i个控制点di(xi,yi),其前辅助控制点di0(xi0,yi0)的位置坐标可以通过联立几个方程来求解:
(20)
式中,Si为斜率参数, 在计算机辅助几何设计(CAGD)中可根据设计曲线在控制点di处的切向特性进行设置;Li为辅助控制点与对应的控制点之间的距离。对应的后面的辅助控制点di1(xi1,yi1)的坐标同理可求。
辅助控制点的位置由两个参数进行控制和调整:切向参数S和辅助控制点到对应的控制点之间的距离L,如图3所示。

图3 参数S和L对逼近曲线形状的影响Fig.3 Effect of parameters S and L on the shape of the approximation curve
参数S和L对于曲线形状具有不同的几何意义。切向参数S决定了逼近曲线在控制点处的切向特性,L则决定了曲线在控制点处的曲率特性,L越小,曲线越陡峭,L越大,曲线越平缓。
1.3.3节点向量
节点向量的确定需要根据控制点个数n和逼近曲线的次数k来确定。本文中增加的辅助控制点个数计入控制点数。如控制点集中有n个控制点, 除去首末端点外其余控制点各增加两个辅助控制点,增加的辅助控制点个数为2×(n-2),则增加后总的控制点数为:
m=3n-4
(21)
增加辅助控制点后的节点向量根据m和k进行设置,对于开曲线和首末端点仅位置连续的闭曲线,准均匀B样条的两端节点取重复度k+1,便于对曲线端点行为有较好的控制,内节点均匀分布,即u0=u1=…=uk=0,un+1=un+2=…=un+k+1=1。剩下的m-k个内节点均匀分布。
1.3.4逼近误差计算
B样条曲线的逼近误差指离散点列到逼近曲线的距离的最大值。本文提出一种逼近误差的计算方法,设离散点列P=pq{xq,yq,q=0,1,2,…,h},p(u)为参数u对应的逼近曲线上的点,pq点处的误差εq为:
εq=min‖pqp(u)‖
(22)
其中,参数u均匀取值,通过不断细化u的取值间距,得到较为准确的误差为止。误差的最大值、平均值和均方差可计算为:
(23)
式中,max表示取最大值;mean表示计算平均值;std表示计算均方差。
1.4 粒子群算法优化辅助控制点的位置
粒子群优化算法(Particle Swarm Optimization,PSO)的思想源于群鸟捕食行为。用数学模型模拟鸟群觅食的过程,每一个数学问题的解看作是一只鸟,称作“粒子”,所有的粒子都由一个适应度函数来判断当前位置的好坏,每一个粒子都有记忆功能,能够记住搜寻过的最佳位置,每个粒子还有一个速度来决定搜寻的距离和方向,这个速度可以根据它本身的飞行经验和同伴的飞行经验进行动态调整。
设有N个粒子在R维搜索空间搜寻,则第t个粒子的位置为[15]:
Xt=(xt1,xt2,…,xtR),t=1,2,…,N
(24)
第t个粒子经历过的最好位置:
pbest,t=(pt1,pt2,…,ptR)
所有粒子经历过的最好位置:
gbest=(p1,p2,…,pR)
粒子群的飞行速度更新公式为:
(25)
式中,vtr∈[-vmax,r,vmax,r]。
位置更新公式为:
xtre+1=xtre+vtre+1, (r=1,2,…,R)
(26)
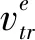
粒子群优化算法在本文中的应用说明:本文要求解的问题是寻找一组解Si和λi使得B样条逼近曲线的逼近误差最小。Si和λi的调整范围根据离散数据及控制点的特征进行设定。适应度函数为逼近误差的平均值,误差的计算方法参照1.3.4节内容。
优化辅助控制点位置的PSO算法的具体步骤为:
步骤1 初始化粒子,粒子的初始位置按照参数Si和λi的初始值计算得到;
步骤2 构造逼近曲线,计算初始适应度值,将粒子当前的适应度值ξi作为当前粒子的最优值pbest,i,并记住此时的参数Si和λi,然后选出总体最优值作为gbest;
步骤3 按照式(25)和(26)更新粒子的速度和位置,重新计算复制控制点的位置,构造逼近曲线,计算粒子的适应度值,若ξi 步骤4 若最优值gbest计算的适应度值小于设定的阈值或者迭代次数大于设定的最大迭代次数,则停止计算,输出pbest,i、Si、λi和gbest,绘制逼近曲线;否则转步骤3。 步骤1 提取控制点。对于给定的待拟合的离散数据点,提取曲率优势点作为控制点[12]。 步骤2 确定辅助控制点的初始位置。根据公式(18),计算辅助控制点所在直线的斜率Si;通过控制点所在离散点处的曲率值及表1,设定参数λi,结合式(20),确定辅助控制点的初始位置。 步骤3 节点向量。根据式(21)确定控制点的个数,两端节点取重复度k+1, 便于对曲线端点行为有较好的控制,内节点均匀分布。3次准均匀B样条,k=3。 步骤4 由式(1)和(2)绘制B样条曲线。 步骤5 根据式(22)和(23)计算拟合曲线的误差,判断误差是否满足要求,若满足,结束;若不满足,执行步骤6。 步骤6 对于误差大于规定阈值的控制点,使用1.4节描述的方法对该控制点对应的辅助控制点位置进行调整,调整后,执行本节步骤4(注:节点向量不用更新)。 B样条曲线广泛应用于曲线曲面重构技术中,通过增加控制点的个数来提高B样条曲线的拟合精度。控制点个数的增加会大大降低拟合的效率。在逆向工程中,待拟合的点基本都是曲线上或者曲面上的点,要求逼近曲线能最大程度通过待拟合的点以降低逼近误差。 如图4所示,以某叶片截面的离散数据为例进行分析。离散点数据为234个,分布范围约50 mm×25 mm。 图4 某叶片截面离散数据Fig.4 Discrete data of a blade section 应用本文算法对某叶片234个离散数据点进行曲线重构。首先,提取曲率特征点作为控制点,10个顺序控制点坐标为P0=[-20.5, 24; -12.644 5, 18.738 9; 2.815 0, 11.961 8; 13.704 1, 10.389 8; 21.101 1, 10.447 5; 15.786 2, 5.594 7; 3.412 7, 3.713 5; -9.062 0, 9.722 9; -19.182 6, 20.437 7; -20.5, 24];为了使闭曲线首末端点相连,控制点中首末端点取同一个点; 为了对端点处的曲线形状也能进行控制和调整, 在两端点处各增加一个内辅助控制点d11和d100; 根据最终的控制点数确定节点向量为NodeVector=[0, 0, 0, 0, 0.04, 0.08, 0.12, 0.16, 0.20, 0.24, 0.28, 0.32, 0.36, 0.40, 0.44, 0.48, 0.52, 0.56, 0.60, 0.64, 0.68, 0.72, 0.76, 0.80, 0.84, 0.88, 0.92, 0.96, 1, 1, 1, 1]。执行流程如1.5节所示。 图5(a)为初始拟合曲线,从图中可以看出,拟合曲线和数据点之间有较大的误差。图5(b)为对参数进行调整后的拟合曲线。表2为调整后的形状参数表。从图5(b)中可以看出,拟合曲线和数据点具有很好的贴合度,拟合曲线光顺。通过形状参数的调整,拟合曲线的平均误差从0.019 6 mm降低为0.007 5 mm,最大误差从0.561 5 mm降低为0.034 8 mm。 图5 本文算法拟合曲线Fig.5 Fitting curve using proposed algorithm 控制点Siλi0λi111.000.302-0.651.001.053-0.261.000.804-0.010.801.005-1.870.320.3560.500.901.007-0.160.800.908-0.751.001.009-1.501.000.30101.000.5 本文算法的逼近误差如表3所示,可以看出,本文使用10个控制点,通过形状参数对逼近曲线的局部调整,实现了对离散数据的高精度逼近,且逼近误差分布较为均匀。 表3 本文算法逼近误差 图6为曲率变化较大区域的放大图,从图中可以看出,本文算法对曲率变化较大的区域的曲线有较好的控制,相对于其他两种算法,使用的控制点数较少。 图6 局部放大图Fig.6 Enlarged view of regions I and II 应用传统的3次准均匀B样条逼近曲线算法进行曲线重构,使用与2.1节同样的曲率优势点作为初始控制点,通过逐个增加控制点的方法来提高逼近曲线的精度,直到平均误差小于0.05。 仿真结果如图7所示。图7(a)为初始逼近曲线,从图中可以看出,逼近曲线比较光顺,但逼近曲线与离散点之间有明显的偏差;图7(b)为控制点增加到68个时,平均误差小于0.05的最终逼近曲线,在曲率变化较大的地方控制点较多。 拟合曲线的误差如表4所示,从表中可以看出,随着控制点数的增加,逼近精度得到明显改善,最终的逼近曲线使用了68个控制点。 表4 逼近误差 B样条逼近曲线的优点在于算法简单,拟合曲线较为光顺,如图7所示,可以通过增加控制点提高拟合曲线精度。但即使将所有的点都作为控制点,控制点与拟合曲线之间存在的误差也无法消除,如图8所示。 图7 B样条逼近算法仿真结果Fig.7 Simulation results of B-spline approximation algorithm 图8 图7中III区域放大图Fig.8 Enlarged view of region III in Fig.7 根据文献[12]构造的二次B样条插值曲线算法对离散点列进行拟合,通过特殊的节点矢量设置,增加插值点处的切向约束,使曲线在每个插值点上都满足指定的切向。通过将误差最大处的离散点添加到控制点列来提高插值曲线的精度,直到平均误差小于0.05。 仿真结果如图9所示。从图中可以看出,图9(a)中逼近曲线与离散数据点之间有微小偏差;图9(b)逼近误差明显降低,同样在曲率变化较大的地方控制点较多。 表5为文献[12]方法的拟合误差,在拟合误差最大值小于0.05时,插值点数为39,最后的平均拟合误差较小。 对三种方法的控制点数量、初始逼近误差及最终逼近误差进行对比分析,结果如表6和表7所示。从表6中可以看出,在使用相同的控制点时,本文方法的初始最大逼近误差、平均误差和均方差远小于其他两种方法。从表7可以看出,本文方法使用最少的控制点数,实现了与其他两种方法相近的逼近精度。 表6 初始逼近曲线误差对比 表7 最终逼近曲线误差对比 图10为三种方法最终拟合误差分布图,从图中可以看出,在两段曲率变化平缓的区域,文献[12]的逼近精度最好,在中间曲率变化较快的位置,本文算法的误差得到了较好的控制,且在该区域使用的控制点数远小于其他两种算法。 图10 逼近误差分布Fig.10 Approximation error distribution 本文对逆向工程中的B样条曲线重构关键技术进行了研究,提出了一种集逼近、插值于一体的B样条曲线算法,且能够实现控制点处的切向特性和曲率特性的控制和调整。所提出的曲线重构方法大大压缩了曲线重构的控制点数量,且算法简单易操作,其主要结论为: 1) 使用本文方法,通过10个控制点确定的初始B样条曲线的逼近误差远小于传统的3次准均匀B样条逼近曲线算法和2次B样条插值算法; 2) 使用本文算法获得的最终逼近曲线可达到与其他两种方法同等的逼近误差,且使用的控制点数远少于其他两种方法; 3) 本文算法对曲率变化较大区域的逼近曲线误差有较好的控制。1.5 实现步骤
2 应用实例分析

2.1 本文方法


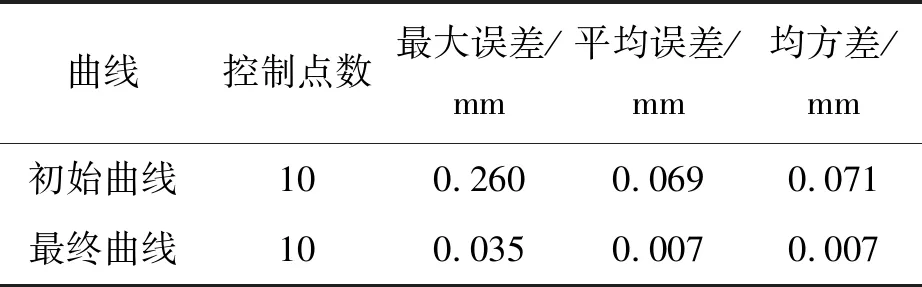

2.2 3次准均匀B样条逼近算法



2.3 B样条插值算法
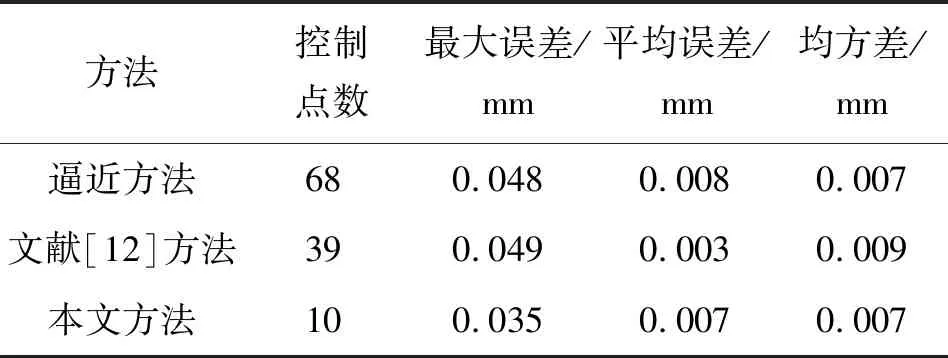
2.4 结果分析


3 结 论

