解一维空间分数阶对流扩散方程的二阶半隐式非对称迭代算法

朱 琳

(宁夏大学数学统计学院，宁夏银川750021)

分数阶偏微分方程可用于描述一些反常扩散现象，在物理、化学、水文地理学和经济学等诸多领域中应用广泛，近几十年来，其理论研究得到了蓬勃的发展．解分数阶偏微分方程的数值方法主要有有限元法［1－2］、谱方法［3－4］、DG 方法［5］和有限差分方法［6－12］等．

由于分数阶算子具有非局部记忆性，使得分数阶偏微分方程的求解比整数阶微分方程的求解需要花费更多的计算时间和更高的存储要求．文献［13－14］利用非对称迭代技术提出了一种半隐格式，既保留了隐格式稳定性好的优点，又不用求解线性代数方程组．本文拟采用这种非对称迭代技术，结合加权移位 Grünwald －Letnikov算子［15］和中心差分算子构造一个二阶半隐式有限差分格式，求解一维分数阶对流扩散方程．此格式形式上是隐式的，但是通过对奇数和偶数2个时间层分别选取不同的节点模板，从而可以进行显式计算，节约了计算时间和存储空间，这种思想在本文中将进行详细介绍．

一些学者采用非对称迭代技术构造了许多不同类型的并行算法，比如在文献［16－17］中，应用对称迭代技术解椭圆方程，仅给出了稳定性，且只提到截断误差是 O(Δth－1+Δt+h);在文献［18］中，只是在实际的计算中应用了非对称迭代技术．文献［19］得到了空间分数阶对流方程解析解和离散解在 l2范数意义下误差估计式为O(Δt2h－2(α－1)+Δt+h)．本文在此基础上给出了空间分数阶对流扩散方程的二阶半隐有限差分格式，用Fourier分析法证明了此格式的稳定性，给出了截断误差及解析解与离散解在l2范数意义下的误差估计O(Δt2h－2(α－1)+Δt+h2)，其中 Δt和 h 分别为时间和空间方向的步长．

1 非对称迭代格式

研究下列分数阶对流扩散方程:其中，α 是分数阶空间项导数，且 1＜α≤2，d(x，t)≥0，c(x，t)≥0．

做出以下记号:

其中，n=0，1，…，≤T/Δt，l=0，1，…，K．

Riemann－Liouville［20］分数阶导数定义为其中，n＞α＞n－1≥0(n为整数)，Γ 是伽马函数．

计算Riemann－Liouville导数的经典 Grünwald公式和移位 Grnüwald 公式［9－10］分别为:

其中，K 是正整数，gk是 Grünwald 系数，且

引理 1．1［21］当 1 ＜ α ≤ 2，(4)式定义的Grünwald系数{gk}时具有如下性质:g0=1，g1=－α ＜ 0，1 ≥ g2≥ g3≥ … ≥ 0，=0，≤0(m≥1)．

将(3)式中经典和移位Grünwald算子加权平均用来近似计算Riemann－Liouville分数阶导数得

将(5)式简化为

其中

由引理 1．1，经过简单推导，可得引理 1．2［15］．

用中心差分算子离散对流项得到

结合(6)和(7)式，分别采用向后或向前Euler公式离散时间导数得到方程(1)的2种隐式有限差分格式为:

或

接下来，结合非对称迭代技术对(8a)和(8b)式进行改造，设 1≤l≤K－1，n≤N=T/(2Δt)得到如下半隐式有限差分格式:

其中(9)式满足的初边值条件为:

下面介绍显式解方程组(11)的过程．

1)求解方程(11a)，即从时间层t2n计算到时间层t2n+1．从给定的边界值v20n+1开始，依次从左到右可以计算出 l=1，2，…，K－1的值 v2ln+1，在每次应用(11a)式时，v2l－n1+1已经知道，从而隐式格式进行了显式化的计算．

2)求解方程(11b)，即从时间层t2n+1计算到时间层t2n+2．从已知的边界v2Kn+2开始，依次从右向左可以计算出 l=K－1，K－2，…，1 的值 v2ln+2，计算也是显式的．

交替使用(11a)和(11b)式来进行计算，就实现了对隐格式(11)式的显式化计算，不用求解一个线性代数方程组．

2 差分格式的稳定性分析

用Fourier方法讨论非对称迭代格式(9)的稳定性．

其中，A=(Aij)(K－1)×(K－1)，B=(Bij)(K－1)×(K－1)，且 Aij、Bij定义如下:

一般地，假设 s=0，bR=0，则(12)式变形为:

令v2ln+1=Z2n+1eiβlh，其中 β 是非负整数，代入(15)式得:

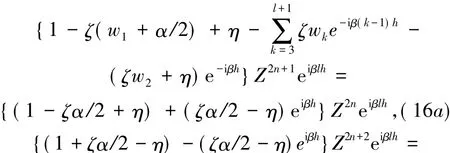
则由(16)式可得:Z2n+2=G2n+2Z2n，其中

有

引理 2．1 假设 s=0，bR=0，对于(12)式，若α∈，则

．由于

所以

根据引理1．1和引理1．2得:

故

如果 ζα/2＞η 成立，同理可得 G1≤1，则，从而得到了结论，证毕．

令

将(21)式代入(13)式可得:

经过简单推导，可得:

其中m、n是非负整数．

上式等价于下列方程:其中，1≤l≤K－1，n≤N=T/(2Δt)．

欲证明‖(I－A)(I+A)－1‖≤1，只需证明(24)式的增长因子的模小于1，这个证明方法和引理2．1中类似，这里不再赘述．同理可得‖(I+B)－1‖≤1，证毕．

定理2．3 对已经得到的满足初边值条件(10)式的非对称迭代格式(9)式，假设 c(x，t)=c，d(x，t)=d是常函数且bR=0，则当α∈时，是一致稳定的，且成立，其中m、n是正整数．

证明 由引理2．1、引理2．2 和(23)式，可得综合(21)、(25)和(26)式，可得反复运用(27)式可得结论，证毕．

3 差分格式的误差分析

本节讨论非对称迭代格式(9)的误差估计．首先假设 c(x，t)=c，d(x，t)=d 是常函数．

设umi=u(xi，tm)是满足方程组(1)的真实解，则有:

利用泰勒展开公式，可得:

由于 1＜α＜2，将(29)式代入(28)式得 t2n+1时刻的截断误差:

同理，可得t2n+2时刻的截断误差为:

设 Um=(u1m，um2，…，umK－1)，下面给出方程组(1)的精确解和计算解的误差估计．

定理 3．1 设u(xi，tn)是方程组(1)的精确解，vn是其计算解，如果 c(x，t)=c，d(x，t)=d 都是常函数，且空间步长h和时间步长Δt都足够小时，存在与h和 Δt均无关的正常数 C且 m≤T/Δt，使得‖Vm－Um‖≤C(Δt2h－2(α－1)+Δt+h2)．

注1 由(29)式可知，本文给出的半隐有限差分格式(9)的局部截断误差为而定理4．1给出的其精确解与解析解的误差估计是应用了非对称迭代格式后具有的特点，该定理证明过程繁琐且与文献［19］中相关定理证明类似，此处略去．

4 数值算例

例1 考虑如下的空间分数阶对流－扩散方程

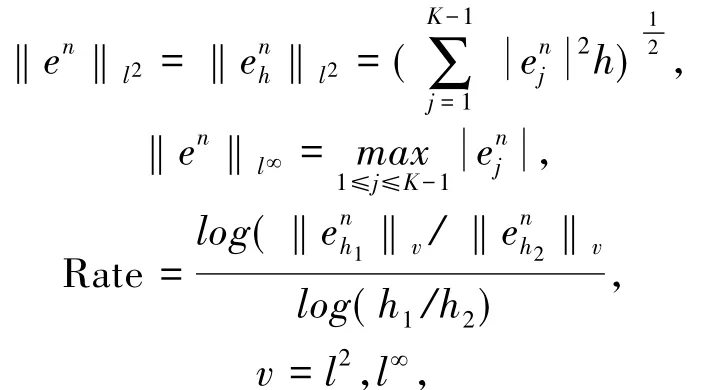
其中h1、h2是空间步长．

由定理4．1可知，方程组(1)的精确解和计算值之间的误差估计为 O(Δt2h－2(α－1)+Δt+h2)．为了验证这个结果，则:

1) 取 Δt=Chα，此时收敛阶应为O(hα);

2)取Δt=Ch2，此时收敛阶应为O(h2)．对应不同的α选取不同的C从而更好的验证结果，其中C是非负整数．

表1～4分别给出了在t=1．0时刻的离散L2误差和离散L!误差，以及空间方向对应的收敛阶．分数阶导数 α 分别取1．6和1．8．显然，给出的对称迭代格式(9)在空间方向达到了理论分析的精度，甚至更高．

表1 例1在t=1时刻的误差和收敛阶Tab．1 Error and convergence rates for example 1

表3 例1在t=1时刻的误差和收敛阶Tab．3 Error and convergence rates for example 1

表4 例1在t=1时刻的误差和收敛阶Tab．4 Error and convergence rates for example 1

5 结束语

本文结合非对称迭代技术给出了一个半隐式的有限差分格式，形式上是隐格式，但是通过偶数和奇数时间层选取不同的节点模板进行显式化计算，并且通过分析，空间方向精确解和计算解的误差估计为 O(Δt2h－2(α－1)+Δt+h2)，通过选取合适的时间步长，收敛阶在l2范数意义下可以达到二阶，甚至更高．