RSA变型方案小解密指数攻击的改进分析*
孙哲蕾,彭力强,胡 磊,王 强
1.北京空间飞行器总体设计部,北京100094
2.中国科学院信息工程研究所信息安全国家重点实验室,北京100093
3.中国科学院数据与通信保护研究教育中心,北京100093
4.国家新闻出版广电总局 广播科学研究院,北京100866
1 引言
利用大整数因子分解问题的困难性,Rivest、Shamir和Adleman[1]在1978年提出了著名的RSA公钥加密体制.自提出以来,RSA 方案得到了广泛的应用和研究,它有效地解决了信息安全中数字签名、密钥共享等问题,是保障实际网络中密钥管理以及数字签名应用最为广泛的的公钥算法之一.为了方便后面描述,我们首先回顾标准RSA 方案的密钥生成过程.
RSA 的密钥生成算法:随机生成两个不同的且比特长度相同的素数p和q,N=pq为RSA 的模数.随机选取满足gcd(e,ϕ(N))=1 的正整数e,其中ϕ(N)=(p−1)(q−1),并通过扩展欧几里得算法计算得到d,使得ed=1(modϕ(N)).RSA 公钥加密方案的公钥为(N,e),私钥为(p,q,d).
除了标准RSA 方案外,结合效率和安全等因素考虑,研究学者还设计了若干RSA 方案的变型方案,例如基于中国剩余定理的快速解密标准CRT-RSA 方案[2]、Prime Power RSA 方案[3]等.由于RSA 方案及其变型方案的广泛应用,因此,关于它们的安全性也一直是密码学中的重要研究方向.
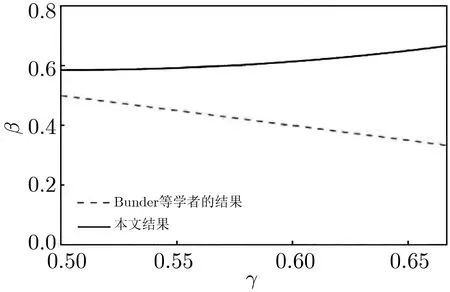
RSA方案的小解密指数攻击:1990年,Wiener[4]利用连分式方法,提出了在d 1995年,Kuwakado 等人[13]提出了一种基于奇异三次曲线y2≡x3+bx2(modN)的RSA 型方案,其中N=pq为模数.与标准RSA 方案不同的是,Kuwakado-Koyama-Tsuruoka 方案中的公钥e和私钥d满足ed=1(mod(p2−1)(q2−1)).2002年,Elkamchouchi 等人[14]将RSA 方案扩展到高斯整数环,与Kuwakado-Koyama-Tsuruoka 方案类似,公钥e和私钥d也满足ed=1(mod(p2−1)(q2−1)).类似地,Castagnos[15]在2007年提出了一种基于RSA 模数的概率方案,该方案中同样包括了与上述两方案[13,14]同样的模方程.因此,如何从模方程ed=1(mod(p2−1)(q2−1))中恢复出未知变量d,p,q是值得关注的问题. 2016年,Bunder 等人[16]利用连分式方法提出了关于上述三种方案的小解密指数d的恢复攻击,结果如下. 定理1令(N,e)为Kuwakado-Koyama-Tsuruoka 方案、高斯整数RSA 方案,或是Castagnos 方案的公钥,其中N=pq以及q 则模数N可以在多项式时间内被分解. 通过考虑素数p和q的规模,Bunder 等学者[17]进一步细化了定理1 的结果,并给出了一般情况下,即q 定理2令(N,e)为Kuwakado-Koyama-Tsuruoka 方案、高斯整数RSA 方案,或是Castagnos 方案的公钥,其中N=pq以及q 则模数N可以在多项式时间内被分解. 对于上述定理,若考虑一般情况下的加密指数e,即e的规模与N2一样.并且假设d与Nβ有相同的比特长度,其中0 <β< 2.令p与Nγ的比特长度一样,则q≃N1−γ,有µ≃N2γ−1.忽略与N无关的小系数,定理2 的结果可以描述为 即 在本文中,我们首先通过关系式ed=1(mod(p2−1)(q2−1)),即ed=1+k(p2−1)(q2−1)构造模方程, 其中,k为未知的正整数.之后,我们利用Coppersmith 方法求解上述模方程的一组根(k,−p2,−q2).具体地说,在应用基于格基算法实现的Coppersmith时,我们选取了若干多项式来构造格基矩阵,并且通过参数的设置,将未知变量的大小考虑在多项式的选取优化中.最终,我们将之前的结果β<1−γ提高到 为了更直观地比较我们得到的结果与文献[17]的结果,我们在图1中描绘了这两个式子所代表的区域,分别表示我们的方法与之前方法可以攻击的可行参数区域.图中虚线与横坐标所围成的区域代表文献[17]的结果,实线与横坐标所围成的区域代表我们得到的结果.通过对比可以看出,我们的方法大幅度改进了先前的安全性分析结果. 图1 Kuwakado-Koyama-Tsuruoka 等RSA 变型方案的小解密指数安全性分析结果对比Figure 1 Analysis of small decryption exponent on several RSA variant schemes 注意到,在2016年,Peng 等学者[18]利用Coppersmith 方法改进了定理1的结果,即p和q的大小满足与之前文献[18]内容不同的是,本文考虑一般情况下,即p和q的规模是任意的.我们在多项式的选取中,充分利用p和q的大小关系,即γ的大小,尽可能多地选取有帮助的多项式,从而达到最优的结果. 在本节中,我们简要介绍下基于格基约化算法Coppersmith 方法的原理,以及格的一些相关概念. 令h(x1,··· ,xr)=0(modW)为一个模方程,其中X1,··· ,Xr为该模方程要求解的根的绝对值的上界.相较于W,如果的值足够小,那么我们可以利用基于格的Coppersmith 方法在多项式时间内求解出所有的根该方法是由Coppersmith[19,20]在1996年首次提出的,它可以在多项式时间内求解模数分解未知的单变量模方程小根以及双变量整方程小根.之后,Howgrave-Graham[21]以及Coron[22]分别重新描述了Coppersmith 的工作[19,20],使得Coppersmith 方法便于理解及应用.2006年,Jochemsz和May[23]进一步给出了求解任意形式的多变量模方程或是整方程的一般性方法,使得Coppersmith 方法成为了研究公钥密码体制安全性的重要工具,尤其是关于RSA 方案及其变型方案安全性的研究. 本节简要回顾Coppersmith 方法.首先,我们介绍Coppersmith 方法中所用到的Howgrave-Graham[21]引理. 引理1(Howgrave-Graham[21])给定多变量方程Z[x1,··· ,xk],并且g(x1,··· ,xk)中至多有n个单项式.若如下两个条件同时成立 由如上引理可以看出,一旦上述条件满足,我们就可以将一个模方程的根转化为一个方程在整数上的根,并通过求解方程在整数上的根来恢复模方程的根.详细地说,为了求解k元的模方程h(x1,··· ,xk)=0(modp)的一组根我们需要找到k个多项式其中也是这些模方程的根,并且这些模方程系数的范式足够小,使得Howgrave-Graham 引理的条件成立,从而将求解这些模方程的小根转化为求解方程在整数上的根. 为了找到具有小范式的多项式,我们利用格以及L3格基约化算法.给定m个线性无关的向量由{w1,··· ,wm} 张成,是{w1,··· ,wm} 的所有整系数线性组合的集合,即 这里,我们称w1,··· ,wm为格L的一组格基.另外,如果我们定义由w1,··· ,wm为行的矩阵为W∈Rm×n,格的定义也可以写成是由矩阵W生成的格,记为 当m=n时,L(W)称为满秩格,这也是较为常用的格.格的行列式定义为如果格为满秩格,即W为方阵,我们有det(L(W))=|det(W)|.在本文中我们所构造的格均为满秩格,并且我们所构造的格为三角矩阵,因此我们可以简单地通过计算所有对角线上项的乘积得到格的行列式. 格已经被广泛应用到密码学的研究中,如何求解格的非零短向量是其中的关键问题之一.L3格基约化算法是由A.K.Lenstra、H.W.Lenstra 以及L.Lovász[24]在1982年提出的,它可以在多项式时间内解决指数因子的寻找近似最短向量问题, 引理2(L3[24])格L是一个维度为n的格.对格L应用L3格基约化算法,输出的约化基向量v1,··· ,vn满足 算法的运行时间为关于n以及格L的格基向量中向量长度最大值的多项式时间. 现在,我们可以根据上述两个引理来解释Coppersmith 方法是如何求解模方程h(x1,··· ,xk)=0(modp)的根首先,构造n个多项式h1(x1,··· ,xk),··· ,hn(x1,··· ,xk),并且这些多项式在模pm下的根都为其中m为自己选定的正整数.接下来,构造格L,其格基矩阵的行向量为所有多项式h1(x1X1,··· ,xkXk),··· ,hn(x1X1,··· ,xkXk)的系数向量.由于格L中的所有向量均可以表示为格基向量的整系数线性组合,因此为格中的任一向量所代表的多项式在模pm下的根.对格L应用L3格基约化算法,可以得到k个L3约化基向量,对应的多项式为一旦不等式det(L)1/n 注意到,在Coppersmith 方法中,只有L3格基约化算法所输出的向量对应的多项式相互之间代数独立,我们才能够通过计算结式或是Gröbner 基求解方程根.在本文中,如同之前的关于Coppersmith 方法的工作一样[7–12],我们假设这些多项式之间是代数独立的,并且我们通过实验结果验证了我们的分析. 在本节中,我们分析Kuwakado-Koyama-Tsuruoka 等三种RSA 变形方案的小解密指数的安全性.我们首先考虑的情况. 由ed=1(mod(p2−1)(q2−1)),我们得到如下方程, 其中,k∈N.问题转化为求解如下模方程的根(k,−p2,−q2).下面,我们估计根的大小.因为N=pq,且d与Nβ有相同的比特长度,e与N2的规模相同,其中0 <β< 2.令p与Nγ的比特长度一样,则q≃N1−γ.进一步,此时我们有 令X(:=Nβ),Y(:=N2γ)和Z(:=N2(1−γ))分别为根(k,−p2,−q2)的上界.注意到,未知变量之间存在代数关系yz=N2. 为了求解f(x,y,z)=0 mode,我们利用Takayasu-Kunihiro[25]的格构造方法,尽可能多地选取有帮助多项式,增大可求解根的范围.所选取多项式如下: 其中,m为正整数.对于任意的非负整数u,i,v,k1以及k2,(x,y,z)=(k,−p2,−q2)为所有选取多项式在模em下的根. 我们定义如下的坐标集合: 为了尽可能多地只选取有帮助多项式构造格,我们利用拆开的线性化技术[6],以及 Takayasu-Kunihiro[26]的转化方法,格基矩阵可以转化为三角矩阵,并且对角线上的元素为 由此可以看出,我们通过坐标集合Ix,Iy以及Iz所选取的多项式均是有帮助多项式.另外,在本节中我们考虑γ值较小,即的情况,否则集合Iy为空集.因此,我们可以通过计算对角线上元素的乘积得到格的行列式其中, 另一方面,格L的维数为 根据引理1与引理2,并且忽略m的小项o(m3),若满足det(L)1/n 综上所述,我们可以得到如下结论, 定理3令(N,e)为Kuwakado-Koyama-Tsuruoka 方案、高斯整数RSA 方案,或是Castagnos 方案中的公钥,其中N=pq以及ed≡1(mod(p2−1)(q2−1)).假设e,d分别与N2和Nβ有相同的比特长度,其中0<β<2.令p与Nγ的比特长度一样,其中则q≃N1−γ,若满足 则模数N可以在多项式时间内被分解. 在本小节,我们考虑任意情况下的e.首先,回顾Bunder 等学者[17]的结果.若公钥e<(p2−1)(q2−1)满足 则模数N可以在多项式时间内被分解.此时,不妨设e≃Nα,d≃Nβ.进一步,Bunder 等学者的结果可以描述为 我们注意到,Bunder 等学者的结果并不严谨,需要添加限制条件.因为,ed=1(mod(p2−1)(q2−1)),即α+β>2.这意味着因此,Bunder 等学者的结果应为 对于Coppersmith 方法,我们需要修改坐标集合为. 通过类似的计算,我们可以得到如下结论, 推论1令(N,e)为Kuwakado-Koyama-Tsuruoka 方案、高斯整数RSA 方案,或是Castagnos 方案中的公钥,其中N=pq以及ed≡1(mod(p2−1)(q2−1)).假设e,d分别与Nα和Nβ有相同的比特长度,其中0<β<2.令p与Nγ的比特长度一样,其中则若满足 则模数N可以在多项式时间内被分解. 我们利用数学软件Magma 2.11[28]实现了我们的分析,实验环境为Windows 10 操作系统,2.50 GHz Intel(R)Core i7-6500 处理器,8 GB 内存.表1记录了p在取不同规模大小情况下的实验结果,其中我们选的模数N的长度为1000 比特. 表1 实验结果Table 1 Experimental results 在本文中,我们利用Coppersmith 方法改进了Bunder 等人的分析结果,扩大了三种变型RSA 方案小解密指数攻击的参数范围.对于模方程ed≡1 mod(p2−1)(q2−1)中的未知变量的求解,我们在构造格时,通过添加额外的参数使得p和q在不同规模下,尽可能优化格的构造,提升了之前结果.1.1 背景知识


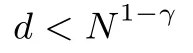

1.2 我们的结果
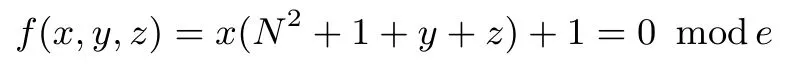

2 预备知识
2.1 Coppersmith 方法
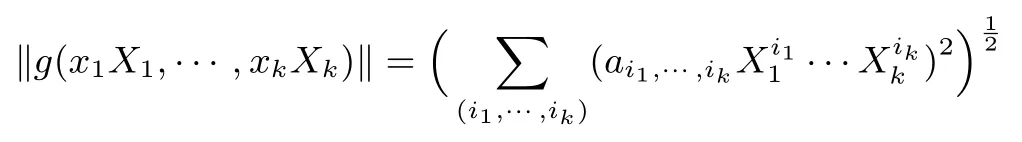

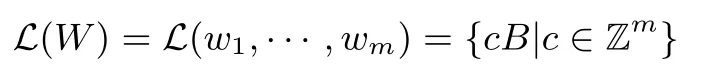

3 我们的分析结果
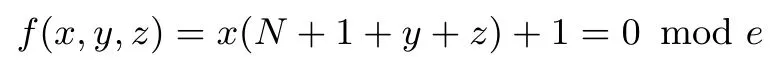
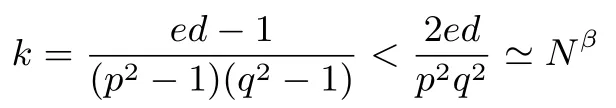



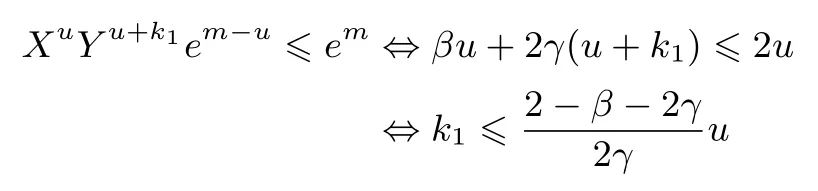


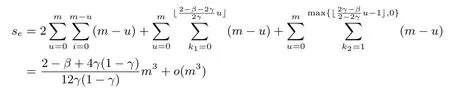
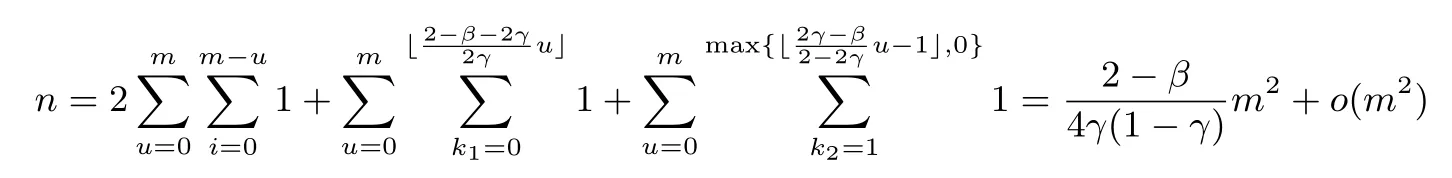

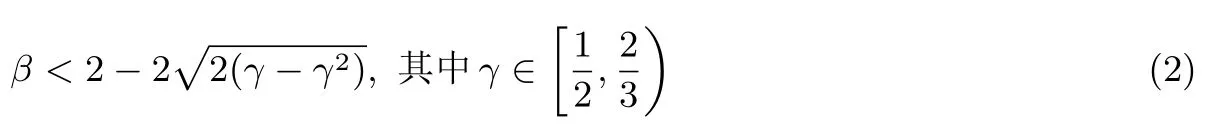
3.2 考虑任意e 的情况
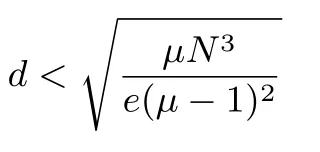
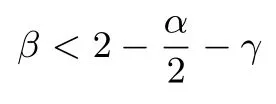
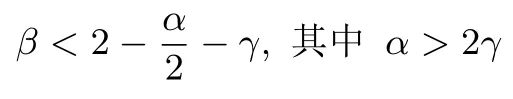

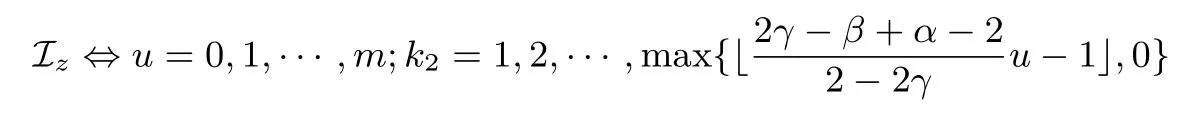
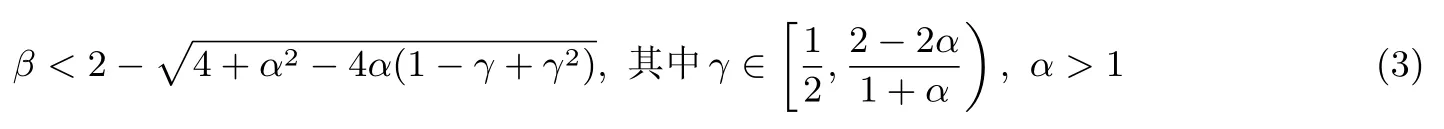
3.3 实验结果

4 总结

