基于高阶剪切变形理论的磁电弹性梁的非线性静力分析

许亮亮 郑玉芳 陈昌萍

摘 要：基于高阶剪切变形理论和Von Karman非线性理论建立磁电弹性梁的非线性模型，采用Hamilton原理推导磁电弹性梁的非线性平衡微分方程，利用伽辽金方法对该非线性偏微分方程组进行求解。数值计算中，具体讨论了外部荷载、跨高比、磁场及电场等因素对磁电弹性梁非线性静力响应的影响。

关键词：Reddy三阶剪切理论;Von Karman非线性理论;磁电弹性梁;伽辽金法

中图分类号：O343.5

文献标识码： A

随着科学技术的快速发展，智能材料的耦合性能引起学者们的关注。磁电弹性材料由于存在压电、压磁和磁电三种耦合效应，能够实现机械能-电能-磁能之间的能量转换，从而在智能结构和电子信息等领域得到广泛应用。再者梁构件广泛应用于工程实际，所以对磁电弹性梁力学行为的研究具有十分重要的意义。

江爱民等[1-4]根据横观各向同性磁电弹性体的三维基本方程，研究了在均布荷载作用下、集中荷载以及线性电势和磁势作用下，不同边界条件的磁电弹性梁的平面问题。Milazzo等[5]提出了一种可以等效磁电弹性层合梁的弹性单层梁的有限元模型，研究了磁电弹性层合梁的静力问题。Huang等[6-7]利用解析法和半解析法研究了在任意荷载作用下的各向异性磁电弹性梁的平面应力问题。Annigeri等[8]采用有限元方法研究了多相层状磁电弹性梁的自由振动问题。Vinyas等[9]采用总势能原理对热环境下的多层磁电弹性梁进行了静力分析。Xu等[10]基于欧拉-伯努利梁模型，研究了磁电弹性梁的屈曲和振动问题。Ansari等[11]在一阶剪切变形梁理论的基础上，建立了尺寸相关的非线性磁电弹性纳米梁模型，研究了具有不同边界条件的磁电热弹性纳米材料梁的后屈曲行为。Xiao等[12]基于Eringen的非局部弹性理论，分析了磁电热弹性纳米梁的非线性屈曲问题。Alibeigi等[13]利用Von Karman几何非线性等理论研究了不同热载荷、电场和磁场作用下磁电弹性纳米梁的屈曲响应。从研究成果来看，磁电弹性材料结构的非线性特性由于其复杂性，研究成果相对较少。

本文基于高阶剪切变形理论和Von Karman非线性理论建立磁电弹性梁的非线性力学模型，采用Hamilton变分原理推导了磁电弹性梁的非线性平衡微分方程。通过伽辽金方法对该非线性偏微分方程组进行求解，讨论外部荷载、梁的跨高比、磁场以及电场等因素对梁非线性静力响应的影响，探讨了磁电弹性梁的力-电-磁耦合机理。

1 基本方程

考虑长度为l，宽为b，高为h的矩形截面磁电弹性材料梁。Oxy 平面位于梁的中性层上，其原点位于最左侧的截面形心上。采用Reddy三阶剪切理论，梁的位移场可表示为：

u（x，z）=u0（x）+zφ（x）-cz3（φ（x）+dw0（x）dx），

w（x，z）=w0（x）。

（1）

其中，u0为中性层内任一点的轴向位移;w0为

纵向位移;φ为横截面转角，c=4/（3h2）。根据Von Karman几何非线性理论，可得到位移-应变关系如下：

εx=ux+12wx2， γxz=uz+wx。

（2）

将式（1）代入式（2），得到梁的应变为：

εx（x，z）=ε0x+zε1x-cz3ε2x，γxz（x，z）=γ0xz-3cz2γ1xz。

（3）

其中

ε0x=du0dx+12dw0dx2， ε1x=dφdx， ε2x=dφdx+d2w0dx2，γ0xz=φ+dw0dx， γ1xz=φ+dw0dx。

（4）

磁电弹性材料的本构关系如下：

σxx=C11εx+e31z+q31z，σxz=C55γxz，

（5）

Dz=e31εx-η33z-d33z，

（6）

Bz=q31εx-d33z-u33z。

（7）

其中，Cij、eij、qij、ηij、dij、uij分别是弹性常数、压电常数 、压磁常数、介电常数、电磁常数和磁导常数;σxx（σxz）、Dz和Bz分别为应力分量 、电位移分量和磁通密度分量;和ψ分别表示电势和磁势。

根据Hamilton原理

0=  ∫h/2-h/2∫（k）Ω

σxxδε（k）xx+σxzδε（k）xz-

Dzδz-Bzδz

dxdydz-

∫Ωqδwdxdy，

（8）

得到

0=∫h/2-h/2∫（k）Ω  N1δε（0）x+M1δε（1）x+

P1δε（2）x+Q1δγ（0）xz+K1δγ（1）xz-Dzδz-

Bzδzdxdydz-  ∫Ωqδwdxdy。

（9）

其中，q為横向荷载，N1，M1，P1，Q1，K1表示如下：

（N1，M1，P1）=∫h/2-h/2σxx（1，z，-cz3）dz，

（10）

（Q1，K1）=∫h/2-h/2σxz（1，-3cz2）dz。

（11）

将式（9）中δu0，δw0，δφ，δ，δψ分离出来，得到以下控制方程：

N1x=0，

（12）

x（N1dw0dx）-2P1x2+Q1x+K1x+q=0，

（13）

M1x+P1x-Q1-K1=0，

（14）

Dzz=0，

（15）

Bzz=0。

（16）

将式（6）～（7）中的Dz和Bz分别代入式（15）～（16），并考虑梁的上下表面磁场和电场的边界条件如下：

ψ=0，=0（z=-h/2），ψ=Ω0，=V0（z=h/2）。（17）

得到：

ψ，z=13λ1A1+λ3A3z3+λ1A2+λ3A4z+Ω0h，，z=13λ1A3+λ2A1z3+λ1A4+λ2A2z+V0h。

（18）

其中：

λ1=d33d233-η33μ33，λ2=-μ33d233-η33μ33，

λ3=-η33d233-η33μ33，A1=-3ce31dφdx+d2w0dx2，

A2=e31dφdx，A3=-3cq31dφdx+d2w0dx2，

A4=q31dφdx。

将式（3）～（5）代入式（10）和（11），得到

N1=du0dxA11+（dw0dx）2A12+T1，

M1=dφdxA21+d2w0dx2A22+T2，

P1=dφdxA31+d2w0dx2A32+T3，

Q1=φA41+dw0dxA42，

K1=φA51+dw0dxA52。

其中：

A11=∫h/2-h/2C11dz，

A12=∫h/2-h/212C11dz，

T1=∫h/2-h/2e31z+q31zdz;

A21=∫h/2-h/2z2C11-C11cz4dz，

A22=∫h/2-h/2-C11cz4dz，

T2=∫h/2-h/2e31z+q31zzdz;

A31=∫h/2-h/2-z4cC11+c2z6C11dz，

A32=∫h/2-h/2C11c2z6dz，

T3=∫h/2-h/2-cz3e31z+q31zdz;

A41=∫h/2-h/2C55-3cz2C55dz，

A42=∫h/2-h/2C55-3cz2C55dz;

A51=∫h/2-h/2-3cz2C55+9c2z4C55dz，

A52=∫h/2-h/2-3cz2C55+9c2z4C55dz。

将N1，M1，P1，Q1，K1代入控制方程式（12）～（14），并引入如下的无量纲化参数：

ξ=xl，δ=lh，u-0=u0l，w-0=w0h，A-1j=A1jC11h，

A-2j=A2jC11h3，A-3j=A3jC11h3，A-4j=A4jC11h，A-5j=A5jC11h，

T-1=T1C11h，Q=qC11，Ω=Ω0q31hC11，V=V0e31hC11。

则得到磁电弹性梁的非线性平衡微分方程为

d2u-0dξ2δ2A-11+dw-0dξd2w-0dξ22A-12=0，

（19）

d2u-0dξ2dw-0dξδ2A-11+dw-0dξ2d2w-0dξ23A-12+

du-0dξd2w-0dξ2δ2A-11-d3φdξ3δA-31-d4w-0dξ4A-32+

d2w-0dξ2δ2（A-42+

A-52+T-1）+dφdξδ3（A-41+A-51）+Qδ4=0，

（20）

d2φdξ2δ（A-21+A-31）+d3w-0dξ3（A-22+A-32）-dw-0dξδ2（A-42+A-52）-φδ3（A-41+A-51）=0。

（21）

2 数值求解

考虑磁电弹性梁为两端简支，则其边界条件可表示为：

ξ=0，1∶u-0=w-0=0，Mξ=0。

（22）

对应的位移解可取为：

u-0=∑SymboleB@

m=1sin（2πmξ）U，

w-0=∑SymboleB@

m=1，3，…sin（πmξ）W，

φ=∑SymboleB@

m=1，3，…cos（πmξ）Φ。

（23）

将式（23）代入控制方程式（19）～（21），应用伽辽金方法并取一阶截断对方程组进行处理之后可得到一组非线性代数方程组，对此方程组求解可求得相应的位移解。

3 数值结果与讨论

在数值计算中，选取材料由BaTiQ3和CoFe2O4组成，各组分体积分数为50%，其材料参数如下：

C11=C22=213×109 N/m2，

C12=113×109 N/m2，C55=50×109 N/m2，

C44=C66=49.9×109 N/m2，

e31=e32=-2.71 C/m2，q31=q32=222 N/Am2，

u33=0.839×10-4 Ns2/C2，

η33=6.37×10-9 C2/Nm2，

d33=2750×10-12 Ns/VC。

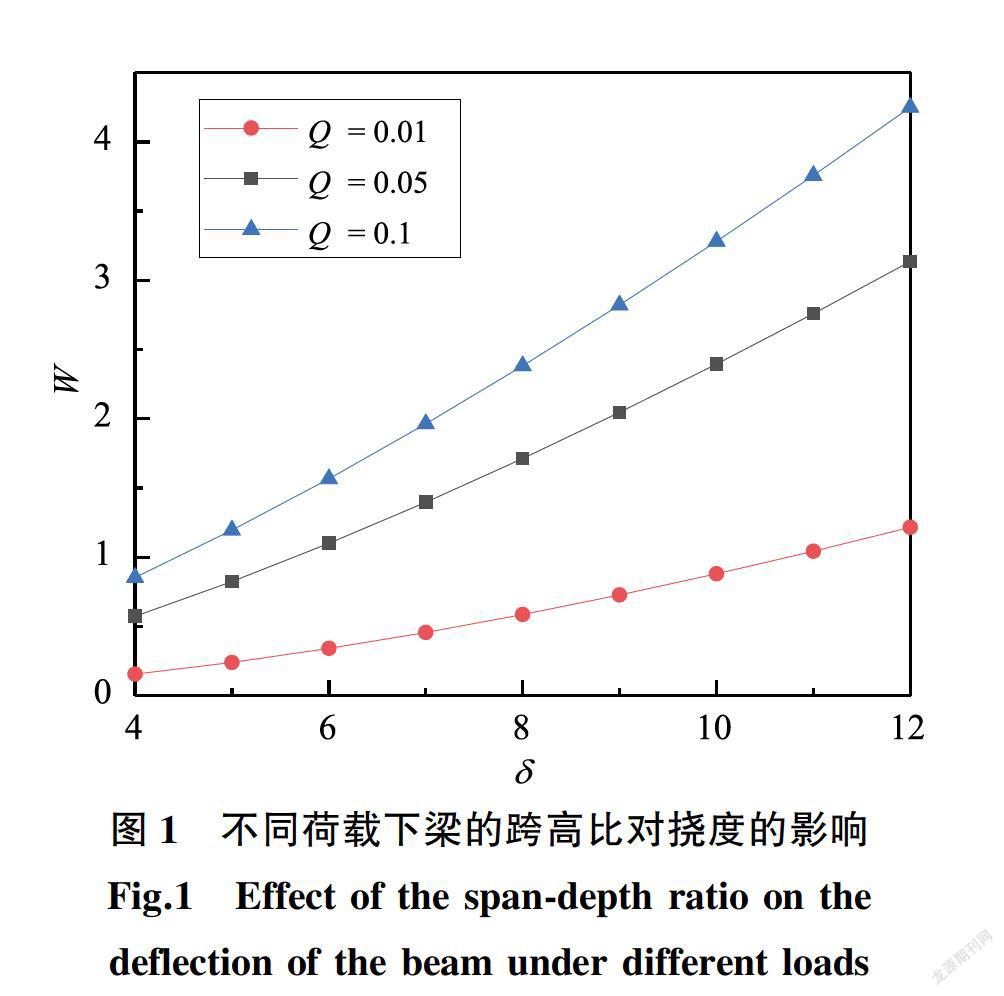
圖1给出了在h=0.5，Ω=0.001和V=0.001的情形下，梁跨中挠度在不同的外荷载下随跨高比的变化规律。从图中可以看出，加大外荷载或跨高比，都会使梁的挠度加大，且外荷载越大，梁变形的程度越大，体现了明显的非线性特征。

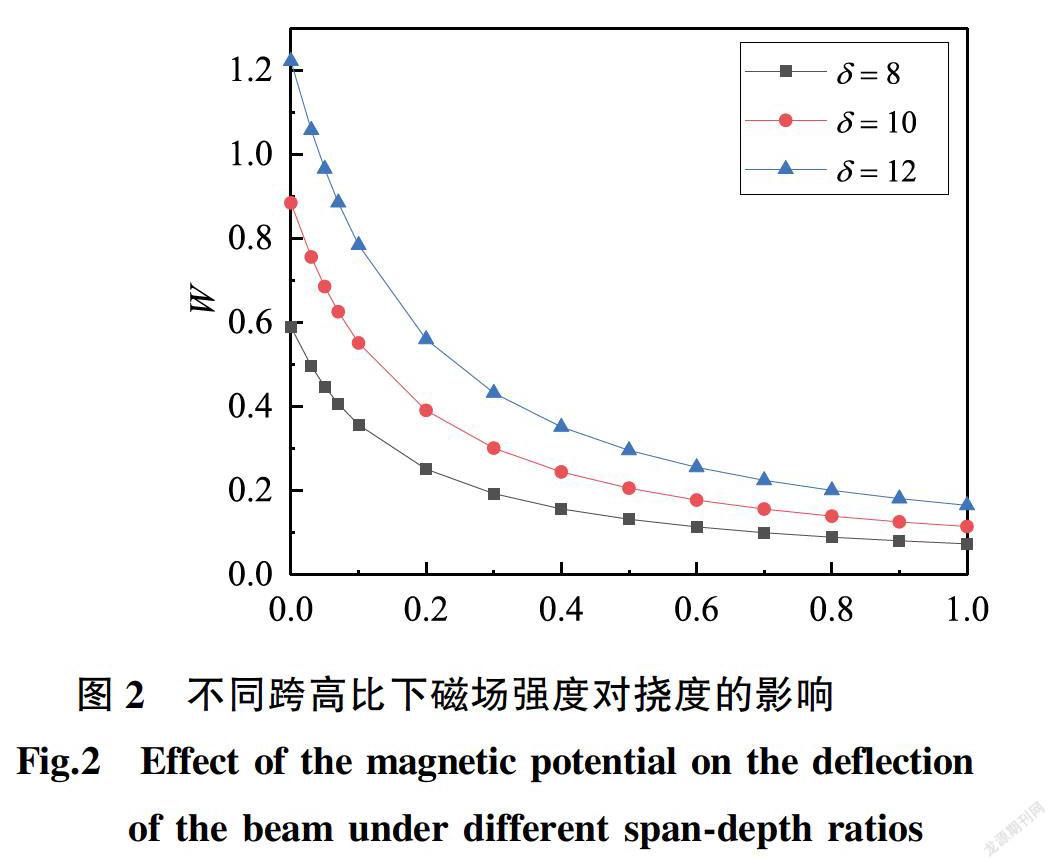
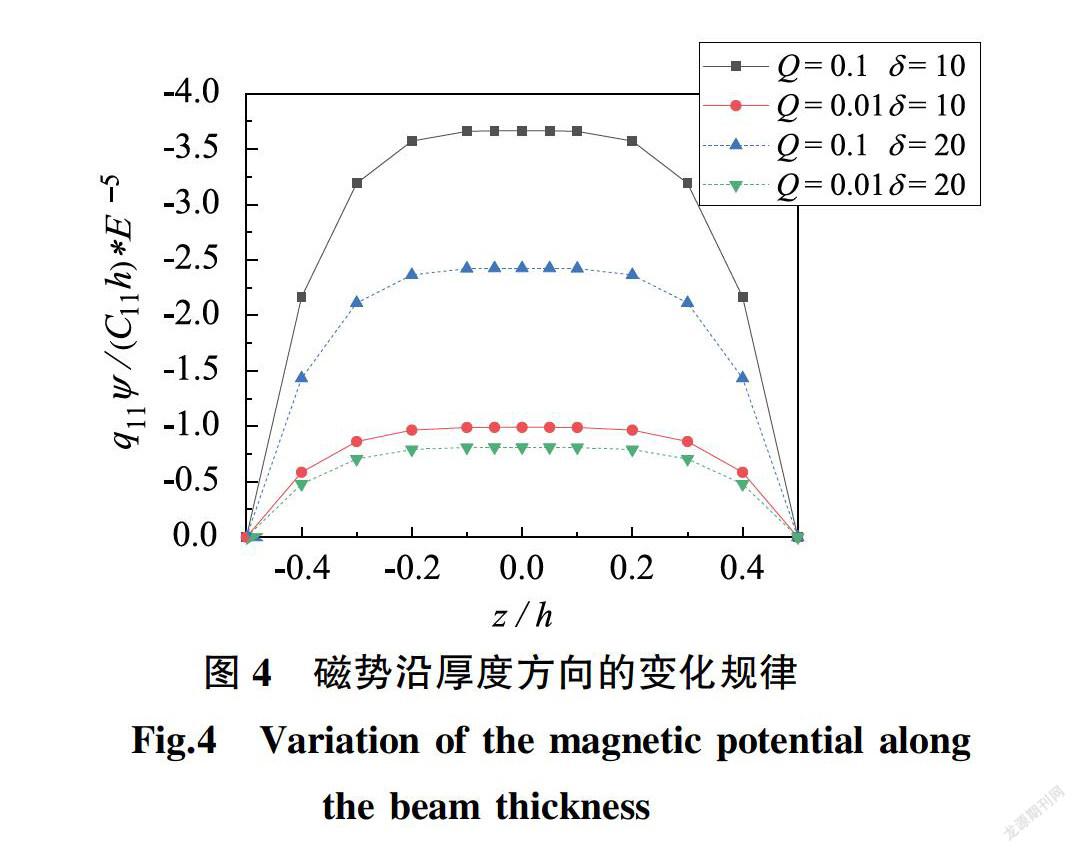
图2和图3分别给出了在h=0.5和Q=0.01的情形下，梁跨中的挠度在不同的跨高比下随磁场强度和电场强度的变化规律。由图2可以看出，在不同跨高比下，梁的挠度随磁场强度加大而减小，且变化较为平缓。从图3可知，在不同跨高比下，梁挠度随电场强度的增大而减小，但曲线一开始急剧下降，而后趋于平缓。

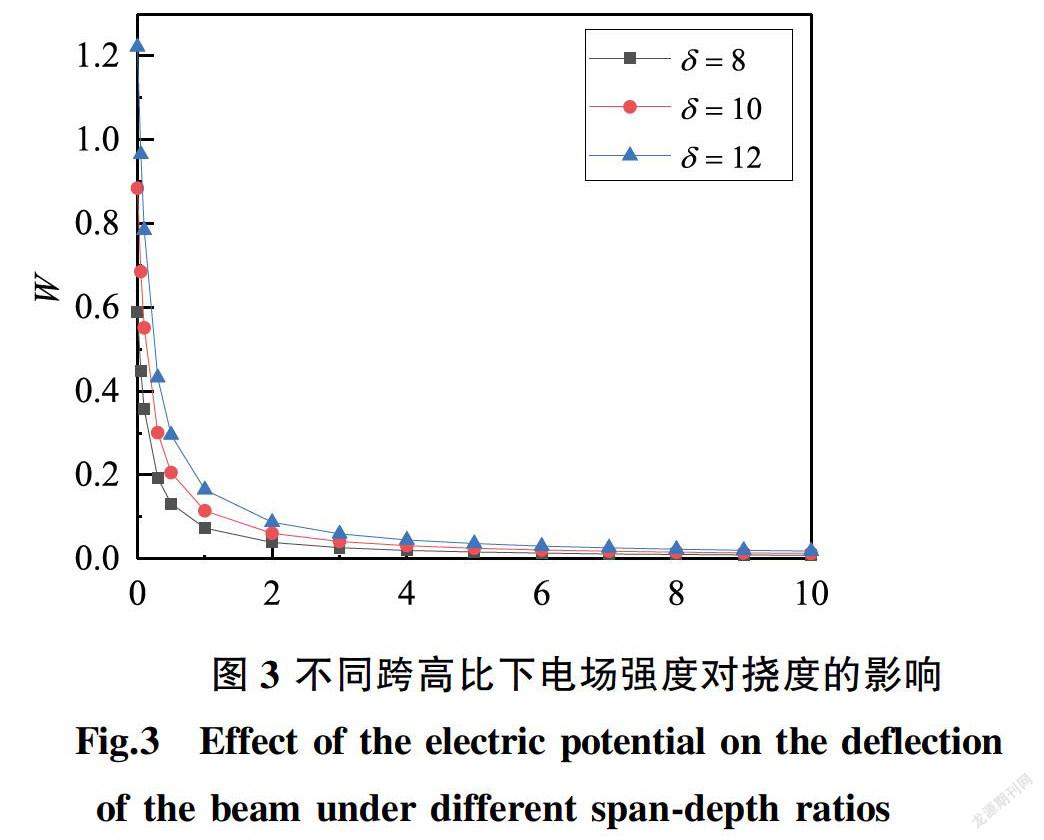
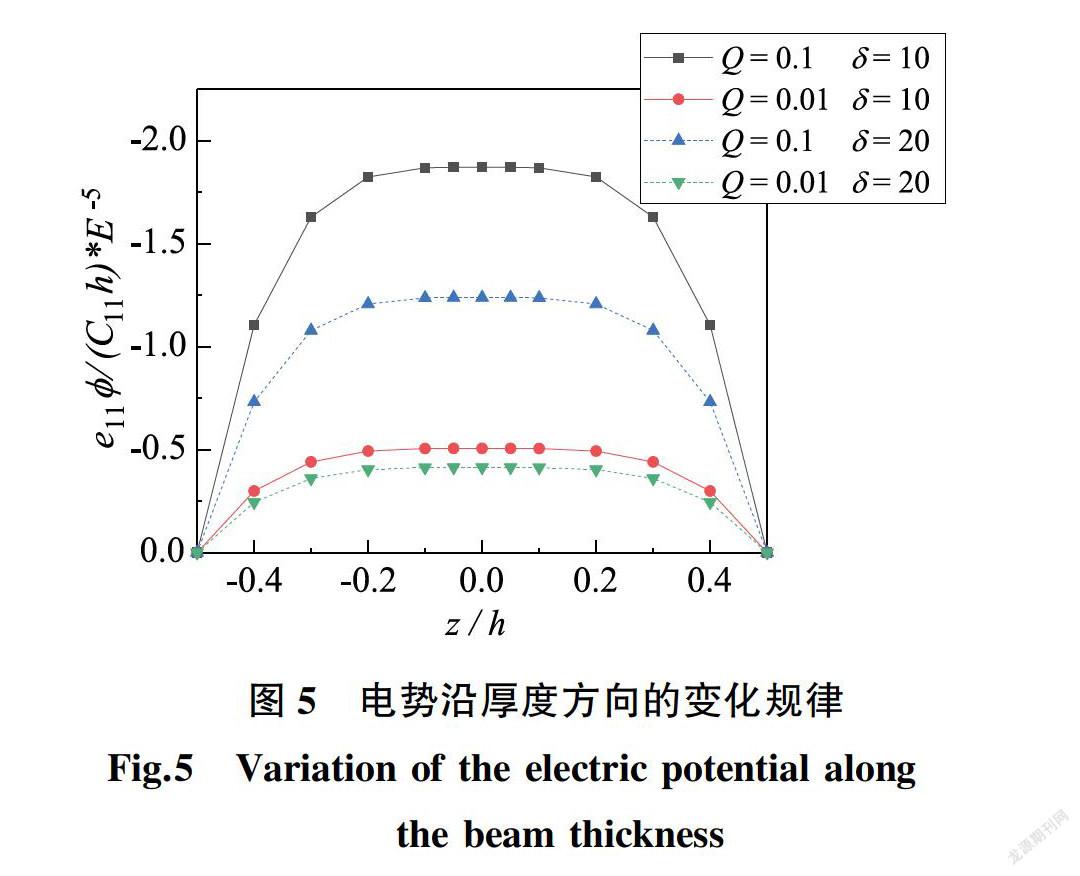
圖4和图5分别给出了在h=0.5，Ω=0，V=0和Q=0.01的情形下，磁势和电势沿梁厚度方向的变化特性。由图中可以看出，在机械荷载作用下，梁内部产生磁势和电势，且最大值处于梁的中性层上。磁势和电势由中间向两端减小，靠近两端的区域变化明显，而靠近中间区域变化相比而言相对平缓。

4 结语

本文研究了磁电弹性梁在力电磁载荷作用下的非线性静力响应。通过高阶剪切变形理论和Von Karman非线性理论建立了磁电弹性梁的非线性力学模型，探究了外荷载、梁的跨高比、磁场和电场对梁变形的影响，以及磁势和电势沿梁厚方向的变化规律。数值结果表明：

（1）在相同条件下，外荷载或跨高比的增大会极剧加大梁的变形程度，且具有明显的非线性特征。

（2）磁场和电场的改变对梁的挠度具有显著的影响，可以通过施加外磁场或外电场来控制结构的变形。

（3）在外荷载作用下，磁电弹性梁内部产生磁势和电势，且最大值发生梁的中性层上，可以利用力电磁的相互转换的这个特性对结构进行主动控制。

参考文献：

[1]江爱民，邱洪林，林定远. 均布荷载作用下简支磁电弹性梁的解析解[J]. 浙江工业大学学报， 2004（2）：123-128.

[2]江爱民，林定远，邱洪林. 均布荷载作用下悬臂磁电弹性梁的解析解[J]. 应用力学学报， 2004（4）：106-109.

[3]吴国泉，胡维新，江爱民. 悬臂磁电弹性梁自由端作用集中力问题的解析解[J]. 宁波大学学报（理工版）， 2005（2）：170-174.

[4]邱洪林， 江爱民. 线性电势和磁势边条下磁电弹性梁的解析解[J]. 宁波大学学报（理工版）， 2007（2）：240-244.

[5]Milazzo A， Orlando C. A beam finite element for magneto￣electro￣elastic multilayered composite structures[J]. Composite Structures， 2012， 94（12）：3710-3721.

[6]Huang D J， Ding H J， Chen W Q. Static analysis of anisotropic functionally graded magneto￣electro￣elastic beams subjected to arbitrary loading[J]. European Journal of Mechanics， A/Solids， 2010， 29（3）：356-369.

[7]Huang D J， Ding H J， Chen W Q. Analytical solution for functionally graded magneto￣electro￣elastic plane beams[J]. International Journal of Engineering Science， 2007， 45（2-8）：467-485.

[8]Annigeri A R， Ganesan N， Swarnamani S. Free vibration behaviour of multiphase and layered magneto￣electro￣elastic beam[J]. Journal of Sound and Vibration， 2007， 299（1-2）：44-63.

[9]Vinyas M， Kattimani S C. Static studies of stepped functionally graded magneto￣electro￣elastic beam subjected to different thermal loads[J]. Composite Structures， 2017， 163：216-237.

[10]Xu X J， Deng Z C， Zhang K， et al. Surface effects on the bending， buckling and free vibration analysis of magneto￣electro￣elastic beams[J]. Acta Mechanica， 2016， 227（6）：1557-1573.

[11]Ansari R， Gholami R. Nonlocal nonlinear first￣order shear deformable beam model for post￣buckling analysis of magneto￣electro￣thermo￣elastic nanobeams[J]. SCIENTIA IRANICA， 2016（No.6）：3099-3114.

[12]Xiao W， Gao Y， Zhu H. Buckling and post￣buckling of magneto￣electro￣thermo￣elastic functionally graded porous nanobeams[J]. Microsystem Technologies， 2019，25（6）：2451-2470.

[13]Alibeigi B， Beni Y T， Mehralian F. On the thermal buckling of magneto￣electro￣elastic piezoelectric nanobeams[J]. European Physical Journal Plus， 2018， 133（3）：133.

（責任编辑：曾 晶）

Nonlinear Static Analysis of Magneto￣electro￣elastic Beams Based

on Higher Order Shear Deformation Theory

XU Liangliang1， ZHENG Yufang1*， CHEN Changping2

（1. College of Civil Engineering， Fuzhou University， Fuzhou 350116， China;

2.School of Civil Engineering and Architecture， Xiamen University of Technology， Xiamen 361024， China）

Abstract：

Based on the higher order shear deformation theory and Von Karman nonlinear theory， the nonlinear model of magneto￣electro￣elastic beams was established. The nonlinear equational differential equations of magneto￣electro￣ elastic beams were derived by using Hamilton principle， and the nonlinear partial differential equations were solved through applying the Galerkin method. In the numerical calculations， the influences of the external load， span ratio， magnetic field and electric field on the nonlinear static response of magneto￣electro￣elastic beams were discussed.

Key words：

Reddy third￣order shear theory; Von Karman nonlinear theory; magneto￣electro￣elastic beam; Galerkin method