关于一类数列求和的解法探究

张俊畅 杨柳忠

(广东省大埔县虎山中学 514299)

求通项为等差数列与等比数列的积的数列的前n项和，是数列求和中的一种重要题型.在教学中，我们发现，此类问题常用错位相减法解决，解法比较单一，计算量大，合并化简时，学生很容易搞错，那么此类问题还有哪些解法,他们各自的优缺点在哪里，怎样进行合理的选择等等，此文将对此做些研究.

以2017年天津高考理科数学18题为例：已知{an}为等差数列，前n项和为Sn(n∈N*)，{bn}是首项为2的等比数列，且公比大于0，b2+b3=12,b3=a4-2a1，S11=11b4.

(1)求{an}和{bn}的通项公式；

(2)求数列{a2nb2n-1}的前n项和(n∈N*).

分析由题中的条件易求an=3n-2，bn=2n.我们来重点关注第二个问的求法，这里给出两种不同解法.

一、错位相减法

解设数列{a2nb2n-1}的前项和为Tn，由a2n=6n-2，b2n-1=2×4n-1，有a2nb2n-1=(3n-1)×4n，故

Tn=2×4+5×42+8×43+…+(3n-1)×4n，

4Tn=2×42+5×43+8×44+…+(3n-4)×4n+(3n-1)×4n+1，

上述两式相减，得

-3Tn=2×4+3×42+3×43+…+3×4n-(3n-1)×4n+1

所以，数列{a2nb2n-1}的前项和为

解法提炼错位相减法求和是求解由等差数列与等比数列的积构成的数列的和的标准解法，主要考查同学们数列公式的掌握程度和数式的运算化简能力.同学们在错位相减后用等比数列求和时容易把数列的项数搞错，还有运算化简很容易犯错，这也是这种方法的弊端.

二、公式法

我们发现由等差数列与等比数列的积构成的数列都可化为形如{(an+b)·qn-1}的形式，现在我们来详细研究此类数列的前n项和Sn的结构特点：

1.问题：设cn=(an+b)·qn-1，求数列的前n项和Sn.

2.猜想：观察上例，我们不难看到此类数列的前n项和Sn是一次函数与指数函数的乘积与一个常数的和，尝试几个例子后，也有相同的结论，那么此类问题的一般结论是什么？它们之间到底存在怎样的关联呢？

3.公式推导：记an=an+b，bn=qn-1则

Sn=a1b1+a2b2+…+an-1bn-1+anbn…①,

qSn=a1b2+a2b3+…+an-1bn+anbn+1…②.

由②-①得：

(q-1)Sn=-a1b1-d(b2+b3+…+bn)+anbn+1

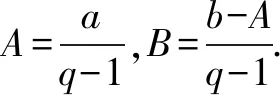
4.结论：形如{(an+b)·qn-1}的数列的前n项和是一次函数与指数函数的乘积减该一次函数的常数项.

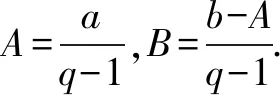
5.应用此结论解上题：

解设数列{a2nb2n-1}的前项和为Tn，由a2n=6n-2，b2n-1=2×4n-1，有a2nb2n-1=(3n-1)×4n.

设{(3n-1)×4n}的前n项和为Tn=(An+B)·4n-B,

则T1=a1=4A+3B=8…①.

∵T2=a1+a2=88,∴T2=32A+15B=88…②.

由①②解得：

也可以这样解：∵(3n-1)×4n=(12n-4)×4n-1，设其前n项和为Tn=(An+B)·4n-B，

在这里还得说明一下，由于此公式课本上并没有给出，所以在做解答题时不能直接使用，但我们可以按方法1的步骤求解后，用此法来检验最后结果的正误.当然在做此类问题的选择填空题上，直接运用公式法，可绕开中间繁琐的运算化简的过程，从而快速得出准确的结果，效果会比较好.

巴甫洛夫说过：“复杂现象只是逐步逐段的被科学所认识，但它总是越来越多地逐渐背科学完全掌握.”

我们在数学的学习与实践中要善于观察，求同存异，大胆猜想，勇敢探索，逐步逐段的接近真理，直至完全掌握它.这种对学生进行逐次渐进的解题意识和能力的培养，也正是新时期我们教育教学的一个努力方向.