思维风暴下的“构造之花”——赋值构造在代数式最值问题中的应用

孙如敏

(江苏省睢宁县第一中学 221200)

构造思想的核心是构造，构造是什么？怎么构造？构造作为一种手段，具有十分明确的目的，它与要认识和解决的数学问题紧密联系着.笔者在讲授函数最值时对构造的思想方法颇有感触，在课堂的教学过程中提出了若干种常规的方法，虽然这些常规手段是我们解决函数最值时的首当其冲应该想到的，不过对于一些颇为棘手的难题，当我们用常规方法不太好解决时，可以根据题目中的条件对目标代数式进行构造，正所谓正难则反，选择好的构造方法往往让我们觉得耳目一新.下面就笔者在讲授相关最值问题的一些案例和读者共享.

案例1 设二次函数f(x)=ax2+(2b+1)x-a-2(a,b∈R,a≠0)在[3,4]上至少有一个零点，求a2+b2的最小值.

下面一段文字是笔者对课堂实录的一部分.

T：二次函数f(x)=ax2+(2b+1)x-a-2(a,b∈R,a≠0)在[3,4]上至少有一个零点，意味着什么呢？

S：意味着此二次函数所对应的图象在[3,4]这个区间上有一个或者二个交点.

T：能否在演稿纸上把相应的示意图画出来呢？

S：(学生默默地拿笔在演稿纸上画图，时间大概二三分钟)……

T：学生把各自作图成果展示给大家伙看，一起总结分析(教师用投影仪把学生画的图展示出来).我们发现满足题目条件的图象种类较多，每一种图象的情况找出相应的限制条件.

S：经过刚才的讨论情况，发现满足条件的二次函数图象情况较多，每一种情况也相对复杂些，把这么多种情况都考虑全面了，估计将耗费更多的时间和精力.

T：想一想有没有更加好的办法呢?

S：难不成我们可以利用条件直接去构造不成？

T：我们可以试试通过参变分离的方式构造出有关a2+b2的方程或者不等式来分析.

S：由已知得，设t为二次函数在[3,4]上的零点，则有at2+(2b+1)t-a-2=0，从而有

at2+2bt+t-a-2=0，即有2-t=[a(t2-1)+2bt].现在只能分离到这一步了，虽然本意想参变分离，但是尽我所能只能分到这一步了.

T：你们已经做得很好了，想彻底地做到参变分离的确有点困难，想想我们还可以通过其它什么方式做到参变分离呢？(留足够时间思考)

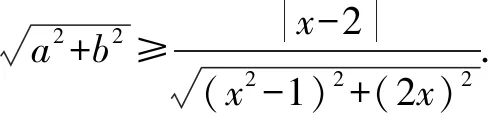
小结：上述案例就是用构造的方式求代数式的最值或者范围问题，但构造的方式方法是多种多样的，至于什么样方式得看具体的条件来处理.有时候当一种方法失败后就得学会在失败的基础上进行反思，不断修正从而找到正确的构造方法.下面我们再欣赏一个案例：

案例2 设二次函数f(x)=2px2+qx-p+1,当|x|≤1时，f(x)≥0恒成立，求p+q的最大值.

下面一段文字是笔者对课堂实录的一部分.

S：此题的条件和案例1所给条件从逻辑上讲是对立的，但解题的方式恰恰是类似的，都可以从图象入手，从正面考虑二次函数在区间[-1,1]上图象永远在x轴的上方或者在其上方时最多有一个交点，用不等式或者不等式组去限制时情况较复杂，所以也可以和上述案例一样，采用构造的方式构造出有关p+q的代数式进而求出相应的范围.

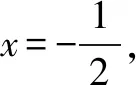
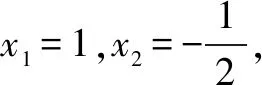
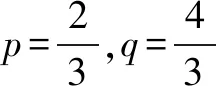
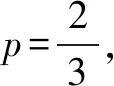
S:这种赋值构造的理由让人受益匪浅，值得借鉴，对于代数式求最值或者证明其满足某个范围的时候，如果从正面考虑比较复杂，正所谓正难则反，通过构造的确是一个不错的思路，其中赋值构造的办法让人眼界大开，很是不错.

在解题的过程中有些人在达到目标和解答题目方面比较成功，另一些则没有那么成功，数学教育的成功之处就是在于让学生在解题的过程中充分体验各种情绪，如失望，等待，焦虑，恐惧，期望，希望，激动，兴奋.在对难度较大的数学题目面前是各种方法的较量与博弈，而在各种方法的博弈中，思维风暴下崩发出的构造之花更是锦上添花！