空间低温杜瓦瓶凯夫拉支撑结构多约束优化设计

王国鹏，李建国，赵雅楠，洪国同

(1. 中国科学院理化技术研究所空间功热转换技术重点实验室，北京100190；2. 中国科学院大学，北京100190)

0 引 言

对低温制冷技术的需求随着红外探测、低温超导、航空航天等前沿科技的发展越来越广泛。传统低温制冷技术包括机械制冷机以及低温液体贮存杜瓦瓶。其中机械制冷机由于存在振动、功耗需求较大以及低温下制冷量较小等限制，难以在一些特殊的空间场合应用，因此低温液体贮存杜瓦瓶依然是空间主流制冷技术[1]之一。在低温杜瓦瓶设计中，漏热损失是衡量其性能的重要指标，而通过支撑结构进入杜瓦瓶的热量占到了漏热损失的30%以上。除此之外，支撑结构还必须保证系统结构具有足够的力学稳定性。这就要求杜瓦瓶结构本身足够稳定，同时，所采用的支撑材料在低温下具有较高强度以及较低的热导率。而针对空间应用的低温杜瓦瓶其支撑材料还要求具有较轻的质量以降低发射成本[2]。传统低温杜瓦瓶的支撑结构多从减小漏热损失角度考虑，因而在其力学性能方面做出了一定妥协，能够基本满足地面使用要求，却难以适应航天器发射及空间复杂外部环境。而目前对于低温杜瓦瓶支撑结构的热力学性能的耦合研究涉及较少，绝大多数分析都将支撑结构的力学分析和热学性能分别进行研究。Kittel[4]对柔性绳索结构以及杆系结构的支撑采用一维简化模型进行分析，并在此基础上比较了二者的漏热损失。Bushnell[5]对火箭低温燃料贮箱采用的刚性、柔性以及被动轨道断开式管型支撑(Passive orbital disconnect struct,PODS)三种支撑的性能进行了比较分析。Hopkins[6]则以COBE卫星杜瓦瓶为背景，分别采用柔性支撑带及PODS两种支撑形式进行了结构设计，并对两种形式的力学性能及漏热损失分别进行分析，认为柔性支撑带更适合于液氦及液氢杜瓦瓶，而PODS结构更适合于液氮及液氧杜瓦瓶[3-6]。吴红[7]针对某超导磁体设计了采用柔性拉带的冷质量支撑结构，建立了相应的力学模型，在此结构上分析了其漏热损失。除此之外，还有学者针对不同的支撑形式及材料进行了较多研究[8-10]。近年来，一种新型的高分子材料对位芳纶纤维(凯夫拉),由于其极低的热导率以及优异的力学性能而在低温系统中获得了越来越多的关注。其与不锈钢材料的性能对比如表1所示。英国的詹姆·斯克拉克·麦克斯韦望远镜(JCMT)、美国SABER红外探测器组件等结构均采用了凯夫拉纤维并设计了相应的支撑形式[11]。

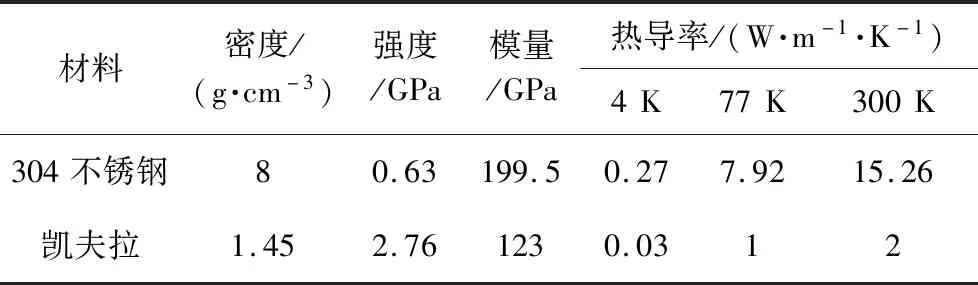
表1 材料性能对比Table 1 Comparison of the material property

图1所示为凯夫拉绳索的拉伸试验，图1(a)为分别采用了四股及两股纤维原丝合股成的绳索及测试工装，图1(b)为通过拉伸试验机测出的拉伸试验曲线。从试验结果来看，2股凯夫拉原丝合股的最大拉力达到了380 N，而4股凯夫拉原丝合股的最大拉力达到了大约980 N(实际最大拉力与纤维合股时加捻程度也有关系，此处仅为说明凯夫拉力学性能，工程应用时应加以注意),充分表明了凯夫拉纤维优越的力学性能。

图1 凯夫拉纤维测试工装及拉伸曲线Fig.1 Test specimens and tensile curve of the Kevlar fiber

文章针对空间用小型低温杜瓦瓶采用凯夫拉纤维设计了绳索支撑结构，进行了纤维的拉伸试验，并从漏热损失和力学性能耦合角度建立了数学模型，在其固有频率、热应力以及发射环境应力约束条件基础上，通过一种新的“离散点加密”的约束优化方法，对其进行了最优化设计。

1 支撑结构设计及数学模型构建

1.1 模型构建与简化

杜瓦瓶内胆外筒均为圆柱状结构，支撑结构采用空间杜瓦瓶常见的柔性绳索上下对拉形式，绳索呈一定空间角，能够承受来自三个方向上的拉力。上、下半部分各六根绳索与杜瓦瓶内胆接触位置分别在同一横截面内。在这一思路下，可得系统支撑结构的物理模型如图2(a)所示，其实际验证结构如图2(b)所示。结构由外筒、凯夫拉绳索、内胆以及凯夫拉绳索与杜瓦瓶外筒及内胆的连接接头组成。

为便于分析，将杜瓦瓶实际结构进行适当简化。忽略支撑结构的冷端与热端接头，认为二者分别铰接在杜瓦瓶外筒和内胆上；由于凯夫拉绳索质量极轻，因此在分析中将其质量忽略，在外筒及内胆结构参数确定的情况下，可得出确定支撑结构所需的设计参数为：杜瓦瓶内胆支撑结构接触点上端点到杜瓦瓶重心所在横截平面的距离Ls；支撑绳索水平角θ；支撑绳索倾斜角γ；支撑绳索的横截面积A；每个支撑上所需施加的预紧力F，即确定支撑结构需要上述Ls，θ，γ，A，F共五个参数。在上述假设下，通过支撑结构的漏热量可以表示为：

q=NKAΔT/L

(1)

式中：N为支撑数目，K为凯夫拉绳索热导率，A为绳索横截面积，L为凯夫拉绳索长度，ΔT为绳索两端温差。

根据图2所示模型，可得出绳索长度L为平面角θ及倾斜角γ的函数：

(2)

图2 系统实际支撑结构图Fig.2 Actual support structure of the system

1.2 约束条件

1.2.1热应力约束

低温燃料贮箱在加注低温液体时绳索结构应满足一定的热应力约束条件[12]。考虑由于杜瓦瓶内胆、外筒的热膨胀系数不同而在支撑结构上产生的应力，表达式如式(3)～(6)所示：

(3)

σpre=Eε2+F/A

(4)

σpre/σmax≤1

(5)

εr=ε2+F/EA>0

(6)

其中，ε2为贮箱沿绳索方向上的应变，α2为贮箱材料的热膨胀系数，σpre为绳索上的应力值，式(5)表示绳索上的应力值应当小于抗拉强度，式(6)表示绳索上的应变不能为零。而由于凯夫拉绳索在低温下会发生膨胀，其应变应当被考虑进去，表达式如式(7)所示：

(7)

其中，α1为凯夫拉材料的热膨胀系数。因此表达式(4)、(6)修正为：

σpre=E(ε2+ε1)+F/A

(8)

(9)

1.2.2发射环境下的应力约束

空间用杜瓦瓶要经历严苛的发射环境，在发射环境下，系统在水平及竖直方向要承受大约10g的加速度。此时需要保证受拉绳索应力值σlau小于最大许用应力，同时绳索上的应变ecri不能为零(即绳索不能松弛)。因此，绳索支撑结构应满足一定的应力约束条件,表达式如式(10)～(13)所示:

σlau/σmax≤1

(10)

σlau=Eelau

(11)

(12)

(13)

(14)

(15)

其中，elau,eaxi,elat分别为绳索上的总应变以及沿杜瓦瓶中轴线方向和垂直中轴线方向的应变分量，Q为重力加速度倍数，在式(12)及式(13)中，总应变作保守处理，即横向应变、轴向应变绝对值与预紧力应变三者之和大于零，而预紧力应变与横向应变及轴向应变之差大于零。式(14)、式(15)分别为绳索在加速度条件下的轴向应变与径向应变表达式，由结构在径向和轴向的应变能公式得到。此外，在进行分析时，模型还应当满足以下自然条件限制：

(16)

1.2.3固有频率约束

空间用低温杜瓦瓶其固有频率应当满足一定要求，以避免在外界环境下发生共振而使结构遭到破坏。系统固有频率与支撑结构的形式密切相关。将结构模型置于图2所示坐标系下，根据第1.1节中所做假设，系统的总动能及应变能可以表示为：

(17)

(18)

x=Xsin(ωt+φ)

(19)

其中，X与ω为主振型与固有频率，根据主振动表达式可得最大动能与势能分别为

(20)

由于主阵型之间的正交性，系统的动能(势能)等于各阶主振动单独存在时系统的动能(势能)之和，系统机械能守恒

T=U

(21)

根据式(22)可得出系统某阶主振动的固有频率为

(22)

固有频率约束条件可以表示为

ωmin≥fs

(23)

式中:fs为固有频率下限值。

2 多约束优化设计方法及求解分析

由第1节分析可知，支撑结构的漏热损失受结构参数及材料物性参数限制，其优化需要满足集中约束条件的限制，因而模型可以量化为多约束条件下的优化设计问题。其中以漏热损失作为被优化函数，而此优化函数受到条件(5)、(6)、(9)、(10)、(12)、(13)、(16)、(23)约束，其中式(23)中固有频率约束6个，式(16)中共5个约束条件，因此函数共受17个约束条件限制，并且其中约束条件多为非线性。针对此类约束优化问题，有多种方法可以进行，例如可行方向法、罚函数法、二次规划法等[14-16]，然而这些优化方法需要选取满足约束条件的初始值，并且往往只能给出初始值附近的局部最优值。支撑结构模型中共5个变量，约束条件较多，并且满足约束条件的初始值范围较大，直接选取某一初始值进行计算，难以得出约束条件范围内的最优解。因此，对模型采取所谓“离散点加密”的方法：首先对5个变量中的每一自变量，在其取值范围内从下限到上限按顺序取有限个值N，此5个自变量将会组成N5组初始值，再将这些初始值按满足约束条件与否进行筛选，选出满足所有约束条件的初始值组合，这些组合称为“离散点”，对筛选出的所有离散点组合分别求解最优值，再将所有最优值进行比较，选出最小值作为第一轮计算的最优值，此后进行第二轮计算，此轮计算中，将N的个数加倍，也即加密离散点个数，而后重新进行计算，以后的每轮计算中，每次将N的个数加倍，重复计算最优值，当计算出的最优值不再随加密次数发生变化时，认为所取得的优化值为约束条件范围内的最优值。这种方法相当于通过取遍满足条件的取值组合来比较得出最优结果，从而避免了因局部优化导致的最优值遗漏。图3为程序计算框图。

图3 算法流程图Fig.3 Flow chart of the algorithm

优化函数的表达式归结如下：

minf(Z),Z∈Rn

s.tgi(Z)≤0,j=1,2,…,p

(24)

式(24)中，f(Z)为目标函数，即需要被优化的参数，此处为支撑结构的漏热损失，gi(Z)为受约束的边界条件，此处为支撑结构的发射应力及热应力约束条件以及固有频率约束条件。支撑结构的目标函数为式(1)，而式(5)、(6)、(9)、(10)、(12)、(13)、(16)、(23)构成本方法中的约束条件。在此将边界条件中的五个参数表示为向量Z：

(25)

则目标函数漏热量可以表示为：

q=f(Z)

(26)

所有边界条件整合后如式(27)所示。通过Matlab软件工具箱内的fimcon函数作为局部优化函数，同时编写离散点加密程序进行计算。在给定一组初值的情况下，可得到目标函数的变化值如图4所示，设计参数的迭代变化值如图5所示，各约束条件的迭代变化值如图6所示。

(27)

图4 漏热损失Fig.4 Heat leakage

图5 设计参数计算结果Fig.5 Computations of design parameters

图6 约束条件值计算结果Fig.6 Computations of the constraint values

从图4可以看出，在自变量离散点个数从0增加到5时，支撑结构漏热损失从0.0073 W逐步下降到0.0046 W，由于共5个设计参数，此时所计算的参数组合数共55组；当离散点个数从5增加到11时，参数组合数变为115组，而漏热损失的计算值已经基本不再发生变化，由于逐步进行离散点加密已不能改变漏热量的优化值，此时认为漏热损失已达到全局最优值。图5为5个设计参数随离散点增加的变化曲线，为表达方便，各参数分别作了按比例放大或缩小处理。对比图4可以看出，当漏热损失随离散点数增加趋于平稳时，设计参数并没有一同趋于某一平稳值，而是在不同离散点处发生不规则跳动，但所有取值均处于取值范围内。如Ls取值随离散点个数增加呈现出先增加后下降进而进一步增加的趋势，无明显规律可循。图6为各约束条件计算值随离散点数增加的变化曲线，改变后的约束条件值中，各阶固有频率均大于100 Hz，均满足大于100 Hz的下限，热应力约束条件值以及发射应力约束条件值在0.2～0.5范围内波动，均小于1。但同图5类似，随离散点数增加同样没有明显规律，即使在离散点加密到目标函数优化值已不再变化时，设计参数和约束条件值依然有剧烈跳动。

图5及图6的计算结果表明了两点，首先，在多个非线性的约束条件下，目标函数的局部最优值分布很广，并且局部最优值所对应的设计参数之间并无太大关系，从而证明了从单一初始值进行优化寻找最优值可能会导致最优值遗漏，而采用“离散点加密”方法通过最大限度地获取初始值组合并通过比较局部最优值从而得出取值范围内最优值方法的有效性。再者，图4所示结果也表明了目标函数取得的最优值可能对应存在多组满足约束条件的设计参数。在这种情况下，可以根据力学性能要求或者实际结构特点来决定所采用的最佳设计参数组合，同时也表明了采用取值范围内离散点加密计算的必要性。通过计算点加密来对所有可能的局部优化值进行扫描，这样能够避免采用单组优化函数所造成的优化值遗漏，从而找出约束条件取值范围内的最优值。

3 结 论

对一种空间低温杜瓦瓶支撑结构采用高强度低热导率的凯夫拉纤维绳索进行了设计，并进行了合股纤维的拉伸试验，在此基础上建立了支撑结构在发射环境下的热力学优化模型，利用离散点加密联合局部优化函数的方法得出了最优设计。结果表明此种优化分析方法能够在满足力学环境条件的前提下找出全局范围内的最小的漏热损失，同时可根据设计要求来选择最佳设计参数。本文中的建模及优化方法将杜瓦瓶支撑结构的热学性能与力学设计耦合进行考虑，为空间杜瓦瓶的设计提供了参考。