点、直线、平面之间的位置关系常见典型考题赏析
■张文伟
题型1:平面的基本性质及应用
证明点共线问题,就是证明三个或三个以上的点在同一条直线上,证明三线共点问题,一般先证明待证的三条直线中的两条相交于一点,再证明第三条直线也过该点。证明点线共面问题主要有两种方法:①首先由所给条件中的部分线(或点)确定一个平面,然后再证其余的线(或点)在这个平面内;②将所有条件分为两部分,然后分别确定平面,再证两平面重合。
例1如图1 所示, 在 正 方 体ABCD-A1B1C1D1中,E,F分 别 是AB和AA1的中点。
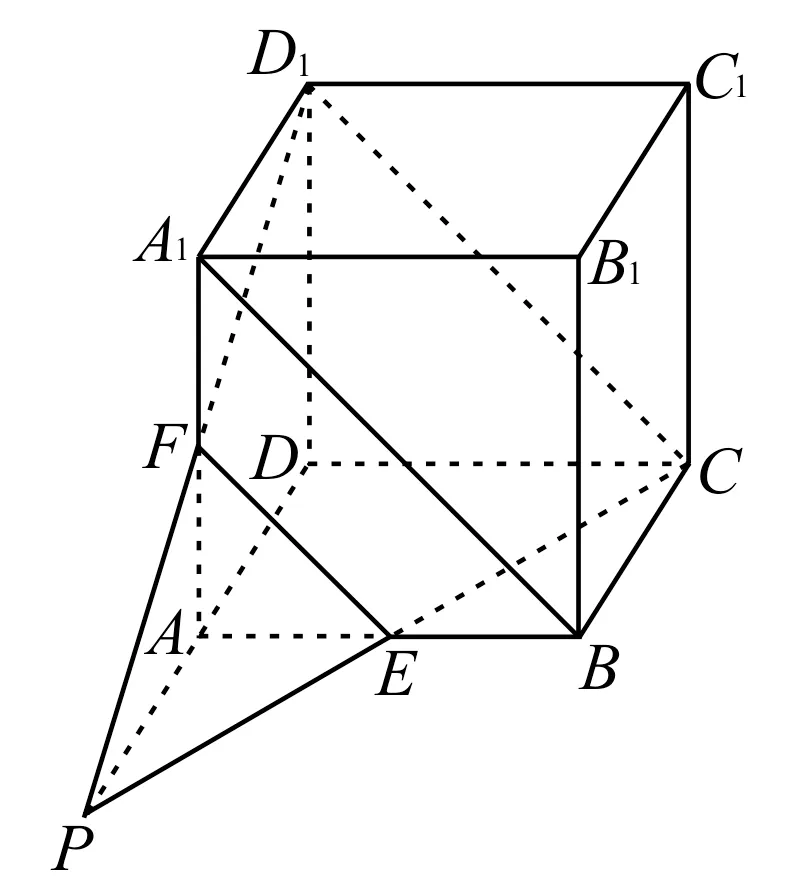
图1
求证:(1)E,C,D1,F四点共面。
(2)CE,D1F,DA三线共点。
证明:(1)连接EF,CD1,A1B。因为E,F分别是AB,AA1的中点,所以EF∥BA1。
又A1B∥D1C,所以EF∥CD1,所以E,C,D1,F四点共面。
(2)因为EF∥CD1,EF<CD1,所以CE与D1F必相交。设交点为P,则由P∈CE,CE⊂平面ABCD,得P∈平面ABCD。同理可得,P∈平面ADD1A1。又平面ABCD∩平面ADD1A1=DA,所以P∈直线DA,所以CE,D1F,DA三线共点。
跟踪训练1:如图2所示,在空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2。

图2
(1)求证:E,F,G,H四点共面。
(2)设EG与FH交于点P,求证:P,A,C三点共线。
提示:(1)因为E,F分别为AB,AD的中点,所以EF∥BD。在△BCD中,由,可得GH∥BD,所以EF∥GH,所以E,F,G,H四点共面。
(2)因为EG∩FH=P,P∈EG,EG⊂平面ABC,所以P∈平面ABC。同理可得,P∈平面ADC,所以P为平面ABC与平面ADC的公共点。 又平面ABC∩平面ADC=AC,所以P∈AC,故P,A,C三点共线。
题型2:异面直线所成的角
求异面直线所成的角常用平移法,平移法有三种类型,即利用图中已有的平行线平移、利用特殊点(线段的端点或中点)作平行线平移、利用补形平移。求异面直线所成角的步骤:一作,即根据定义作出异面直线所成的角;二证,即证明作出的角就是异面直线所成的角;三求,即解三角形,求出作出的角。如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角。判断空间两条异面直线的方法:利用判定定理,即平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线;利用反证法,即证明两条直线不可能平行、相交或证明两条直线不可能共面,从而可得两条直线异面。
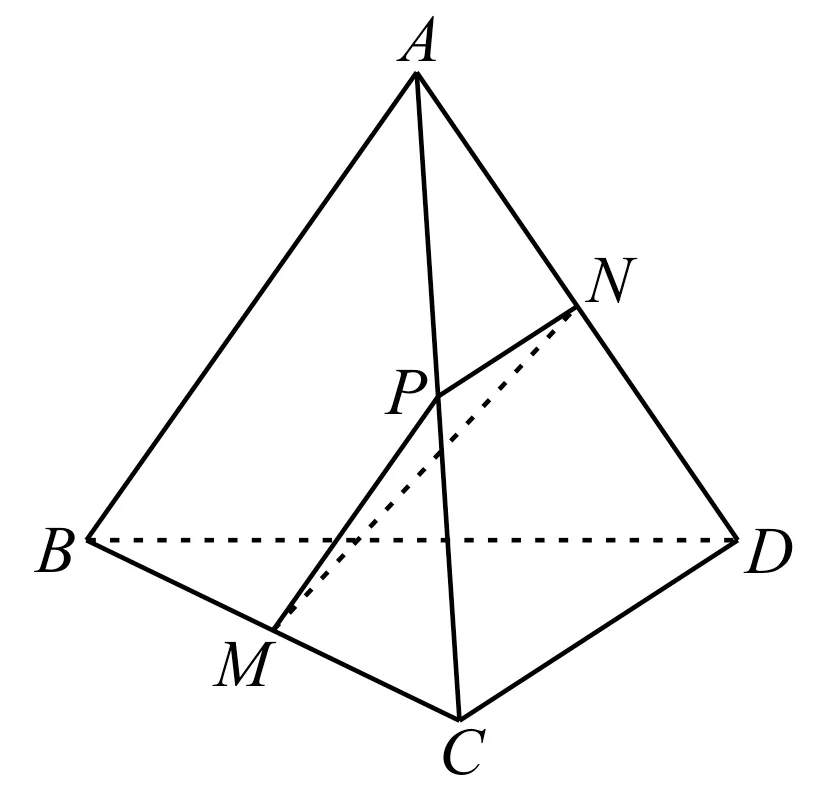
图3
例2如图3,已知三棱锥A-BCD中,AB=CD,且直线AB与CD所 成的角为60°,点M,N分别是BC,AD的中点,则异面直线AB与MN所成角的大小为____。
解:取AC的中点为P,连接PM,PN,则PM∥AB且PM=AB,PN∥CD且PN=CD,所以∠MPN或其补角为AB与CD所 成 的 角,可 得∠MPN=60°或∠MPN=120°。
因为PM∥AB,所以∠PMN或其补角就是AB与MN所成的角。
因为AB=CD,所以PM=PN。 若∠MPN=60°,则△PMN是等边三角形,所以∠PMN=60°,所以AB与MN所成的角为60°。若∠MPN=120°,则∠PMN=30°,所以AB与MN所成的角为30°。
综上可知,异面直线AB与MN所成的角为30°或60°。
跟踪训练2:在空间四面体ABCD中,E,F分别为AD,BC的中点,AB=CD,且AB⊥CD,则异面直线EF与AB所成角的大小为( )。
A.6πB.4π
C.3πD.2π
提示:取BD的中点为O,连接OE,OF(图略)。因为E,F分别为AD,BC的中点,AB=CD,所以EO∥AB,OF∥CD,且EO=OF=CD。又因为AB⊥CD,所以EO⊥OF,可知∠OEF为异面直线EF与AB所成的角。由△EOF为等腰直角三角形,可得∠OEF=。应选B。
题型3:线面平行关系的基本问题
证明直线与平面平行,一般有以下几种方法:①用定义直接判断,一般用反证法;②用判定定理证明,关键是在平面内找(或作)一条直线与已知直线平行,证明时注意用符号语言叙述证明过程;③应用两平面平行的性质,即两平面平行时,其中一个平面内的任何直线都平行于另一个平面。证明平面与平面平行,一般有以下几种方法:①利用定义,即证明两个平面没有公共点(不常用)。②利用面面平行的判定定理(主要方法)。③利用垂直于同一条直线的两平面平行(客观题可用)。④利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个平面平行(客观题可用)。
例3如图4 所示,在 正 方 体ABCDA1B1C1D1中,O为 底 面ABCD的 中 心,P是DD1的中点,设Q是CC1上的点,当点Q____时,平面D1BQ∥平面PAO。(只填序号)
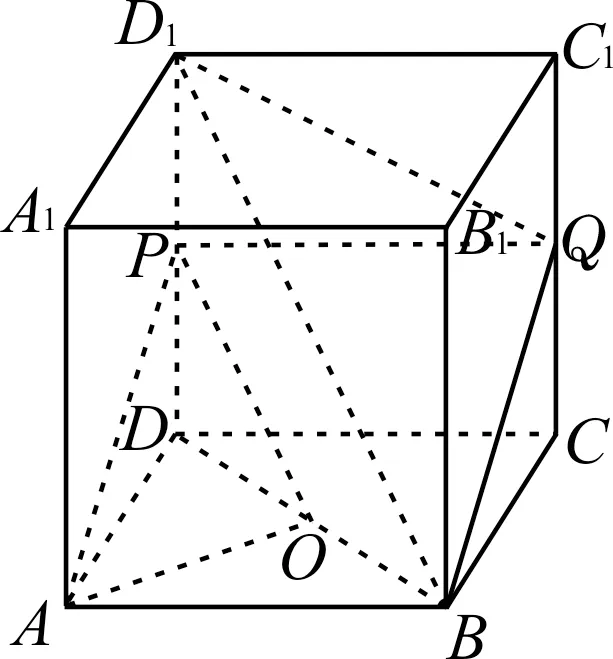
图4
①与C重合,②与C1重合,③为CC1的三等分点,④为CC1的中点。
解:在正方体ABCD-A1B1C1D1中,因为O为底 面ABCD的 中 心,P是DD1的 中点,所以PO∥BD1。当点Q为CC1的中点时,PQ■AB,则四边形ABQP是平行四边形,所以AP∥BQ。
因为AP∩PO=P,BQ∩BD1=B,AP、PO⊂平 面PAO,BQ、BD1⊂平 面D1BQ,所以平面D1BQ∥平面PAO。答案为④。
跟踪训练3:如图5,四边形ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点。
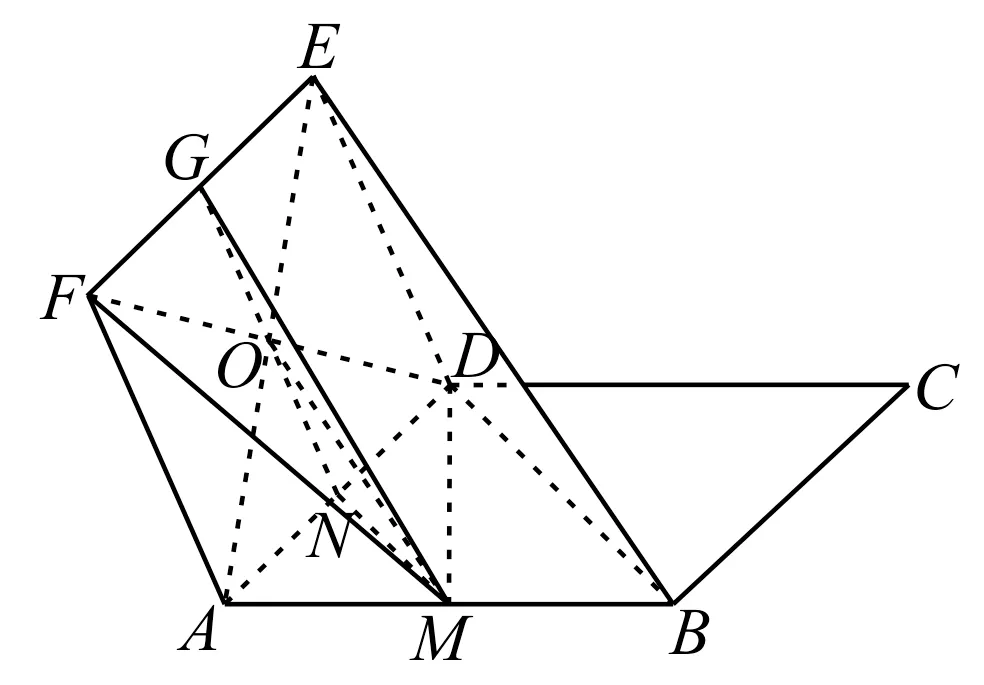
图5
求证:(1)BE∥平面DMF。
(2)平面BDE∥平面MNG。
提示:(1)连接AE,则AE必过DF与GN的交点O,连接MO,则MO为△ABE的中位线,所以BE∥MO。 因为BE⊄平面DMF,MO⊂平 面DMF,所 以BE∥平 面DMF。
(2)因为N,G分别边AD,EF的中点,所以DE∥GN。又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG。
因为M为AB的中点,N为AD的中点,所 以MN为△ABD的 中 位 线,所 以BD∥MN。因为BD⊄平面MNG,MN⊂平面MNG,所以BD∥平面MNG。
又DE与BD为平面BDE内的两条相交直线,所以平面BDE∥平面MNG。
题型4:线面垂直关系的基本问题
证明直线和平面垂直的常用方法:①利用线面垂直的定义;②利用判定定理;③利用平行线垂直平面的传递性(a∥b,a⊥α⇒b⊥α);④利用面面平行的性质(a⊥α,α∥β⇒a⊥β);⑤利用面面垂直的性质。证明面面垂直的常用方法:①利用定义(直二面角)。②利用判定定理,即通过直线与平面垂直来证明平面与平面垂直。
例4已知m,n是空间中两条不同的直线,α,β为空间中两个互相垂直的平面,则下列命题正确的是( )。
A.若m⊂α,则m⊥β
B.若m⊂α,n⊂β,则m⊥n
C.若m⊄α,m⊥β,则m∥α
D.若α∩β=m,n⊥m,则n⊥α
解:在A 中,若m⊂α,则直线m和平面β可能垂直,也可能平行或相交,A 不正确。在B中,直线m与直线n的关系不确定,可能平行,也可能相交或异面,B 不正确。在C中,若m⊥β,则m∥α或m⊂α,又m⊄α,故m∥α,C正确。在D 中,缺少条件n⊂β,D 不正确。应选C。
跟踪训练4:如图6,在四棱锥P-ABCD中,△PAB与△PBC是 正 三 角 形,平 面PAB⊥平面PBC,AC⊥BD,则下列结论不一定成立的是( )。

图6
B.PD⊥平面ABCD
C.AC⊥PD
D.平面PBD⊥平面ABCD
提示:对于A,取PB的中点O,连接AO,CO,在四棱锥P-ABCD中,由△PAB与△PBC是正三角形,可得AO⊥PB,CO⊥PB。因为AO∩CO=O,所以PB⊥平面AOC。因为AC⊂平面AOC,所以PB⊥AC,A 正确。对于B,设AC∩BD=M,连接PM,因为△PAB与△PBC都是正三角形,所以PA=PC,由此可得PM⊥AC,所以PD与AC不垂直,所以PD⊥平面ABCD不成立,B 不正确。对于C,因为PB⊥平面AOC,AC⊂平面AOC,所以AC⊥PB。因为AC⊥BD,PB∩BD=B,所以AC⊥平面PBD。又因为PD⊂平面PBD,所以AC⊥PD,C成立。对于D,因为AC⊥平面PBD,AC⊂平面ABCD,所以平面PBD⊥平面ABCD,D 成立。应选B。
题型5:线面角与二面角的问题
(1)求直线和平面所成角的关键是确定斜线在平面内的射影,射影一般都要确定一些特殊的点,如中心、垂心、重心等。(2)求二面角的步骤:一作,即作出平面角,作平面角时,一定要注意顶点的选择;二证,即证明所作的角就是二面角的平面角;三求,即将作出的角放在三角形中,计算出平面角的大小。
例5把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥的体积最大时,直线BD和平面ABC所成的角的大小为( )。
A.2πB.3π
C.4πD.6π
细菌溶解产物胶囊防治儿童反复呼吸道感染有效性和安全性的Meta分析 ………………………………… 戎 萍等(12):1702
解:如图7 所示,由三棱锥B-ACD的体积公式可知,当平面BAC⊥平面DAC时,三棱锥B-ACD的体积最大。
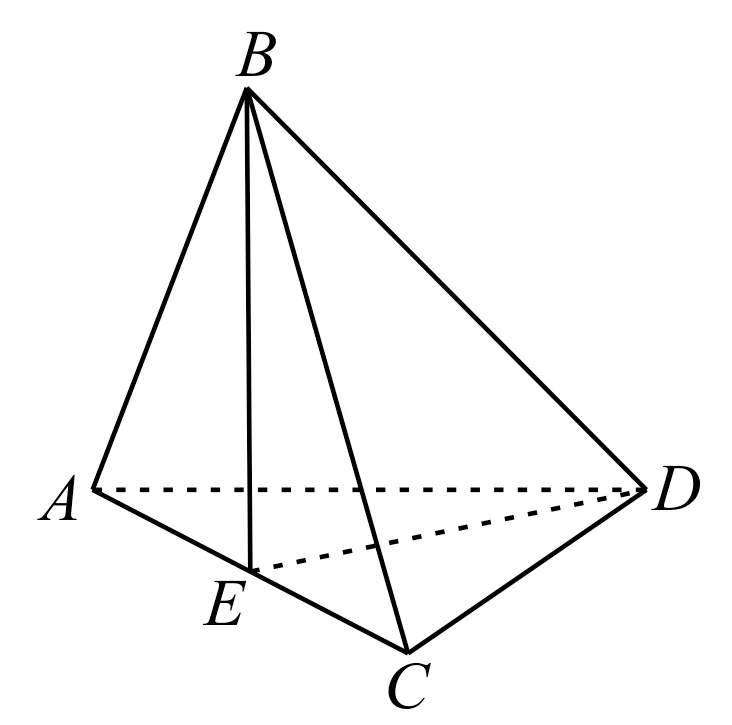
图7
取AC的中点为E, 则BE⊥ 平 面DAC,可知直线BD和平面ABC所成的角为∠DBE。
由题意可得cos∠DBE=,故∠DBE=。应选C。
跟踪训练5:如图8 所示,在正方体ABCD-A'B'C'D'中,二面角D'-AB-D的大小是( )。
A.6πB.4π
C.3πD.2π

图8
提示:连接AD'。由正方体的性质易知AB⊥平面ADD'A',则AB⊥AD,AB⊥AD',可知∠D'AD就是二面角D'-AB-D的平面角。 由四边形ADD'A'为正方形,可知∠D'AD=,即二面角D'-AB-D的大小是。应选B。
题型6:立体几何中的最值问题
立体几何中的最值问题一般涉及距离、面积、体积、角度等,此类问题多以规则几何体为载体,涉及几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等。解决此类问题一般可从两个方面思考:一是函数法,建立所求的目标函数,利用函数的最值求解;二是直接法,根据几何体的结构特征或平面几何中的相关结论,直接判断最值。
例6如图9所示,在四面体ABCD中,AB=CD=2,直线AB与CD所成的角为90°,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是 。

图9
解:因为直线AB∥平面EFGH,且平面ABC∩平面EFGH=HG,所以HG∥AB。同理可得,EF∥AB,FG∥CD,EH∥CD。所以FG∥EH,EF∥HG,可 知 四 边 形EFGH为平行四边形。
因为AB⊥CD,所以四边形EFGH为矩形。设=x(0≤x≤1),则FG=2x,易得HG=2(1-x)。
由上可得S四边形EFGH=FG×HG=4x(1。 由二次函数的图像与性质可得,当时,四边形EFGH面积的最大值为1。
跟踪训练6:如图10 所示,已知正方体ABCD-A1B1C1D1的棱长为1,每条棱所在直线与平面α所成的角都相等,则平面α截此正方体所得截面面积的最大值为( )。
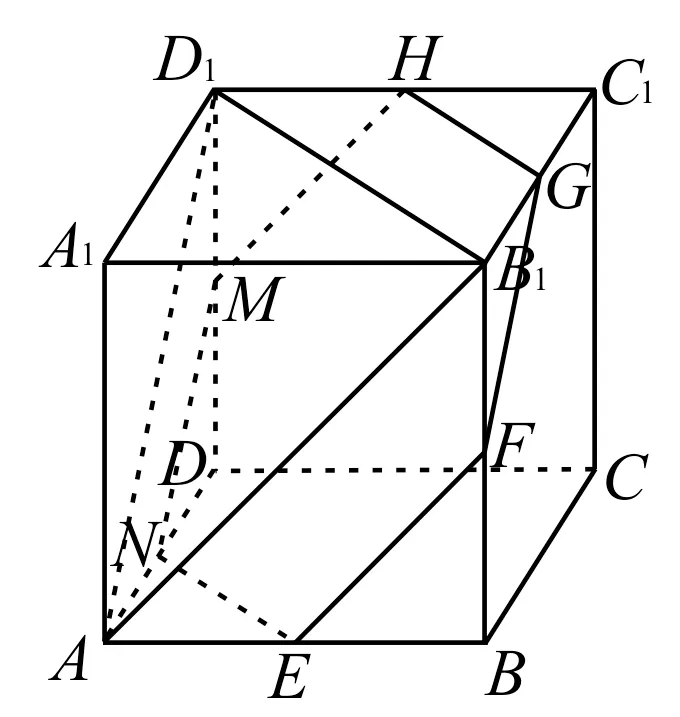
图10
A.3 4 3 B.2 3 3
C.3 4 2 D.23
提示:在正方体ABCD-A1B1C1D1中,平面AB1D1与棱A1A,A1B1,A1D1所成的角都相等。因为正方体的其余棱都分别与A1A,A1B1,A1D1平行,所以正方体ABCDA1B1C1D1的每条棱所在的直线与平面AB1D1所成的角都相等。
取棱AB,BB1,B1C1,C1D1,D1D,DA的中点分别为E,F,G,H,M,N,则正六边形EFGHMN所在平面与平面AB1D1平行且面积最大,此截面面积为S正六边形EFGHMN=。应选A。

