液体悬浮式非能动停堆组件落棒分析程序的试验验证

袁浩然，匡波，刘鹏飞，王欣，黎闫

1. 上海交通大学 核科学与工程学院，上海 200240

2. 中国原子能科学研究院，北京 102413

快堆超设计基准事故分析表明：在失电或主冷却泵故障停转同时伴随主停堆系统失效时，为了防止堆芯过热，有必要采用一套辅助停堆系统。因此，除了主停堆系统之外，可以补充引入一套非能动停堆装置，作为提高快堆固有安全性的措施之一。非能动安全特征从提出到现在出现了多种设计方案[1]，其中液体悬浮式非能动停堆装置，是在发生假想的无保护瞬态发生的失流事故（unprotected loss of flow，ULOF）时[2]，依靠该停堆装置组件随堆芯流量下降导致其水力−动力特性的变化，而实现非能动地落棒停堆装置。这一装置因其具有卡棒概率小，很好地非能动应对ULOF事故能力等特点，成为一种颇具吸引力的方案[3]。国外对液体悬浮式非能动停堆装置的研究较早[4]，国内对其技术正在进行设计试验研究[5]。

1 非能动停堆组件水力−动力学分析

1.1 原理

典型的液体悬浮式非能动停堆装置组件及其在不同堆芯流量下的悬停与下落状态如图1所示。装置中液体悬浮棒（移动体，内装中子吸收体）在足够大流量冲刷下悬停于堆芯上方（图1(a)）；一旦发生失流，堆芯惰转流量降至一定临界流量时，移动体所受水力推力不再能够使移动体悬停从而发生落棒，其中吸收体逐渐进入堆芯内（图1(b)），直至移动体完全插入下位（图1(c)）。针对该液体悬浮式停堆装置，设计要求在实际ULOF事故堆芯流量降至预定临界值时，组件移动体能够非能动地落棒进入堆芯；根据反应堆安全运行需求，移动体的落棒曲线与落棒时间均要满足一定要求[6]。

图1 组件示意

1.2 组件移动体动力学分析

非能动停堆组件移动体在各种工况液钠流量的作用下，不仅受重力Fg，还受阿基米德浮力Fb、水力推力FD（实质上是由流体与移动体固壁相对运动时所受水力阻力压降引起）作用，合力大小与方向决定了移动体动力学特性与运动状态。此外，当处于上、下工作位（刚性位）时，移动体还受来自驱动机构或下管座（及其他静止部分）的支撑力FM作用，以平衡其他各力，使移动体静止停留于上、下工作位。如图1所示。非能动停堆组件移动体运动状况可通过下面的动力学方程描述：

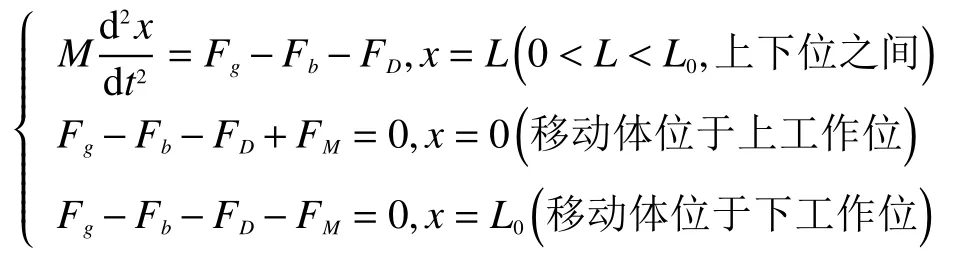
式中：M为移动体质量，kg；x为移动体位移，m，上、下工作位分别有 x=0、L0；t为时间，s；Fg=Mg是移动体所受重力，N；Fb=ρVg为移动体所受浮力，N，其中ρ为液体的密度，kg/m3，V为移动体排开液体体积，m3；FM为移动体在上、下工作位时所受静止部分支撑力，N；FD为移动体所受水力推力，N。

1.3 组件水力学析

1.3.1 非能动组件流网模型

移动体所受到的水力推力FD的计算是研究其运动特性的关键。而水力推力取决于非能动组件的流道结构及流道内的水力学特性。在堆芯流量冲刷下的停堆组件流道是由组件内外件（移动体与外套管）共同围成的内、外流道构成，其中有彼此连通的各形式子流道及其组合，形如直管、棒束、环缝、折管、分岔管、小孔、锥面等，由此形成复杂的流体网络。流体流过组成的元件及其组合将形成沿程与局部的压降；同时这些沿程与局部阻力压降也取决于流经各元件及组合的液钠流量 Q 以及子流道内的流量分配（Q1，Q2，Q3，…）。可基于流体网络理论来分析组件内阻力与流量分配。结合流网节点流量流入与流出量守恒与并联管路支路阻力损失相等的关系，可得到流网控制方程：

式中Qi、ΔP分别是各元件流道内流量及元件端节点间压降。基于上述流体网络模型即可求解非能动组件内各子流道元件内的流量分配。

1.3.2 非能动停堆组件的水力推力

非能动停堆组件所受水力推力FD的计算式可写为

根据典型移动体设计，局部阻力元件分解为截面突缩/突扩、三通分流、三通汇流、直角转弯等基本元件（如图2所示）；主要沿程阻力元件有长直圆管、棒束流道以及环管等基本元件（如图3所示）。

图2 典型局部阻力元件

图3 典型沿程阻力元件

对于各沿程及局部阻力元件的压降计算，一般地采用下面统一的形式[7]：

式中沿程及局部阻力系数可参考文献[8]选取。

同时，考虑到在实际组件流道结构中会受以下两方面因素影响：1）各沿程阻力元件尺寸较小，且流动可能受未充分发展等非理想因素影响；2）在部分相邻的局部阻力元件之间，由于受上一个局部阻力影响而致流体连续绕流，彼此靠近元件间可能存在局部阻力相邻影响[9]。为此，本文在典型元件结构尺寸与流量范围内，通过水力试验台架的一系列元件及元件组合压降的实测对比，对上述沿程阻力元件以及相邻局部阻力元件组合的沿程/局部阻力压降系数进行修正。此外，考虑计算失流条件下的堆芯流量动态变化（流量惰转），还需基于流体动力学分析，进一步考虑流量动态变化影响并进行相应的非定常流量修正。主要结果如下：

1)考虑未充分发展流等非理想因素的影响，沿程阻力元件的修正

沿程阻力压降系数的修正结果如表1所示。

其中D为环管外径，m；δ为内管与外管间隙，m；Φ为棒束直径，m。

表1 沿程阻力修正

2)考虑元件间相邻影响等非理想因素的影响，局部阻力元件的修正[10]可参照

局部阻力元件压降相邻影响因素等的修正结果如表2所示。其中d为节流孔直径，m。

表2 元件组合局部阻力的相邻影响修正

在计算各子流道阻力压降时，由于移动体运动过程（上升、悬停以及下落）会带来移动体与外套管间的相对运动，从而使构成整个流网的子流道发生变化（流道重组）；此外，在计算非能动组件与外套管间环缝的沿程压降时，考虑到组件移动体下落使流体与组件表面相对速度增加，此处对相对速度修正，即

3)对于非能动组件入口流量变化的情况（如流量惰转），可由纳维−斯托克斯方程推导获得，计算水力推力时还需增加一个非定常修正项[11]：

2 组件水力−动力学特性分析程序

基于上述流网模型与阻力压降计算方法，对流道结构、流量分配及水力推力的时空分布采用准稳分布加瞬态修正的方式，在此基础上对非能动停堆组件移动体动力学方程式(1)、(2)进行时−空离散求解，从而综合分析非能动停堆组件的水力学特性与落棒运动等动力学行为。结合耦合求解流网方程、移动体动力学方程、非能动停堆组件水力−动力学特性数学模型，开发了计算程序PSSD，程序计算流程如图4所示。

图4 PSSD 计算流程

需要说明，在PSSD程序中，为提高计算效率，水力学流网方程与移动体动力学方程的耦合求解在时层上采用显式耦合方式，在实际程序计算时需进行时层网格敏感性计算，确定计算的最大时间步长；同时，PSSD程序中考虑流网方程组及移动体动力学方程的非线性，采用了牛顿迭代法进行求解。

3 失流惰转工况条件下组件落棒试验与分析程序验证

3.1 试验装置与试验段

为了验证组件水力−动力学特性及程序的适宜性，本文针对某一典型设计的组件，进行了特定惰转流量条件下的落棒模拟试验，验证试验在如图5所示的水力试验回路上进行。试验段流道及组件模拟体相对于原型流道及组件按几何比为1:1设计。采用去离子水作为试验介质，模拟堆内液钠流动；为保证试验时模型流动与原型流动的水力相似，试验中保证水介质黏性与密度跟堆内条件下约360 ℃的液钠相当（即保证模型与原型Re数相等），为此试验水温控制在约84 ℃，试验系统压力控制在150 kPa左右（试验系统通过氮气加压，防止试验时水流通过流道阻力件时因压降而发生闪蒸）；同时试验中模拟流量及其变化与实堆流量相等。

图5 水力试验回路

试验段采用全尺寸组件，全尺寸组件高度为7 m，移动体下落位移为1 m；非能动停堆组件安装在全高度垂直试验本体中（图6所示）。首先用抓持机构将移动体提至上工作位；其次使回路中达到额定流量与压力（模拟快堆非能动组件实际工作环境）；最后松开抓持机构释放，移动体处于上工作位悬停状态。

图6 非能动停堆组件试验段

为了得到准确的落棒特性，采用高速摄影拍摄落棒过程。在移动体上画上标尺线（如图7所示），用来作为移动体的定位特征。进而计算得到移动体下落位置、速度等物理量。

图7 落棒可视化试验装置

3.2 落棒试验与可视化测量

试验时通过连续调节通过本体流道的流量，以模拟实堆惰转流量变化。图8给出了预设惰转流量与实际惰转流量变化曲线（其中采用YOKOGAWA质量流量计，流量测量不确定度为 5.1×10−3kg/s）。由图8可以看到，实测的试验惰转流量曲线与预计的惰转流量曲线较好地符合，说明试验流量的调节能够较好模拟实际惰转流量的变化，满足试验要求。

图8 预设与实际调节的惰转流量

在惰转流量下的落棒模拟试验过程中，当试验流量降至某一临界流量值时，移动体开始下落（落棒）。本文试验中采用高速摄影通过可视化观测窗，进行非能动棒模拟件的落棒运动观测。采用motion pro Y3高速摄影仪，可视化拍摄速度采用 125 f/s，分辨率为 1 280×1 024。

运用图像二值化质心定位处理技术得到二值图像质心，计算如下：

然后记录质心横纵坐标于矩阵中，在背景图中显示质心。此时经过处理的有限帧图像中，关键目标质心提取图显示如图9（白色正方形为标记质心）。

图9 移动体质心处理图像

最后对通过对相邻2帧图像质心位置进行提取，可得到1/125 s内移动体运动的距离，将每2帧非能动棒运动数据进行统计，可得到其整个下落运动过程的位移−时间图像。

考虑测量精度以及可视化图像像素、拍摄速度精度、移动体的横向位移等其他因素的影响，经综合估算，本试验中非能动棒位移测量不确定度估计为 0.21 mm。

3.3 落棒试验结果与程序验证

按照设定的试验工况与图8所示的惰转流量曲线进行多次试验，得到的落棒位移曲线与相应的PSSD程序计算结果相对比，多次试验的最大偏差值在设计偏差的范围之内（设计要求5%）。如图10所示为某次试验结果。从图中可以看到，落棒曲线的预测结果与实测结果符合较好，计算落棒时间与实测值偏差约 0.48 s（计算 13.16 s，试验12.68 s），由此初步验证试验落棒曲线与PSSD计算曲线较为符合。通过试验证明，PSSD程序可有效地应用于非能动停堆组件的水力学设计，以及实际落棒过程的分析计算。

图10 落棒曲线的预测与实测值对比

4 结论

本文建立快堆液体悬浮式非能动停堆组件落棒计算程序，修正了程序的计算模型并进行了落棒试验验证得到如下结论：

1）程序计算的落棒曲线与实测符合较好，由此验证了所开发的非能动停堆组件落棒计算模型与程序的适宜性；

2）通过程序的修正与试验验证，为液体悬浮式非能动停堆组件的设计提供理论计算模型；

3）建议进一步优化程序计算模型，提高理论计算的准确性。