公钥密码体制中大整数分解算法研究

王兴波 唐春明 李建辉

摘  要：通过对文献资料的归类分析，结合大整数分解理论和实践的具体发展，从宏观层面将大整数分解的历程划分为四个阶段并归纳出了每个阶段的基本特征，同时结合国内研究情况总结出了国内研究的特点，指出了国内外研究的差别以及国内研究的某些局限性。文章最后还介绍了最近几年新发现的基于二叉树研究方法的特色及其取得的成果，展示了一些算例并揭示了未来的相关研究方向和内容。文章可作为研究大整数分解算法的参考。

关键词：计算数论;密码学;整数分解;算法

中图分类号：TN918      文献标识码：A 文章编号：2096-4706（2020）16-0125-09

Study on Algorithms of Big Integer Factorization in Public-key Cryptosystem

WANG Xingbo1，TANG Chunming2，LI Jianhui3

（1.Foshan University，Foshan  528225，China;2.Guangzhou University，Guangzhou  510006，China;

3.Foshan Polytechnic，Foshan  528137，China）

Abstract：Based on the classification and analysis of literature，combined with the specific development of the theory and practice of large integer decomposition，the process of large integer decomposition is divided into four stages from the macro level，and the basic characteristics of each stage are summarized. At the same time，the characteristics of domestic research are summarized based on the domestic research situation，and the differences between domestic and foreign research and some limitations of domestic research are pointed out. At the end of the paper，the characteristics and achievements of the new research method based on binary tree in recent years are introduced，and some examples are presented，and the related research directions and contents in the future are revealed. This paper can be used as a reference for studying large integer factorization algorithm.

Keywords：computational number theory;cryptography;integer factorization;algorithm

0  引  言

大整數分解问题是数论的困难问题之一，也是人类尚未完全解决的科学问题之一，一直受到世界各国众多数学和信息安全工作者的关注。近百年来，人类对于破解这个难题的努力一直未有间断，其间有兴奋、失落，亦有努力和希望并行，构成了解决这个难题的艰难历程。

近50年来，学者们主要在大整数分解基础理论方法与分解实践两方面开展研究。分解理论主要在寻找高效的分解算法方面，而分解实践则主要集中在RSA实验室1991年公布的系列RSA模数及数论里悬疑的一些特殊数如梅森数、费马数等。

1975年到1995年近20年的时间，大整数分解理论从技术层面产生了一些优秀的算法，如Pollard Rho算法、连分数法（Continued fraction，CFRAC）、二次筛法（Quadratic Sieve，QS）、平方型分解法（SQUare FOrm Factorization，SQUFOF）、椭圆曲线法（ECM）和数域筛法（Number Field Sieve，NFS）等。1996年12月美国数学协会通讯（NOTICES OF THE AMS）发表了一篇题为《两个筛法的故事》（“A Tale of Two Sieves”）的长文。作者Carl Pomerance是二次筛法的创始人，通过该文介绍了当时理论与实践的各种成就，成功与期盼之情跃然纸上。然而自该文后25年过去了，大整数分解的问题依然没有解决。

笔者早在上大学之时就对这个问题充满憧憬，还给数学大师陈景润写信，信誓旦旦地要解决这个问题。后来参加研究生复试时，导师说：“这个问题留待你退休后研究吧！”时至今日，退休之日近在咫尺，回想几十年对这个问题的了解和研究，模仿Carl Pomerance讲故事的方式，向读者回顾近30年来人类辛苦探索该问题的历程，同时也介绍笔者及其团队对这个问题的研究结果。

1  国内外研究概况

高效分解整数的算法无疑是解决大整数分解难题的关键。近50年来，国内外都有学者在不停地耕耘，其间也取得了令人欣慰的成就，从技术层面产生了很多优秀的算法。很多文献已经对这些算法的技术特点、理论价值做了介绍，故本文在这里不再赘述。本文主要关注大整数分解的发展历程和每个时期的特点，从宏观层面总结这个辛酸与期望并存的求索过程。

1.1  国外研究

根据国内外的文献综述情况，国外对于整数分解的研究成果可分为四个阶段：

（1）无“计”可施阶段：持续数百年的试除法和Fermat方法;

（2）“众说纷纭”阶段：1975年前后到1995年前后20年左右;

（3）“计穷力竭”阶段：1995年到2010年前后15年左右;

（4）“再入迷茫”階段：2010年至今。

以下分别简述各阶段的主要成果及特点。

1.1.1  1975年以前“无计可施”的数百年

历史上人类对于整数分解的问题除了试除（试除法）以外，可谓无“计”可施，直到17世纪业余数学家Pierre de Fermat提出了Fermat法以后才算有一个基本解决方法。试除法和Fermat法在所有因数分解的教科书里都有介绍。它们直观易懂，分解大整数的效率很低，适合分解小整数，是1970年以前分解整数的主要方法。对于分解大整数而言，这两个方法都“无计可施”。文献[1]将此称为“束手无策”（参见文献[1]第19页）。

1.1.2  1975年—1995年“众说纷纭”的20年

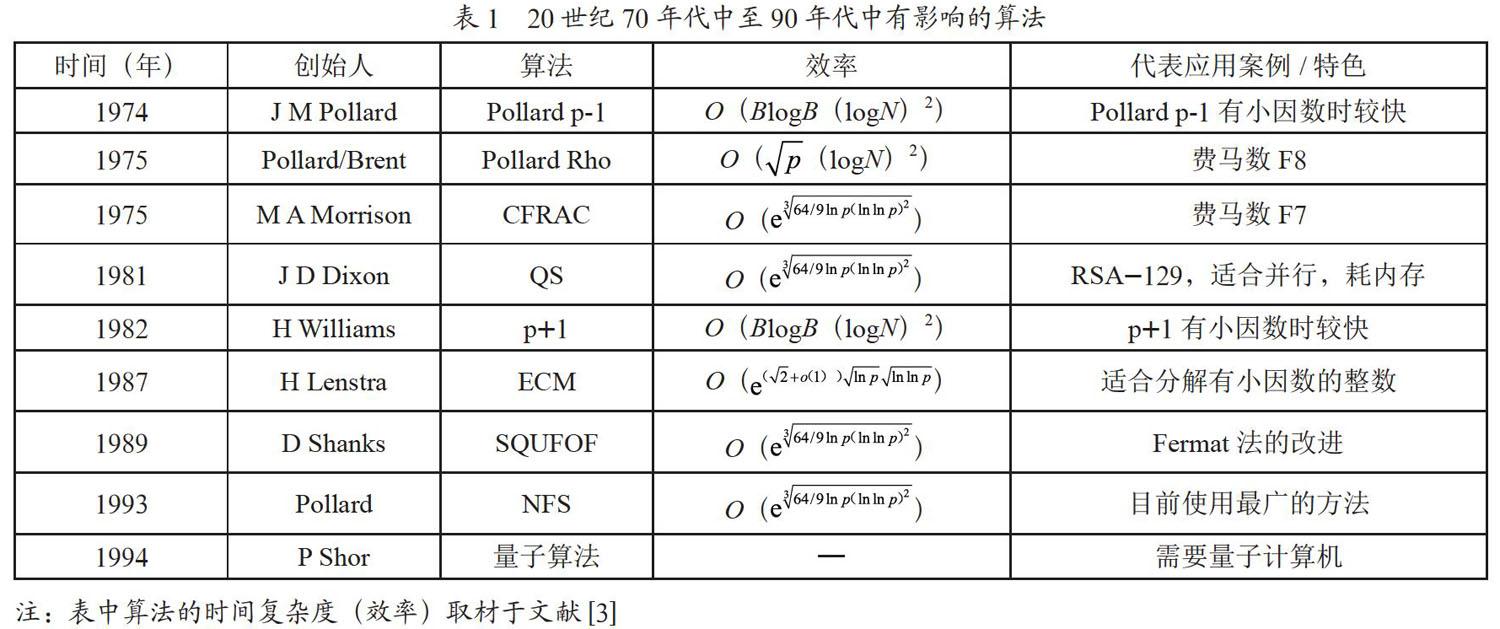
国内外文献记录和相关综述表明[1-6]，20世纪70年代中至90年代中是人类研究整数分解的高峰时期，也是相关成果出现的密集期，堪称整数分解算法研究的“众说纷纭”时代。综合各种综述文献，可发现这个阶段产生了各有所长的10多种分解算法。表1列举了一些有影响的算法。

1.1.3  1995年—2010年“计穷力竭”的15年

1974年后密集出现的各种算法，让数学家对解决分解整数的难题充满了希望。各种先进计算机的研制成功，甚至让一些人认为分解大整数已经不是什么问题了。但是RSA实验室向世人展示了一个严酷的事实——大整数分解依然困难。1991年3月，RSA实验室公布了一组RSA模数并为每个模数设置了奖金——分解了所公布任何模数都能获得对应的奖金。由此开辟了应用与检验当时各种分解算法的阶段，并且分解RSA模数成为计算数论与密码学界检验分解算法成效的标志性指标。

随着高性能计算机的问世，并行计算自然成为研究和采用的基本手段。各种算法的并行化是该阶段的研究特征。1990年，Brent R P就研究了整数分解并行计算的可能性。在文献[7]中，Brent指出Pollard Rho算法在并行计算时效率并没有明显提高，认为该算法的并行计算意义不大;他同时指出ECM和QS的并行计算效果较好。1999年，Brent总结了当时的并行计算成果并发表了文献[8]。2000年Wolski E的团队给出了ECM的并行计算法[9];同年，Brynielsson J发表了二次筛法的并行计算方法[10]。2005年—2007年，Mcmath S S及其团队先后发表了二次型法与连分数法的并行计算特征[11，12]。随后几年，如文献[13][14]所述，NFS并行化得到广泛关注并取得了不菲成就。到目前为止，NFS被认为是效率最高的分解算法。从表2所列已分解的RSA模数及其分解方法可知，几乎每个被分解的模数都能用NFS分解。

NFS在分解RSA模数方面的成功运用似乎抑制了人们继续挖掘更好算法的欲望。相比1975年—1995年的20年期间产生了近10种算法，在1995年—2010年的15年期间，没有比NFS更有影响力的算法出现。目前，并行NFS在分解大的RSA模数方面几乎是不二的选项。正因为如此，笔者称这个时期是“计穷力竭”阶段。

1.1.4  2010年以来“再入迷茫”的年代

从前面2小节的历史陈述可以看出，到目前为止所有常规算法（串行或并行）在分解具有小因数的整数方面都很成功，但是在分解大整数方面仍然不尽人意。人们不得不面临一个残酷的现实问题：效率最高的NFS需要通过并行计算系统或超级计算机耗费巨量计算资源来实现[15]。例如，著名的RSA-768就是基于80个2.2 GHz AMD皓龙（Opteron）四核心CPU的并行计算历经半年得到分解的[16]。Bruce Schneier于2019年12月分解RSA-240时用了800个物理核做筛子外加100个物理核做矩阵。文献[17]统计，NFS分解768位（二进制）目标时，因子基需要240 MB内存、筛子需要10 GB、矩阵计算需要160 GB，分解1 024位目标则分别需要7.5 GB、256 GB和10 TB的内存。目前只有拥有大计算资源的国家和地区，才有条件开展相应的研究[18]。正因为如此，有网友戏谑预测：在天河二号上跑半年也许能够分解RSA-232。事实上，Bruce Schneier在分解RSA-240时，采用Intel Xeon Gold 6130 CPU共花了4 000核年的计算量，折算在天河二号上，大概需要1 000个天河节点及24 000个天河计算核，持续运行300天（费用开销估算在1 728万元人民币左右）。

鉴于这样的现实，印度学者近年来开展了较为活跃的研究，如文献[19]到文献[23]，得到了  甚至  级别确定性时间复杂度的算法，但这些算法对于大整数而言仍然意味着冗长的计算。也有印度学者进行Fermat方法优化、甚至有人将离散优化的粒子算法引入到整数分解计算（相关文献在researchgate可查，部分处在preprint状态故未列入文献清单），但总体来说印度学者仍未展示系统性解决方案的成果。有学者试图在GPU上实施RSA模数分解[24];但据笔者与该文作者本人的交流，他的研究没有取得实质性的进展，仅仅是一个设想、发表了一篇论文而已。有部分其它学者在2003年—2008年间也做过有条件的确定性时间复杂度分解RSA数的算法研究，如文献[25]、[26]，但正如文献[6]所陈述的，这些算法的效率低于随机化算法的效率，且这些研究均未见实证结果。

截至目前为止，RSA公布的待分解模数中，尚有RSA-232、RSA-250、RSA-260、RSA-896、RSA-1024、RSA-1536、RSA-2048等多个未被分解。笔者认为，除非有新的革命性算法，否则大整数分解依然是继续挑战人类智力极限的一个数学难题。

1.2  国内研究

国内对于整数分解的研究由来已久，例如《九章算术》就记录了很多整数分解的例子，这些例子展示的方法比国外要早很多年。但是遗憾的是，在现代研究方面，国内主要以借鉴国外方法为主，鲜有超越国外的独立研究报道。

笔者分别以“整数分解”“大数分解”“RSA分解”“整数+因子+分解”“整数+因数+分解”及“RSA攻击”为关键词，在CNKI检索1991年1月至2020年1月的文献情况如表3所示。

经筛选，真正与分解算法研究相关的文献按照时间先后顺序排列见文献[1]、[3]、[5]及文献[27]到文献[54]，涉及的研究内容如表4所示。

基于表3、表4的数据，笔者总结出“综述学习”“局部探索”和“顶天不立地”三个特征来描述。

1.2.1  综述学习

该类主要集中在硕、博士研究生群体的研究，也有知名学者的启蒙教育，成果多以学位论文或教材等读物表现，特点是综述国外的方法，从中获取一定的知识，比如文献[1]、[3]、[5]、[32]、[40]、[46]及[48]都属于这样的研究。

文献[1]属于教材式文献，原本是写给中学生的读物，但文中综述了相关方法的进展，是非常不错的启蒙读物。

文献[3]、[5]属于综述型文献，回顾了当时主流的大数因子分解算法，介绍了这些算法的基本原理和实现步骤，对比分析了现有大数因子分解技术在实现和应用上的优缺点并展望了大整数分解未来的研究趋势。

文献[32]综述了各种大整数因子分解算法，讨论了QS和NFS的优化问题。

文献[40]通过对已有的因子分解算法的分析、总结、比较，提出了一个新的因子分解算法和一个因子分解方法的新研究方向。但是根据笔者对所提方法的剖析，发现该方法采用了类似试除法的搜索过程，其效率并不高。

文献[46]考察了中国古代数学中所蕴含的整除理论、探究了西方数学中的数论起源、考察了素数基本理论、探讨了整数分解的几种经典算法、论述了密码学发展的三个阶段：古典密码、近代密码和现代密码。笔者认为，该文仍处在启蒙阶段。

文献[48]属于一般转抄、拼凑型综述。

1.2.2  局部探索

該类研究基于相关的数学理论与计算机算法，针对RSA算法的特征，进行了局部问题的建设性研究或者探索性研究，如文献[29]、[31]、[34]、[35]、[36]、[37]、[42]、[43]、[44]、[45]、[49]及[54]均属于此类。

文献[29]在分解大整数小因子算法的基础上，提出的优化分解树算法，利用树型数据结构和相应的构造算法与回溯算法，配合以作者提出的分解表截支方法和优化分组策略，可以将分解大整数小因子的速度提高50%以上，但该文无数据对比，且构造树本身需要时间。笔者认为此法还有待挖掘。

文献[31]对一大类大整数的因子分解构造了分解算法，通过求解模数的小因数来实现分解，其本质是特殊Pollard p-1方法。

文献[34]阐述了大数分解法二次筛选法优化，提出了参数、硬件等多个优化方案，但缺少实施的措施，属于一般性描述。

文献[35]介绍了详细阐述了大数分解法QS以及它的改进算法MPQS和PPMPQS的理论基础。文中宣称设计了一种快速寻找PP关系的方法并利用VC6实现了PPMPQS，成功分解了十进制70位的大数，但文中未见分解实例。事实上，单纯利用VC6而不借用大数运算工具包，如gmp大数库、NTL大数库或者MIRAC大数库，是很难表示70位十进制大数的。

文献[36]证明了：若丢番图方程ax+by=z（（a，b）=1）的整数解（x0，y0，z0）满足x0=O（log2ab），y0=O（log2ab）且

z0=O（log2ab）;那么存在一个多项式时间的算法分解n=ab并时间不超过 。该文是笔者所看过国内文献中较有参考价值的一个。但考虑到从丢番图方程的解集中寻找符合分解因子的过程也需要时间，其算法效率未免要打折扣。事实上，利用笔者的方法仅搜索了4步就分解了该文所述案例，计算时间仅数毫秒。

文献[37]对试除法进行了改进，减少试除次数提高了试除法运算效率，在算法上并无新的创意。

文献[42]提出了一种整数分解的判定算法，本质是将计算中间过程中的素数判定去除，仍然属于改进Fermat算法的类别，其计算效率为O（plogN），低于Pollard Rho的效率。

文献[43]提出了一种用于求解大整数因数分解问题的尾数多相位粒子群搜索算法MMPPSO。但数值实验表明该文大多数算例的结果是错误的，少数正确的结果中还有与文献[36]中的算例雷同的。

文献[44]根据RSA数的特性及Euclid算法的特点，给出了一种析出分解算法，并进行了算法的数学证明和相关分析。笔者发现，该算法的效率与Fermat法相当，也存在需要完善的地方。

文献[45]是一篇博士论文，从理论上探讨了构造一类椭圆曲线，就该类椭圆曲线的非扭有理点x-坐标与曲线方程系数D的分解进行研究，并尝试将有理数域上椭圆曲线分解整数的方法推广到虚二次域K上，涉及较深奥的椭圆曲线知识。鉴于笔者对此方面不甚了解，不敢贸然评价，但显而易见的是该文最后没有给出具体解决方案。

文献[49]将分解整数因子的费马法迭代过程分为两个阶段，采用合适的算法加快平方和开方运算，避免无效运算，使总体计算量大大减少。该文没有与其他方法进行比较，难以确定其提高效率的有效性。

文献[54]通过变换随机序列产生式，对Pollard Rho算法在计算离散对数方面进行了改进，提高Pollard Rho算法的效率。考虑到离散对数计算与整数分解之间的本质关系[55]，鉴于Pollard Rho算法对于大整数分解的局限性，笔者认为对于大整数分解，还需配合它法。

1.2.3  顶天不立地

该类研究的特点是接触非常规计算技术的时代前沿，提出一个时期时尚的概念和一段时间难以验证的方法，如文献[28]、[33]、[38]、[39]、[30]、[41]、[50]、[51]、[52]及[47]属于此类。

文献[28]、[33]、[38]给出整数分解的并行或分布式计算实现原理，但未见具体计算方案，此后至今未见后续的相关报道。其实分布式计算取决于对解空间的划分，如比特币的挖矿算法，网格计算等。小规模（几台或几十台计算机）有可能，大规模异构分布式并行计算本身就是一个复杂的研究课题。

文献[39]提出了Pollard p-1因子分解的DNA计算机算法，以Pollard p-1算法为基础，利用DNA分子生物操作完成加，减，乘，除运算，实现平方-乘以及欧几里德算法，其本质是对欧几里德运算中的算术运算进行变换，在分解方法上面，没有实质性的发展。该文也没有具体有说服力的算例。

文献[30]、[41]、[50]、[51]、[52]给出新的量子算法。但到目前为止，国内尚无法验证，国际上也缺乏所需验证条件。人们可以从科学的角度去研究未来的科学产出，但是大整数分解是与信息安全密切相关、科学与工程一体的科学技术共生体，既需要顶天的科学理论又需要立地的务实技术才能解决问题。

文献[52]试图实施Pollard p-1因子分解的DNA计算机算法，未见具体计算方案，也未见后续成果报道。

文献[47]提出云计算的设想，没有对大整数运算的环境作分析，也未见后续报道。其实基于云计算分解整数仅仅是网格计算的延伸，跟分布式并行计算一样，需要很细致的策划和方案乃至每个结点实现的算法，包括云上计算环境的配置等，需要细致的方案和措施。

1.3  国内外研究对比及目前辛酸的局面

通过前面几小节对国内外算法研究及实践现状的总结，不难得到如下结论：

（1）国外学者侧重于提出系统的解决方案，尤其上世纪70年代中至90年代中产生了系列的解决方案，在整数分解方面取得了实质性的成就;

（2）国内主要以吸收国外研究为特征，到目前為止整数分解理论和方法都基本没有产生超越国外水平的成果报道;

（3）在经典计算机体系结构下，NFS是目前应用最广的方法。在量子计算机结构下，量子算法是人们的希望所在。尽管如此，1995年以来，国内外在分解大整数这一数学难题的方法学上，没有超越NFS和量子算法的成果报道。由于量子算法受制于量子计算机的发展，NFS是目前在分解实践中的主要方法;

（4）大整数分解至今仍然是挑战人类智能水平的一个世界难题，等待人类的解决。

2  二叉树上的数论展现了新的希望

赋值二叉树是王兴波教授研究奇数时采用的一种方法[56]。该方法将大于1的奇数（注：后文所述奇数均指大于1的奇数）从上到下从左到右置于一棵二叉树上来研究，揭示了奇数许多鲜为人知的性质。例如子树根的因数与后代之间存在近亲回避律（若干层内一定没有根的倍数出现），子树之间存在复制传递性以及子树的根与后代结点的公因数存在对称律等等[57-60]。最为重要的是，它揭示了奇数的遗传特质——在以奇数N为根的子树中，N都以一种仅与其自身相关的递归方式分布在其子孙结点的因数中，并且可以通过基因结构、基因图与余基因图等由奇数N的倍数组成的数据结构来描述[61]。基因图与余基因图形成一幅遗传图谱，可演绎出整数分解的新方法。

2.1  奇数的遗传图谱

奇数的遗传特质可用图1直观地说明。取以3为根的子树T3为例：T3第三层首末两个结点9、15具有因数3，以9、15为根的子树在其第三层的首末两个结点也含有因数3，此规律一直在T3中延续。以5为根的子树T5在其第四层第2个和倒数第2个结点具有因数5，这种规律在T5中延续。更有意思的是，以15为根的子树T15，分别继承了T3和T5的前述属性，在其第三层首末结点包含因数3、在第四层第2个和倒数第2个结点具有因数5，且这种规律在T15中延续。

记TN表示以大于1的奇数N为根的赋值二叉树。文献[56][61]证明了，TN中存在一个N的遗传结构g（N）（genetic structure），也存在一个由N的倍数组成的基因图G（N）（genetic graph）和余基因图G*（N）（complementary genetic graph）。若p是N的一个因数，G（p）与G*（p）是p的基因图与余基因图。G（N）与G*（N）合起来称为N的遗传图谱或基因图谱（genetic atlas），它也是TN的一棵子树。

2.2  遗传图谱与整数分解

奇数的遗传图谱对于整数分解具有重要意义，它能提供整数分解的一种新途径。文献[61]证明了：当N是含有因数p的奇合数时，TN上同层两个G（N）结点之间一定存在G（p）或G*（p）的结点。这就意味着，一旦得到了G（N），就能在其上找到G（p）或G*（p）的结点。由于G（p）和G*（p）的结点都是p的倍数，因此p是这些结点与N之间的公约数。从而N的分解可以转化为寻找在G（N）或G*（N）上寻找G（p）或G*（p）的结点。

设N=pq，1

2.3  取得的成果

基于前述二叉树上奇数的遗传特征，近几年的研究取得了以下研究成果。

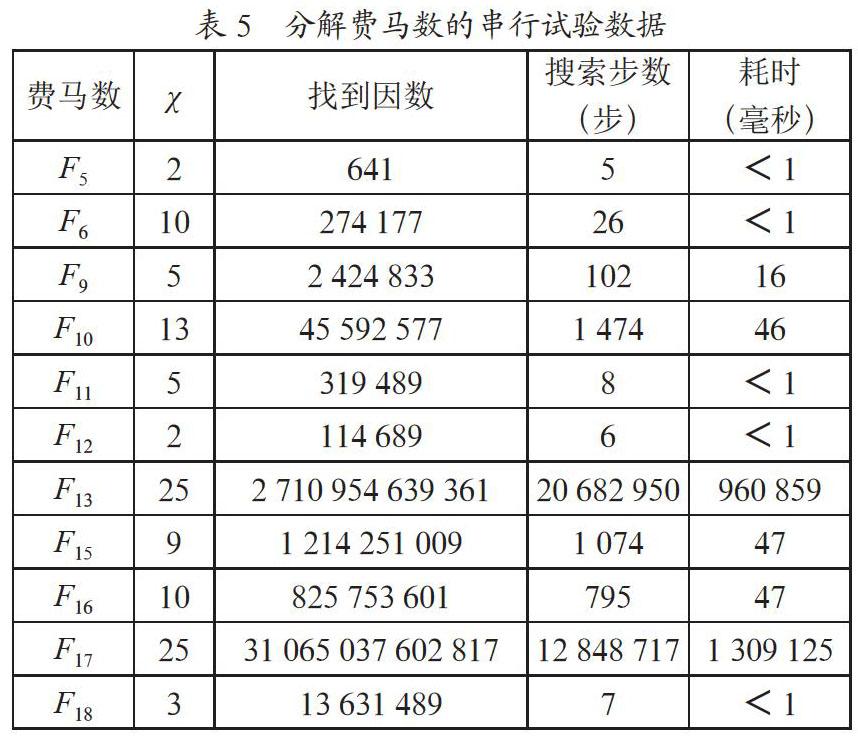
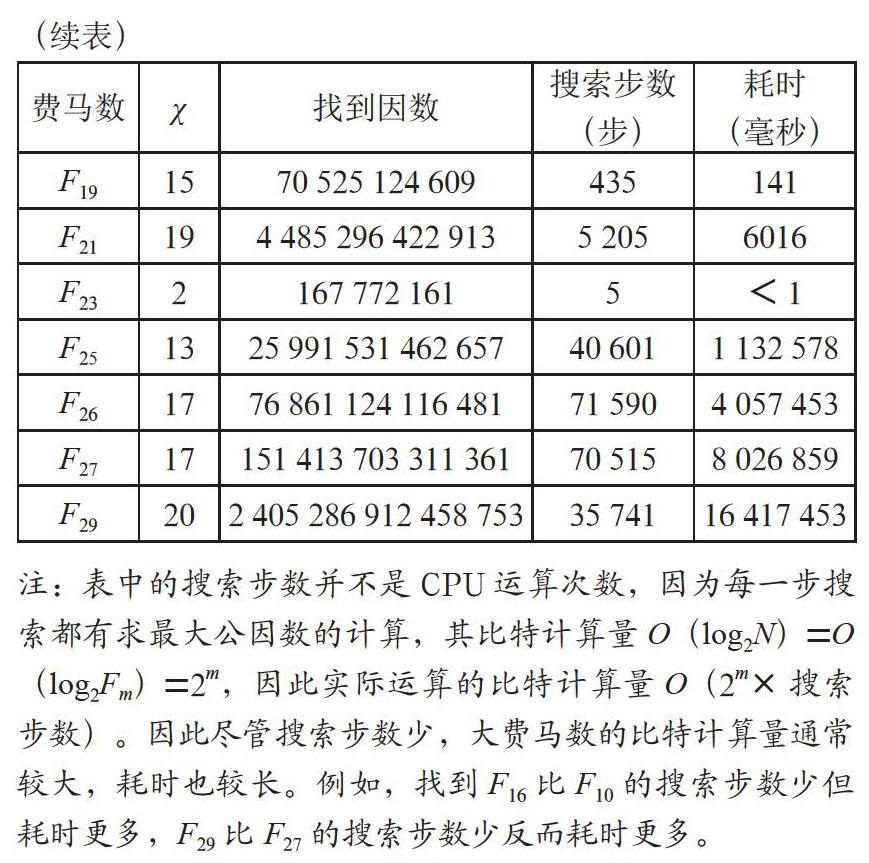
2018年，分别找到了殆素数因数比对其小因数分布的影响关系[62]。李建辉教授据此设计了并行分解算法并成功分解了46位十进制殆素数[63]。试验表明，在串行模式下分解22位以内的十进制合数时明显优于Pollard Rho方法。与目前广泛应用的数域筛法（NFS）或GNFS相比，新的算法占用极少内存。2018年还研究了T3树上结点与其平方根的关系[64]以及RSA模数的因数分布特征[65]。

2019年1月，证明了奇数的因子具有呈周期性分布在树的边界和围栏上的规律，并藉此用新的方法再次演绎证明了p+1分解法[66]。如图3所示，树TN的边界是树上最左结点或最右结点组成的，而树的围栏则是由如 、 所示紧靠边界的奇数组成的。

2019年年初还找到RSA模数的平方根与因数之间的分布规律[67]以及RSA模数在T3树上的分布规律[68]。证明了：RSA模数N的两个因数中或者处在T3树的同一层、或者处在相邻两层，其中一定有一个与  裹挟在同一层。

2019年4月证明了整数乘积的长度与因数长度的关系，特别证明了：因数比小于2的RSA模数之两个因数都是等长的[69]。

2019年5月，藉由前述研究结果，证明了：若整数N= pq的两个因子满足1

2020年1月，证明了：若整数N=pq的两个因子满足q=2αu±1，1

2020年5月，证明了：若整数N=pq的两个因子满足1

结合德国Wilfrid Keller教授对u的估值范围[72]，如有合适的大费马数计算工具，每个大费马数Fm（m>100 001）能在普通计算机上瞬间分解。读者可向王兴波教授索取Maple源程序进行测试。

2.4  未来研究

遗传特征主要是根结点在其子孙结点之间的因数传递规律。两棵不同的子树之间也存在传递规律，称之为过渡（transition）。研究发现，这个过渡可通过在两棵子树之间建立联络（connection）来完成。例如图4中的65可以通过25计算出来。但是25不是T5的结点而属于另外一棵树的结点（注意：这不是通过观察得知而是根据文献[61]推论8的结论演绎的）。

树的域外的结点属于另外一棵子树，因此联络也是树际间结点的关系的描述，其解析计算关系无疑是树际间因数倍数传递的最直接表现，也是整个整数遗传图谱结构中不可忽视的关系。例如N=pq可视N是Tp树与Tq树的联络转换点。最近研究发现，在Tp树与Tq树里分别存在一个X与Y，在TN树里面有一个m满足m=qX=pY，如图5所示。显然，通过m找到X或Y的任何一个，就能找到p或者q了，其计算的时间复杂度都是对数级的。树际间的联络关系，不仅是子树之间的连接纽带，而且可能提供分解整数的一般法则。目前，笔者及团队正在努力研究出新的结果。

在树上一层寻找某个目标结点是一个与搜索有关的问题。事实上，整数分解算法大都表现为在某些集合里面寻找一些特定目标。比如，Pollard Rho算法本质上是一种随机化搜索算法。每个算法针对的潜在目标集合不同，导致搜索效率各异。前期研究所发现可将殆素数的因数定位于某个区间内的结果，最后也只有设计出有效的搜索算法才能实现分解。通过判断某特征数是否在某区间[73]、将目标区间进行有效分划以便实现随机化算法设计和并行计算[74]、采用区间树方式减少搜索量[75，76]等研究，发现树上树上搜索与各种进化算法（智能算法）关系密切，或许是一粒开门的“芝麻”。目前，笔者和团队也在进行相关的探索。

3  结  论

大整数的分解是一个历史难题，也是一个现实的难题。人类对这个难题的研究和探索是一个充满辛酸与希望的，面向晨曦在泥泞中跋涉的历程。相对于国外学者提出的种种系统性解决方案，国内研究尚需要在系统性和原创性方面努力。笔者和团队近年来基于二叉树开展的整数研究新方法，有望成为一个原创性可系统解决整数分解问题的研究方法。笔者希望广大读者通过本文的介绍，能够了解、理解和认同探索者们的努力与付出，加入到这个艰难的研究活动中，一起变梦想为现实。

参考文献：

[1] 颜松远.整数分解 [M].北京：科学出版社，2009.

[2] SURHONE L M，TENNOE M T，HENSSONOW S F. RSA [M].Beau Bassin：Betascript Publishing，2013.

[3] 董青，吴楠.整数质因子分解算法新进展与传统密码学面临的挑战 [J].计算机科学，2008（8）：17-20.

[4] SARNAIK S，GADEKAR D，GAIKWAD U. An Overview to Integer Factorization and RSA in Cryptography [J].International Journal For Advance Research In Engineering And Technology，2014，2（9）：21-27.

[5] 劉新星，邹潇湘，谭建龙.大数因子分解算法综述 [J].计算机应用研究，2014，31（11）：3201-3207.

[6] WANAMBISI A W，AYWA S，MAENDE C，et al. Factorization of Large Composite Integer [J].International Journal of Mathematics and Statistics Studies，2013，1（1）：39-44.

[7] BRENT R P. Vector and parallel algorithms for integer factorization [C]//Proc Third Australian Supercomputer Conference.1990.

[8] BRENT R P. Some Parallel Algorithms for Integer Factorisation [C]//Euro-Par99 Parallel Processing. Heidelberg：Springer，1990： 1-22.

[9] WOLSKI E，FILHO J G S，DANTAS M A R. Parallel Implementation of Elliptic Curve Method for Integer Factorization Using Message-Passing Interface （MPI） [EB/OL].（2017-02-18）http：//www.lbd.dcc.ufmg.br/colecoes/sbac-pad/2001/007.pdf

[10] ?SBRINK O，BRYNIELSSON J. Factoring large integers using parallel Quadratic Sieve [EB/OL].（2000-04-14）.http：//citeseerx.ist.psu.edu/viewdoc/summary？doi=10.1.1.96.3685.

[11] MCMATH S S. Parallel Integer Factorization Using Quadratic Forms：U.S.N.A-trident Scholar Project Report：No.339 [R/OL].（2005-05-09）.http：//cadigweb.ew.usna.edu/～wdj/mcmath/.

[12] MCMATH S S，CRABBE F，JOYNER D. Continued fractions and Parallel SQUFOF [J].International Journal of Pure and Applied Mathematics，2007，34（1）：19-38.

[13] YANG L T，XU L，LIN M. Integer Factorization by a Parallel GNFS Algorithm for Public Key Cryptosystems [C]//Embedded Software and Systems，ICESS 2005.Heidelberg：Springer，2005：683-695.

[14] DAOUD S，GAD I. A parallel line sieve for the GNFS Algorithm [J].International Journal of Advanced Computer Science and Applications，2014，5（7）：178-185.

[15] YEH Y S，HUANG T Y，LIN H Y，et al. A Study on Parallel RSA Factorization [J].Journal of Computers，2009，4（2）：112-118.

[16] AOKI K. Advances in Integer Factoring Technique——The Way to Factor RSA-768 [J].IPSJ Magazine，2010，51（8）：1030-1038.

[17] SONALKER A A. Asymmetric Key Distribution [D].Raleigh：North Carolina State University，2002.

[18] WANG Q，FAN X B，ZANG H Y，et al. The Space Complexity Analysis in the General Number Field Sieve Integer Factorization [J].Theoretical Computer Science，2016，630：76-94.

[19] COSTA E，HARVEY D. Faster deterministic integer factorization [J].Mathematics of Computation，2014，83（285）：339-345.

[20] CARELLA N A. Deterministic Integer Factorization Algorithms [J/OL].arXiv：1308.2891 [cs.DS].（2013-08-05）.https：//arxiv.org/abs/1308.2891.

[21] SHIPILEVSKY Y. Polynomial Time Integer Factorization [J/OL].viXra：1407.0063.（2014-07-08）.https：//vixra.org/abs/1407.0063.

[22] HIARY G A. A deterministic algorithm for integer factorization [J].Mathematics of Computation，2015，85（300）：2065-2069.

[23] HITTMEIR M. A babystep-giantstep method for faster deterministic integer factorization [J]. Mathematics of Computation，2018，87（314）：2915-2935.

[24] LIN C H，LIU J C，LI C C，et al. Parallel Modulus Operations in RSA Encryption by CPU/GPU Hybrid Computation [C]//2014 Ninth Asia Joint Conference on Information Security.Wuhan：IEEE，2015：71-75.

[25] ABOUD S J，ABU-TAIEH E M. A new deterministic RSA-factoring algorithm [J].Journal of Apply Science.2006，8（1）：54-66.

[26] CORON J S，MAY A. Deterministic Polynomial-Time Equivalence of Computing the RSA Secret Key and Factoring [J].Journal of Cryptology，2007，20（1）：39-50.

[27] 隆永红.用L～3算法分解RSA的模 [J].湘潭大学自然科学学报，1993，15（3）：128-132.

[28] 蒋增荣，曾泳泓，成礼智.大整数分解算法及其并行实现 [J].中山大学学报论丛，1996（5）：6-12.

[29] 崔竞松，彭蓉，张焕国，等.一种快速分解大整数的小因子的优化分解树OFT算法 [J].计算机学报，2003，26（11）：1435-1440.

[30] 霍红卫，潘征.大数质因子分解的量子算法 [J].计算机工程与科学，2003，25（1）：23-25+41.

[31] 王泽辉.大整数因子分解新算法及对RSA密码制的解密 [J].中山大学学报（自然科学版），2003，42（5）：15-18.

[32] 戴阔斌.大整数因子分解问题的研究 [D].湖北：武汉大学，2004.

[33] 李栋，邹衡，王佐.一种新的基于分布式的RSA模数分解算法 [J].现代情报，2005（4）：220-221+223.

[34] 戴阔斌，陈建华.大整数因子分解中的二次筛法优化 [J].數学杂志，2005，25（6）：659-663.

[35] 褚一平，陈勤.分解RSA模数算法研究 [J].微机发展，2005（6）：91-92+160.

[36] ZHANG S H，CHEN G L，QIN Z P，et al. An Method of Factoring Large Integers [J].信息安全与通信保密，2005（7）：108-109.

[37] 伍传敏，孟金涛，刘俊芳.两类整数分解算法的分析与改进 [J].计算机工程与设计，2007，28（17）：4094-4095+4104.

[38] 李骏.分布式计算环境下大整数分解的研究 [D].上海：上海交通大学，2007.

[39] 王静，李肯立，许进.Pollard p-1因子分解的DNA计算机算法 [J].计算机研究与发展，2008，45（Sl）：67-71.

[40] 陈笑伟.关于大数分解问题的研究 [D].西宁：青海师范大学，2009.

[41] 付向群，鲍皖苏，周淳.Shor整数分解量子算法的加速实现 [J].科学通报，2010，55（Z1）：322-327.

[42] 孙克泉.RSA密码分析中分解大整数的判定算法 [J].计算机工程，2010，36（15）：142-144.

[43] 张淑梅，宋维堂，宋万里.一种用于大整数因数分解的多相位粒子群算法 [J].计算机工程与应用，2010，46（25）：105-108.

[44] 孙克泉.分解大整数为两个素因子乘积的析出算法 [J].天津职业院校联合学报，2011，13（8）：37-42.

[45] 李修美.数域上的椭圆曲线与整数分解 [D].北京：清华大学，2013.

[46] 杨莉莉.大数分解的若干历史问题研究 [D].临汾：山西师范大学，2014.

[47] 刘倩，范安东，许凌云，等.云计算在RSA密码体制分析中的应用 [J].数学的实践与认识，2014，44（3）：108-114.

[48] 楊晨鹤，王周宁馨，张祯.关于大整数分解的方法探究 [J].科技资讯，2015，13（7）：243-244.

[49] 徐明毅.整数因子分解的费马法改进 [J].洛阳师范学院学报，2016，35（8）：1-5.

[50] 王亚辉，颜松远.一种新的攻击RSA的量子算法 [J].计算机科学，2016，43（4）：24-27.

[51] 王亚辉，张焕国，吴万青，等.基于方程求解与相位估计攻击RSA的量子算法 [J].计算机学报，2017，40（12）：2688-2699.

[52] 王平平，陆正福，杨春尧，等.Shor量子算法的分析及优化 [J].通信技术，2017，50（4）：775-778.

[53] 杨江帅.大整数分解算法综述 [J].信息技术与网络安全，2018，37（11）：12-15.

[54] 胡建军，王伟，李恒杰.Pollard ρ算法改进 [J].计算机应用研究，2018，35（7）：2153-2155.

[55] 樱井幸一，陈治中.密码·数论·计算理论的未解决问题 [J].数学译林，2002，21（3）：198-204.

[56] WANG X B. Valuated Binary Tree：A New Approach in Study of Integers [J].International Journal of Scientific and Innovative Mathematical Research，2016，4（3）：63-67.

[57] WANG X B. Amusing Properties of Odd Numbers Derived From Valuated Binary Tree [J].IOSR Journal of Mathematics，2016，12（6）：53-57.

[58] WANG X B. Two More Symmetric Properties of Odd Numbers [J].IOSR Journal of Mathematics，2017，13（3）：37-40.

[59] WANG X B. Some More New Properties of Consecutive Odd Numbers [J].Journal of Mathematics Research，2017，9（5）：61-70.

[60] WANG X B. T3 Tree and Its Traits in Understanding Integers [J].Advances in Pure Mathematics，2018，8（5）：494-507.

[61] WANG X B. Genetic Traits of Odd Numbers With Applications in Factorization of Integers [J]. Global Journal of Pure and Applied Mathematics，2017，13（2）：493-517.

[62] WANG X B. Influence of Divisor-ratio to Distribution of Semiprimes Divisor [J].Journal of Mathematics Research，2018，10（4）：54-61.

[63] LI J H. A Parallel Probabilistic Approach to Factorize a Semiprime [J].American Journal of Computational Mathematics，2018，8（2）：175-183.

[64] WANG X B. More on Square and Square Root of a Node on T3 Tree [J].International Journal of Mathematics and Statistics Study，2018，6（3）：1-7.

[65] WANG X B，SHEN Z. Traits of a RSA Modulus on T3 Tree [J].Journal of Mathematics Research，2018，10（6）：15-29.

[66] WANG X B，GUO H Q. Some Divisibility Traits on Valuated Binary Trees [J].International Journal of Applied Physics and Mathematics，2019，9（1）：1-15.

[67] WANG X B，MIAO Y J. Relationship between Divisors Distribution and Square Root of a RSA Modulus [J].International Journal of Information and Electronics Engineering，2019，9（1）：7-11.

[68] WANG X B，GUO H Q. Distribution of RSA Numbers Divisor on T3 Tree [J].International Journal of Information and Electronics Engineering，2019，9（1）：23-29.

[69] WANG X B. Number of Digits in Two Integers and Their Multiplication [J].Journal of Advances in Applied Mathematics，2019，4（2）：69-74.

[70] WANG X B，ZHONG J J. Fast Approach to Factorize Odd Integers with Special Divisors [J].Journal of Mathematics and Statistics，2020，16（1）：24-34.

[71] WANG X B. Algorithm Available for Factoring Big Fermat Numbers [J].Journal of Software，2020，15（3）：86-97.

[72] WILFRID K. Prime factors k·2n+1 of Fermat numbers Fm and complete factoring status [EB/OL].（2020-07-01）.http：//www.prothsearch.com/fermat.html.

[73] WANG X B. Two Number-guessing Problems Plus Applications in Cryptography [J].International Journal of Network Security，2019，21（3）：494-500.

[74] WANG X B，GUO J X. Deterministic-Embedded Monte Carlo Approach to Find out an Objective Item in a Large Number of Data Sets [J].International Journal of Applied Physics and Mathematics，2019，9（4）：173-181.

[75] WANG X B. Interval Tree and Its Application in Integer Factorization [J].Journal of Mathematics Research，2019，11（2）：103-113.

[76] WANG X B，WU J C. Traits of Interval Tree in Solving Blind Search Problems of Finding a Term in an Ordered Data Set [J].International Journal of Information and Education Technoloy，2020，10（7）：516-522.

作者简介：王兴波（1963—），男，汉族，湖北安陆人，教授，工学博士，主要研究方向：先进制造与计算机应用相关的教学科研工作;通讯作者：李建辉（1974—），男，汉族，湖南岳阳人，教授，博士，研究方向：信息安全、多重分形和網络优化。