一类分数阶q-导数方程非平凡解的存在性

郭福日，张 英

(山西大同大学数学与统计学院，山西大同037009）

许多年来，人们对分数阶边值问题的研究始终没有间断过，究其原因，一方面是由于分数阶方程理论的进一步完善，另一面是分数阶方程在许多领域得到了广泛的应用。特别是关于分数阶q-导数方程的研究掀起了一股热潮，见文献[1-8]上，上述文献大部分讨论的是分数阶q-导数方程正解的存在唯一性，利用的方法主要是不动点理论。文献[4]利用单调迭代方法，讨论了非线性分数阶微分方程边值问题

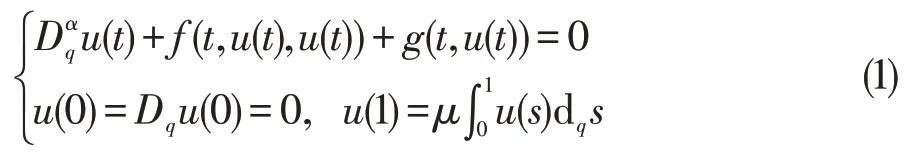
正解的存在唯一性。讨论下面分数阶q-导数积分边值问题

非平凡解的存在性，其中2 ＜α≤3，0 ＜μ＜[α]q。

定义符号如下：

若b=0 时，a(α)=aα。

定义q-伽马函数为：

并且有Γq(x+1)=[x]qΓq(x)。

函数f的q-导数为：

(Dq f)(x)=且(Dq f)(0)=(Dq f)(x)。

函数f的高阶q-导数：

函数f的q-积分为：对每一个x∈[0,b],

函数f的高阶q-积分：

利用微分算子Dq与积分算子Iq关系可知：

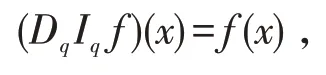
并且当函数f(x)在x=0 连续时有

定义1函数f：[0,1]→R的α(α＞0)阶q-积分Riemann-Liouville 型为(Iαqf)(x)=f(s)dqs。

定义2函数f：[0,1]→R的α(α＞0)阶q-导数为

给出4个关于积分与导数的公式

(IV)sDq(t-s)(α)=-[α]q(t-qs)(α-1)。

引理1假设α＞0，p∈N，则下面等式成立

证明对任意的α＞0，(I)首先证明当p=1时，由于

因此我们得到：

即当p=1时等式成立；

(II)假设当p=N时成立 (其中N为正整数)，p=N+1时也成立。

证明

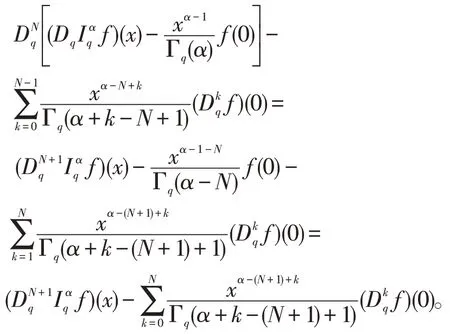
即引理得证。

引理2假设B为巴拿赫空间，C是一个锥且C⊂B。若Ω1,Ω2为B中的开集，且0 ∈ Ω1，⊂ Ω2，假设T：C∩Ω1)→C为全连续算子，使得‖Ty‖≥‖y‖,y∈C∩ ∂Ω1且‖Ty‖≤‖y‖，y∈C∩ ∂Ω2。那么算子T至少有一个不动点在C∩Ω1)[9]。

引理3设2＜α≤3 ，0 ＜μ＜[α]q，x∈C1[0,1]，则下列边值问题

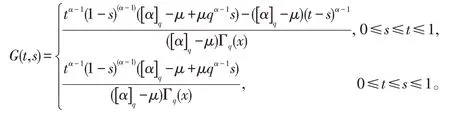
引理4格林函数G(t,s),t,s∈[0,1]具有下面的性质：

(I)G(t,qs) 是连续函数，并且G(t,qs)≥0，t,s∈[0,1]；证明见文献[6]；

(II)G(t,qs)≤G(qs,qs),t,s∈[0,1]。这里只证明(II)：令

则

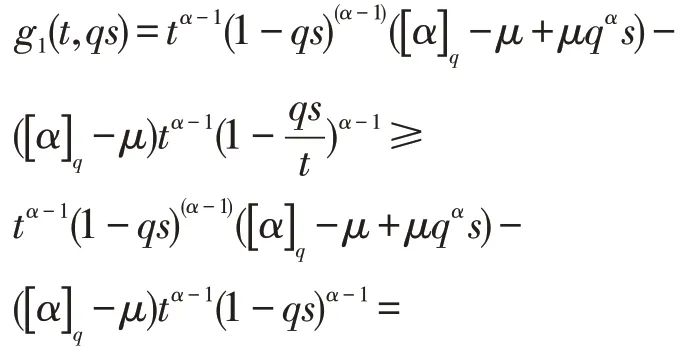
tα-1(1-s)(α-1)μqαs ≥ 0。

很容易得到

又因为

这表明g1(t,s) 关于变量t单调递减的，对每一个s∈(0,1]。因此，g1(t,qs)≤g1(qs,qs)，s,t∈(0,1]。很显然，g2(t,s) 关于t单调递增，因此我们可以得到G(t,qs)≤G(qs,qs)，s,t∈(0,1]。

我们定义两个常数

定理1假设f(t,u)：[0,1]×[0,∞)→(0,+∞)为连续函数。如果存在两个正数r2＞r1＞0 使得

成立，那么问题(2)有一个解y(t)满足r1≤‖y‖≤r2。

证明令B=C[0,1]，取 范数 ‖u‖=supt∈[0,1]|u(t)|，定义锥P⊂B且P={u∈B：u(t)≥ 0}。

给定算子：(Tu)(x)利用G和f的非负性及连续性可知，T(P)⊂P且T为全连续算子。从而定理1的证明等价于算子方程Ty=y有解，而且解满足r1≤‖y‖ ≤r2。

利用G(t,qs)≤G(qs,qs)及f(t,u)≥L2r1，可得

利用G(t,qs)≤G(qs,qs)及f(t,u)≤L1r2，可得

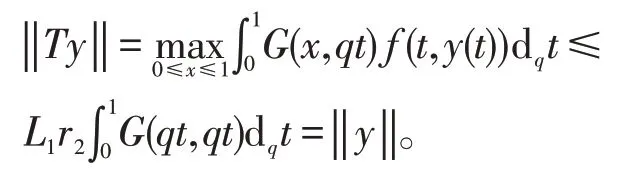
由引理2 可知方程(2)有至少有一个解y，而且满足r1≤‖y‖ ≤r2，从而定理得证。